目录
[2.1 红黑树的概念](#2.1 红黑树的概念)
[2.2 红黑树的性质](#2.2 红黑树的性质)
[3.1 节点定义](#3.1 节点定义)
[4.1 插入步骤](#4.1 插入步骤)
[4.2 插入代码实现](#4.2 插入代码实现)
[5.1 验证步骤](#5.1 验证步骤)
[5.2 验证代码实现](#5.2 验证代码实现)
[6.1 迭代器的定义](#6.1 迭代器的定义)
[6.2 迭代器的递增和递减操作](#6.2 迭代器的递增和递减操作)
[七、红黑树模拟实现 map 与 set](#七、红黑树模拟实现 map 与 set)
[7.1 set 的模拟实现](#7.1 set 的模拟实现)
[7.2 map 的模拟实现](#7.2 map 的模拟实现)
一、引言
在数据结构的世界里,平衡二叉搜索树是高效组织和查询数据的重要工具。红黑树作为平衡二叉搜索树的一种,因其良好的平衡特性和相对简单的实现,在许多场景中得到广泛应用,尤其是在C++ 的标准模板库(STL)中, map 和 set 等关联式容器的底层实现就依赖于红黑树。本文将深入探讨红黑树的原理、实现细节,并结合代码详细展示其在模拟 map 和 set 容器中的应用。
二、红黑树的概念与性质
2.1 红黑树的概念
红黑树是一种二叉搜索树,在每个节点上增加了一个存储位来表示节点的颜色,颜色可以是红色(Red)或黑色(Black)。通过对从根到叶子的路径上各个节点着色方式的限制,红黑树确保没有一条路径会比其他路径长出两倍,从而达到近似平衡的状态。
2.2 红黑树的性质
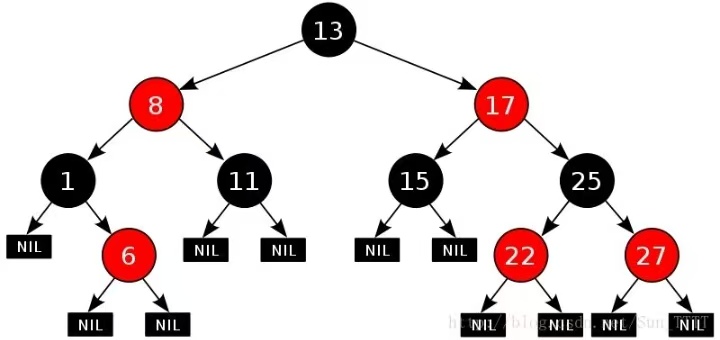
节点颜色性质:每个节点不是红色就是黑色。
根节点性质:根节点是黑色的。
红色节点性质:如果一个节点是红色的,则它的两个孩子节点是黑色的。
黑色节点高度性质:对于每个节点,从该节点到其所有后代叶节点的简单路径上,均包含相同数目的黑色节点。
叶子节点性质:每个叶子节点(此处的叶子节点指的是空节点)都是黑色的。
这些性质保证了红黑树的最长路径不会超过最短路径的两倍,使得树的高度相对平衡,从而在插入、删除和查找操作上都能保持高效。
三、红黑树的节点定义与结构
3.1 节点定义
在C++ 中,我们可以如下定义红黑树的节点:
cpp
cpp
// 节点的颜色
enum Color {RED, BLACK};
// 红黑树节点的定义
template<class ValueType>
struct RBTreeNode
{
RBTreeNode(const ValueType& data = ValueType(), Color color = RED)
: _pLeft(nullptr), _pRight(nullptr), _pParent(nullptr)
, _data(data), _color(color)
{}
RBTreeNode<ValueType>* _pLeft; // 节点的左孩子
RBTreeNode<ValueType>* _pRight; // 节点的右孩子
RBTreeNode<ValueType>* _pParent; // 节点的双亲(红黑树需要旋转,为了实现简单给出该字段)
ValueType _data; // 节点的值域
Color _color; // 节点的颜色
};
这里将节点的默认颜色设为红色,主要是为了在插入新节点时,尽量减少对树结构调整的次数。因为插入红色节点比插入黑色节点更不容易破坏红黑树的性质,后续可以通过旋转和变色操作来恢复性质。3.2 红黑树结构
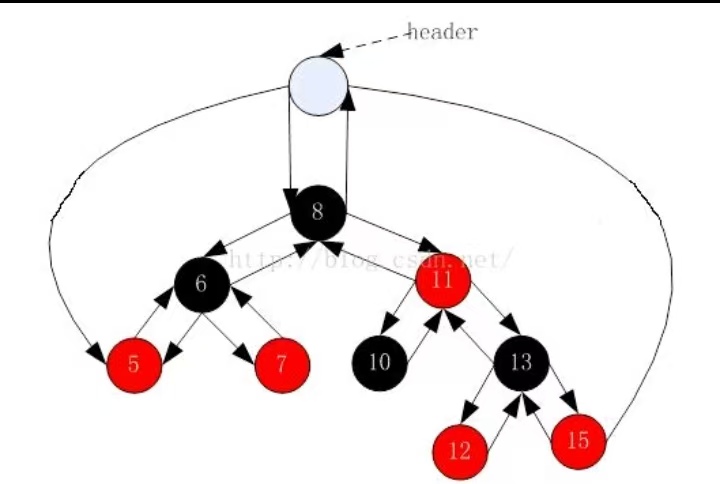
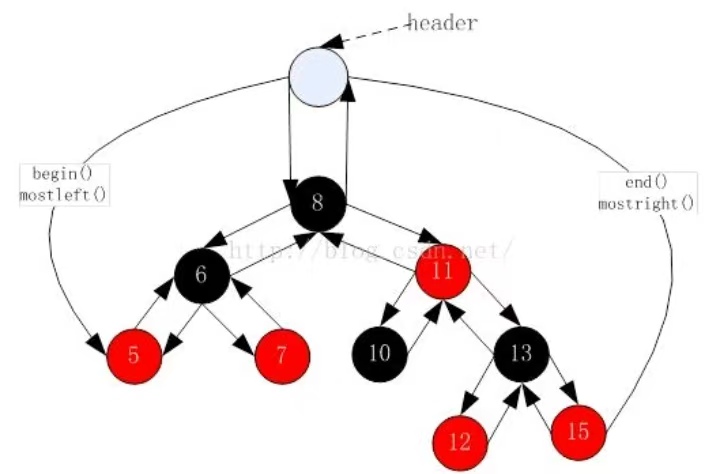
为了方便实现关联式容器,我们在红黑树的实现中增加一个头结点。头结点颜色为黑色,其 _pParent 域指向红黑树的根节点, _pLeft 域指向红黑树中最小的节点, _pRight 域指向红黑树中最大的节点。以下是红黑树类的基本框架:
cpp
cpp
template<class K, class ValueType, class KeyOfValue>
class RBTree
{
typedef RBTreeNode<ValueType> Node;
typedef Node* PNode;
public:
typedef RBTreeIterator<ValueType, ValueType*, ValueType&> Iterator;
RBTree();
~RBTree();
// 迭代器相关
Iterator Begin() { return Iterator(_pHead->_pLeft); }
Iterator End() { return Iterator(_pHead); }
// 插入操作
pair<Iterator, bool> Insert(const ValueType& data);
// 清空树
void Clear();
// 查找操作
Iterator Find(const K& key);
// 容量相关
size_t Size() const;
bool Empty() const;
private:
PNode _pHead;
size_t _size; // 红黑树中有效节点的个数
};四、红黑树的插入操作
4.1 插入步骤
红黑树的插入操作分为两步:
按照二叉搜索树规则插入新节点:从根节点开始,根据新节点值与当前节点值的大小比较,向左或向右遍历树,直到找到合适的插入位置,插入新节点。新插入节点默认颜色为红色。
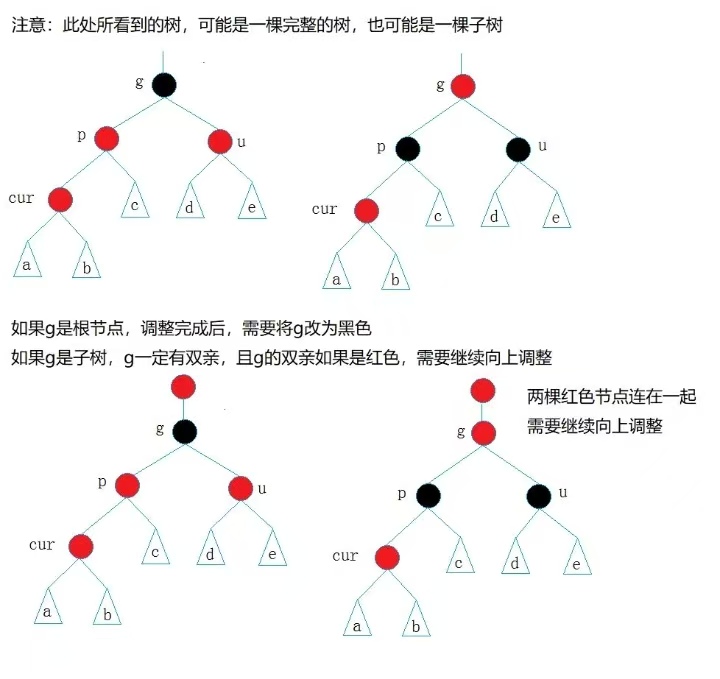
检测并修复红黑树性质:由于新插入节点为红色,可能会违反红黑树的性质(主要是性质3:不能有连在一起的红色节点),此时需要对树进行调整,通过旋转和变色操作来恢复红黑树的性质。
4.2 插入代码实现
cpp
cpp
template<class K, class ValueType, class KeyOfValue>
pair<typename RBTree<K, ValueType, KeyOfValue>::Iterator, bool>
RBTree<K, ValueType, KeyOfValue>::Insert(const ValueType& data)
{
PNode& pRoot = _pHead->_pParent;
if (nullptr == pRoot)
{
pRoot = new Node(data, BLACK);
pRoot->_pParent = _pHead;
_pHead->_pLeft = _pHead->_pRight = pRoot;
_size++;
return make_pair(Iterator(pRoot), true);
}
KeyOfValue kofv;
PNode pCur = pRoot;
PNode pParent = nullptr;
while (pCur)
{
if (kofv(pCur->_data) > kofv(data))
{
pParent = pCur;
pCur = pCur->_pLeft;
}
else if (kofv(pCur->_data) < kofv(data))
{
pParent = pCur;
pCur = pCur->_pRight;
}
else
{
return make_pair(Iterator(pCur), false);
}
}
pCur = new Node(data);
pCur->_pParent = pParent;
if (kofv(pParent->_data) > kofv(data))
{
pParent->_pLeft = pCur;
if (_pHead->_pLeft == _pHead)
{
_pHead->_pLeft = pCur;
}
}
else
{
pParent->_pRight = pCur;
if (_pHead->_pRight == _pHead)
{
_pHead->_pRight = pCur;
}
}
_size++;
// 检测并修复红黑树性质
while (pParent && pParent->_color == RED)
{
PNode grandFather = pParent->_pParent;
if (pParent == grandFather->_pLeft)
{
PNode uncle = grandFather->_pRight;
// 情况一:叔叔节点存在且为红
if (uncle && uncle->_color == RED)
{
pParent->_color = BLACK;
uncle->_color = BLACK;
grandFather->_color = RED;
pCur = grandFather;
pParent = pCur->_pParent;
}
else
{
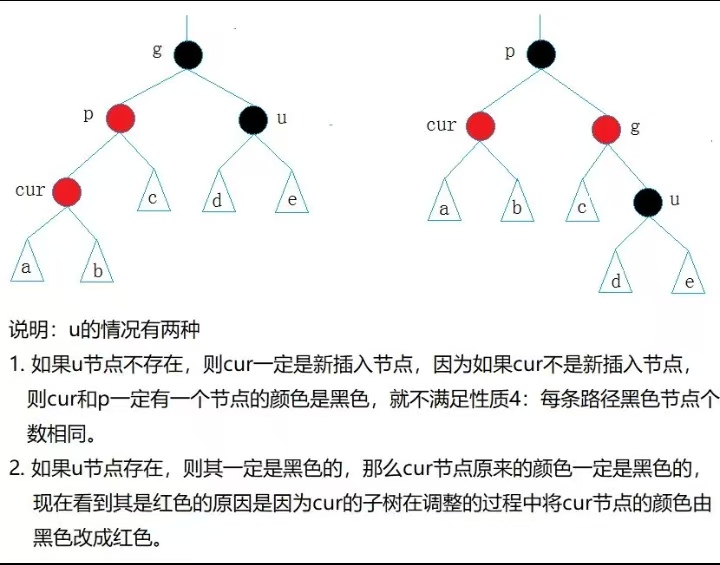
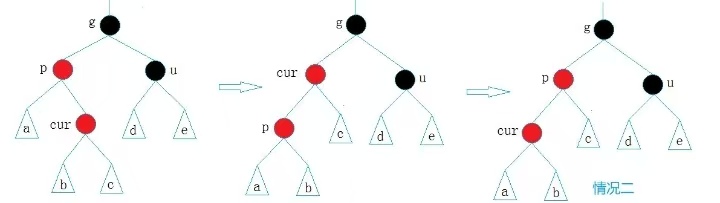
// 情况二:叔叔节点不存在或为黑
if (pCur == pParent->_pRight)
{
_RotateLeft(pParent);
swap(pParent, pCur);
}
pParent->_color = BLACK;
grandFather->_color = RED;
_RotateRight(grandFather);
}
}
else
{
PNode uncle = grandFather->_pLeft;
if (uncle && uncle->_color == RED)
{
pParent->_color = BLACK;
uncle->_color = BLACK;
grandFather->_color = RED;
pCur = grandFather;
pParent = pCur->_pParent;
}
else
{
if (pCur == pParent->_pLeft)
{
_RotateRight(pParent);
swap(pParent, pCur);
}
pParent->_color = BLACK;
grandFather->_color = RED;
_RotateLeft(grandFather);
}
}
}
_pHead->_pParent->_color = BLACK;
return make_pair(Iterator(pCur), true);
}上述代码中, _RotateLeft 和 _RotateRight 分别是左旋和右旋操作的函数,实现如下:
cpp
cpp
template<class K, class ValueType, class KeyOfValue>
void RBTree<K, ValueType, KeyOfValue>::_RotateLeft(PNode pParent)
{
PNode pSubR = pParent->_pRight;
PNode pSubRL = pSubR->_pLeft;
pParent->_pRight = pSubRL;
if (pSubRL)
{
pSubRL->_pParent = pParent;
}
pSubR->_pLeft = pParent;
PNode pPParent = pParent->_pParent;
pParent->_pParent = pSubR;
if (pPParent == nullptr)
{
_pHead->_pParent = pSubR;
}
else if (pPParent->_pLeft == pParent)
{
pPParent->_pLeft = pSubR;
}
else
{
pPParent->_pRight = pSubR;
}
pSubR->_pParent = pPParent;
}
template<class K, class ValueType, class KeyOfValue>
void RBTree<K, ValueType, KeyOfValue>::_RotateRight(PNode pParent)
{
PNode pSubL = pParent->_pLeft;
PNode pSubLR = pSubL->_pRight;
pParent->_pLeft = pSubLR;
if (pSubLR)
{
pSubLR->_pParent = pParent;
}
pSubL->_pRight = pParent;
PNode pPParent = pParent->_pParent;
pParent->_pParent = pSubL;
if (pPParent == nullptr)
{
_pHead->_pParent = pSubL;
}
else if (pPParent->_pLeft == pParent)
{
pPParent->_pLeft = pSubL;
}
else
{
pPParent->_pRight = pSubL;
}
pSubL->_pParent = pPParent;
}
五、红黑树的验证
5.1 验证步骤
红黑树的检测分为两步:
检测是否满足二叉搜索树性质:通过中序遍历,检查遍历结果是否为有序序列。
检测是否满足红黑树性质:检查根节点是否为黑色,以及每条路径上黑色节点的个数是否相同等性质。
5.2 验证代码实现
cpp
cpp
template<class K, class ValueType, class KeyOfValue>
bool RBTree<K, ValueType, KeyOfValue>::IsValidRBTree()
{
PNode pRoot = _pHead->_pParent;
// 空树也是红黑树
if (nullptr == pRoot)
{
return true;
}
// 检测根节点是否为黑色
if (pRoot->_color!= BLACK)
{
std::cout << "违反红黑树性质二:根节点必须为黑色" << std::endl;
return false;
}
// 获取任意一条路径中黑色节点的个数
size_t blackCount = 0;
PNode pCur = pRoot;
while (pCur)
{
if (pCur->_color == BLACK)
{
blackCount++;
}
pCur = pCur->_pLeft;
}
// 检测是否满足红黑树的性质,k用来记录路径中黑色节点的个数
size_t k = 0;
return _IsValidRBTree(pRoot, k, blackCount);
}
template<class K, class ValueType, class KeyOfValue>
bool RBTree<K, ValueType, KeyOfValue>::_IsValidRBTree(PNode pRoot, size_t k, const size_t blackCount)
{
// 走到null之后,判断k和black是否相等
if (nullptr == pRoot)
{
if (k!= blackCount)
{
std::cout << "违反性质四:每条路径中黑色节点的个数必须相同" << std::endl;
return false;
}
return true;
}
// 统计黑色节点的个数
if (pRoot->_color == BLACK)
{
k++;
}
// 检测当前节点与其双亲是否都为红色
PNode pParent = pRoot->_pParent;
if (pParent && pParent->_color == RED && pRoot->_color == RED)
{
std::cout << "违反性质三:没有连在一起的红色节点" << std::endl;
return false;
}
return _IsValidRBTree(pRoot->_pLeft, k, blackCount) &&
_IsValidRBTree(pRoot->_pRight, k, blackCount);
}六、红黑树迭代器的实现
6.1 迭代器的定义
迭代器是红黑树与用户交互的重要接口,它可以方便地遍历红黑树。我们定义迭代器类如下:
cpp
cpp
template<class ValueType, class Pointer, class Reference>
class RBTreeIterator
{
typedef RBTreeNode<ValueType> Node;
typedef RBTreeIterator<ValueType, Pointer, Reference> Self;
public:
RBTreeIterator(Node* node = nullptr) : _pNode(node) {}
Reference operator*() { return _pNode->_data; }
Pointer operator->() { return &(_pNode->_data); }
Self& operator++()
{
_Increament();
return *this;
}
Self operator++(int)
{
Self tmp(*this);
_Increament();
return tmp;
}
Self& operator--()
{
_Decreament();
return *this;
}
Self operator--(int)
{
Self tmp(*this);
_Decreament();
return tmp;
}
bool operator==(const Self& s) const { return _pNode == s._pNode; }
bool operator!=(const Self& s) const { return _pNode!= s._pNode; }
private:
void _Increament()
{
if (_pNode->_pRight)
{
_pNode = _pNode->_pRight;
while (_pNode->_pLeft)
{
_pNode = _pNode->_pLeft;
}
}
else
{
Node* pParent = _pNode->_pParent;
while (pParent && _pNode == pParent->_pRight)
{
_pNode = pParent;
pParent = pParent->_pParent;
}
_pNode = pParent;
}
}
void _Decreament()
{
if (_pNode->_color == RED && _pNode->_pParent->_pParent == _pNode)
{
_pNode = _pNode->_pRight;
}
else if (_pNode->_pLeft)
{
_pNode = _pNode->_pLeft;
while (_pNode->_pRight)
{
_pNode = _pNode->_pRight;
}
}
else
{
Node* pParent = _pNode->_pParent;
while (pParent && _pNode == pParent->_pLeft)
{
_pNode = pParent;
pParent = pParent->_pParent;
}
_pNode = pParent;
}
}
Node* _pNode;
};6.2 迭代器的递增和递减操作
迭代器的递增操作 operator++ 用于找到当前节点的下一个节点。如果当前节点有右子树,那么下一个节点就是右子树中最左侧的节点;如果当前节点没有右子树,则向上查找,直到找到一个是其双亲节点左孩子的节点,该双亲节点就是下一个节点。
迭代器的递减操作 operator-- 则相反,用于找到当前节点的前一个节点。如果当前节点是头结点且颜色为红色,那么前一个节点是右子树中最大的节点;如果当前节点有左子树,那么前一个节点就是左子树中最右侧的节点;如果当前节点没有左子树,则向上查找,直到找到一个是其双亲节点右孩子的节点,该双亲节点就是前一个节点。
七、红黑树模拟实现 map 与 set
7.1 set 的模拟实现
set 是一种关联式容器,其底层结构为红黑树。`在 set 中,每个元素的值同时也是其键值,元素是唯一且有序的。下面是 set 类的模拟实现代码:
cpp
cpp
namespace bit
{
template<class K>
class set
{
private:
// 定义仿函数用于提取键值
struct KeyOfValue
{
const K& operator()(const K& key) const
{
return key;
}
};
// 底层使用红黑树存储数据
typedef RBTree<K, K, KeyOfValue> RBTreeType;
public:
typedef typename RBTreeType::Iterator iterator;
set() {}
// 迭代器相关
iterator begin() { return _tree.Begin(); }
iterator end() { return _tree.End(); }
// 容量相关
size_t size() const { return _tree.Size(); }
bool empty() const { return _tree.Empty(); }
// 插入操作
pair<iterator, bool> insert(const K& data)
{
return _tree.Insert(data);
}
// 清空操作
void clear() { _tree.Clear(); }
// 查找操作
iterator find(const K& key) { return _tree.Find(key); }
private:
RBTreeType _tree;
};
}
在上述代码中,通过定义 KeyOfValue 仿函数,将元素值直接作为键值。然后利用前面实现的红黑树类 RBTree 来存储和管理元素,对外提供 set 容器常用的接口,如插入、查找、遍历等。
7.2 map 的模拟实现
map 也是关联式容器,它存储的是键值对( pair ),其中键值是唯一且有序的,通过键值可以快速查找对应的值。以下是 map 类的模拟实现:
cpp
cpp
namespace bit
{
template<class K, class V>
class map
{
private:
// 定义键值对类型
typedef pair<K, V> valueType;
// 定义仿函数用于提取键值
struct KeyOfValue
{
const K& operator()(const valueType& v) const
{
return v.first;
}
};
// 底层使用红黑树存储数据
typedef RBTree<K, valueType, KeyOfValue> RBTreeType;
public:
typedef typename RBTreeType::Iterator iterator;
map() {}
// 迭代器相关
iterator begin() { return _tree.Begin(); }
iterator end() { return _tree.End(); }
// 容量相关
size_t size() const { return _tree.Size(); }
bool empty() const { return _tree.Empty(); }
// 插入操作
pair<iterator, bool> insert(const valueType& data)
{
return _tree.Insert(data);
}
// 重载 [] 运算符,方便通过键值访问对应的值
V& operator[](const K& key)
{
pair<iterator, bool> ret = _tree.Insert(valueType(key, V()));
return ret.first->second;
}
const V& operator[](const K& key) const
{
iterator it = _tree.Find(key);
return it->second;
}
// 清空操作
void clear() { _tree.Clear(); }
// 查找操作
iterator find(const K& key) { return _tree.Find(key); }
private:
RBTreeType _tree;
};
}在 map 的实现中,通过 KeyOfValue 仿函数从键值对中提取键值。同样基于红黑树实现数据存储和管理,并且重载了 [] 运算符,使得可以像使用数组一样通过键值方便地访问和修改对应的值。
八、总结
红黑树通过巧妙地利用节点颜色和一些性质,在保证树近似平衡的同时,实现了高效的插入、删除和查找操作。在C++ 中, map 和 set 等关联式容器借助红黑树的特性,为我们提供了快速、有序的数据存储和访问方式。通过深入理解红黑树的原理和实现细节,我们不仅能更好地使用这些容器,还能在遇到类似数据组织和查询需求时,灵活运用红黑树来设计高效的数据结构。
希望本文能帮助大家对红黑树及其在C++ 关联式容器中的应用有更清晰、深入的认识。如果有任何疑问或建议,欢迎交流探讨。