1. 基本概念
哈夫曼树(Huffman Tree),又称最优二叉树 ,是一种带权路径长度(WPL, Weighted Path Length)最短的二叉树。它主要用于数据压缩 和编码优化,通过为不同权值的节点分配不同长度的编码,使得高频数据占用更短的编码,从而减少整体存储空间。
2. 关键术语
- 路径(Path):从树的一个节点到另一个节点的分支序列。
- 路径长度(Path Length):路径上的分支数量。
- 带权路径长度(WPL, Weighted Path Length):所有叶子节点的权值乘以其到根节点的路径长度之和
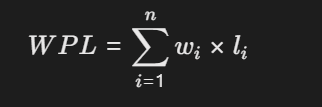
- 其中,wi 是第 i 个叶子节点的权值,li 是其到根节点的路径长度。
- 最优二叉树:具有最小 WPL 的二叉树。
3. 构造哈夫曼树的步骤
假设有 n 个权值 {w1,w2,...,wn},构造哈夫曼树的算法如下:
- 初始化:将每个权值 wi 看作一棵只有根节点的二叉树,构成一个森林 F={T1,T2,...,Tn}。
- 合并最小权值树 :
- 在森林 F 中选取两棵根节点权值最小的树 Ti 和 Tj。
- 合并它们为一棵新树,新树的根节点权值为 wi+wj,左子树为 Ti,右子树为 Tj。
- 将新树加入森林 F,并删除 Ti 和 Tj。
- 重复合并:重复步骤 2,直到森林 F 中只剩下一棵树,即为哈夫曼树。
示例 :
给定权值集合 {5,9,12,13,16,45},构造哈夫曼树的过程如下:
- 初始森林:{5,9,12,13,16,45}
- 合并最小的 5 和 9 → 新树权值 14
森林:{12,13,14,16,45} - 合并最小的 12 和 13 → 新树权值 25
森林:{14,16,25,45} - 合并最小的 14 和 16 → 新树权值 30
森林:{25,30,45} - 合并最小的 25 和 30 → 新树权值 55
森林:{45,55} - 合并 45 和 55 → 最终哈夫曼树
根节点权值 100
最终哈夫曼树结构:
[100]
/ \
[45] [55]
/ \
[25] [30]
/ \ / \
[12][13] [14][16]
/ \
[5] [9]4. 哈夫曼编码
哈夫曼编码是一种前缀编码(Prefix Code),即没有任何一个编码是另一个编码的前缀,从而避免解码时的歧义。
编码规则:
- 左分支 :赋值为
0 - 右分支 :赋值为
1 - 从根节点到叶子节点的路径即为该字符的编码。
示例编码(基于上述哈夫曼树):
给定权值集合 {5,9,12,13,16,45}

| 字符 | 权值 | 编码 |
|---|---|---|
| A | 5 | 0000 |
| B | 9 | 0001 |
| C | 12 | 001 |
| D | 13 | 010 |
| E | 16 | 011 |
| F | 45 | 1 |
计算 WPL (带权路径长度):
WPL=5×4+9×4+12×3+13×3+16×3+45×1=224
5. 哈夫曼树的性质
- 唯一性 :给定权值集合,哈夫曼树的形态可能不唯一(合并顺序不同),但 WPL 相同。
- 最优性:哈夫曼树的 WPL 是最小的。
- 叶子节点数 = 权值个数:哈夫曼树中没有度为 1 的节点(即没有单分支节点)。
6. 应用场景
- 数据压缩(如 ZIP、JPEG、MP3 等格式)。
- 文件存储优化(减少冗余数据)。
- 网络传输(降低带宽占用)。
- 机器学习(决策树、特征选择等)。
7. 总结
- 哈夫曼树是一种带权路径长度最短的二叉树,用于优化数据编码。
- 构造方法:贪心算法,每次合并最小的两个权值。
- 编码方式 :左
0右1,保证前缀无歧义。 - 应用广泛:数据压缩、存储优化等。