决策树-分类
- [1 概念](#1 概念)
- [2 基于信息增益决策树的建立](#2 基于信息增益决策树的建立)
-
- [(1) 信息熵](#(1) 信息熵)
- [(2) 信息增益](#(2) 信息增益)
- [(3) 信息增益决策树建立步骤](#(3) 信息增益决策树建立步骤)
- [3 基于基尼指数决策树的建立(了解)](#3 基于基尼指数决策树的建立(了解))
- [4 sklearn API](#4 sklearn API)
- [5 示例](#5 示例)
1 概念
1、决策节点
通过条件判断 而进行分支选择的节点。如:将某个样本中的属性值(特征值)与决策节点上的值进行比较,从而判断它的流向。
2、叶子节点
没有子节点的节点,表示最终的决策结果。
3、决策树的深度
所有节点的最大层次数。
决策树具有一定的层次结构,根节点的层次数定为0,从下面开始每一层子节点层次数增加
4、决策树优点:
可视化 - 可解释能力-对算力要求低
5、 决策树缺点:
容易产生过拟合,所以不要把深度调整太大了。


| 是动物 | 会飞 | 有羽毛 | |
|---|---|---|---|
| 1麻雀 | 1 | 1 | 1 |
| 2蝙蝠 | 1 | 1 | 0 |
| 3飞机 | 0 | 1 | 0 |
| 4熊猫 | 1 | 0 | 0 |
是否为动物
| 是动物 | 会飞 | 有羽毛 | |
|---|---|---|---|
| 1麻雀 | 1 | 1 | 1 |
| 2蝙蝠 | 1 | 1 | 0 |
| 4熊猫 | 1 | 0 | 0 |
是否会飞
| 是动物 | 会飞 | 有羽毛 | |
|---|---|---|---|
| 1麻雀 | 1 | 1 | 1 |
| 2蝙蝠 | 1 | 1 | 0 |
是否有羽毛
| 是动物 | 会飞 | 有羽毛 | |
|---|---|---|---|
| 1麻雀 | 1 | 1 | 1 |
2 基于信息增益决策树的建立
信息增益决策树倾向于选择取值较多的属性,在有些情况下这类属性可能不会提供太多有价值的信息,算法只能对描述属性为离散型属性的数据集构造决策树。
根据以下信息构建一棵预测是否贷款的决策树。我们可以看到有4个影响因素:职业,年龄,收入和学历。
| 职业 | 年龄 | 收入 | 学历 | 是否贷款 | |
|---|---|---|---|---|---|
| 1 | 工人 | 36 | 5500 | 高中 | 否 |
| 2 | 工人 | 42 | 2800 | 初中 | 是 |
| 3 | 白领 | 45 | 3300 | 小学 | 是 |
| 4 | 白领 | 25 | 10000 | 本科 | 是 |
| 5 | 白领 | 32 | 8000 | 硕士 | 否 |
| 6 | 白领 | 28 | 13000 | 博士 | 是 |
(1) 信息熵
信息熵描述的是不确定性。信息熵越大,不确定性越大。信息熵的值越小,则D的纯度越高。
假设样本集合D共有N类,第k类样本所占比例为,则D的信息熵为

(2) 信息增益
信息增益是一个统计量,用来描述一个属性区分数据样本的能力 。信息增益越大,那么决策树就会越简洁。 这里信息增益的程度用信息熵的变化程度来衡量, 信息增益公式:
(3) 信息增益决策树建立步骤
第一步,计算根节点的信息熵
上表根据是否贷款把样本分成2类样本,"是"占4/6=2/3, "否"占2/6=1/3,
所以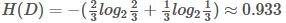
第二步,计算属性的信息增益
<1> "职业"属性的信息增益 在职业中,工人占1/3, 工人中,是否代款各占1/2, 所以有
在职业中,工人占1/3, 工人中,是否代款各占1/2, 所以有

在职业中,白领占2/3, 白领中,是贷款占3/4, 不贷款占1/4, 所以有

所以有 
最后得到职业属性的信息增益为:
<2>" 年龄"属性的信息增益(以35岁为界)

<3> "收入"属性的信息增益(以10000为界,大于等于10000为一类)

<4> "学历"属性的信息增益(以高中为界, 大于等于高中的为一类)

注意:
- 以上年龄使用35为界,收入使用10000为界,学历使用高中为界,实计API使用中,会有一个参数"深度", 属性中具体以多少为界会被根据深度调整。
第三步, 划分属性
对比属性信息增益发现,"收入"和"学历"相等,并且是最高的,所以我们就可以选择"学历"或"收入"作为第一个
决策树的节点, 接下来我们继续重复1,2的做法继续寻找合适的属性节点

3 基于基尼指数决策树的建立(了解)
基尼指数 (Gini Index)是决策树算法中用于评估数据集纯度的一种度量,基尼指数衡量的是数据集的不纯度,或者说分类的不确定性。 在构建决策树时,基尼指数被用来决定如何对数据集进行最优划分,以减少不纯度。
基尼指数的计算
对于一个二分类问题,如果一个节点包含的样本属于正类的概率是 p,则属于负类的概率是 (1-p)。那么,这个节点的基尼指数(Gini(p)) 定义为:

对于多分类问题,如果一个节点包含的样本属于第 k 类的概率是 p k p_k pk,则节点的基尼指数定义为:

基尼指数的意义
- 当一个节点的所有样本都属于同一类别时,基尼指数为 0,表示纯度最高。
- 当一个节点的样本均匀分布在所有类别时,基尼指数最大,表示纯度最低。
决策树中的应用
在构建决策树时,我们希望每个内部节点的子节点能更纯,即基尼指数更小。 因此,选择分割特征和分割点的目标是使子节点的平均基尼指数最小化。具体来说,对于一个特征,我们计算其所有可能的分割点对应的子节点的加权平均基尼指数,然后选择最小化这个值的分割点。这个过程会在所有特征中重复,直到找到最佳的分割特征和分割点。
例如,考虑一个数据集 (D),其中包含 (N) 个样本,特征 (A) 将数据集分割为 ∣ D 1 ∣ |D_1| ∣D1∣和 ∣ D 2 ∣ |D_2| ∣D2∣ ,则特征 (A) 的基尼指数为:

其中 ∣ D 1 ∣ |D_1| ∣D1∣和 ∣ D 2 ∣ |D_2| ∣D2∣ 分别是子集 D 1 D_1 D1 和 D 2 D_2 D2 中的样本数量。
通过这样的方式 ,决策树算法逐步构建一棵树,每一层的节点都尽可能地减少基尼指数,最终达到对数据集的有效分类。
案例:

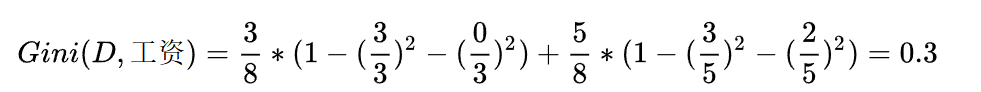
首先工资有两个取值,分别是0和1。当工资=1时,有3个样本。
所以: 同时,在这三个样本中,工作都是好。
同时,在这三个样本中,工作都是好。
所以:

就有了加号左边的式子:
同理,当工资=0时,有5个样本,在这五个样本中,工作有3个是不好,2个是好。
就有了加号右边的式子
同理,可得压力的基尼指数如下:
平台的基尼指数如下:

在计算时,工资和平台的计算方式有明显的不同。因为工资只有两个取值0和1,而平台有三个取值0,1,2。所以在计算时,需要将平台的每一个取值都单独进行计算。比如:当平台=0时,将数据集分为两部分,第一部分是平台=0,第二部分是平台!=0(分母是5的原因)。
根据基尼指数最小准则, 我们优先选择工资或者平台=0作为D的第一特征。
我们选择工资作为第一特征,那么当工资=1时,工作=好,无需继续划分。当工资=0时,需要继续划分。
当工资=0时,继续计算基尼指数:

当平台=0时,基尼指数=0,可以优先选择。
同时,当平台=0时,工作都是好,无需继续划分,当平台=1,2时,工作都是不好,也无需继续划分。直接把1,2放到树的一个结点就可以。
4 sklearn API
py
class sklearn.tree.DecisionTreeClassifier(....)
参数:
criterion "gini" "entropy" 默认为="gini"
当criterion取值为"gini"时采用 基尼不纯度(Gini impurity)算法构造决策树,
当criterion取值为"entropy"时采用信息增益( information gain)算法构造决策树.
max_depth int, 默认为=None 树的最大深度
# 可视化决策树
function sklearn.tree.export_graphviz(estimator, out_file="iris_tree.dot", feature_names=iris.feature_names)
参数:
estimator决策树预估器
out_file生成的文档
feature_names节点特征属性名
功能:
把生成的文档打开,复制出内容粘贴到"http://webgraphviz.com/"中,点击"generate Graph"会生成一个树型的决策树图5 示例
示例1:鸢尾花分类
用决策树对鸢尾花进行分类
python
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
#导入决策树的库
from sklearn.tree import DecisionTreeClassifier,export_graphviz
# 获取数据集
iris=load_iris()
x,y=load_iris(return_X_y=True)
# 数据集划分
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.2,random_state=22,shuffle=True)
# 标准化
transfer=StandardScaler()
x_train=transfer.fit_transform(x_train)
x_test=transfer.transform(x_test)
# 建立决策树的模型(预估器)
model=DecisionTreeClassifier(criterion="entropy")#(criterion="entropy":表示以信息增益的方式进行决策分类
# 训练模型
model.fit(x_train,y_train)
# 模型评估
score=model.score(x_test,y_test)
print("准确率:",score)
index=model.predict([[2,2,3,1]])
print("预测:\n",index,iris.target_names,iris.target_names[index])
"""
准确率: 0.8666666666666667
预测:
[2] ['setosa' 'versicolor' 'virginica'] ['virginica']
"""
# 可视化决策树
export_graphviz(model, out_file="iris_tree.dot", feature_names=iris.feature_names)