【三维重建】【3DGS系列】【深度学习】3DGS的理论基础知识之如何形成高斯椭球
文章目录
前言
在详细解析3DGS代码之前,首要任务是成功运行3DGS代码【理论基础及代码运行(win11下)解析参考教程】,后续学习才有意义。本博客讲解3DGS中如何形成高斯椭球,不涉及具体的模块代码。
参考:3D高斯的理论理解
参考:3d gaussian splatting全解 捏雪球
高斯函数
一维高斯
标准一维高斯函数:
f ( x ) = 1 2 π σ e − x 2 2 f\left( x \right) = \frac{1}{{\sqrt {2\pi\sigma} }}{e^{ - \frac{{{x^2}}}{2}}} f(x)=2πσ 1e−2x2
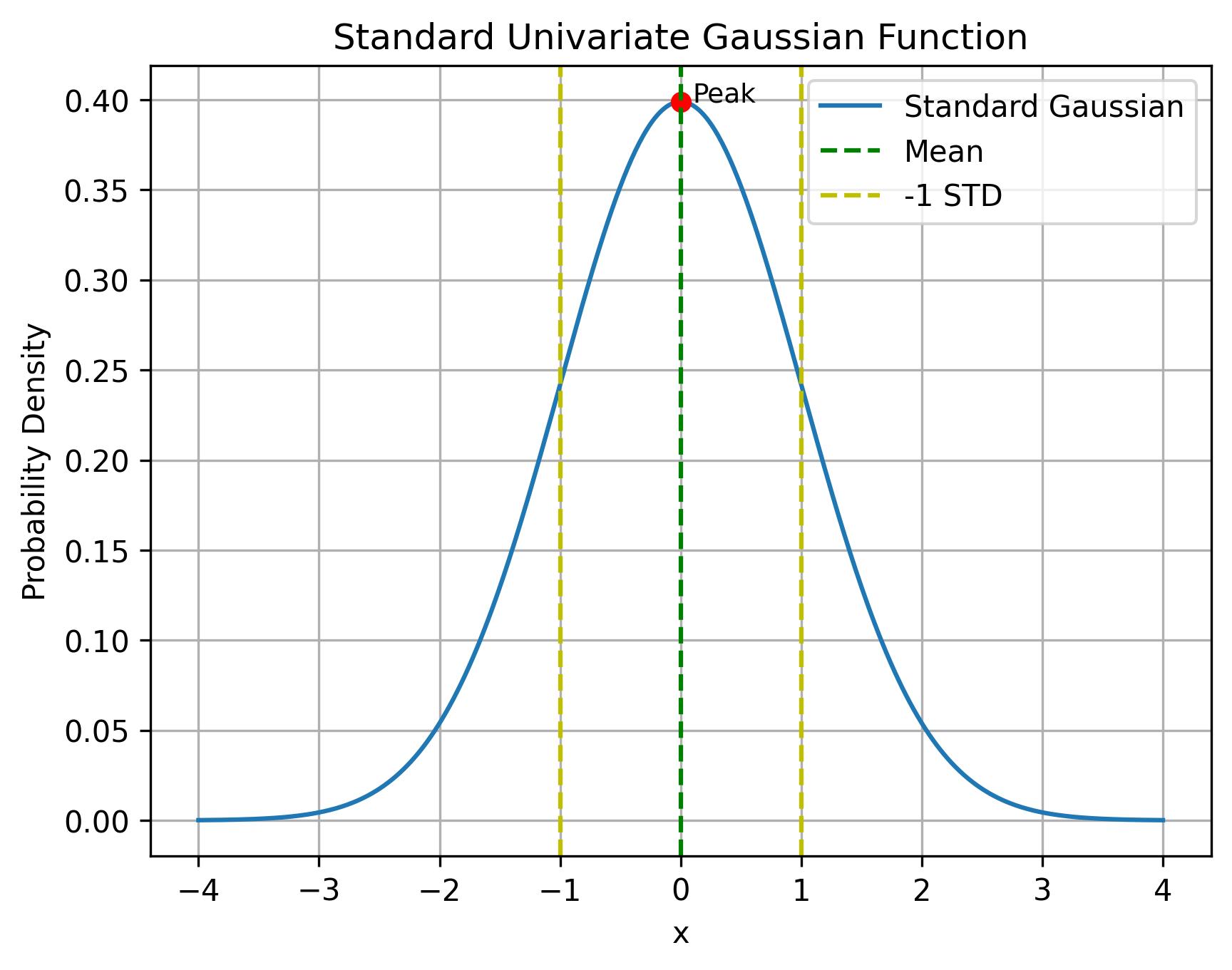
其中的 σ \sigma σ表示高斯函数的方差, μ \mu μ表示高斯函数的均值;标准高斯函数的方差 σ \sigma σ为1,均值 μ \mu μ为0,概率密度之和为1。
python
import numpy as np
import matplotlib.pyplot as plt
# 定义高斯函数
def gaussian(x, mean=0, std=1):
return (1 / (std * np.sqrt(2 * np.pi))) * np.exp(-((x - mean) ** 2) / (2 * std ** 2))
# 生成x轴数据
x = np.linspace(-4, 4, 500)
# 均值和标准差
mean = 0 # 均值 μ
std = 1 # 标准差 σ
# 计算对应y值
y = gaussian(x, mean, std)
# 绘制图形
plt.plot(x, y, label='Standard Gaussian')
# 在均值处标注峰值点
peak_y = gaussian(mean)
plt.plot(0, peak_y, 'ro') # 红色圆圈标记
plt.text(0+0.1, peak_y, 'Peak', fontsize=9)
# 标注均值、±1σ, ±2σ, ±3σ的位置
plt.axvline(x=mean, color='g', linestyle='--', label='Mean')
plt.axvline(x=mean - std, color='y', linestyle='--', label='-1 STD')
plt.axvline(x=mean + std, color='y', linestyle='--')
# 添加图例
plt.legend()
# 图像标题与坐标轴标签
plt.title('Standard Univariate Gaussian Function')
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.grid(True)
# 保存图像(文件名中包含均值和标准差)
filename = f'standard_gaussian_distribution.jpg'
plt.savefig(filename, dpi=300, bbox_inches='tight')
# 显示图像
plt.show()不限制均值和方差,一维高斯函数:
f ( x ) = 1 2 π σ e − ( x − μ ) 2 2 σ 2 f\left( x \right) = \frac{1}{{\sqrt {2\pi\sigma} }}{e^{ - \frac{{{{\left( {x - \mu } \right)}^2}}}{{2{\sigma ^2}}}}} f(x)=2πσ 1e−2σ2(x−μ)2
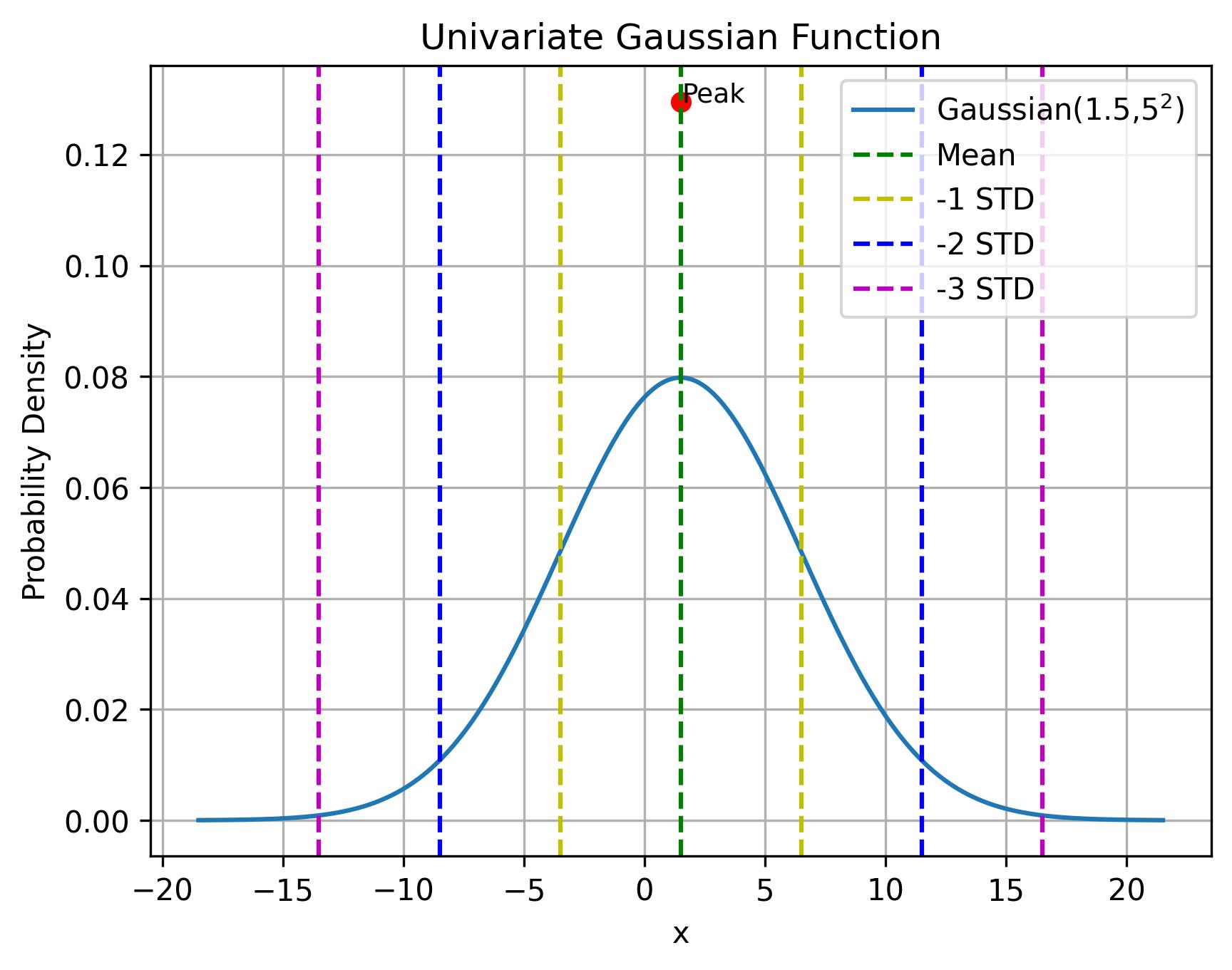
在数学上的意义为将标准高斯函数向右平移 μ \mu μ个单位,函数宽度延展了 σ \sigma σ倍,分别决定了分布的位置和宽度,同时为了保证概率密度函数积分为1, f ( x ) f\left( x \right) f(x) 的高度会下降,因为系数 1 2 π σ \frac{1}{{\sqrt {2\pi\sigma} }} 2πσ 1。
python
import numpy as np
import matplotlib.pyplot as plt
# 定义高斯函数
def gaussian(x, mean=0, std=1):
return (1 / (std * np.sqrt(2 * np.pi))) * np.exp(-((x - mean) ** 2) / (2 * std ** 2))
# 均值和标准差
mean = 1.5 # 均值 μ
std = 5 # 标准差 σ
# 生成x轴数据(根据均值和标准差适当调整范围)
x = np.linspace(mean - 4*std, mean + 4*std, 500)
# 计算对应y值
y = gaussian(x, mean, std)
# 绘制图形
plt.plot(x, y, label=f'Gaussian({mean},{std}$^2$)')
# 在均值处标注峰值点
peak_y = gaussian(mean)
plt.plot(mean, peak_y, 'ro') # 红色圆圈标记
plt.text(mean + 0.05, peak_y, 'Peak', fontsize=9)
# 标注均值、±1σ, ±2σ, ±3σ的位置
plt.axvline(x=mean, color='g', linestyle='--', label='Mean')
plt.axvline(x=mean - std, color='y', linestyle='--', label='-1 STD')
plt.axvline(x=mean + std, color='y', linestyle='--')
plt.axvline(x=mean - 2*std, color='b', linestyle='--', label='-2 STD')
plt.axvline(x=mean + 2*std, color='b', linestyle='--')
plt.axvline(x=mean - 3*std, color='m', linestyle='--', label='-3 STD')
plt.axvline(x=mean + 3*std, color='m', linestyle='--')
# 添加图例
plt.legend()
# 图像标题与坐标轴标签
plt.title('Univariate Gaussian Function')
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.grid(True)
# 保存图像(文件名中包含均值和标准差)
filename = f'gaussian_mu{mean}_sigma{std}.jpg'
plt.savefig(filename, dpi=300, bbox_inches='tight')
# 显示图像
plt.show()多维高斯
- n n n个服从正态分布且互不相关的独立变量 x = [ x 1 , x 2 , . . . , x n ] T x = {\left[ {{x_1},{x_2},...,{x_n}} \right]^T} x=[x1,x2,...,xn]T,其均值为 μ ( x ) = [ μ 1 , μ 2 , . . . , μ n ] T \mu\left( x \right) = {\left[ {{\mu _1},{\mu _2},...,{\mu _n}} \right]^T} μ(x)=[μ1,μ2,...,μn]T,方差为 σ ( x ) = [ σ 1 , σ 2 , . . . , σ n ] T \sigma\left( x \right) = {\left[ {{\sigma_1},{\sigma_2},...,{\sigma_n}} \right]^T} σ(x)=[σ1,σ2,...,σn]T,根据概率论中的概率密度公式有:
f ( x ) = p ( x 1 , x 2 , . . . , x n ) = p ( x 1 ) p ( x 2 ) . . . p ( x n ) = 1 ( 2 π ) n σ 1 σ 1 . . . σ n e − ( x 1 − μ 1 ) 2 2 σ 1 2 − ( x 2 − μ 2 ) 2 2 σ 2 2 . . . − ( x n − μ n ) 2 2 σ n 2 f\left( x \right) = p\left( {{x_1},{x_2},...,{x_n}} \right) = p\left( {{x_1}} \right)p\left( {{x_2}} \right)...p\left( {{x_n}} \right) = \frac{1}{{{{\left( {\sqrt {2\pi } } \right)}^n}{\sigma _1}{\sigma _1}...{\sigma _n}}}{e^{ - \frac{{{{\left( {{x_1} - {\mu _1}} \right)}^2}}}{{2{\sigma _1}^2}} - \frac{{{{\left( {{x_2} - {\mu _2}} \right)}^2}}}{{2{\sigma _2}^2}}... - \frac{{{{\left( {{x_n} - {\mu _n}} \right)}^2}}}{{2{\sigma _n}^2}}}} f(x)=p(x1,x2,...,xn)=p(x1)p(x2)...p(xn)=(2π )nσ1σ1...σn1e−2σ12(x1−μ1)2−2σ22(x2−μ2)2...−2σn2(xn−μn)2
- 将 ( x 1 − μ 1 ) 2 2 σ 1 2 + ( x 2 − μ 2 ) 2 2 σ 2 2 . . . + ( x n − μ n ) 2 2 σ n 2 \frac{{{{\left( {{x_1} - {\mu _1}} \right)}^2}}}{{2{\sigma _1}^2}} + \frac{{{{\left( {{x_2} - {\mu _2}} \right)}^2}}}{{2{\sigma _2}^2}}... + \frac{{{{\left( {{x_n} - {\mu _n}} \right)}^2}}}{{2{\sigma _n}^2}} 2σ12(x1−μ1)2+2σ22(x2−μ2)2...+2σn2(xn−μn)2分解表示:
x 1 − μ 1 , x 2 − μ 2 . . . x n − μ n \] \[ 1 σ 1 2 0 . . . . 0 0 1 σ 2 2 . . . . 0 . . . . . . . . . . . . . . . . 0 0 . . . . 1 σ n 2 \] \[ x 1 − μ 1 , x 2 − μ 2 . . . x n − μ n \] T \\left\[ {{x_1} - {\\mu _1},{x_2} - {\\mu _2}...{x_n} - {\\mu _n}} \\right\]\\left\[ {\\begin{array}{c} {\\frac{1}{{\\sigma _1\^2}}}\&0\&{....}\&0\\\\ 0\&{\\frac{1}{{\\sigma _2\^2}}}\&{....}\&0\\\\ {....}\&{....}\&{....}\&{....}\\\\ 0\&0\&{....}\&{\\frac{1}{{\\sigma _n\^2}}} \\end{array}} \\right\]{\\left\[ {{x_1} - {\\mu _1},{x_2} - {\\mu _2}...{x_n} - {\\mu _n}} \\right\]\^T} \[x1−μ1,x2−μ2...xn−μn\] σ1210....00σ221....0................00....σn21 \[x1−μ1,x2−μ2...xn−μn\]T 用 x − μ x x - {\\mu _x} x−μx表示 \[ x 1 − μ 1 , x 2 − μ 2 . . . x n − μ n \] T {\\left\[ {{x_1} - {\\mu _1},{x_2} - {\\mu _2}...{x_n} - {\\mu _n}} \\right\]\^T} \[x1−μ1,x2−μ2...xn−μn\]T;用协方差矩阵 Σ \\Sigma Σ表示 \[ σ 1 2 0 . . . . 0 0 σ 2 2 . . . . 0 . . . . . . . . . . . . . . . . 0 0 . . . . σ n 2 \] \\left\[ {\\begin{array}{c} {\\sigma _1\^2}\&0\&{....}\&0\\\\ 0\&{\\sigma _2\^2}\&{....}\&0\\\\ {....}\&{....}\&{....}\&{....}\\\\ 0\&0\&{....}\&{\\sigma _n\^2} \\end{array}} \\right\] σ120....00σ22....0................00....σn2 ,则进一步简化为 ( x − μ x ) T ( Σ ) − 1 ( x − μ x ) {\\left( {x - {\\mu _x}} \\right)\^T}{(\\Sigma {} )\^{ - 1}}\\left( {x - {\\mu _x}} \\right) (x−μx)T(Σ)−1(x−μx)。
因此多维正态高斯分布函数:
f ( x ) = 1 ( 2 π ) n ∣ Σ ∣ 1 2 e − ( x − μ x ) T ( Σ ) − 1 ( x − μ x ) 2 f\left( x \right) = \frac{1}{{{{\left( {\sqrt {2\pi } } \right)}^n}{{\left| {\Sigma {} } \right|}^{\frac{1}{2}}}}}{e^{ - \frac{{{{\left( {x - {\mu _x}} \right)}^T}{{(\Sigma {} )}^{ - 1}}\left( {x - {\mu _x}} \right)}}{2}}} f(x)=(2π )n∣Σ∣211e−2(x−μx)T(Σ)−1(x−μx)
- n n n个服从正态分布且的随机变量 x = [ x 1 , x 2 , . . . , x n ] T x = {\left[ {{x_1},{x_2},...,{x_n}} \right]^T} x=[x1,x2,...,xn]T,其均值为 μ ( x ) = [ μ 1 , μ 2 , . . . , μ n ] T \mu\left( x \right) = {\left[ {{\mu _1},{\mu _2},...,{\mu _n}} \right]^T} μ(x)=[μ1,μ2,...,μn]T,方差为 σ ( x ) = [ σ 1 , σ 2 , . . . , σ n ] T \sigma\left( x \right) = {\left[ {{\sigma_1},{\sigma_2},...,{\sigma_n}} \right]^T} σ(x)=[σ1,σ2,...,σn]T,还需要一个协方差矩阵 Σ \Sigma Σ来描述变量之间的相关性。多维正态高斯分布函数依旧是:
f ( x ) = 1 ( 2 π ) n ∣ Σ ∣ 1 2 e − ( x − μ x ) T ( Σ ) − 1 ( x − μ x ) 2 f\left( x \right) = \frac{1}{{{{\left( {\sqrt {2\pi } } \right)}^n}{{\left| {\Sigma {} } \right|}^{\frac{1}{2}}}}}{e^{ - \frac{{{{\left( {x - {\mu _x}} \right)}^T}{{(\Sigma {} )}^{ - 1}}\left( {x - {\mu _x}} \right)}}{2}}} f(x)=(2π )n∣Σ∣211e−2(x−μx)T(Σ)−1(x−μx)
协方差矩阵同样是一个 n × n {\rm{n}} \times {\rm{n}} n×n的矩阵,其元素 Σ i j {\Sigma_{ij}} Σij表示第 i i i个随机变量与第 j j j个随机变量之间的协方差:
Σ = [ σ 1 2 σ 12 . . . . σ 1 n σ 21 σ 2 2 . . . . σ 2 n . . . . . . . . . . . . . . . . σ n 1 σ n 2 . . . . σ n 2 ] \Sigma = \left[ {\begin{array}{c} {\sigma _1^2}&{{\sigma _{12}}}&{....}&{{\sigma _{1n}}}\\ {{\sigma _{21}}}&{\sigma _2^2}&{....}&{{\sigma _{2n}}}\\ {....}&{....}&{....}&{....}\\ {{\sigma _{n1}}}&{{\sigma _{n2}}}&{....}&{\sigma _n^2} \end{array}} \right] Σ= σ12σ21....σn1σ12σ22....σn2................σ1nσ2n....σn2
如果 Σ i j = σ i j = 0 {\Sigma_{ij}}={\sigma _{ij}}=0 Σij=σij=0 说明第 i i i个变量和第 j j j个变量之间没有线性相关性, n n n个服从正态分布且互不相关的独立变量即是这种情况,互相都没有线性相关性;
如果 Σ i j = σ i j ≠ 0 {\Sigma _{ij}}={\sigma _{ij}} \ne 0 Σij=σij=0则说明第 i i i个变量和第 j j j个变量之间存在线性相关性。
椭球
基本定义
在坐标系中椭球方程表示为:
( x − x 0 ) 2 a 2 + ( y − y 0 ) 2 b 2 + ( z − z 0 ) 2 c 2 = 1 \frac{{{{\left( {x - {x_0}} \right)}^2}}}{{{a^2}}} + \frac{{{{\left( {y - {y_0}} \right)}^2}}}{{{b^2}}} + \frac{{{{\left( {z - {z_0}} \right)}^2}}}{{{c^2}}} = 1 a2(x−x0)2+b2(y−y0)2+c2(z−z0)2=1
椭球的中心位于空间中的某一点 ( x 0 , y 0 , z 0 ) \left( {{x_0},{y_0},{z_0}} \right) (x0,y0,z0),其中, a a a、 b b b和 c c c分别是椭球沿 x x x、 y y y和 z z z轴方向的半轴长度。如果 a = b = c a=b=c a=b=c,则该图形是一个球体。
当椭球中心点位于坐标原点 ( 0 , 0 , 0 ) (0, 0, 0) (0,0,0)时,标准椭球(中心位于原点且轴与坐标轴对齐的椭球)的方程可以表示为:
x 2 a 2 + y 2 b 2 + z 2 c 2 = 1 \frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} + \frac{{{z^2}}}{{{c^2}}} = 1 a2x2+b2y2+c2z2=1
一般二次形式
用二次方程来表示三维空间中任意位置、任意方向的椭球。这种形式可以涵盖椭球的中心不在原点、主轴不与坐标轴对齐的情况。
主轴与坐标轴对齐的情况: 通过展开椭球方程,将其转化为一个一般的二次曲面形式(即包含 x 2 x^2 x2 、 y 2 y^2 y2、 z 2 z^2 z2、一次项和常数项的形式):
- 展开平方项:
( x − x 0 ) 2 a 2 = x 2 − 2 x x 0 + x 0 2 a 2 \frac{{{{\left( {x - {x_0}} \right)}^2}}}{{{a^2}}} = \frac{{{x^2} - 2x{x_0} + {x_0}^2}}{{{a^2}}} a2(x−x0)2=a2x2−2xx0+x02
( y − y 0 ) 2 b 2 = y 2 − 2 y y 0 + y 0 2 b 2 \frac{{{{\left( {y - {y_0}} \right)}^2}}}{{{b^2}}} = \frac{{{y^2} - 2y{y_0} + {y_0}^2}}{{{b^2}}} b2(y−y0)2=b2y2−2yy0+y02
( z − z 0 ) 2 c 2 = z 2 − 2 z z 0 + z 0 2 c 2 \frac{{{{\left( {z - {z_0}} \right)}^2}}}{{{c^2}}} = \frac{{{z^2} - 2z{z_0} + {z_0}^2}}{{{c^2}}} c2(z−z0)2=c2z2−2zz0+z02 - 整理为一般二次形式:
x 2 a 2 + y 2 b 2 + z 2 b 2 − 2 x x 0 a 2 − 2 y y 0 b 2 − 2 z z 0 c 2 + ( x 0 2 a 2 + y 0 2 b 2 + z 0 2 c 2 ) = 1 \frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} + \frac{{{z^2}}}{{{b^2}}} - \frac{{2x{x_0}}}{{{a^2}}} - \frac{{2y{y_0}}}{{{b^2}}} - \frac{{2z{z_0}}}{{{c^2}}} + (\frac{{{x_0}^2}}{{{a^2}}} + \frac{{{y_0}^2}}{{{b^2}}} + \frac{{{z_0}^2}}{{{c^2}}}) = 1 a2x2+b2y2+b2z2−a22xx0−b22yy0−c22zz0+(a2x02+b2y02+c2z02)=1
一般二次形式的格式如下:
A x 2 + B y 2 + C z 2 + D x + E y + F z + G = 1 A{x^2} + B{y^2} + C{z^2} + Dx + Ey + Fz + G = 1 Ax2+By2+Cz2+Dx+Ey+Fz+G=1
椭球的中心位于空间中的某一点 ( x 0 , y 0 , z 0 ) \left( {{x_0},{y_0},{z_0}} \right) (x0,y0,z0),对应地: A = 1 a 2 A = \frac{1}{{{a^2}}} A=a21; B = 1 b 2 B = \frac{1}{{{b^2}}} B=b21; C = 1 c 2 C = \frac{1}{{{c^2}}} C=c21; D = 2 x 0 a 2 D = \frac{{2{x_0}}}{{{a^2}}} D=a22x0; E = 2 x 0 b 2 E = \frac{{2{x_0}}}{{{b^2}}} E=b22x0; F = 2 x 0 z 2 F = \frac{{2{x_0}}}{{{z^2}}} F=z22x0; G = ( x 0 2 a 2 + y 0 2 b 2 + z 0 2 c 2 ) G = (\frac{{{x_0}^2}}{{{a^2}}} + \frac{{{y_0}^2}}{{{b^2}}} + \frac{{{z_0}^2}}{{{c^2}}}) G=(a2x02+b2y02+c2z02)。
当椭球中心点位于坐标原点 ( 0 , 0 , 0 ) (0, 0, 0) (0,0,0)时:
A x 2 + B y 2 + C z 2 = 1 A{x^2} + B{y^2} + C{z^2} = 1 Ax2+By2+Cz2=1
主轴不与坐标轴对齐的情况(常见情形): 椭球中心点 ( x 0 , y 0 , z 0 ) {\rm{(}}{{\rm{x}}_0}{\rm{,}}{{\rm{y}}_0}{\rm{,}}{{\rm{z}}_0}{\rm{)}} (x0,y0,z0)平移到原点,然后椭球经过绕 z z z轴旋转 α \alpha α,绕 y y y轴旋转 β \beta β,绕 x x x轴旋转 γ \gamma γ。
- 中心点 ( x 0 , y 0 , z 0 ) {\rm{(}}{{\rm{x}}_0}{\rm{,}}{{\rm{y}}_0}{\rm{,}}{{\rm{z}}_0}{\rm{)}} (x0,y0,z0)平移到坐标原点:
x ′ = x − x 0 y ′ = y − y 0 z ′ = z − z 0 \begin{array}{l} {x\prime} = x - {x_0}\\ {y\prime} = y - {y_0}\\ {z\prime} = z - {z_0} \end{array} x′=x−x0y′=y−y0z′=z−z0 - 绕 z z z轴旋转 α \alpha α,旋转矩阵 R z ( α ) {R_{\rm{z}}}\left( \alpha \right) Rz(α):
R z ( α ) = [ cos α − sin α 0 sin α cos α 0 0 0 1 ] {R_{\rm{z}}}\left( \alpha \right) = \left[ {\begin{array}{c} {\cos \alpha }&{ - \sin \alpha }&0\\ {\sin \alpha }&{\cos \alpha }&0\\ 0&0&1 \end{array}} \right] Rz(α)= cosαsinα0−sinαcosα0001
旋转后的坐标 ( x ′ ′ , y ′ ′ , z ′ ′ ) {\rm{(}}{{\rm{x}}\prime\prime}{\rm{,}}{{\rm{y}}\prime\prime}{\rm{,}}{{\rm{z}}\prime\prime}{\rm{)}} (x′′,y′′,z′′)由坐标 ( x ′ , y ′ , z ′ ) {\rm{(}}{{\rm{x}}\prime}{\rm{,}}{{\rm{y}}\prime}{\rm{,}}{{\rm{z}}\prime}{\rm{)}} (x′,y′,z′)计算得出:x ′ ′ y ′ ′ z ′ ′ \] = R x ( α ) \[ x ′ x ′ x ′ \] \\left\[ {\\begin{array}{c} {{x\\prime\\prime}}\\\\ {{y\\prime\\prime}}\\\\ {{z\\prime\\prime}} \\end{array}} \\right\] = {R_x}\\left( \\alpha \\right)\\left\[ {\\begin{array}{c} {{x\\prime}}\\\\ {{x\\prime}}\\\\ {{x\\prime}} \\end{array}} \\right\] x′′y′′z′′ =Rx(α) x′x′x′ 其中 ( x ′ ′ , y ′ ′ , z ′ ′ ) {\\rm{(}}{{\\rm{x}}\\prime\\prime}{\\rm{,}}{{\\rm{y}}\\prime\\prime}{\\rm{,}}{{\\rm{z}}\\prime\\prime}{\\rm{)}} (x′′,y′′,z′′)的值分别为: x ′ ′ = x ′ cos α − y ′ sin α y ′ ′ = x ′ sin α + y ′ cos α z ′ ′ = z ′ \\begin{array}{l} {{x\\prime\\prime} = {x\\prime}\\cos \\alpha - {y\\prime}\\sin \\alpha }\\\\ {{y\\prime\\prime} = {x\\prime}\\sin \\alpha + {y\\prime}\\cos \\alpha }\\\\ {{z\\prime\\prime} = {z\\prime}} \\end{array} x′′=x′cosα−y′sinαy′′=x′sinα+y′cosαz′′=z′
R y ( β ) = [ cos β 0 sin β 0 1 0 − sin β 0 cos β ] {R_y}\left( \beta \right) = \left[ {\begin{array}{c} {\cos \beta }&0&{\sin \beta }\\ 0&1&0\\ { - \sin \beta }&0&{\cos \beta } \end{array}} \right] Ry(β)= cosβ0−sinβ010sinβ0cosβ
旋转后的坐标 ( x ′ ′ ′ , y ′ ′ ′ , z ′ ′ ′ ) {\rm{(}}{{\rm{x}}\prime\prime\prime}{\rm{,}}{{\rm{y}}\prime\prime\prime}{\rm{,}}{{\rm{z}}\prime\prime\prime}{\rm{)}} (x′′′,y′′′,z′′′)由原始坐标 ( x ′ ′ , y ′ ′ , z ′ ′ ) {\rm{(}}{{\rm{x}}\prime\prime}{\rm{,}}{{\rm{y}}\prime\prime}{\rm{,}}{{\rm{z}}\prime\prime}{\rm{)}} (x′′,y′′,z′′)计算得出:x ′ ′ ′ y ′ ′ ′ z ′ ′ ′ \] = R y ( β ) \[ x ′ ′ y ′ ′ z ′ ′ \] \\left\[ {\\begin{array}{c} {{x\\prime\\prime\\prime}}\\\\ {{y\\prime\\prime\\prime}}\\\\ {{z\\prime\\prime\\prime}} \\end{array}} \\right\] = {R_y}\\left( \\beta \\right)\\left\[ {\\begin{array}{c} {{x\\prime\\prime}}\\\\ {{y\\prime\\prime}}\\\\ {{z\\prime\\prime}} \\end{array}} \\right\] x′′′y′′′z′′′ =Ry(β) x′′y′′z′′ 其中 ( x ′ ′ ′ , y ′ ′ ′ , z ′ ′ ′ ) {\\rm{(}}{{\\rm{x}}\\prime\\prime\\prime}{\\rm{,}}{{\\rm{y}}\\prime\\prime\\prime}{\\rm{,}}{{\\rm{z}}\\prime\\prime\\prime}{\\rm{)}} (x′′′,y′′′,z′′′)的值分别为: x ′ ′ ′ = x ′ ′ cos β + z ′ ′ sin β = ( x ′ cos α − y ′ sin α ) cos β + z ′ sin β y ′ ′ ′ = y ′ ′ = x ′ sin α + y ′ cos α z ′ ′ ′ = − x ′ ′ sin β + z 1 cos β = − ( x ′ cos α − y ′ sin α ) sin β + z ′ cos β \\begin{array}{l} {{x\\prime\\prime\\prime} = {x\\prime\\prime}\\cos \\beta + {z\\prime\\prime}\\sin \\beta = (x\\prime\\cos \\alpha - y\\prime\\sin \\alpha )\\cos \\beta + z\\prime\\sin \\beta }\\\\ {{y\\prime\\prime\\prime} = {y\\prime\\prime} = x\\prime\\sin \\alpha + y\\prime\\cos \\alpha }\\\\ {{z\\prime\\prime\\prime} = - {x\\prime\\prime}\\sin \\beta + {z_1}\\cos \\beta = - (x\\prime\\cos \\alpha - y\\prime\\sin \\alpha )\\sin \\beta + z\\prime\\cos \\beta } \\end{array} x′′′=x′′cosβ+z′′sinβ=(x′cosα−y′sinα)cosβ+z′sinβy′′′=y′′=x′sinα+y′cosαz′′′=−x′′sinβ+z1cosβ=−(x′cosα−y′sinα)sinβ+z′cosβ
R z ( γ ) = [ 1 0 0 0 cos γ − sin γ 0 sin γ cos γ ] {R_z}\left( \gamma \right) = \left[ {\begin{array}{c} 1&0&0\\ 0&{\cos \gamma }&{ - \sin \gamma }\\ 0&{\sin \gamma }&{\cos \gamma } \end{array}} \right] Rz(γ)= 1000cosγsinγ0−sinγcosγ
旋转后的坐标 ( x ′ ′ ′ ′ , y ′ ′ ′ ′ , z ′ ′ ′ ′ ) {\rm{(}}{{\rm{x}}\prime\prime\prime\prime}{\rm{,}}{{\rm{y}}\prime\prime\prime\prime}{\rm{,}}{{\rm{z}}\prime\prime\prime\prime}{\rm{)}} (x′′′′,y′′′′,z′′′′)由原始坐标 ( x ′ ′ ′ , y ′ ′ ′ , z ′ ′ ′ ) {\rm{(}}{{\rm{x}}\prime\prime\prime}{\rm{,}}{{\rm{y}}\prime\prime\prime}{\rm{,}}{{\rm{z}}\prime\prime\prime}{\rm{)}} (x′′′,y′′′,z′′′)计算得出:x ′ ′ ′ ′ y ′ ′ ′ ′ z ′ ′ ′ ′ \] = R z ( γ ) \[ x ′ ′ ′ y ′ ′ ′ z ′ ′ ′ \] \\left\[ {\\begin{array}{c} {{x\\prime\\prime\\prime\\prime}}\\\\ {{y\\prime\\prime\\prime\\prime}}\\\\ {{z\\prime\\prime\\prime\\prime}} \\end{array}} \\right\] = {R_z}\\left( \\gamma \\right)\\left\[ {\\begin{array}{c} {{x\\prime\\prime\\prime}}\\\\ {{y\\prime\\prime\\prime}}\\\\ {{z\\prime\\prime\\prime}} \\end{array}} \\right\] x′′′′y′′′′z′′′′ =Rz(γ) x′′′y′′′z′′′ 其中 ( x ′ ′ ′ ′ , y ′ ′ ′ ′ , z ′ ′ ′ ′ ) {\\rm{(}}{{\\rm{x}}\\prime\\prime\\prime\\prime}{\\rm{,}}{{\\rm{y}}\\prime\\prime\\prime\\prime}{\\rm{,}}{{\\rm{z}}\\prime\\prime\\prime\\prime}{\\rm{)}} (x′′′′,y′′′′,z′′′′)的值分别为: x ′ ′ ′ ′ = x ′ ′ ′ = ( x ′ cos α − y ′ sin α ) cos β + z ′ sin β y ′ ′ ′ ′ = y ′ ′ ′ cos γ − z ′ ′ ′ sin γ = ( x ′ sin α + y ′ cos α ) cos γ − ( − ( x ′ cos α − y ′ sin α ) sin β + z ′ cos β ) sin γ z ′ ′ ′ ′ = y ′ ′ ′ sin γ + z ′ ′ ′ cos γ = ( x ′ sin α + y ′ cos α ) sin γ + ( − ( x ′ cos α − y ′ sin α ) sin β + z ′ cos β ) cos γ \\begin{array}{l} {{x\\prime\\prime\\prime\\prime} = {x\\prime\\prime\\prime} = (x\\prime\\cos \\alpha - y\\prime\\sin \\alpha )\\cos \\beta + z\\prime\\sin \\beta }\\\\ {{y\\prime\\prime\\prime\\prime} = {y\\prime\\prime\\prime}\\cos \\gamma - {z\\prime\\prime\\prime}\\sin \\gamma = (x\\prime\\sin \\alpha + y\\prime\\cos \\alpha )\\cos \\gamma - ( - (x\\prime\\cos \\alpha - y\\prime\\sin \\alpha )\\sin \\beta + z\\prime\\cos \\beta )\\sin \\gamma }\\\\ {{z\\prime\\prime\\prime\\prime} = {y\\prime\\prime\\prime}\\sin \\gamma + {z\\prime\\prime\\prime}\\cos \\gamma = (x\\prime\\sin \\alpha + y\\prime\\cos \\alpha )\\sin \\gamma + ( - (x\\prime\\cos \\alpha - y\\prime\\sin \\alpha )\\sin \\beta + z\\prime\\cos \\beta )\\cos \\gamma } \\end{array} x′′′′=x′′′=(x′cosα−y′sinα)cosβ+z′sinβy′′′′=y′′′cosγ−z′′′sinγ=(x′sinα+y′cosα)cosγ−(−(x′cosα−y′sinα)sinβ+z′cosβ)sinγz′′′′=y′′′sinγ+z′′′cosγ=(x′sinα+y′cosα)sinγ+(−(x′cosα−y′sinα)sinβ+z′cosβ)cosγ 将坐标 ( x ′ , y ′ , z ′ ) {\\rm{(}}{{\\rm{x}}\\prime}{\\rm{,}}{{\\rm{y}}\\prime}{\\rm{,}}{{\\rm{z}}\\prime}{\\rm{)}} (x′,y′,z′)转化成 ( x , y , z ) ({\\rm{x}},{\\rm{y}},{\\rm{z}}) (x,y,z): x ′ ′ ′ ′ = ( ( x − x 0 ) cos α − ( y − y 0 ) sin α ) cos β + ( z − z 0 ) sin β y ′ ′ ′ ′ = ( ( x − x 0 ) sin α + ( y − y 0 ) cos α ) cos γ − ( − ( ( x − x 0 ) cos α − ( y − y 0 ) sin α ) sin β + ( z − z 0 ) cos β ) sin γ z ′ ′ ′ ′ = ( ( x − x 0 ) sin α + ( y − y 0 ) cos α ) sin γ + ( − ( ( x − x 0 ) cos α − ( y − y 0 ) sin α ) sin β + ( z − z 0 ) cos β ) cos γ \\begin{array}{l} {{x\\prime\\prime\\prime\\prime} = ((x - {x_0})\\cos \\alpha - (y - {y_0})\\sin \\alpha )\\cos \\beta + (z - {z_0})\\sin \\beta }\\\\ {{y\\prime\\prime\\prime\\prime} = ((x - {x_0})\\sin \\alpha + (y - {y_0})\\cos \\alpha )\\cos \\gamma - ( - ((x - {x_0})\\cos \\alpha - (y - {y_0})\\sin \\alpha )\\sin \\beta + (z - {z_0})\\cos \\beta )\\sin \\gamma }\\\\ {{z\\prime\\prime\\prime\\prime} = ((x - {x_0})\\sin \\alpha + (y - {y_0})\\cos \\alpha )\\sin \\gamma + ( - ((x - {x_0})\\cos \\alpha - (y - {y_0})\\sin \\alpha )\\sin \\beta + (z - {z_0})\\cos \\beta )\\cos \\gamma } \\end{array} x′′′′=((x−x0)cosα−(y−y0)sinα)cosβ+(z−z0)sinβy′′′′=((x−x0)sinα+(y−y0)cosα)cosγ−(−((x−x0)cosα−(y−y0)sinα)sinβ+(z−z0)cosβ)sinγz′′′′=((x−x0)sinα+(y−y0)cosα)sinγ+(−((x−x0)cosα−(y−y0)sinα)sinβ+(z−z0)cosβ)cosγ
x ′ ′ ′ ′ 2 a 2 + y ′ ′ ′ ′ 2 b 2 + z ′ ′ ′ ′ 2 c 2 = 1 \frac{{{x\prime\prime\prime\prime^2}}}{{{a^2}}} + \frac{{{y\prime\prime\prime\prime^2}}}{{{b^2}}} + \frac{{{z\prime\prime\prime\prime^2}}}{{{c^2}}} = 1 a2x′′′′2+b2y′′′′2+c2z′′′′2=1
总的旋转矩阵为:
R = R x ( γ ) R y ( β ) R z ( α ) = [ r 11 r 12 r 13 r 21 r 22 r 23 r 31 r 32 r 33 ] = [ cos α cos β cos α sin β sin γ − sin α cos γ cos α sin β cos γ + sin α sin γ sin α cos β sin α sin β sin γ + cos α cos γ sin α sin β cos γ − cos α sin γ − sin β cos β sin γ − cos β cos γ ] R = {R_x}\left( \gamma \right){R_y}\left( \beta \right){R_z}\left( \alpha \right) = \left[ {\begin{array}{c} {{r_{11}}}&{{r_{12}}}&{{r_{13}}}\\ {{r_{21}}}&{{r_{22}}}&{{r_{23}}}\\ {{r_{31}}}&{{r_{32}}}&{{r_{33}}} \end{array}} \right] = \left[ {\begin{array}{c} {\cos \alpha \cos \beta }&{\cos \alpha \sin \beta \sin \gamma - \sin \alpha \cos \gamma }&{\cos \alpha \sin \beta \cos \gamma + \sin \alpha \sin \gamma }\\ {\sin \alpha \cos \beta }&{\sin \alpha \sin \beta \sin \gamma + \cos \alpha \cos \gamma }&{\sin \alpha \sin \beta \cos \gamma - \cos \alpha \sin \gamma }\\ { - \sin \beta }&{\cos \beta \sin \gamma }&{ - \cos \beta \cos \gamma } \end{array}} \right] R=Rx(γ)Ry(β)Rz(α)= r11r21r31r12r22r32r13r23r33 = cosαcosβsinαcosβ−sinβcosαsinβsinγ−sinαcosγsinαsinβsinγ+cosαcosγcosβsinγcosαsinβcosγ+sinαsinγsinαsinβcosγ−cosαsinγ−cosβcosγ
展开并整理此方程,得到一般二次形式:
A x 2 + B y 2 + C z 2 + D x y + E x z + F y z + + G x + H y + I z + J = 0 A{{\rm{x}}^2} + B{y^2} + C{z^2} + Dxy + Exz + Fyz + + Gx + Hy + Iz + J = 0 Ax2+By2+Cz2+Dxy+Exz+Fyz++Gx+Hy+Iz+J=0
二次项系数:
A = r 11 2 a 2 + r 21 2 b 2 + r 31 2 c 2 B = r 12 2 a 2 + r 22 2 b 2 + r 32 2 c 2 C = r 13 2 a 2 + r 23 2 b 2 + r 33 2 c 2 \begin{array}{l} A = \frac{{r_{11}^2}}{{{a^2}}} + \frac{{r_{21}^2}}{{{b^2}}} + \frac{{r_{31}^2}}{{{c^2}}}\\ B = \frac{{r_{12}^2}}{{{a^2}}} + \frac{{r_{22}^2}}{{{b^2}}} + \frac{{r_{32}^2}}{{{c^2}}}\\ C = \frac{{r_{13}^2}}{{{a^2}}} + \frac{{r_{23}^2}}{{{b^2}}} + \frac{{r_{33}^2}}{{{c^2}}} \end{array} A=a2r112+b2r212+c2r312B=a2r122+b2r222+c2r322C=a2r132+b2r232+c2r332
交叉项系数:
D = 2 ( r 11 r 12 a 2 + r 21 r 22 b 2 + r 31 r 32 c 2 ) E = 2 ( r 11 r 13 a 2 + r 21 r 23 b 2 + r 31 r 33 c 2 ) F = 2 ( r 12 r 13 a 2 + r 22 r 23 b 2 + r 32 r 33 c 2 ) \begin{array}{l} D = 2(\frac{{{r_{11}}{r_{12}}}}{{{a^2}}} + \frac{{{r_{21}}{r_{22}}}}{{{b^2}}} + \frac{{{r_{31}}{r_{32}}}}{{{c^2}}})\\ E = 2(\frac{{{r_{11}}{r_{13}}}}{{{a^2}}} + \frac{{{r_{21}}{r_{23}}}}{{{b^2}}} + \frac{{{r_{31}}{r_{33}}}}{{{c^2}}})\\ F = 2(\frac{{{r_{12}}{r_{13}}}}{{{a^2}}} + \frac{{{r_{22}}{r_{23}}}}{{{b^2}}} + \frac{{{r_{32}}{r_{33}}}}{{{c^2}}}) \end{array} D=2(a2r11r12+b2r21r22+c2r31r32)E=2(a2r11r13+b2r21r23+c2r31r33)F=2(a2r12r13+b2r22r23+c2r32r33)
一次项系数:
G = − 2 ( x 0 a 2 r 11 2 + y 0 b 2 r 21 2 + z 0 c 2 r 31 2 + x 0 b 2 ( 2 r 11 r 21 ) + x 0 c 2 ( 2 r 11 r 31 ) + y 0 a 2 ( 2 r 11 r 21 ) + y 0 c 2 ( 2 r 21 r 31 ) + z 0 a 2 ( 2 r 11 r 31 ) + z 0 b 2 ( 2 r 21 r 31 ) ) H = − 2 ( x 0 a 2 r 12 2 + y 0 b 2 r 22 2 + z 0 c 2 r 32 2 + x 0 b 2 ( 2 r 12 r 22 ) + x 0 c 2 ( 2 r 12 r 32 ) + y 0 a 2 ( 2 r 12 r 22 ) + y 0 c 2 ( 2 r 22 r 32 ) + z 0 a 2 ( 2 r 12 r 32 ) + z 0 b 2 ( 2 r 22 r 32 ) ) G = − 2 ( x 0 a 2 r 13 2 + y 0 b 2 r 23 2 + z 0 c 2 r 33 2 + x 0 b 2 ( 2 r 13 r 23 ) + x 0 c 2 ( 2 r 13 r 33 ) + y 0 a 2 ( 2 r 13 r 23 ) + y 0 c 2 ( 2 r 23 r 33 ) + z 0 a 2 ( 2 r 13 r 33 ) + z 0 b 2 ( 2 r 23 r 33 ) ) \begin{array}{l} G = - 2\left( {\frac{{{x_0}}}{{{a^2}}}r_{11}^2 + \frac{{{y_0}}}{{{b^2}}}r_{21}^2 + \frac{{{z_0}}}{{{c^2}}}r_{31}^2 + \frac{{{x_0}}}{{{b^2}}}(2{r_{11}}{r_{21}}) + \frac{{{x_0}}}{{{c^2}}}(2{r_{11}}{r_{31}}) + \frac{{{y_0}}}{{{a^2}}}(2{r_{11}}{r_{21}}) + \frac{{{y_0}}}{{{c^2}}}(2{r_{21}}{r_{31}}) + \frac{{{z_0}}}{{{a^2}}}(2{r_{11}}{r_{31}}) + \frac{{{z_0}}}{{{b^2}}}(2{r_{21}}{r_{31}})} \right)\\ H = - 2\left( {\frac{{{x_0}}}{{{a^2}}}r_{12}^2 + \frac{{{y_0}}}{{{b^2}}}r_{22}^2 + \frac{{{z_0}}}{{{c^2}}}r_{32}^2 + \frac{{{x_0}}}{{{b^2}}}(2{r_{12}}{r_{22}}) + \frac{{{x_0}}}{{{c^2}}}(2{r_{12}}{r_{32}}) + \frac{{{y_0}}}{{{a^2}}}(2{r_{12}}{r_{22}}) + \frac{{{y_0}}}{{{c^2}}}(2{r_{22}}{r_{32}}) + \frac{{{z_0}}}{{{a^2}}}(2{r_{12}}{r_{32}}) + \frac{{{z_0}}}{{{b^2}}}(2{r_{22}}{r_{32}})} \right)\\ G = - 2\left( {\frac{{{x_0}}}{{{a^2}}}r_{13}^2 + \frac{{{y_0}}}{{{b^2}}}r_{23}^2 + \frac{{{z_0}}}{{{c^2}}}r_{33}^2 + \frac{{{x_0}}}{{{b^2}}}(2{r_{13}}{r_{23}}) + \frac{{{x_0}}}{{{c^2}}}(2{r_{13}}{r_{33}}) + \frac{{{y_0}}}{{{a^2}}}(2{r_{13}}{r_{23}}) + \frac{{{y_0}}}{{{c^2}}}(2{r_{23}}{r_{33}}) + \frac{{{z_0}}}{{{a^2}}}(2{r_{13}}{r_{33}}) + \frac{{{z_0}}}{{{b^2}}}(2{r_{23}}{r_{33}})} \right) \end{array} G=−2(a2x0r112+b2y0r212+c2z0r312+b2x0(2r11r21)+c2x0(2r11r31)+a2y0(2r11r21)+c2y0(2r21r31)+a2z0(2r11r31)+b2z0(2r21r31))H=−2(a2x0r122+b2y0r222+c2z0r322+b2x0(2r12r22)+c2x0(2r12r32)+a2y0(2r12r22)+c2y0(2r22r32)+a2z0(2r12r32)+b2z0(2r22r32))G=−2(a2x0r132+b2y0r232+c2z0r332+b2x0(2r13r23)+c2x0(2r13r33)+a2y0(2r13r23)+c2y0(2r23r33)+a2z0(2r13r33)+b2z0(2r23r33))
常数项:
J = x 0 2 a 2 + y 0 2 b 2 + z 0 2 c 2 − 1 J = \frac{{x_0^2}}{{{a^2}}} + \frac{{y_0^2}}{{{b^2}}} + \frac{{z_0^2}}{{{c^2}}} - 1 J=a2x02+b2y02+c2z02−1
3D高斯椭球
3D高斯与椭球的关系
回顾了多维高斯和椭球的基础知识,本小节终于到了解释3D高斯明明是个分布,为什么可以是个椭球。
三维正态分布的概率密度函数可以表示为:
f ( [ x , y , z ] ) = 1 ( 2 π ) 3 ∣ Σ ∣ 1 2 e − ( x − μ x ) T ( Σ ) − 1 ( x − μ x ) 2 f\left( {[x,y,z]} \right) = \frac{1}{{{{\left( {\sqrt {2\pi } } \right)}^3}{{\left| \Sigma \right|}^{\frac{1}{2}}}}}{e^{ - \frac{{{{\left( {x - {\mu _x}} \right)}^T}{{(\Sigma )}^{ - 1}}\left( {x - {\mu _x}} \right)}}{2}}} f([x,y,z])=(2π )3∣Σ∣211e−2(x−μx)T(Σ)−1(x−μx)
μ \mu μ是均值向量, μ 1 \mu _1 μ1、 μ 2 \mu _2 μ2、 μ 3 \mu _3 μ3分别是 x x x、 y y y、 z z z的均值:
μ = [ μ 1 μ 2 μ 3 ] \mu = \left[ {\begin{array}{c} {{\mu _1}}\\ {{\mu _2}}\\ {{\mu _3}} \end{array}} \right] μ= μ1μ2μ3
Σ \Sigma Σ是协方差矩阵,它是一个 3 × 3 3×3 3×3的矩阵, σ 1 2 \sigma _1^2 σ12、 σ 2 2 \sigma _2^2 σ22、 σ 3 2 \sigma _3^2 σ32分别是 x x x、 y y y、 z z z的方差, σ 12 \sigma _{12} σ12、 σ 13 \sigma _{13} σ13、 σ 23 \sigma _{23} σ23分别是 x x x与 y y y、 x x x与 z z z、 y y y与 z z z的协方差:
Σ = [ σ 1 2 σ 12 σ 13 σ 21 σ 2 2 σ 23 σ 31 σ 32 σ 3 2 ] \Sigma = \left[ {\begin{array}{c} {\sigma _1^2}&{{\sigma _{12}}}&{{\sigma _{13}}}\\ {{\sigma _{21}}}&{\sigma _2^2}&{{\sigma _{23}}}\\ {{\sigma _{31}}}&{{\sigma _{32}}}&{\sigma _3^2} \end{array}} \right] Σ= σ12σ21σ31σ12σ22σ32σ13σ23σ32
其中指数部分展开为:
( x − μ x ) T ( Σ ) − 1 ( x − μ x ) = ( x − μ 1 ) 2 σ 1 2 + ( y − μ 2 ) 2 σ 2 2 + ( z − μ 3 ) 2 σ 3 2 − 2 σ 12 ( x − μ 1 ) ( y − μ 2 ) σ 1 σ 2 − 2 σ 13 ( x − μ 1 ) ( ( z − μ 3 ) ) σ 1 σ 3 − 2 σ 23 ( y − μ 2 ) ( ( z − μ 3 ) ) σ 2 σ 3 {\left( {x - {\mu _x}} \right)^T}{(\Sigma )^{ - 1}}\left( {x - {\mu _x}} \right) = \frac{{{{\left( {x - {\mu _1}} \right)}^2}}}{{\sigma _1^2}} + \frac{{{{\left( {y - {\mu _2}} \right)}^2}}}{{\sigma _2^2}} + \frac{{{{\left( {z - {\mu _3}} \right)}^2}}}{{\sigma _3^2}} - \frac{{2{\sigma _{12}}\left( {x - {\mu _1}} \right)\left( {y - {\mu _2}} \right)}}{{{\sigma _1}{\sigma _2}}} - \frac{{2{\sigma _{13}}\left( {x - {\mu _1}} \right)\left( {\left( {z - {\mu _3}} \right)} \right)}}{{{\sigma _1}{\sigma _3}}} - \frac{{2{\sigma _{23}}\left( {y - {\mu _2}} \right)\left( {\left( {z - {\mu _3}} \right)} \right)}}{{{\sigma _2}{\sigma _3}}} (x−μx)T(Σ)−1(x−μx)=σ12(x−μ1)2+σ22(y−μ2)2+σ32(z−μ3)2−σ1σ22σ12(x−μ1)(y−μ2)−σ1σ32σ13(x−μ1)((z−μ3))−σ2σ32σ23(y−μ2)((z−μ3))
因此,公式展开为:
f ( [ x , y , z ] ) = 1 ( 2 π ) 3 ∣ Σ ∣ 1 2 e − 1 2 [ ( x − μ 1 ) 2 σ 1 2 + ( y − μ 2 ) 2 σ 2 2 + ( z − μ 3 ) 2 σ 3 2 − 2 σ 12 ( x − μ 1 ) ( y − μ 2 ) σ 1 σ 2 − 2 σ 13 ( x − μ 1 ) ( ( z − μ 3 ) ) σ 1 σ 3 − 2 σ 23 ( y − μ 2 ) ( ( z − μ 3 ) ) σ 2 σ 3 ] f\left( {[x,y,z]} \right) = \frac{1}{{{{\left( {\sqrt {2\pi } } \right)}^3}{{\left| \Sigma \right|}^{\frac{1}{2}}}}}{e^{ - \frac{1}{2}\left[ {\frac{{{{\left( {x - {\mu _1}} \right)}^2}}}{{\sigma _1^2}} + \frac{{{{\left( {y - {\mu _2}} \right)}^2}}}{{\sigma _2^2}} + \frac{{{{\left( {z - {\mu _3}} \right)}^2}}}{{\sigma _3^2}} - \frac{{2{\sigma _{12}}\left( {x - {\mu _1}} \right)\left( {y - {\mu _2}} \right)}}{{{\sigma _1}{\sigma _2}}} - \frac{{2{\sigma _{13}}\left( {x - {\mu _1}} \right)\left( {\left( {z - {\mu _3}} \right)} \right)}}{{{\sigma _1}{\sigma _3}}} - \frac{{2{\sigma _{23}}\left( {y - {\mu _2}} \right)\left( {\left( {z - {\mu _3}} \right)} \right)}}{{{\sigma _2}{\sigma _3}}}} \right]}} f([x,y,z])=(2π )3∣Σ∣211e−21[σ12(x−μ1)2+σ22(y−μ2)2+σ32(z−μ3)2−σ1σ22σ12(x−μ1)(y−μ2)−σ1σ32σ13(x−μ1)((z−μ3))−σ2σ32σ23(y−μ2)((z−μ3))]
对于一个确定的三维高斯函数,其概率密度函数的取值范围是有限的,最大值出现在均值点 x = μ {\rm{x = }}\mu x=μ,当 x x x远离 μ \mu μ时函数值趋近于0。因此对应的 ( x − μ x ) T ( Σ ) − 1 ( x − μ x ) {\left( {x - {\mu _x}} \right)^T}{(\Sigma )^{ - 1}}\left( {x - {\mu _x}} \right) (x−μx)T(Σ)−1(x−μx)取值范围也是从0到一个具体的、有限的数值。当 ( x − μ x ) T ( Σ ) − 1 ( x − μ x ) = c o n s t a n t {\left( {x - {\mu _x}} \right)^T}{(\Sigma )^{ - 1}}\left( {x - {\mu _x}} \right) = {\rm{constant }} (x−μx)T(Σ)−1(x−μx)=constant时,即在取值范围内随机取某个值 c o n s t a n t constant constant,可以定义某一个椭球面:
( x − μ 1 ) 2 σ 1 2 + ( y − μ 2 ) 2 σ 2 2 + ( z − μ 3 ) 2 σ 3 2 − 2 σ 12 ( x − μ 1 ) ( y − μ 2 ) σ 1 σ 2 − 2 σ 13 ( x − μ 1 ) ( ( z − μ 3 ) ) σ 1 σ 3 − 2 σ 23 ( y − μ 2 ) ( ( z − μ 3 ) ) σ 2 σ 3 = c o n s t a n t \frac{{{{\left( {x - {\mu _1}} \right)}^2}}}{{\sigma _1^2}} + \frac{{{{\left( {y - {\mu _2}} \right)}^2}}}{{\sigma _2^2}} + \frac{{{{\left( {z - {\mu _3}} \right)}^2}}}{{\sigma _3^2}} - \frac{{2{\sigma _{12}}\left( {x - {\mu _1}} \right)\left( {y - {\mu _2}} \right)}}{{{\sigma _1}{\sigma _2}}} - \frac{{2{\sigma _{13}}\left( {x - {\mu _1}} \right)\left( {\left( {z - {\mu _3}} \right)} \right)}}{{{\sigma _1}{\sigma _3}}} - \frac{{2{\sigma _{23}}\left( {y - {\mu _2}} \right)\left( {\left( {z - {\mu _3}} \right)} \right)}}{{{\sigma _2}{\sigma _3}}} = {\rm{constant}} σ12(x−μ1)2+σ22(y−μ2)2+σ32(z−μ3)2−σ1σ22σ12(x−μ1)(y−μ2)−σ1σ32σ13(x−μ1)((z−μ3))−σ2σ32σ23(y−μ2)((z−μ3))=constant
因为展开整理,可以得到椭圆的一般二次形式:
A x 2 + B y 2 + C z 2 + D x y + E x z + F y z + + G x + H y + I z + J = 0 A{{\rm{x}}^2} + B{y^2} + C{z^2} + Dxy + Exz + Fyz + + Gx + Hy + Iz + J = 0 Ax2+By2+Cz2+Dxy+Exz+Fyz++Gx+Hy+Iz+J=0
因此 ( x − μ x ) T ( Σ ) − 1 ( x − μ x ) {\left( {x - {\mu _x}} \right)^T}{(\Sigma )^{ - 1}}\left( {x - {\mu _x}} \right) (x−μx)T(Σ)−1(x−μx)在其取值范围内可以构成无数个椭圆面,大椭球面套小椭球面,共同组成了一个实心椭球。每个椭圆面都可以计算出对应的概论密度值 f ( [ x , y , z ] ) = c o n s t a n t f\left( {[x,y,z]} \right) = {\rm{constant}} f([x,y,z])=constant,即椭球面上的所有坐标点的概论密度值。
各向同性(Isotropic)和各向异性(Anisotropic)
进一步深入探讨各向同性和 各向异性在 3D高斯分布中的数学形式以及几何表现。
各向同性高斯分布: 指在所有方向上具有相同的性质,数据在各个方向上的扩展程度(方差)相同,协方差为0,协方差矩阵:
Σ = [ σ 2 0 0 0 σ 2 0 0 0 σ 2 ] \Sigma = \left[ {\begin{array}{c} {{\sigma ^2}}&0&0\\ 0&{{\sigma ^2}}&0\\ 0&0&{{\sigma ^2}} \end{array}} \right] Σ= σ2000σ2000σ2
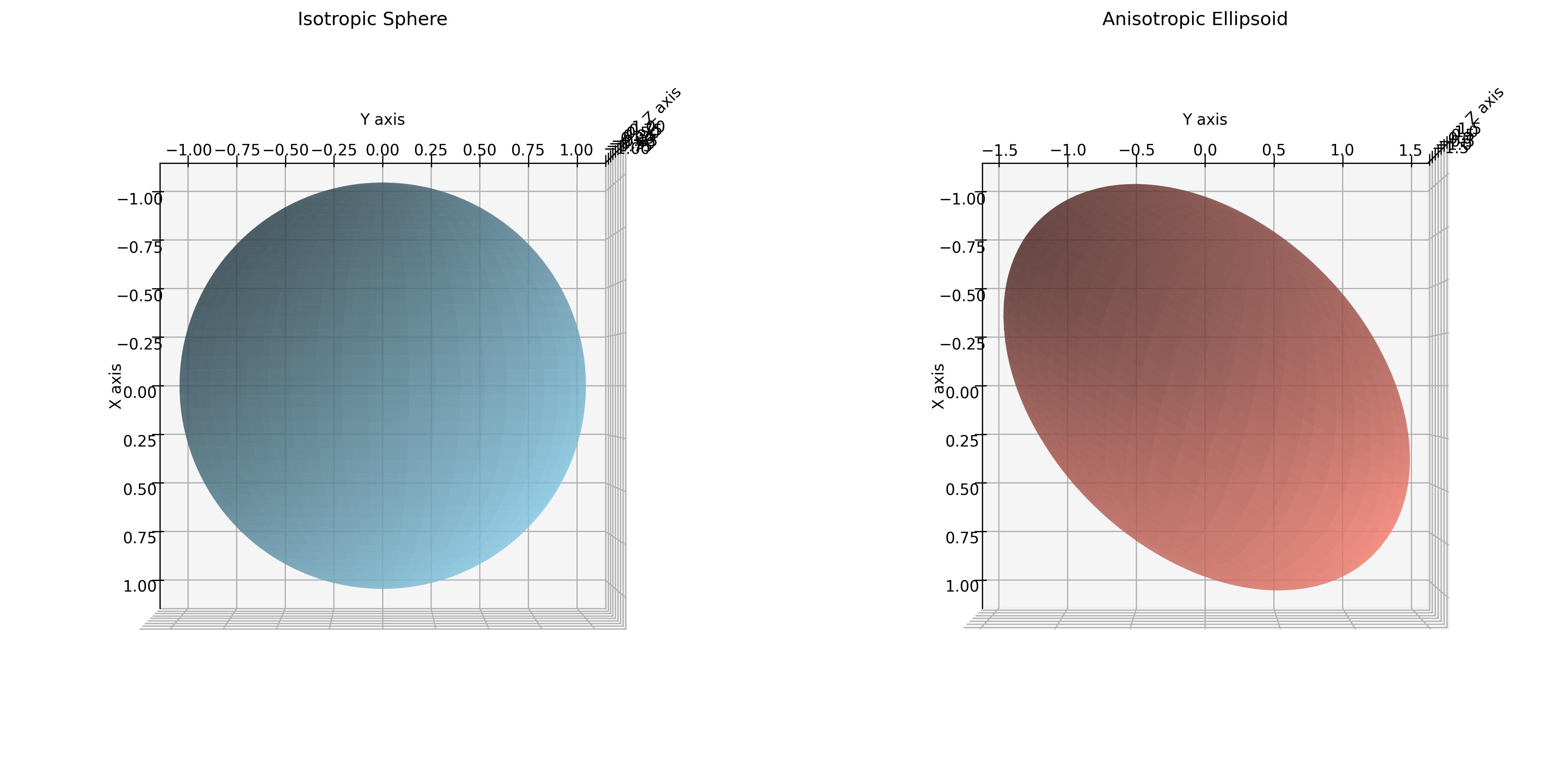
三个维度之间无相关性(协方差为0),且方差一致。 对应的高斯分布在三维空间中呈现为一个球形。
各向异性高斯分布: 表示在不同方向上性质不同,数据在不同方向上的扩展程度(方差)不同,协方差可能不为0,协方差矩阵更一般化:
Σ = [ σ 1 2 σ 12 σ 13 σ 21 σ 2 2 σ 23 σ 31 σ 32 σ 3 2 ] \Sigma = \left[ {\begin{array}{c} {\sigma _1^2}&{{\sigma _{12}}}&{{\sigma _{13}}}\\ {{\sigma _{21}}}&{\sigma _2^2}&{{\sigma _{23}}}\\ {{\sigma _{31}}}&{{\sigma _{32}}}&{\sigma _3^2} \end{array}} \right] Σ= σ12σ21σ31σ12σ22σ32σ13σ23σ32
三个维度之间可能有相关性(协方差不为0),且方差互不一致。对应的高斯分布在三维空间中呈现为一个椭球体,即沿不同主轴方向拉伸或压缩。
python
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
def plot_ellipsoid(ax, mean, cov, color='blue', n_points=100):
"""
在给定的axes上绘制一个基于协方差矩阵的椭球。
"""
# 生成单位球面点
u = np.linspace(0, 2 * np.pi, n_points)
v = np.linspace(0, np.pi, n_points)
x = np.outer(np.cos(u), np.sin(v))
y = np.outer(np.sin(u), np.sin(v))
z = np.outer(np.ones_like(u), np.cos(v))
# 协方差矩阵特征分解
eigvals, eigvecs = np.linalg.eigh(cov)
# 按特征值大小排序(从大到小)
idx = np.argsort(eigvals)[::-1]
eigvals = eigvals[idx]
eigvecs = eigvecs[:, idx]
# 构建缩放矩阵
scale_matrix = np.diag(np.sqrt(eigvals)) # 取平方根得到标准差
# 将单位球变换为椭球
for i in range(len(x)):
points = np.column_stack([x[i], y[i], z[i]])
transformed = points @ (scale_matrix @ eigvecs.T) + mean
x[i], y[i], z[i] = transformed[:, 0], transformed[:, 1], transformed[:, 2]
# 绘制椭球
ax.plot_surface(x, y, z, color=color, alpha=0.6, linewidth=0, antialiased=True)
# 创建图形和子图
fig = plt.figure(figsize=(15, 7))
# 各向同性椭球(球体)
ax1 = fig.add_subplot(121, projection='3d')
mean_iso = [0, 0, 0]
cov_iso = np.eye(3)
plot_ellipsoid(ax1, mean_iso, cov_iso, color='skyblue')
# 设置坐标轴标签
ax1.set_xlabel('X axis')
ax1.set_ylabel('Y axis')
ax1.set_zlabel('Z axis')
ax1.set_title('Isotropic Sphere')
# 调整视角以正对Z轴
ax1.view_init(elev=90, azim=0)
# 各向异性椭球
ax2 = fig.add_subplot(122, projection='3d')
mean_aniso = [0, 0, 0]
cov_aniso = np.array([[1, 0.5, 0.3],
[0.5, 2, 0.4],
[0.3, 0.4, 3]])
plot_ellipsoid(ax2, mean_aniso, cov_aniso, color='salmon')
# 设置坐标轴标签
ax2.set_xlabel('X axis')
ax2.set_ylabel('Y axis')
ax2.set_zlabel('Z axis')
ax2.set_title('Anisotropic Ellipsoid')
# 调整视角以正对Z轴
ax2.view_init(elev=90, azim=0)
plt.tight_layout()
plt.savefig("gaussian_distribution_visualizer.jpg", dpi=300, bbox_inches='tight')
plt.show()总结
尽可能简单、详细的介绍了高斯椭球的形成原理。