目录
[计算dir1 dir2的夹角](#计算dir1 dir2的夹角)
[编辑 计算圆弧是否按照顺时针方向来绘制](#编辑 计算圆弧是否按照顺时针方向来绘制)
前言
圆弧使用 ArcCurve 绘制,那么需要以下参数

我们拿3个点制作一个圆弧

计算圆心坐标
由 p1 - p2和p3 - p2构成两个向量dir1 dir2 这三个点构成的两条线的方向,

计算两条直线的角平分线
dir1 dir2 向量相加得到两条向量的角平分线
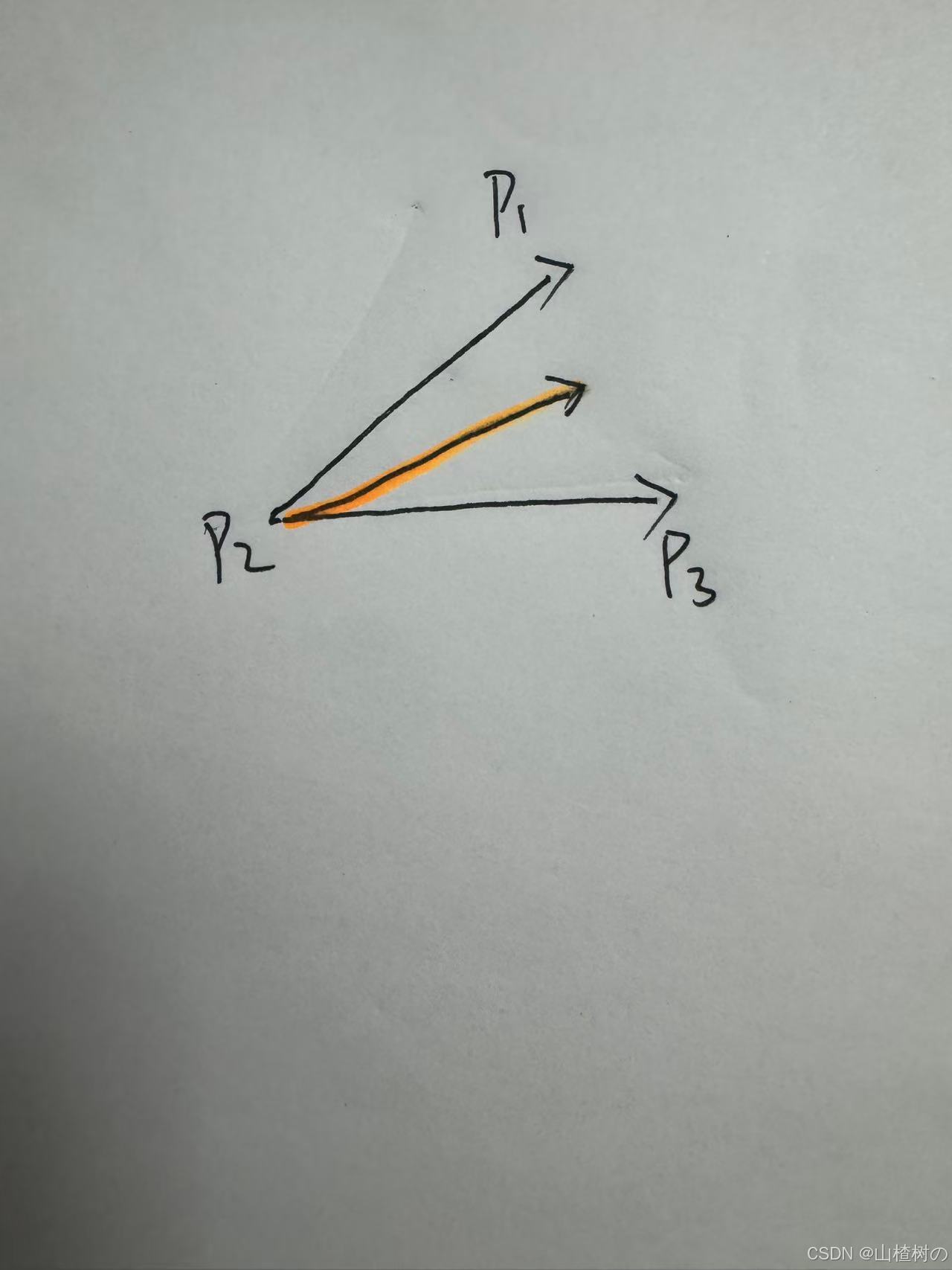

计算dir1 dir2的夹角
通过点乘计算两向量的余弦值,然后通过反余弦得到夹角

计算圆心到直线交点的距离
设圆弧半径为R,设圆心到直线交点距离为L,R = L * Sin(夹角/2) ==> L = R / Sin(夹角/2)
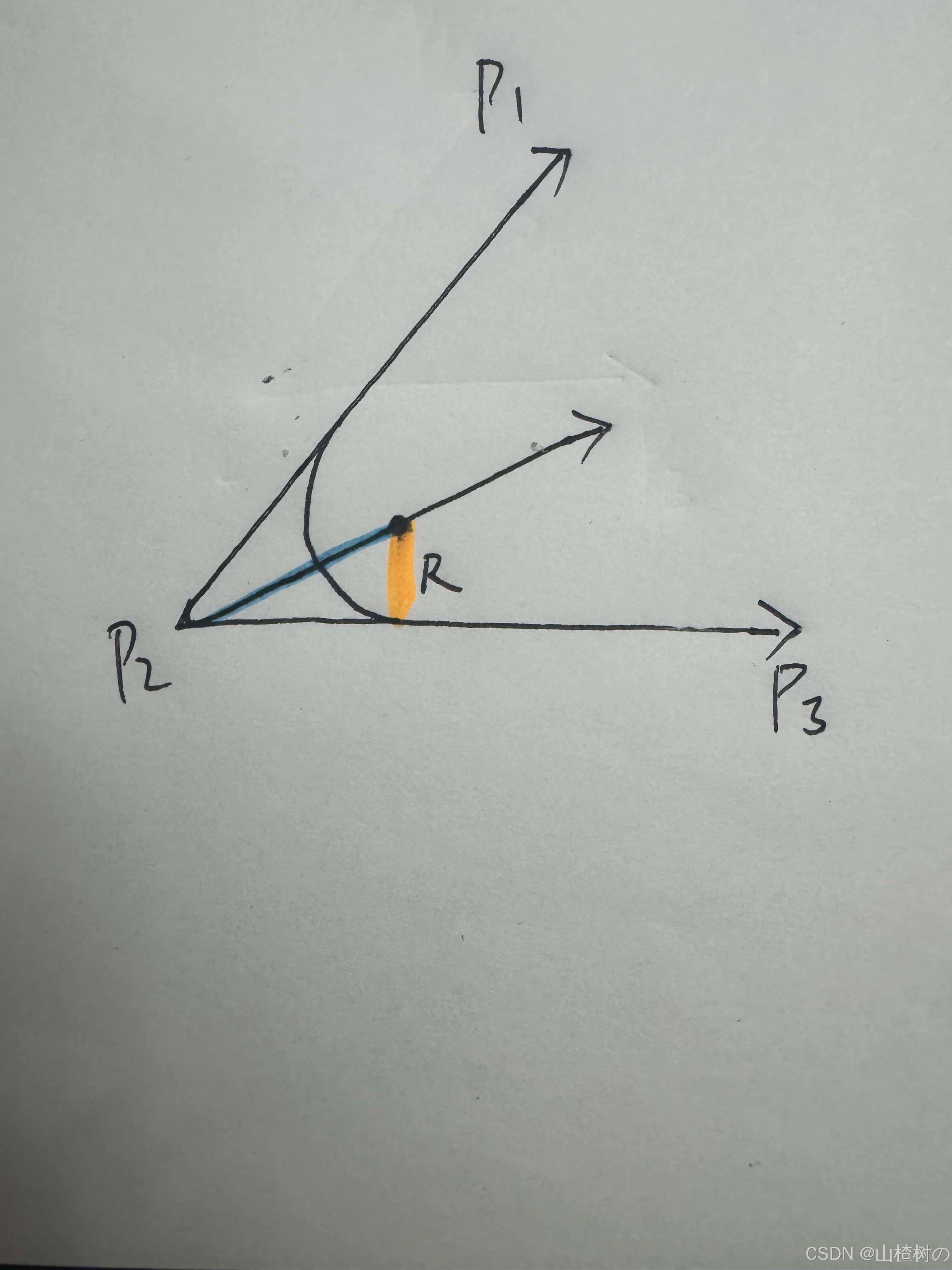
计算圆心
角平分线方向知道了,两向量交点到圆心的距离L知道了,那么圆心坐标就等于 起点+角平分线方向*L

计算从正X轴算起曲线开始、终止的角度
计算垂足与两直线交点距离

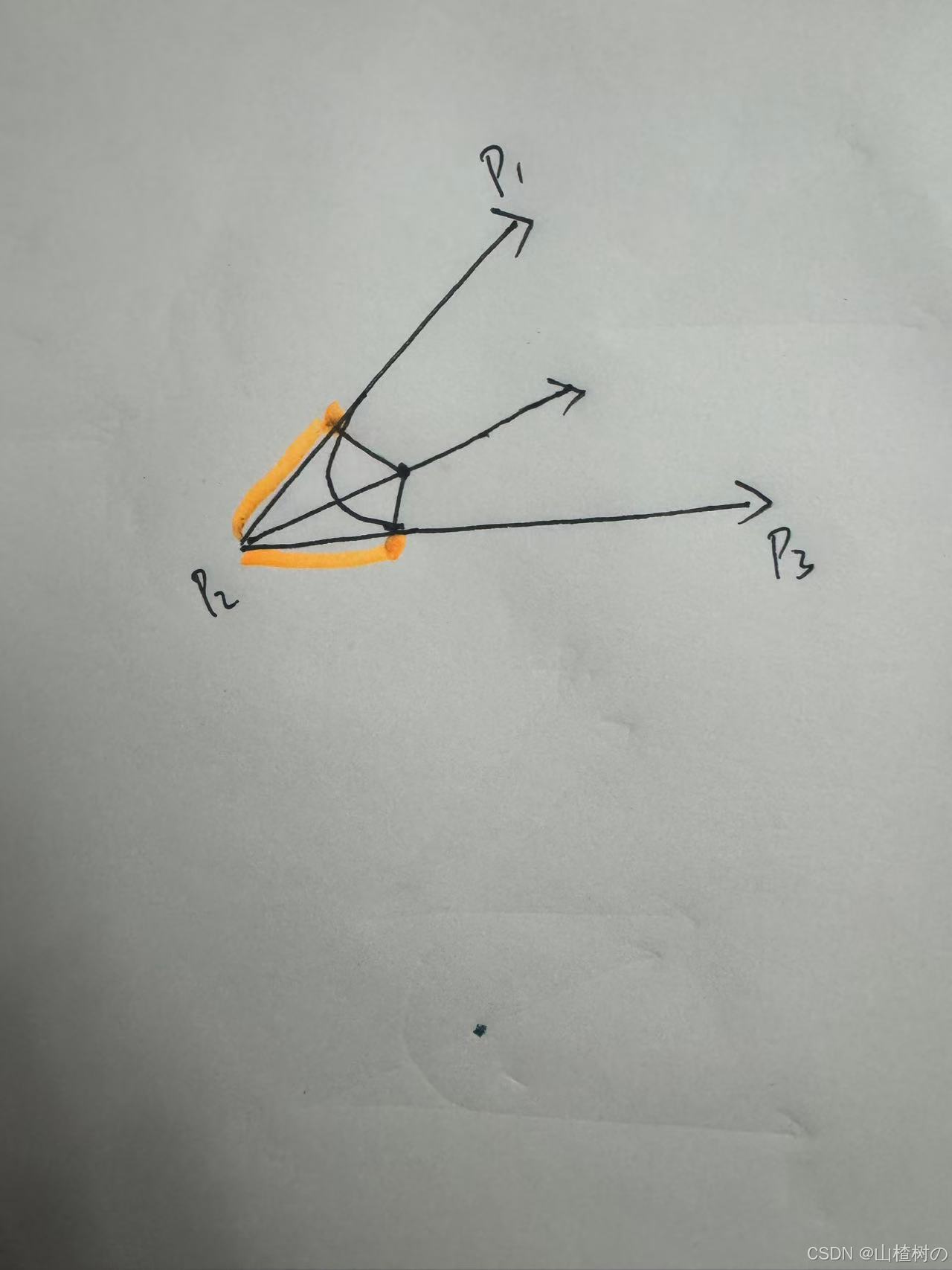
计算垂足
垂足向量等于p2起点+各方向*垂足到两直线交点距离

计算垂线

计算两垂线与x轴的夹角
设x轴向量为(1, 0, 0)。
这里需要注意点乘的操作是基于180度有效的,也就是余弦在180度内有效为一个周期,如果垂线的y小于0,需要一个圆周 减去 点乘所算的夹角,如下图示意,点乘算的是黑色弧度角,但真正的垂线与x轴夹角是彩色弧度
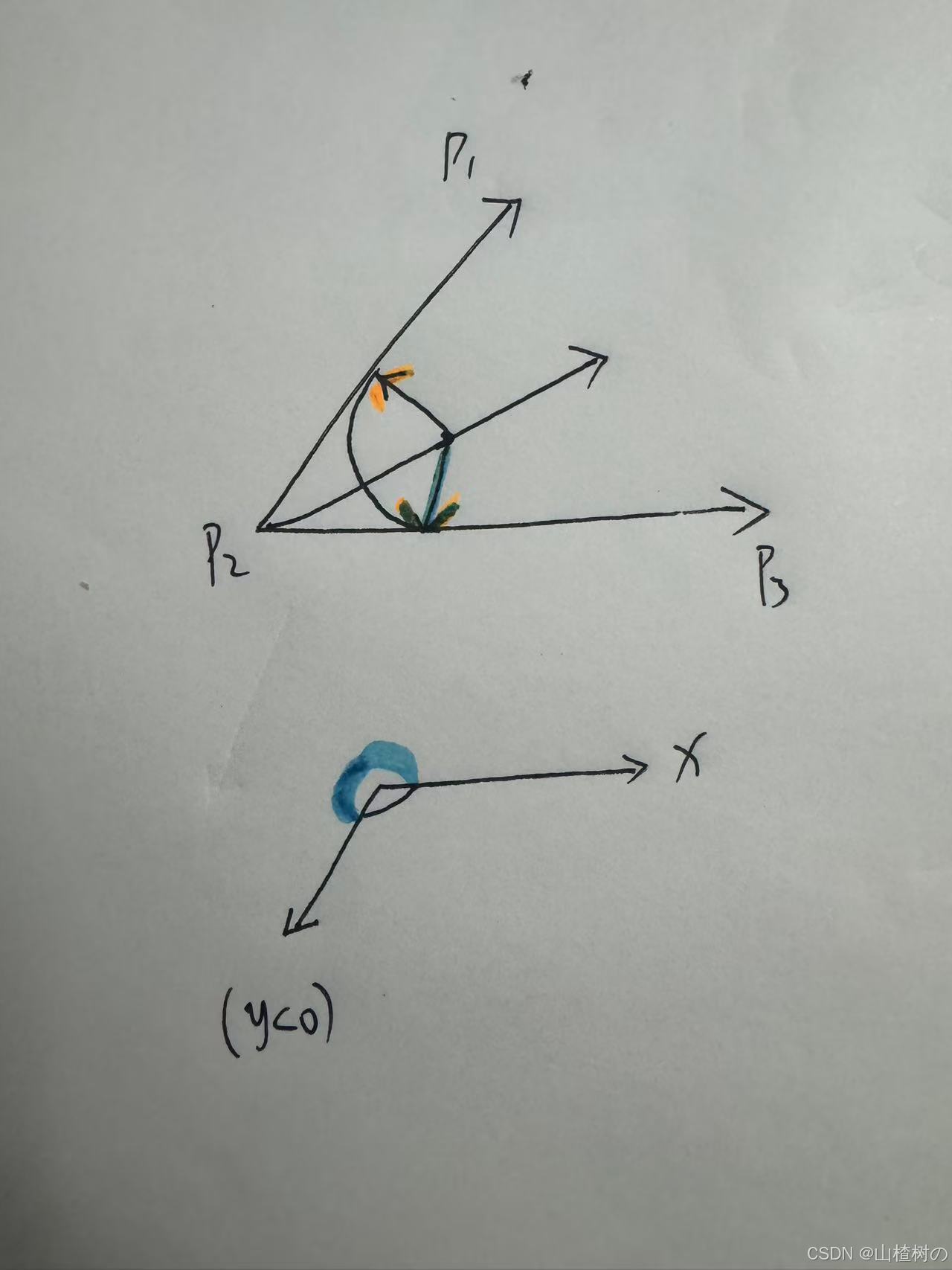
 计算圆弧是否按照顺时针方向来绘制
计算圆弧是否按照顺时针方向来绘制
根据WebGL右手螺旋定则,dir1 叉乘 dir2 得到的法线向量,判断这个向量的方向是否大于0

成功画弧线

多个圆弧的应用
逻辑和单个圆弧是一样的,需要注意的是,如果多个点之间并不存在弧度,就不需要做弧度处理,可以用两直线向量叉乘计算,如果叉乘结果是0向量(正弦值为0,两向量相反即夹角180度)则说明两条直线没有夹角。


