一、PCA思想
1.1 PCA定义
PCA（Principal Component Analysis，主成分分析）是一种统计学方法，用于对数据进行降维处 理 。它通过线性变换 将原始数据转换到一个新的坐标系统中，使得在这个新坐标系下，数据的方差 沿着坐标轴被最大化。PCA的目标是提取数据中最重要的信息（即主成分），同时去除冗余信息，从而降低数据的维度，同时保留数据的主要特征
1.2 主要思想
1.数据降维与特征提取
- 原始数据可能包含许多维度（特征），但并非所有维度都对数据的结构和信息有重要贡献。PCA通过寻找数据中的主要方向（主成分），将数据投影到这些方向上，从而减少数据的维度，同时保留数据的主要信息
- 例如，在一个二维数据集中，如果数据点主要沿着某个方向分布，PCA可以将数据投影到这个方向上，从而将二维数据降为一维
2.方差最大化
- PCA的核心是最大化数据在新坐标系中的方差。方差越大，数据在这个方向上的变化越显著，因此该方向被认为包含了更多的信息。PCA通过计算数据的协方差矩阵，找到其特征值和特征向量，特征值越大，对应的特征向量方向上的方差越大，这些特征向量即为主成分
- 具体来说，第一个主成分是数据方差最大的方向，第二个主成分是与第一个主成分正交且方差次大的方向，以此类推
3.去除冗余信息
- 原始数据中可能存在相关性较高的特征，这些特征包含重复或冗余的信息。PCA通过将数据投影到主成分方向上，去除这些冗余信息，使得降维后的数据特征之间相互独立。
- 例如，如果两个特征高度相关，PCA会将它们合并为一个主成分，从而减少数据的冗余
4.数据重构与信息损失
- PCA不仅用于降维，还可以用于数据重构。通过选择前k个主成分，可以将数据从高维空间映射到低维空间，然后再通过逆变换重构数据。虽然重构后的数据会丢失一些信息（即方差较小的主成分所对应的细节），但这些信息通常是不重要的，因此PCA在降维的同时尽量保留了数据的主要结构和特征
5.正交变换
- PCA的变换是正交变换，即新的坐标轴（主成分）之间相互正交。这意味着主成分之间没有相关性，每个主成分都独立地表示了数据的一个主要方向。这种正交性使得PCA在处理高维数据时非常有效，因为它可以清晰地分离出数据中的不同特征
二、PCA原理
2.1 数据预处理
在进行PCA之前，通常需要对数据进行预处理，主要包括以下两个步骤：
1.中心化（均值归零）
PCA要求数据的均值为零。因此，需要对每个特征减去其均值，使数据的中心移动到原点。具体来说，对于数据集
中的每个特征
这一步是为了确保PCA的目标是最大化数据的方差，而不是均值
2.标准化（可选）
如果数据的各个特征的量纲不同或方差差异较大，可以进一步对数据进行标准化，即对每个特征进行缩放，使其标准差为1。标准化的公式为：
其中
2.2 计算协方差矩阵
PCA的核心是通过协方差矩阵来衡量数据中各特征之间的相关性。协方差矩阵是一个对称矩阵，其对角线元素表示各特征的方差，非对角线元素表示特征之间的协方差。对于中心化后的数据矩阵
其中，
2.3 特征值分解
PCA的目标是找到一组新的坐标轴（主成分），使得数据在这些坐标轴上的方差最大化。这些坐标轴的方向由协方差矩阵的特征向量决定，而特征值则表示数据在这些方向上的方差大小
- 特征值和特征向量的计算： 对协方差矩阵
- **特征值的排序：**将特征值按照从大到小的顺序排列，对应的特征向量即为数据的主成分。第一个主成分对应最大的特征值，表示数据方差最大的方向；第二个主成分对应次大的特征值，表示与第一个主成分正交且方差次大的方向，依此类推
2.4 选择主成分
根据特征值的大小，选择前 k 个主成分，其中 k < d 。这些主成分构成了新的特征空间，用于降维后的数据表示。通常，选择的主成分数量 k 会根据累计方差贡献率来确定，即选择足够多的主成分，使得它们的方差贡献率达到一个较高的比例（如95%）
累计方差贡献率：计算前 k 个主成分的累计方差贡献率：
选择 k 使得累计方差贡献率接近1，表示保留了大部分数据的方差信息
2.5 数据投影
将原始数据投影到选定的主成分方向上，得到降维后的数据。具体来说，设前 k 个主成分对应的特征向量构成矩阵
其中，Y 是降维后的数据矩阵，其维度为 n * k
三、PCA实验
3.1 代码实现
python
import numpy as np
import os
from PIL import Image
import matplotlib.pyplot as plt
# 1. 加载ORL_Faces数据集
def load_images(base_path):
data = []
labels = []
image_paths = [] # 保存图片路径以便后续显示
if not os.path.exists(base_path):
raise FileNotFoundError(f"数据集目录不存在: {base_path}")
print(f"正在查找数据集: {base_path}")
for i in range(1, 41): # s1 to s40
folder = os.path.join(base_path, f's{i}')
if not os.path.exists(folder):
print(f"警告: 子文件夹不存在，跳过: {folder}")
continue
print(f"正在处理文件夹: {folder}")
for filename in os.listdir(folder):
if filename.endswith('.pgm'):
img_path = os.path.join(folder, filename)
try:
img = Image.open(img_path).convert('L') # 转换为灰度图
img_array = np.array(img).flatten() # 展平为一维向量
data.append(img_array)
labels.append(i) # 记录类别
image_paths.append(img_path) # 记录图片路径
except Exception as e:
print(f"加载图片 {img_path} 出错: {e}")
if not data:
raise ValueError("未找到任何有效的 .pgm 图片。")
return np.array(data), np.array(labels), image_paths
# 2. 手动实现PCA
def manual_pca(X, n_components):
# 标准化数据
X_mean = np.mean(X, axis=0)
X_std = np.std(X, axis=0)
X_std_data = (X - X_mean) / X_std
# 计算协方差矩阵
cov_matrix = np.cov(X_std_data.T)
# 特征值分解
eigenvalues, eigenvectors = np.linalg.eigh(cov_matrix)
# 按特征值从大到小排序
idx = np.argsort(eigenvalues)[::-1]
eigenvalues = eigenvalues[idx]
eigenvectors = eigenvectors[:, idx]
# 计算解释方差比
explained_variance_ratio = eigenvalues / np.sum(eigenvalues)
print(f"解释方差比: {np.sum(explained_variance_ratio[:n_components]):.4f}")
# 选择前n_components个特征向量
selected_vectors = eigenvectors[:, :n_components]
# 投影到主成分空间
X_pca = np.dot(X_std_data, selected_vectors)
# 返回重建所需的数据
return X_pca, selected_vectors, X_mean, X_std, explained_variance_ratio
# 3. 可视化原始和重建图片
def visualize_reconstruction(original_data, reconstructed_data, image_paths, img_shape, num_samples=5):
# 随机选择 num_samples 张图片
indices = np.random.choice(original_data.shape[0], num_samples, replace=False)
# 设置支持中文的字体
plt.rcParams['font.sans-serif'] = ['SimHei'] # 使用黑体
plt.rcParams['axes.unicode_minus'] = False # 解决负号显示问题
# 创建子图
fig, axes = plt.subplots(num_samples, 2, figsize=(8, num_samples * 4))
if num_samples == 1:
axes = [axes] # 确保单张图片时 axes 可迭代
for i, idx in enumerate(indices):
# 原始图片
original_img = original_data[idx].reshape(img_shape)
axes[i, 0].imshow(original_img, cmap='gray')
axes[i, 0].set_title(f'原始图片 (ID: {idx})')
axes[i, 0].axis('off')
# 重建图片
reconstructed_img = reconstructed_data[idx].reshape(img_shape)
axes[i, 1].imshow(reconstructed_img, cmap='gray')
axes[i, 1].set_title(f'PCA 重建图片 (ID: {idx})')
axes[i, 1].axis('off')
plt.suptitle('原始图片与 PCA 重建图片对比')
plt.tight_layout(rect=[0, 0, 1, 0.95])
plt.show()
# 4. 主程序
def main():
# 数据集路径
base_path = '文件路径' # 请确认实际路径
try:
X, y, image_paths = load_images(base_path)
except Exception as e:
print(f"加载图片失败: {e}")
return
# 保存原始数据和图片尺寸
X_original = X.copy()
img_shape = (112, 92) # ORL Faces 图片尺寸，通常为 112x92
# 应用手动PCA
n_components = 50 # 降维后的维度
X_pca, selected_vectors, X_mean, X_std, explained_variance = manual_pca(X, n_components)
# 重建数据
X_reconstructed = np.dot(X_pca, selected_vectors.T) # 逆投影
X_reconstructed = X_reconstructed * X_std + X_mean # 恢复标准化前的尺度
# 设置支持中文的字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 可视化前两个主成分
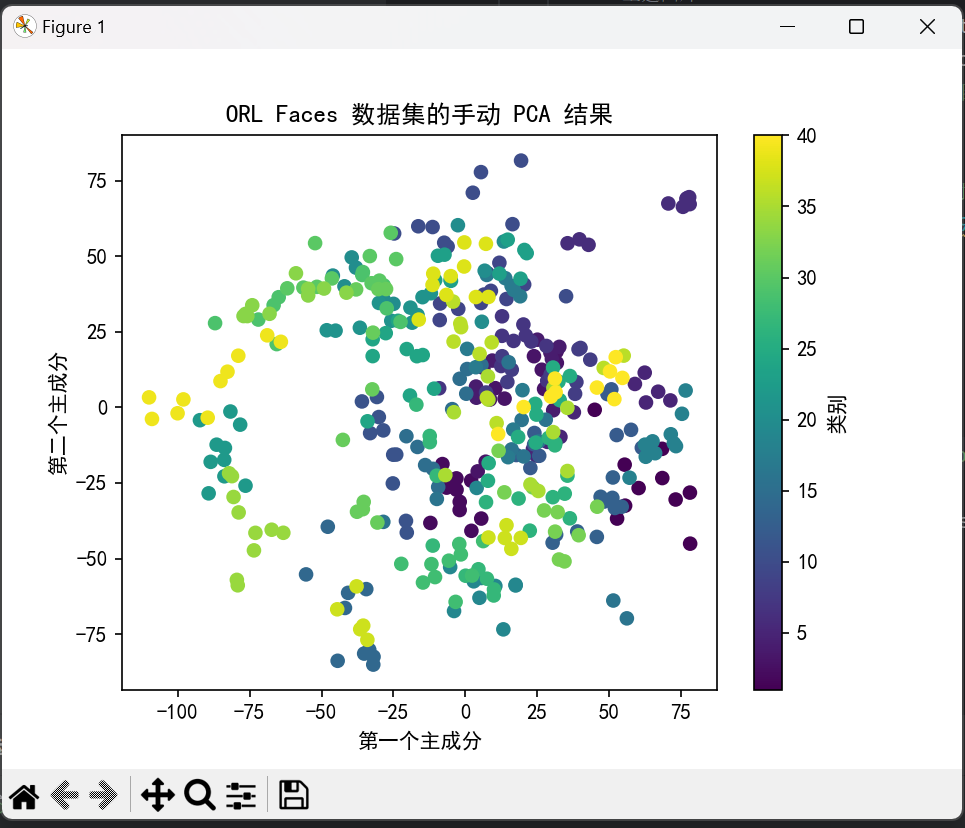
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y, cmap='viridis')
plt.xlabel('第一个主成分')
plt.ylabel('第二个主成分')
plt.title('ORL Faces 数据集的手动 PCA 结果')
plt.colorbar(label='类别')
plt.show()
# 可视化原始和重建图片
visualize_reconstruction(X_original, X_reconstructed, image_paths, img_shape, num_samples=5)
# 保存降维后的数据
np.save('X_pca_manual.npy', X_pca)
if __name__ == '__main__':
main()3.2 实验效果截图
1.代码运行截图
2.数据集手动PCA结果图像显示截图
3.PCA重建图片与原图对比截图
四、实验总结
本次PCA实验在ORL Faces数据集上取得了以下效果：
- 成功地将高维数据投影到二维空间，并通过可视化展示了数据的分布情况
- 通过PCA重建的图像在保留主要特征的同时实现了数据压缩
- 较高的解释方差比表明选择的主成分能够有效地捕捉数据的主要变化
这些结果表明PCA是一种有效的降维和特征提取方法，可以用于图像处理和模式识别等领域。然而，需要注意的是，尽管PCA能够保留数据的主要特征，但在某些情况下可能会丢失一些细节信息，因此在实际应用中需要根据具体需求权衡降维的效果和信息损失