高等数学基础(行列式和矩阵的秩)

行列式主要用于判断矩阵是否可逆及计算特征方程

初见行列式

行列式起源于线性方程组求解
{ a 11 x 1 + a 12 x 2 = b 1 a 21 x 1 + a 22 x 2 = b 2 \begin{cases} a_{11}x_1 + a_{12}x_2 = b_1 \\ a_{21}x_1 + a_{22}x_2 = b_2 \end{cases} {a11x1+a12x2=b1a21x1+a22x2=b2

通过消元法得到, { ( a 11 a 22 − a 12 a 21 ) x 1 = b 1 a 22 − b 2 a 12 ( a 11 a 22 − a 12 a 21 ) x 2 = b 2 a 11 − b 1 a 21 \begin{cases} (a_{11}a_{22} - a_{12}a_{21})x_1 = b_1a_{22} - b_2a_{12} \\ (a_{11}a_{22} - a_{12}a_{21})x_2 = b_2a_{11} - b_1a_{21} \end{cases} {(a11a22−a12a21)x1=b1a22−b2a12(a11a22−a12a21)x2=b2a11−b1a21

当 a 11 a 22 − a 12 a 21 ≠ 0 a_{11}a_{22} - a_{12}a_{21} \ne 0 a11a22−a12a21=0时, 方程有唯一解
x 1 = b 1 a 22 − b 2 a 12 a 11 a 22 − a 12 a 21 , x 2 = b 2 a 11 − b 1 a 21 a 11 a 22 − a 12 a 21 x_1 = \frac{b_1a_{22} - b_2a_{12}}{a_{11}a_{22} - a_{12}a_{21}}, x_2 = \frac{b_2a_{11} - b_1a_{21}}{a_{11}a_{22} - a_{12}a_{21}} x1=a11a22−a12a21b1a22−b2a12,x2=a11a22−a12a21b2a11−b1a21

在方程组解的表达式中, 分母是方程组的4个系数确定, 提取4个系数并按他们在方程组中的位置, 排列为二行二列的数表(横排称为行, 竖排称为列)
a 11 a 12 a 21 a 22 \begin{matrix}a_{11} & a_{12} \\ a_{21} & a_{22}\end{matrix} a11a21a12a22, 其中 a 11 a 22 − a 12 a 21 a_{11}a_{22}-a_{12}a_{21} a11a22−a12a21表示为 [ a 11 a 12 a 21 a 22 ] \left[\begin{matrix}a_{11} & a_{12} \\ a_{21} & a_{22}\end{matrix}\right] [a11a21a12a22], 称为二阶行列式

利用二阶行列式, 方程组的解可以表示为 x 1 = D 1 D x_1 = \frac{D_1}{D} x1=DD1, x 2 = D 2 D x_2=\frac{D_2}{D} x2=DD2, 其中 D = [ a 11 a 12 a 21 a 22 ] D = \left[\begin{matrix}a_{11} & a_{12} \\ a_{21} & a_{22}\end{matrix}\right] D=[a11a21a12a22]称为系数行列式 D 1 = [ b 1 a 12 b 2 a 22 ] D_1 = \left[\begin{matrix}b_1 & a_{12} \\ b_2 & a_{22} \end{matrix}\right] D1=[b1b2a12a22], D 2 = [ a 11 b 1 a 21 b 2 ] D_2 = \left[\begin{matrix}a_{11} & b_1 \\ a_{21} & b_2 \end{matrix}\right] D2=[a11a21b1b2]

行列式定义

从二阶行列式推导到 n n n阶行列式的定义

a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋮ a n 1 a n 2 ⋯ a n n \] = ∑ j 1 j 2 . . . j n ( − 1 ) l a 1 j 1 a 2 j 2 ⋯ a n j n \\left\[\\begin{matrix} a_{11} \& a_{12} \& \\cdots \& a_{1n} \\\\ a_{21} \& a_{22} \& \\cdots \& a_{2n} \\\\ \\vdots \& \\vdots \& \& \\vdots \\\\ a_{n1} \& a_{n2} \& \\cdots \& a_{nn} \\end{matrix}\\right\] = \\sum_{j_1j_2...j_n}(-1)\^la_{1j_1}a_{2j_2}\\cdots a_{nj_n} a11a21⋮an1a12a22⋮an2⋯⋯⋯a1na2n⋮ann =j1j2...jn∑(−1)la1j1a2j2⋯anjn 其中 a i j a_{ij} aij, i = 1 , 2 ⋯   , n i=1,2\\cdots, n i=1,2⋯,n, j = 1 , 2 , ⋯   , n j=1,2,\\cdots, n j=1,2,⋯,n, 称为行列式的元素, 其中 i i i称为行标, 表示该元素位于哪一行, j j j称为列下表, 表示该元素位于哪一列 j 1 j 2 ⋯ j n j_1j_2\\cdots j_n j1j2⋯jn代表 ∑ j 1 j 2 . . . j n \\sum_{j_1j_2...j_n} ∑j1j2...jn对 j 1 j 2 ⋯ j n j_1j_2\\cdots j_n j1j2⋯jn取一遍 1 , 2 , ⋯ n 1,2,\\cdots n 1,2,⋯n的一切排列求和, 共有 n ! n! n!项 如, 123的排列为 123 , 132 , 213 , 232 , 312 , 321 123, 132, 213, 232, 312, 321 123,132,213,232,312,321排列 321 321 321的逆序数为 3 3 3, 3 ! = 6 3!=6 3!=6项 ##### 常见行列式计算 **一阶行列式** \[ a 1 \] = a 1 \\left\[\\begin{matrix} a_1 \\end{matrix}\\right\] = a_1 \[a1\]=a1 **二阶行列式** \[ a 11 a 12 a 21 a 22 \] = a 11 a 22 − a 12 a 21 \\left\[\\begin{matrix} a_{11} \& a_{12} \\\\ a_{21} \& a_{22} \\end{matrix}\\right\] = a_{11}a_{22} - a_{12}a_{21} \[a11a21a12a22\]=a11a22−a12a21 **三阶行列式** \[ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 \] = a 11 a 22 a 33 + a 12 a 23 a 31 + a 13 a 21 a 32 − a 13 a 22 a 31 − a 12 a 21 a 33 − a 11 a 23 a 32 \\left\[\\begin{matrix} a_{11} \& a_{12} \& a_{13} \\\\ a_{21} \& a_{22} \& a_{23} \\\\ a_{31} \& a_{32} \& a_{33} \\end{matrix}\\right\] = a_{11}a_{22}a_{33} + a_{12}a_{23}a_{31} + a_{13}a_{21}a_{32} - a_{13}a_{22}a_{31} - a_{12}a_{21}a_{33} - a_{11}a_{23}a_{32} a11a21a31a12a22a32a13a23a33 =a11a22a33+a12a23a31+a13a21a32−a13a22a31−a12a21a33−a11a23a32 **计算公式** 主对角线 - 副对角线 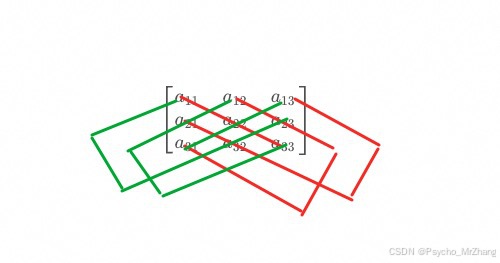![在这里插入图片描述](https://i-blog.csdnimg.cn/direct/788b12394d9d4f88bf8cacabbd100698.jpeg) **求行列式的值** A = \[ 1 − 2 3 − 1 2 1 − 3 − 4 − 2 \] A = \\left\[\\begin{matrix} 1 \& -2 \& 3 \\\\ -1 \& 2 \& 1 \\\\ -3 \& -4 \& -2 \\end{matrix}\\right\] A= 1−1−3−22−431−2 根据定义解得: A = 1 × 2 × ( − 2 ) + ( − 2 ) × 1 × ( − 3 ) + 3 × ( − 4 ) × ( − 1 ) − 3 × 2 × ( − 3 ) − ( − 2 ) × ( − 1 ) × ( − 2 ) − 1 × ( − 4 ) × 1 = 40 A=1 \\times 2 \\times (-2) + (-2) \\times 1 \\times (-3) + 3 \\times (-4) \\times (-1) - 3 \\times 2 \\times (-3) - (-2) \\times (-1) \\times (-2) - 1 \\times (-4) \\times 1 = 40 A=1×2×(−2)+(−2)×1×(−3)+3×(−4)×(−1)−3×2×(−3)−(−2)×(−1)×(−2)−1×(−4)×1=40 方阵 A A A的行列式可以判断 A A A是否可逆, **不为0可逆, 为0不可逆** #### 行列式和矩阵的区别 ##### 行列式 * 行数等于列数 * 共有 n 2 n\^2 n2个元素 * 本质是一个数值(一种矩阵的计算方式) ##### 矩阵 * 行数可以不等于列数 * 有 m × n m \\times n m×n和元素 * 本质是一个数表 #### 行列式计算 `Numpy`中通过`np.linalg.det()`函数计算 ```python import numpy as np A = np.array([[1, 2], [3, 4]]) print("A 的行列式为 np.linalg.det(A): ", np.linalg.det(A)) print("A 矩阵是否可逆: ", np.linalg.det(A) != 0) B = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) print("B 的行列式为 np.linalg.det(B): ", np.linalg.det(B)) print("B 矩阵是否可逆: ", np.linalg.det(B) != 0) ``` ### 矩阵的秩 矩阵的秩代表计算线性方程组解的数目, 去掉无关项(线性相关)然后其余的数量就是矩阵的秩, 矩阵的秩可以从行和列两个方向观察, 首先要了解线性相关和线性无关 #### 向量组 α 1 = \[ a 11 a 21 ⋮ a m 1 \] , α 2 = \[ a 12 a 22 ⋮ a m 2 \] , α n = \[ a 1 n a 2 n ⋮ a m n \] \\alpha_1 = \\left\[\\begin{matrix} a_{11} \\\\ a_{21} \\\\ \\vdots \\\\ a_{m1} \\end{matrix}\\right\], \\alpha_2 = \\left\[\\begin{matrix} a_{12} \\\\ a_{22} \\\\ \\vdots \\\\ a_{m2} \\end{matrix}\\right\], \\alpha_n = \\left\[\\begin{matrix} a_{1n} \\\\ a_{2n} \\\\ \\vdots \\\\ a_{mn} \\end{matrix}\\right\] α1= a11a21⋮am1 ,α2= a12a22⋮am2 ,αn= a1na2n⋮amn , 每个 α i \\alpha_i αi称为 m m m维列向量 β 1 = \[ a 11 a 21 ⋯ a m 1 \] , β 2 = \[ a 12 a 22 ⋯ a m 2 \] , β n = \[ a 1 n a 2 n ⋯ a m n \] \\beta_1 = \\left\[\\begin{matrix} a_{11} \& a_{21} \& \\cdots \& a_{m1} \\end{matrix}\\right\], \\beta_2 = \\left\[\\begin{matrix} a_{12} \& a_{22} \& \\cdots \&\& a_{m2} \\end{matrix}\\right\], \\beta_n = \\left\[\\begin{matrix} a_{1n} \& a_{2n} \& \\cdots \& a_{mn} \\end{matrix}\\right\] β1=\[a11a21⋯am1\],β2=\[a12a22⋯am2\],βn=\[a1na2n⋯amn\], 每个 a i a_i ai称为 m m m维行向量 ```python import numpy as np A = np.array([[1, 2, 3], [4, 5, 6]]) # reshape 重新绘制向量, 否则为1维数组 print("第0行: \n", A[0, :].reshape(1, -1)) print("第1列: \n", A[:, 1].reshape(-1, 1)) """output: 第0行: [[1 2 3]] 第1列: [[2] [5]] """ ``` #### 向量组的线性相关和线性无关 ##### 线性相关 vs 线性无关 **本质问题**：这些向量里有没有「多余的」？ ###### 线性相关（有冗余） * **例子** ： 向量A = \[1,2\]，向量B = \[2,4

→ B = 2×A，B完全可以用A复制粘贴得到

→ 像拼乐高时，你已经有红砖了，又拿了个两倍大的红砖，没带来新形状

数学定义 ：

存在不全为0的系数（比如k₁=2, k₂=-1），使得 k₁A + k₂B = 0

→ 向量之间能互相「组合」出来，存在冗余

线性无关（都必要）

例子：

向量X = [1,0]（横向箭头），向量Y = [0,1]（纵向箭头）

→ 无法用X造出Y，也无法用Y造出X

→ 像乐高红砖和蓝砖，拼平面必须同时需要两者
数学意义 ：

没有任何一个向量能被其他向量组合出来

→ 每个向量都贡献了独特的「方向」

矩阵的秩（本质：独立信息数）

本质问题：这个矩阵里有多少个真正「有用」的向量？

直观理解

矩阵就像行李箱打包 ：
每一列是一个物品（向量），秩 = 真正有用的物品数量
- 如果塞了5件衣服但都是同样的T恤 → 秩=1（其实带一件就够了）
- 如果带了T恤、外套、裤子、袜子 → 秩=4（每样都不同）

具体例子

秩=1的矩阵：
复制代码
```
[1 2 3]  
[2 4 6]  
```
→ 所有列都是[1,2]的倍数，第三列=第一列×3

→ 像只带了一个U盘但复制了3份文件，实际信息量=1
秩=2的矩阵：
复制代码
```
[1 0 1]  
[0 1 1]  
```
→ 前两列是X/Y方向箭头，第三列=前两列相加

→ 虽然3列，但最多能表示二维平面里的所有点

几何意义

秩=能撑开的空间维度
- 秩1 → 所有向量挤在一条直线上
- 秩2 → 向量铺满一个平面
- 秩3（三维矩阵）→ 充满立体空间

为什么重要？

解方程 ：

Ax=0的解的数量 = 未知数个数 - 秩

→ 秩越小，自由度越大（比如行李箱空位多）
数据压缩 ：

图片/视频矩阵如果秩低，说明有大量重复 → 可压缩
机器学习 ：

特征向量如果线性相关，说明有冗余特征需要剔除

矩阵秩的计算

题目1：

求矩阵 A = [ 1 2 3 2 4 6 3 6 9 ] A = \begin{bmatrix} 1 & 2 & 3 \\ 2 & 4 & 6 \\ 3 & 6 & 9 \end{bmatrix} A= 123246369 的秩。

步骤解析：

观察原始矩阵 ：

每一行的数字都很像成比例的：
- 第2行 = 第1行 × 2
- 第3行 = 第1行 × 3
  → 明显冗余（像行李箱里塞了3个同样的T恤）。
用行变换化简 ：

目标是把矩阵变成「阶梯形」，只保留独立信息。
- 第1步 ：保留第1行不变。
  1 2 3 2 4 6 3 6 9 \] \\begin{bmatrix} 1 \& 2 \& 3 \\\\ 2 \& 4 \& 6 \\\\ 3 \& 6 \& 9 \\end{bmatrix} 123246369
  - 第2行 → 第2行 - 2×第1行： $2 , 4 , 6 \] − 2 × \[ 1 , 2 , 3 \] = \[ 0 , 0 , 0 \] \[2, 4, 6\] - 2×\[1, 2, 3\] = \[0, 0, 0\] \[2,4,6\]−2×\[1,2,3\]=\[0,0,0$
  - 第3行 → 第3行 - 3×第1行： $3 , 6 , 9 \] − 3 × \[ 1 , 2 , 3 \] = \[ 0 , 0 , 0 \] \[3, 6, 9\] - 3×\[1, 2, 3\] = \[0, 0, 0\] \[3,6,9\]−3×\[1,2,3\]=\[0,0,0$ 结果变为： $1 2 3 0 0 0 0 0 0 \] \\begin{bmatrix} 1 \& 2 \& 3 \\\\ 0 \& 0 \& 0 \\\\ 0 \& 0 \& 0 \\end{bmatrix} 100200300$
只有第1行是非零行 → 秩 = 1。

比喻解释：

矩阵像一个行李箱，里面装了3件物品（3行），但全是同一款T恤（成比例）。
实际有用的物品只有1件 → 秩 = 1。

题目2：

求矩阵 B = [ 1 0 2 0 1 3 ] B = \begin{bmatrix} 1 & 0 & 2 \\ 0 & 1 & 3 \end{bmatrix} B=[100123] 的秩。

步骤解析：

观察原始矩阵：
- 第1行和第2行没有比例关系（像一件T恤和一条裤子）。
- 已经是阶梯形（每行的首项数字在右侧）。
直接统计非零行数 ：

有2行非零行 → 秩 = 2。

几何意义：

两个向量 [ 1 , 0 ] [1, 0] [1,0] 和 [ 0 , 1 ] [0, 1] [0,1] 是正交的，可以撑开一个二维平面。
第三列 [ 2 , 3 ] [2, 3] [2,3] 被前两列组合出来（ 2 × [ 1 , 0 ] + 3 × [ 0 , 1 ] = [ 2 , 3 ] 2×[1,0] + 3×[0,1] = [2,3] 2×[1,0]+3×[0,1]=[2,3]），属于冗余信息。

总结方法：

核心思想：
- 秩 = 矩阵中线性无关的行（或列）的最大数量。
- 用初等行变换将矩阵简化为阶梯形，数非零行数即可。
技巧：
- 看是否有某行/列是其他行/列的倍数或组合。
- 零行或零列对秩无贡献（像行李箱里的空袋子）。
常见陷阱：
- 误以为矩阵的秩等于行数或列数（需看独立信息）。
- 行变换时计算错误（建议分步写中间结果）。

代码计算

python 复制代码

import numpy as np

E = np.eye(5)
print(E)
print("单位矩阵E的秩: \n",  np.linalg.matrix_rank(E))
A = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]])  # 根据列算 + 1
print("A的秩: \n", np.linalg.matrix_rank(A))

"""output:
[[1. 0. 0. 0. 0.]
 [0. 1. 0. 0. 0.]
 [0. 0. 1. 0. 0.]
 [0. 0. 0. 1. 0.]
 [0. 0. 0. 0. 1.]]
单位矩阵E的秩: 
 5
A的秩: 
 2
 """