Polar （极化）码的译码Ⅱ--BP 译码算法

[1 BP译码算法](#1 BP译码算法)

[1.1 因子图](#1.1 因子图)

[1.2 迭代传播公式](#1.2 迭代传播公式)

[2 BPL 译码算法](#2 BPL 译码算法)

[2.1 因子图](#2.1 因子图)

[2.2 迭代原理](#2.2 迭代原理)

[3 各种译码算法的性能对比](#3 各种译码算法的性能对比)

1 BP译码算法

1.1 因子图

基于 SC 的译码，由于是串行结构 ，在译码时延方面相较于并行译码结构劣势较大。然而，Polar 码其也可以采用并行译码结构，即 BP 译码，相应地其编码过程也可用 Forney 因子图来表示，如图所示，其中因子图可分为 n = 3 层，共包含 32 个节点。
N = 8 时 Forney 因子图
一般地，对于 ( N,K ) Polar 码，其相应的 Forney 因子图包含 n = log 2 N 层以及 (n + 1) N 个节点。每个节点由整数对 ( i, j ) 表示，其中 1 ≤ i ≤ n + 1 表示层索引，1 ≤ j ≤ N 表示行索引。第 i = n + 1 层的节点对应信道接收值，而第 i = 1 层的节点对应信源信息。每一层都包含 N/ 2 个处理单元，如图所示，其中。
BP 译码中的处理单元

1.2 迭代传播公式

在每个处理单元中其信息可进行双向传递，具体为在 t次迭代时，信息从右向左传递由表示，以及信息从左向右传递由表示。在 t = 0 时 ( 初始化 ) ，对于任意1 ≤ j ≤ N ，

其余节点均初始化为 0 ( 2 ≤ i ≤ n ) 。每一个处理单元 ( 1 ≤ i ≤ n ) 其从右向左传播的计算公式为：
从右向左传播的计算公式
从左向右传播的计算公式为：
从左向右传播的计算公式

初始化完成后，BP 译码器首先从右至左根据公式：
从右向左传播的计算公式

更新每个左节点 Li,j的信息，再从左至右根据公式：
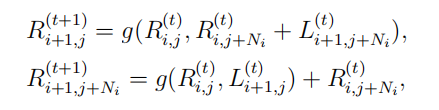从左向右传播的计算公式

更新每个右节点 Ri,j的信息，我们称所有左节点和右节点均更新一次为 BP 译码器的一次迭代，此时对应 t= 1。

在每次迭代完成 后，译码器会根据第 i= 1 层的所有节点信息估计信源序列，并根据第 i= n层的所有节点信息估计码字序列。在输出前，译码器将对估计的信源序列重新编码，并将其与码字序列进行校验(称为基于生成矩阵 G校验)：

若校验通过，则停止迭代；
否则将进行下一次迭代直到校验通过或达到设置的最大迭代次数 T。

2 BPL 译码算法

2.1 因子图

针对N= 8 时的 Forney 因子图，在 2009 年， R. Urbanke等人发现对于码长为 N 的二元 Polar 码，其 Forney 因子图共有 (log 2 N )! 种表示形式，我们称这些表示集合为**"** 过完备集" ，即其中 log 2 N 层的任意置换都是有效的表示，如图所示：
N = 8 时等效因子图
图中给出了 N = 8 时的三种等效因子图表示。同 LDPC 码的冗余停止从另一方面来看，对 Polar 码利用不同形式的 Forney 因子图进行 BP 译码可有效提升其译码性能。
BP 列表译码 (BPL) 算法 由 A. Elkelesh 等人在 2008 年时提出，与基于逐次抵消的列表译码 SCL 算法不同，其列表内并非是多个候选译码路径，而是多种译码 Forney 因子图：

即对于 SCL 算法，其列表大小是动态变化直到达到最多可保留的 L条路径，
而 BPL 算法是初始时就有独立的 L个译码器。

任何一个基于 Arıkan核置换的因子图都对应一个置换向量 Π ，该向量内的元素为从 1 到 n 的任何随机排列 (n = log2 N)。如图 " N = 8 时等效因子图 **"**所示，其 Π 分别对应 (3 , 2 , 1) ， (2 , 1 , 3) ，和 (2 , 3 , 1)。对于给定的输入，由于缺乏明确的关于最优译码置换因子图的理论指导，因此，为简单起见， BPL 算法中的 L 个译码器对应的因子图中，总是包含 n 个简单循环移位产生的因子图和 L − n个随机产生的置换向量生成的因子图，其具体流程图如图所示。
BPL 译码流程图

2.2 迭代原理

同 BP 译码一样， BPL 译码中的每个译码器的停止准则也是当其满足生成矩阵 G校验或直到满足最大迭代次数时停止迭代。在迭代停止后，我们也会得到 L个候选码字列表，但值得注意的是，仅那些满足生成矩阵 G 校验的码字为 Polar 码的有效码字。
BPL 译码器将选择距离信道输出 y 最近的，即欧氏距离最短的 ，有效码字作为译码输出。若 L 个译码器均无法得到有效码字，则认为译码失败，但 BPL 译码器仍以最近距离码字作为译码输出，即：

假设最大迭代次数为 T ， BPL 的译码复杂度为 O ( LT N log 2 N ) 。相比较 SCL 串行译码算法，尽管 BPL 算法减少了 SCL 算法中的排序复杂度，但当列表大小均为 L时，其复杂度仍远大于 SCL 译码算法。但在另一方面，BPL 译码算法基于迭代译码，其可得到译码软信息 (soft out-put)，这将有利于与调制相结合时的联合检测与译码。

3 各种译码算法的性能对比

下图给出了 N = 1024 ， R = 1 / 2 时， Polar 码经 AWGN 信道在 SC, SCL, BP, BPL 译码算法下的性能对比，其中 L = 4 和 L = 32 均考虑在 SCL 和 BPL 译码算法中。在 BP 和 BPL 译码算法中，最大迭代次数为 50 。
译码性能对比
上述所有 Polar 码均在构造信噪比为 SNR d = − 1 . 59 dB 下采用高斯近似 GA 构造。从上图中可以看出， BP 译码算法在低信噪比下优于 SC 译码算法，但基于 BP 并行结构的算法，无论是 BP 还是 BPL 译码算法，其在高信噪比下都会出现错误平层 (error floor) 。图中还可看出， BPL 译码算法的 FER 性能随 L 的增大而改善，但 SCL 译码 算法在高信噪比下，其列表大小 L = 4 和 L = 32 时的 FER 性能相似，且远优于 BPL 译码算法。