暑期算法训练.2

[6.力扣 11.盛水最多的容器](#6.力扣 11.盛水最多的容器)

[6.1 题目解析：](#6.1 题目解析：)

[6.2 算法思路：](#6.2 算法思路：)

[6.2.1 暴力解法：](#6.2.1 暴力解法：)

[6.2.2 优化算法：](#6.2.2 优化算法：)

[6.3 代码演示：](#6.3 代码演示：)

编辑

[6.4 总结反思：](#6.4 总结反思：)

[7.力扣 611.有效的三角形个数](#7.力扣 611.有效的三角形个数)

[7.1 题目解析：](#7.1 题目解析：)

[7.2 算法思路：](#7.2 算法思路：)

[7.3 代码演示：](#7.3 代码演示：)

编辑

[7.4 总结反思：](#7.4 总结反思：)

[8.力扣 LCR.179 查找总价格为目标值的两个商品](#8.力扣 LCR.179 查找总价格为目标值的两个商品)

[8.1 题目解析：](#8.1 题目解析：)

[8.2 算法思路：](#8.2 算法思路：)

[8.2.1 暴力解法：](#8.2.1 暴力解法：)

[8.2.2 优化解法：](#8.2.2 优化解法：)

[编辑8.3 代码演示：](#编辑8.3 代码演示：)

编辑

[8.4 总结反思：](#8.4 总结反思：)

[9.力扣 15.三数之和](#9.力扣 15.三数之和)

9.1题目解析：

[9.2 算法思路：](#9.2 算法思路：)

[9.3 代码演示：](#9.3 代码演示：)

[9.3.1 正确代码演示：](#9.3.1 正确代码演示：)

[9.3.2 错误代码演示：](#9.3.2 错误代码演示：)

[9.4 总结反思：](#9.4 总结反思：)

[10.力扣 18.四数之和](#10.力扣 18.四数之和)

[10.1 题目解析：](#10.1 题目解析：)

[10.2 算法思路：](#10.2 算法思路：)

[10.3 代码演示：](#10.3 代码演示：)

[10.4 反思总结：](#10.4 反思总结：)

6.力扣 11.盛水最多的容器

6.1 题目解析：

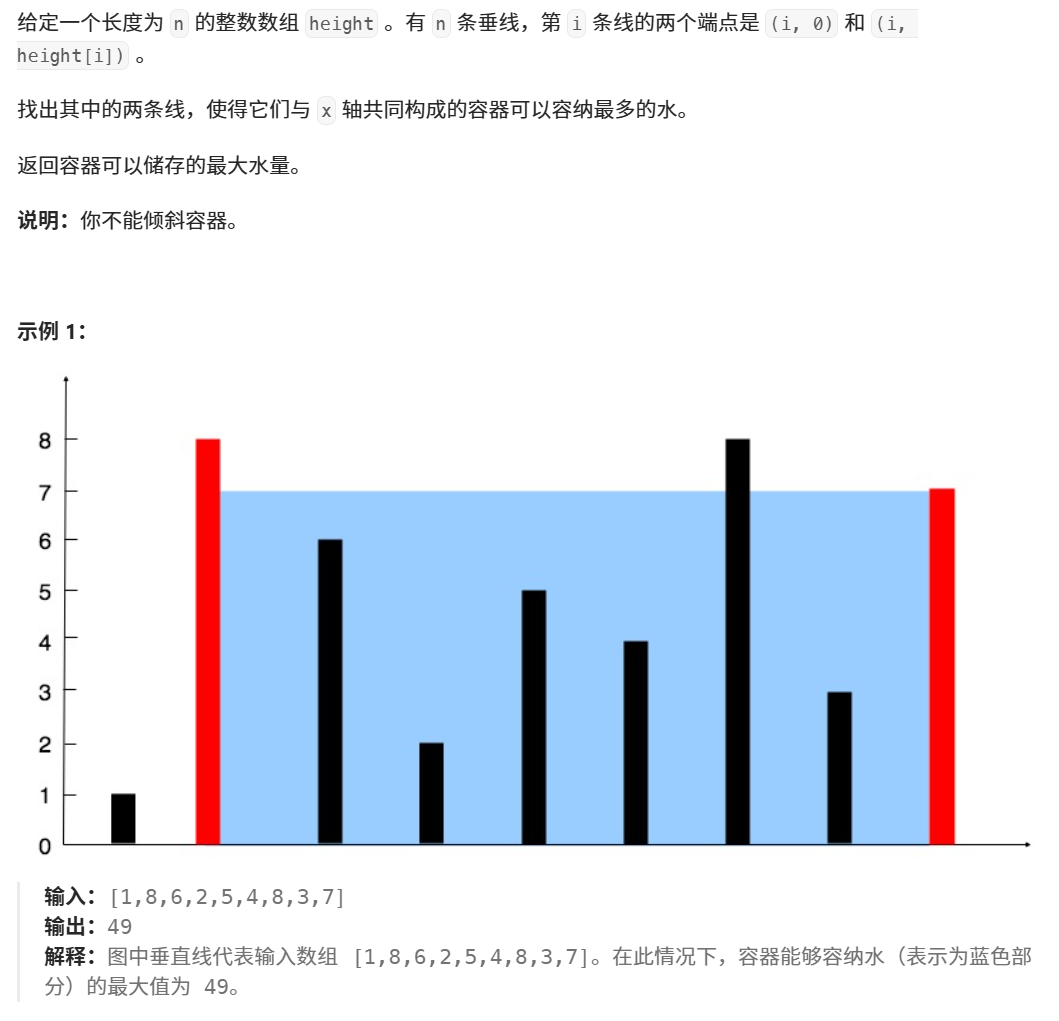
其实这道题目呢，就是让你在给定的数组内寻找到两个数相乘的最大值（但这i两个数字不是随便的两个数，由题意可得，这个"高"其实是遵循的是短板效应，即看的是短的那一边。）

6.2 算法思路：

6.2.1 暴力解法：

其实，当咱们看到一道题目的时候，最先想到的应该就是暴力解法，这道题也有对应的暴力解法。就是一个一个的进行枚举，相乘，然后选出最大的值即可。当然，容器的容积的计算：

1.首先得从height[i],height[j]中选出最小的值。

2.之后计算j-i的值，之后相乘即可。

那么咱们来看一下暴力解法的伪代码：

cpp 复制代码

for(int i=0;i<n;i++)
    for(int j=i+1;j<n;j++)
        check(nums[i],nums[i])

但是这样写的话，一旦给的数组里面的元素特别多，就会超时，所以第一种方法不可取。

6.2.2 优化算法：

这种算法是根据暴力解法的枚举改进而来。暴力解法为什么会超时？是因为它进行了太多的无意义的比较。

就拿这个进行举例子，暴力是不管三七二十一，直接全部进行相乘，然后比较。咱们其实可以带一带脑子，比如上图，你让j往左挪动，这个j-i是一直在减小的。而且，j往左挪动，由于挪动的边始终比i小，所以高也是在不段减小的。所以这个时候，就不需要再进行比较了，因为从i到j之间，不可能有比（j-i）*j更大的。那么此时就不需要比较这一部分。

还有一点就是，咱们要移动就移动短边，为什么呢？因为你越往内，这个长度越小，那么想找到比原来面积大的，只能靠高（找到比原来更高的高）。而咱们知道，这个受限于短板，所以高的大小得看短板，并且动短边，高度变大的可能性更大。想一想，因为它是取决于短边的。

所以，动的时候，先去比较左右板谁小，谁小谁就动，动完后再进行面积的计算，再比较这个面积与原面积，留下面积比较大的那一个。

6.3 代码演示：

cpp 复制代码

int main()
{
    vector<int> height = { 1,8,6,2,5,4,8,3,7 };
    int ret = 0;
    int left = 0;
    int right = height.size() - 1;
    while (left < right)
    {
        int tmp = min(height[left], height[right]) * (right - left);
        ret = max(ret, tmp);//找出最大的之间也要进行比较，选出更大的
        if (height[right] > height[left])
        {
            left++;
        }
        else
        {
            right--;
        }
    }
    cout << ret << endl;
    return 0;
}

代码就是左右板，谁小就动谁。

6.4 总结反思：

对于很多的题来说，优化的算法都是在暴力的基础上进行改良的。所以咱们一开始想不到优化的解法，不用慌张，先写出来暴力解法，然后再仔细的分析。

7.力扣 611.有效的三角形个数

7.1 题目解析：

这道题的题意很好理解，就是给你一个数组，返回数组里面可以组成三角形的三元组的个数即可。

7.2 算法思路：

相信大家都知道判断三角形的条件是任意两边之和大于第三边。但是呢，这个其实需要三个条件。但是呢，还有一种方法，只需要一个条件便可以判断出是否为三角形。

前提是咱们得知道这三条边的大小。

好，那么接下来讲解一下这道题运用到的算法思路：

找单调，然后用双指针解决这道问题：

1.首先得先排好序，因为要用那个结论，就得保证是升序的。

2.那么利用有序数组就是使用单调性。怎么个单调法呢？

3.首先固定住一个最大的数字。

4.在最大的数字的左边的区间内，使用双指针法计算出符合要求的三元组的个数。

很明显，得有两层循环才能完成吧。

假设此时a+b>c,那么从a往右一直到b这个区间内，都是比a大的，那么这个区间内的再加上b是不是也是一定大于c的？好，那么这个时候，你要是挪动a就没有任何意义了。这个时候，只需要往左挪动b即可。

此时的a+b<c,好，那么此时，从b往左一直到a的位置，这个区间内的值都是小于b的，所以a加上这个区间内的任意一个值，肯定也都是小于c的。所以此时挪动b无意义，需要将a往左挪动。

............以此类型。直到left>=right为止。

这才是完成了一个小循环，之后在移动c，再进行下一个小循环。

所以

那么到现在为止，代码相信大家都可以自己写出来了吧。

7.3 代码演示：

cpp 复制代码

int main()
{
    vector<int> nums = { 2,2,3,4 };
    //1.先进行排序
    sort(nums.begin(), nums.end());
    //2.进行计算个数
    int ret = 0;
    int n = nums.size();
    for (int i = n - 1; i >= 2; i--)
    {
        int left = 0;
        int right = i - 1;
        while (left < right)
        {
            if (nums[left] + nums[right] > nums[i])
            {
                ret += right - left;
                right--;
            }
            else
            {
                left++;
            }
        }
    }
    cout << ret << endl;
    return 0;
}

这是一个三元数组，所以c得到下标为2的位置停下。以及left与right必须得写在for里面，因为left，right随着c的变化为发生位置变化。

7.4 总结反思：

其实这道题也就是带我们认识到了单调性+双指针对于这类型题目的解法，为下面三道题打下了基础。

8.力扣 LCR.179 查找总价格为目标值的两个商品

8.1 题目解析：

题目很简单，就是给定一个数组，再给定一个值，让你在数组中寻找两个元素和为目标值的二元数组，并且不管元素顺序，返回一种叫即可。

8.2 算法思路：

8.2.1 暴力解法：

这道题搭眼一看，就知道肯定有暴力解法，就是写两层for循环，然后再将元素想加，看看哪两个元素相加等于目标值，再返回这两个元素组成的二元数组。但是这种解法容易超时，所以咱们重点来讲解第二种优化算法。

8.2.2 优化解法：

其实这个题的解法与上一题的解法基本一致，咱们来看图理解：

8.3 代码演示：

cpp 复制代码

vector<int> Judgment(vector<int>& price, int target)
{
    int left = 0;
    int right = price.size() - 1;
    while (left < right)
    {
        if (price[left] + price[right] > target)
        {
            right--;
        }
        else if (price[left] + price[right] < target)
        {
            left++;
        }
        else return { price[left],price[right] };//多参数隐式类型转换
    }
    return{ -1,-1 };//确保每个路径下都有返回值
}

8.4 总结反思：

这道题与上一道题的解法基本一致。

9.力扣 15.三数之和

9.1题目解析：

题目也挺好理解的，就是i，j，k三个元素相加为0，并且这三个元素不可以是同一个位置的，并且返回的时候，三元数组中的元素相同的，只能返回一组，这个意味着咱们是不是要进行去重呀。那去重的话，咱们肯定可以想到C++里面的unordered_set，使用容器去重。当然可以，但是，有没有不使用容器就可以进行去重的呢？有！方法，咱们算法思路里面讲解。

9.2 算法思路：

其实，这道题，你只要做过前面的那个题，这个题的算法思路就很容易想到。

好，这个题基本的核心的思路我已经全部罗列出来了，大家可以看一下。但这个地方，本博主写代码的时候，还是被弄晕了。

9.3 代码演示：

9.3.1 正确代码演示：

cpp 复制代码

vector<vector<int>> threeSum(vector<int>& nums)
{
    sort(nums.begin(), nums.end());
    vector<vector<int>> ret;
    int n = nums.size();
    int i = 0;
    while (i < n)
    {
        int left = i + 1; int right = n - 1;
        while (left < right)
        {
            if (nums[left] + nums[right] == -nums[i])
            {
                vector<int> frontret = { nums[left],nums[right],nums[i] };
                ret.push_back(frontret);
                left++, right--;
                // 去重操作left和right，先++left,--right,再去重
                //先去重，再移动left与right的方法不可取
                while (left < right && nums[left] == nums[left - 1]) left++;
                while (left < right && nums[right] == nums[right + 1])right--;
            }
            else if (nums[left] + nums[right] > -nums[i])
            {
                right--;
            }
            else {
                left++;
            }
        }
        i++;//外层i去重
        while (i < n && nums[i] == nums[i - 1]) i++;
    }
    return ret;
}
int main()
{
    vector<int> nums = { 2,-3,0,-2,-5,-5,-4,1,2,-2,2,0,2,-4,5,5,-10 };
    vector<vector<int>> kk = threeSum(nums);
    for (auto& e : kk)
    {

        for (auto& m : e)
        {
            cout << m << "";
        }
        cout << endl;
    }
    cout << endl;
}

这个地方的去重操作呢，必须得是先进行left，right的移动，之后再判断这个位置与前一个位置的数字是否相等，如果相等，再加加，挪到要改变的那个元素的位置上。这是正确的逻辑。但是博主呢，正好逻辑相反，结果就这一个题在那里调试了一下午。

9.3.2 错误代码演示：

cpp 复制代码

去重逻辑混乱，不可取
vector<vector<int>> threeSum(vector<int>& nums)
{
    sort(nums.begin(), nums.end());
    vector<vector<int>> ret;
    int n = nums.size();
    int i = 0;
    while (i < n)
    {
        int cout_i = 0;
        int left = i + 1; int right = n - 1;
        while (left < right)
        {
            int cout_left = 0;
            int cout_right = 0;
            if (nums[left] + nums[right] == -nums[i])
            {
                vector<int> frontret = { nums[left],nums[right],nums[i] };
                ret.push_back(frontret);
                while ((left + 1 < n - 1) && (nums[left] == nums[left + 1]))
                {
                    if (left < n - 1)
                    {
                        left += 1;
                        cout_left++;
                    }
                }
                while ((right - 1 > i + 1) && (nums[right] == nums[right - 1]))
                {
                    if (right > i + 1)
                    {
                        right -= 1;
                        cout_right++;
                    }
                }

                if ((left < n - 2) && (cout_left == 0))
                {
                    left++;
                }
                if ((right > i + 2) && (cout_right == 0))
                {
                    right--;
                }
            }
            else if (nums[left] + nums[right] > -nums[i])
            {
                right--;
            }
            else {
                left++;
            }
        }
        while ((i + 1 < n - 2) && (nums[i] == nums[i + 1])  )
        {
            if (i < n - 2)
            {
                i += 2;
                cout_i++;
            }
        }

        if (cout_i == 0)
        {
            i++;
        }
    }
    return ret;
}
int main()
{
    vector<int> nums = { 2,-3,0,-2,-5,-5,-4,1,2,-2,2,0,2,-4,5,5,-10 };
    vector<vector<int>> kk = threeSum(nums);
    for (auto& e : kk)
    {

        for (auto& m : e)
        {
            cout << m << "";
        }
        cout << endl;
    }
    cout << endl;
}

这是我写的代码，我的本意是想着既然都去重了，那就先去重，如果重复了，那就加到不重复为止，且这种最后不需要再单独加加了。之后再单独加。但是呢，不对。

**去重指针移动不正确**：在找到一组解后，对`left`和`right`的去重没有正确地将指针移动到下一个不同元素的位置。例如，如果`left`位置有重复，它只是移动到了重复序列的最后一个，然后停止，这样下一次循环还是相同的值（因为下一次循环时，`left`指向的还是重复序列的最后一个，而下一个元素就是不同的，但此时`left`并没有指向下一个不同元素，所以循环会继续使用这个重复序列的最后一个元素，导致重复解）。

**去重后指针移动逻辑混乱**：通过`cout_left`和`cout_right`来决定是否再移动一次，这种逻辑没有道理。而且，在去重循环中，它只移动了重复元素，但并没有确保移动后的指针指向的是一个新的值（即跳过重复后应该指向下一个不同的值）。

**固定数`i`的去重逻辑错误**：使用`i+=2`来跳过重复，这会导致当重复次数为奇数时，最后一个重复值仍然会被处理，造成重复解。而且，当重复次数超过2次时，跳跃步长固定为2，显然不够。

只能说，我还是个新手吧哈哈哈哈，做题做的还是少。

9.4 总结反思：

这道题想要真正的自己用代码实现出来，真的挺不容易的。还是要多练习题目。

10.力扣 18.四数之和

10.1 题目解析：

你仔细的读一读这道题，会发现，这道题的解法与前面那个三数之和的解法基本一致。无非就是外面多套了层循环，多加了一个去重。

10.2 算法思路：

若还是不能够理解，那么我画一张图就可以了：

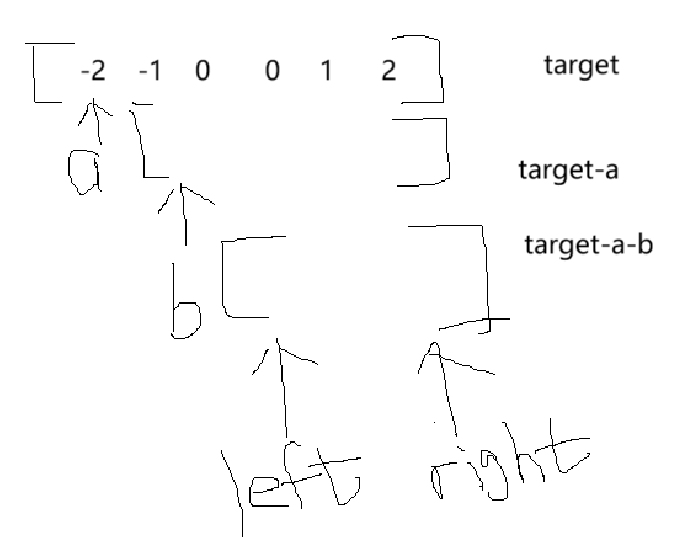1.依次固定一个数a

2.在a后面的区间内，利用"三数之和"找到三个数，使这三个数的和等于target-a即可

2.1 依次固定一个数b

2.2 在b后面的区间内，利用"双指针"找到两个数，使得两个数的和为target-a-b即可

最后别忘了去重细节，有三个，left与right，b，a

以及还有越界的情况。最后考虑清楚，会发现与三数之和的代码差不多一样的。

10.3 代码演示：

cpp 复制代码

//四数之和思想与三数之和基本一致，连去重方法都是一样的
vector<vector<int>> fourSum(vector<int>& nums, int target) {
    vector<vector<int>> ret;
    sort(nums.begin(), nums.end());
    int n = nums.size();
    for (int i = 0; i < n;) {

        for (int j = i + 1; j < n;) {
            int left = j + 1;
            int right = n - 1;
            long long aim = (long long)target - nums[i] - nums[j];
            while (left < right) {
                if (nums[left] + nums[right] ==
                    aim) {
                    vector<int> frontret = { nums[left], nums[right],
                                            nums[i], nums[j] };
                    ret.push_back(frontret);
                    ++left;
                    --right;
                    // 只有这样写才能确保最后一个位置的元素是在不重复的那个位置底下
                    while (left < right && nums[left] == nums[left - 1]) {
                        left++;
                    }
                    while (left < right && nums[right] == nums[right + 1]) {
                        right--;
                    }
                }
                else if (nums[left] + nums[right] >
                    aim) {
                    right--;
                }
                else {
                    left++;
                }
            }
            j++;
            while (j < n && nums[j] == nums[j - 1]) {
                j++;
            }
        }
        i++;
        while (i < n && nums[i] == nums[i - 1]) {
            i++;
        }
    }
    return ret;
}

三个去重以及边界判定别忘了。

10.4 反思总结：

题目之间都是相互连接的，咱们只有真正弄懂了一道题目，理解其中的解法，再遇到下一个题目的时候，才有应对之策，才能临阵不慌。

...............本篇完

暑期算法训练.2

6.力扣 11.盛水最多的容器

6.1 题目解析：

6.2 算法思路：

6.2.1 暴力解法：

6.2.2 优化算法：

6.3 代码演示：

6.4 总结反思：

7.力扣 611.有效的三角形个数

7.1 题目解析：

7.2 算法思路：

7.3 代码演示：

7.4 总结反思：

8.力扣 LCR.179 查找总价格为目标值的两个商品

8.1 题目解析：

8.2 算法思路：

8.2.1 暴力解法：

8.2.2 优化解法：

8.3 代码演示：

8.4 总结反思：

9.力扣 15.三数之和

9.1题目解析：

9.2 算法思路：

9.3 代码演示 ：

9.3.1 正确代码演示：

9.3.2 错误代码演示：

9.4 总结反思：

10.力扣 18.四数之和

10.1 题目解析：

10.2 算法思路：

10.3 代码演示：

10.4 反思总结：

9.3 代码演示：