力扣.1312让字符串成为回文串的最少插入次数力扣.105从前序和中序遍历构造二叉树牛客.拼三角力扣.57插入区间编辑

力扣.1312让字符串成为回文串的最少插入次数

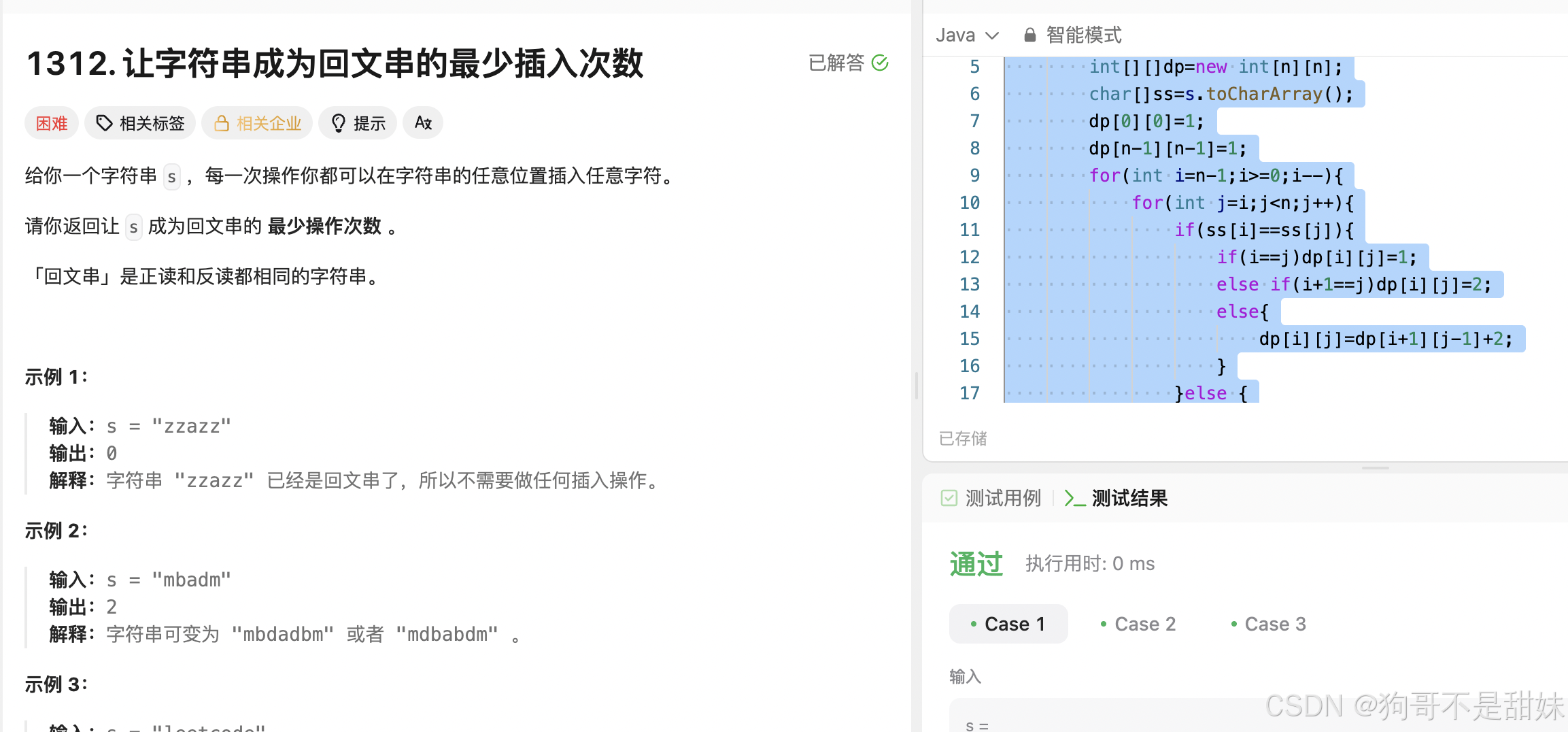
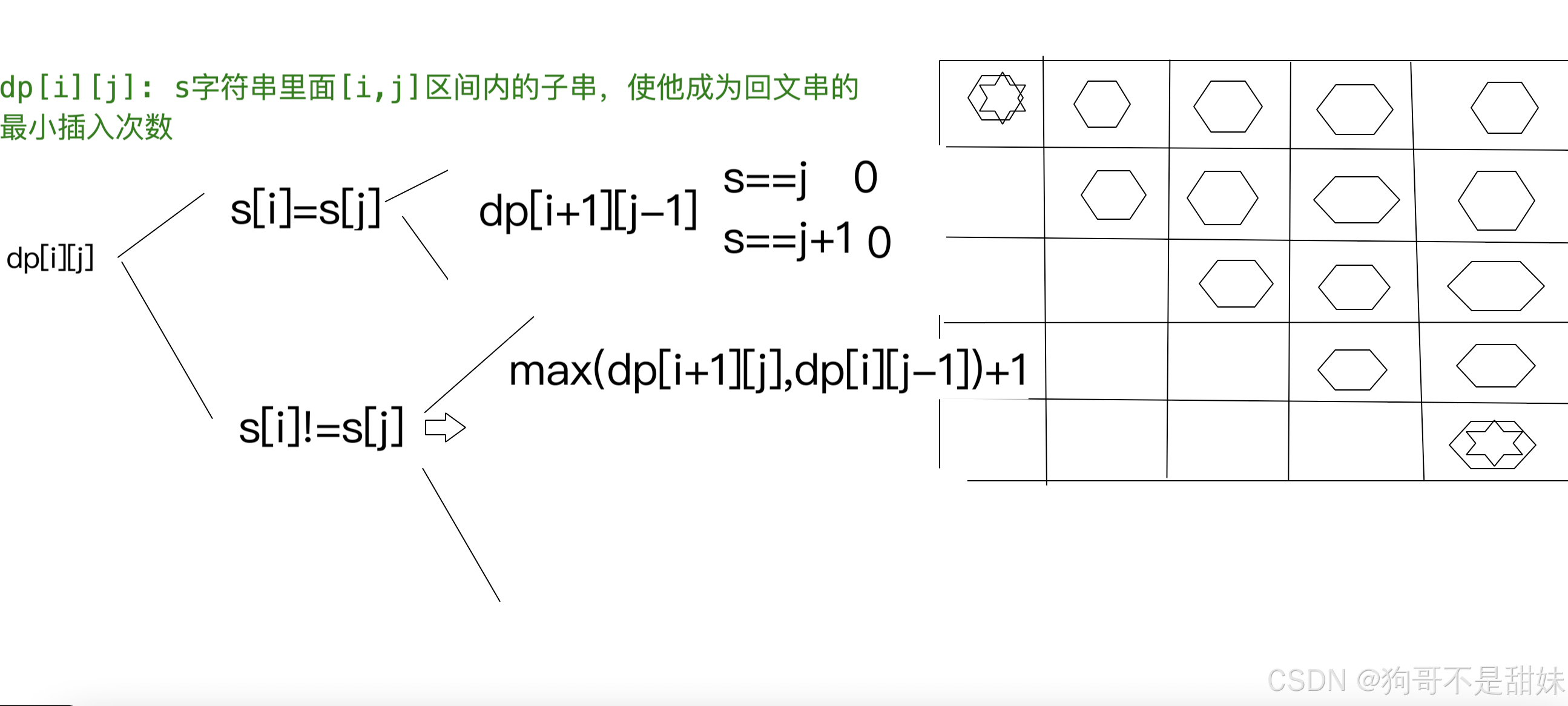
这个题，我说实话，真没想到思路，我尝试像是以前那种给他写一遍回文

比如mbadm mdabm 就是倒着写，然后还是没有思路，然后我又观察，为啥是回文串呢？

他这个比如最下面这个

解法1:leetcode他这个是以o作中心，或者以d做中心都可以，都是复制相同的个数，那么你再一想，一个是eoe和ede 这是变成回文的核心，是不是都是3个满足回文，其余的不满足

也就是总数-满足回文的最大个数

复制代码

class Solution {
    public int minInsertions(String s) {
        int n=s.length();
        //寻找最长的回文子序列，然后总长度去剪去就好
        int[][]dp=new int[n][n];
        char[]ss=s.toCharArray();
        dp[0][0]=1;
        dp[n-1][n-1]=1;
        for(int i=n-1;i>=0;i--){
            for(int j=i;j<n;j++){
                if(ss[i]==ss[j]){
                    if(i==j)dp[i][j]=1;
                    else if(i+1==j)dp[i][j]=2;
                    else{
                        dp[i][j]=dp[i+1][j-1]+2;
                    }
                }else {
                    dp[i][j]=Math.max(dp[i+1][j],dp[i][j-1]);
                }
            }
        }

      return n-dp[0][n-1];
    }
}

解法2:

//dp[i][j]=s里面[i,j]区间内的子串，使他成为回文串的最小插入次数

初始化i与j关系，j>=i

为啥是+1，也很有意思，我的理解是，i ...... j 当 s[i]!=s[j]的时候，给i的左边添加一个s[j]这样s[j]=s[j] 那么我只需要保证i-j-1位置是回文就好，所以dp[i][j-1]那么下面同理

i==j为0，不用初始化，那么i最有可能越界的就是i+1=j这条线，但是你思考一下

i+1=j这条线就没有一个是越界的，所以不用初始化
复制代码
class Solution {
    public int minInsertions(String s) {
        int n=s.length();
        //解法2
        //dp[i][j]: s字符串里面[i,j]区间内的子串，使他成为回文串的最小插入次数  
        int[][]dp=new int[n][n];
        char[]ss=s.toCharArray();
        
        for(int i=n-1;i>=0;i--){
            for(int j=i;j<n;j++){
                if(i==j){
                    dp[i][j]=0;
                }
                else if(ss[i]==ss[j]){
                        dp[i][j]=dp[i+1][j-1];
                }
                else{
         //           abc
                    dp[i][j]=Math.min(dp[i+1][j],dp[i][j-1])+1;
                     }
                }
            }

      return dp[0][n-1];
    }
}

力扣.105从前序和中序遍历构造二叉树

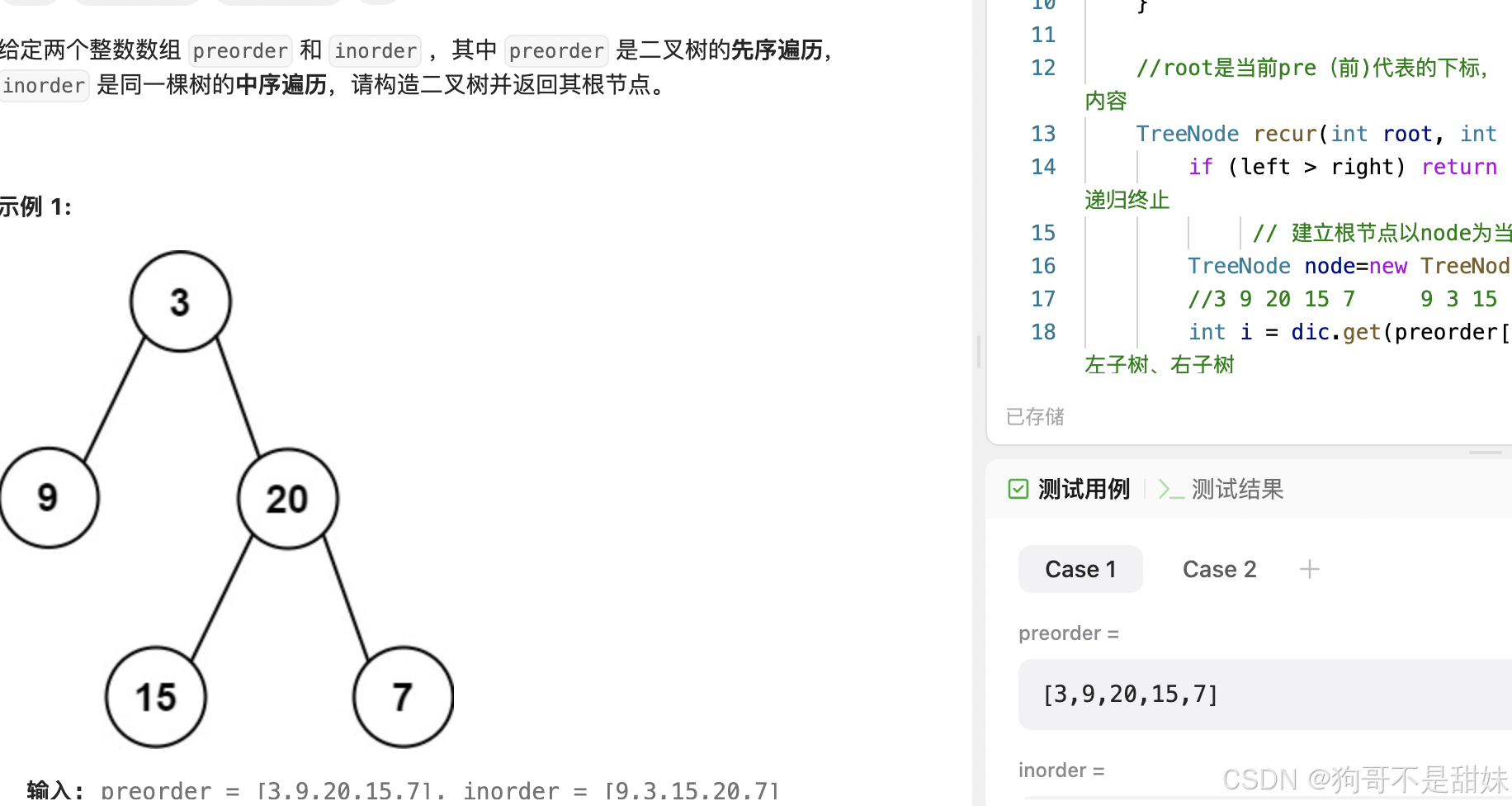
// left i-1, root(i） , i+1 right 分为这个五个部分，(中序)

难点就是，怎么找到右子树的根在前序的节点

当前的根节点长度 root 去加上一个左子树的长度，因为先序是根左右，左子树长度通过中序计算，然后+1,因为你不加一，是左子树的右边界

所以需要root+i-1-left+1+1.

复制代码

class Solution {
    int[] preorder; //定义为全局，应该是不用穿参数啥的方便
    HashMap<Integer, Integer> dic = new HashMap<>();
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        this.preorder = preorder;
        for(int i = 0; i < inorder.length; i++)
            dic.put(inorder[i], i);
            //map里面放入存储的值，以及对应的下标
        return recur(0, 0, inorder.length - 1);
    }

    //root是当前pre（前)代表的下标， preorder[root]是要在中序遍历中寻找的内容
    TreeNode recur(int root, int left, int right) {
        if (left > right) return null;                          // 递归终止
             // 建立根节点以node为当前根节点
        TreeNode node=new TreeNode();     
        //3 9 20 15 7     9 3 15 20 7
        int i = dic.get(preorder[root]);             // 划分根节点、左子树、右子树
 //       left     i-1,     root      ,  i+1      right
                     // 开启左子树递归
        node.left=recur(root-1,left,i-1);            
         // 开启右子树递归
         根的索引+左子树的索引+1
         //i-1-left+1+root+1;
        node.right=recur(i-left+root+1,i+1,right);  
        return node;                                           // 回溯返回根节点
    }
}

牛客.拼三角

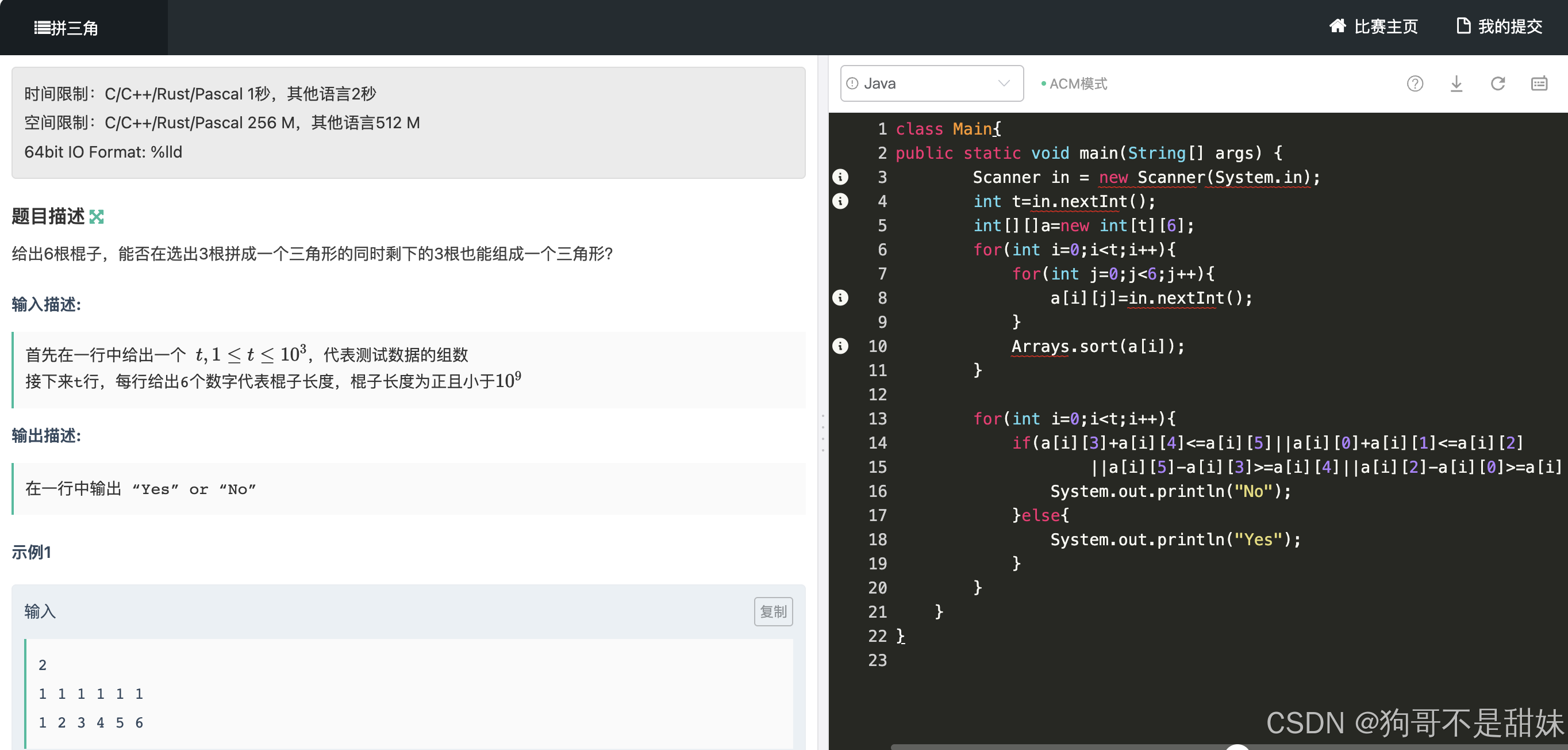
三重for循环:

a b c d e f C6^3=20 abc 枚举 def def枚举abc 20/2=10 折一半就好

三重for循环，枚举三个数的，三个数字不一样,( 就去检查一下) check()

2.dfs() 万能的，比如 100个里面找到50个，枚举第几个格子

3.基于前两种函数

如何快速判断abc,是否可以构成三角形，比如a,b,c (a,b,c排序之后) 两边之和大于最大边

0,1,2 3,4,5 (只判断一次就好,2成了，全成，不成全不成) 0,2,3 -1,4,5 0,3,4 1,2,5

0,1,3 1,4,5 0,2,4-1,3,5

0,1,4 2,3,5 0,2,5 -1,3,4

仅仅需要枚举0，1，2 3，4，5 0，2， 3， 1， 4， 5

0， 3， 4 1，2，5

复制代码

import java.util.*;
public class Main{
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int t=in.nextInt();
        int[][]a=new int[t][6];
        for(int i=0;i<t;i++){
            for(int j=0;j<6;j++){
                a[i][j]=in.nextInt();
            }
            Arrays.sort(a[i]);
        }

        for(int i=0;i<t;i++){
            if(a[i][3]+a[i][4]>a[i][5]&&a[i][0]+a[i][1]>a[i][2]||
               a[i][0]+a[i][2]>a[i][3]&&a[i][1]+a[i][4]>a[i][5]||
               a[i][0]+a[i][3]>a[i][4]&&a[i][1]+a[i][2]>a[i][5]||
               a[i][0]+a[i][4]>a[i][5]&&a[i][1]+a[i][2]>a[i][3]){
                System.out.println("Yes");
            }else{
                System.out.println("No");
            }
        }
    }
}

力扣.57插入区间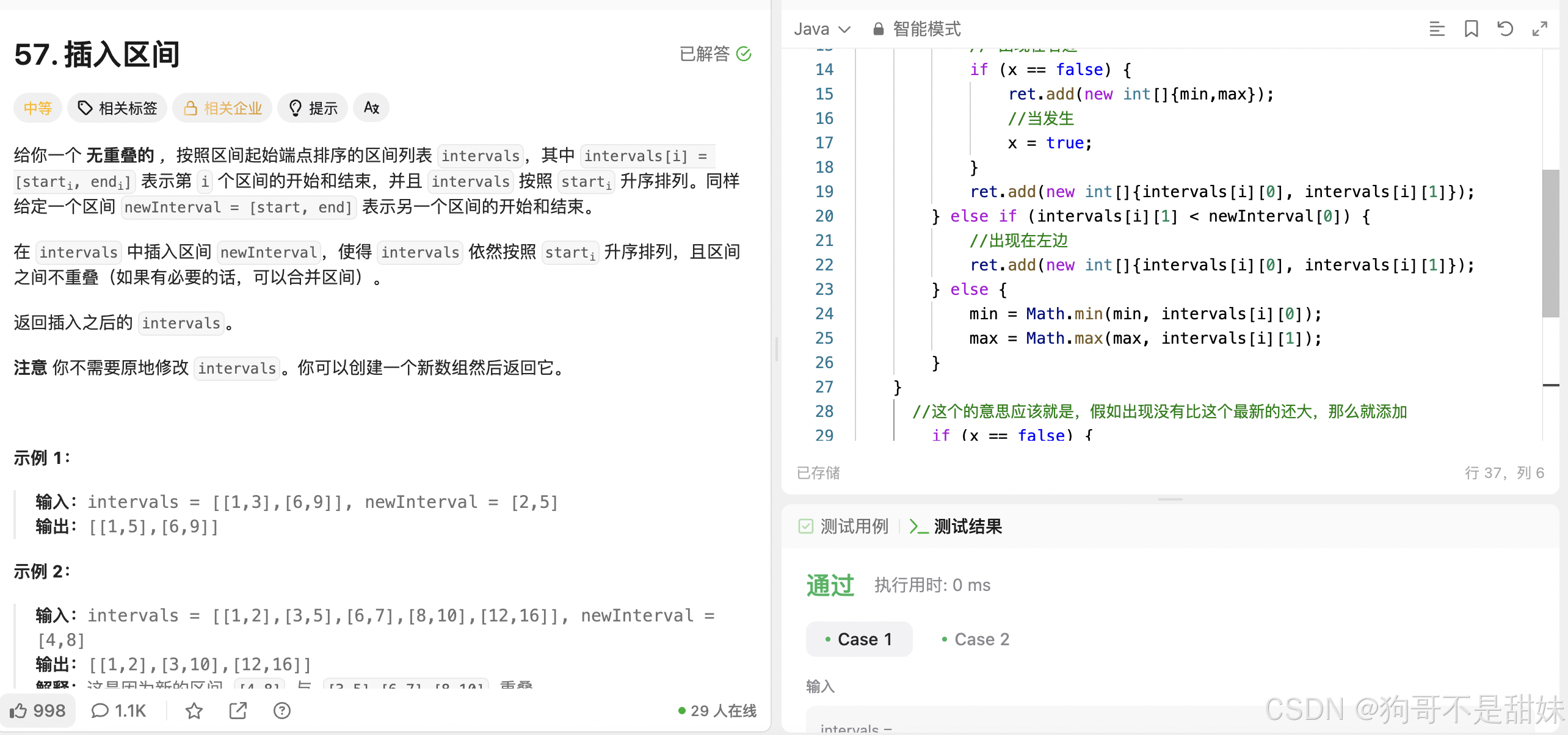

她这个不好想，难点是在主要我这个进行一个区间的判断，有的判断，你很容易产生其他误区，比如分的太细，又比如分的很粗，就会导致模拟的情况过于复杂。

他应该先把不符合条件的排除，比如我插入的区间，跟你一点关系都没有的我需要给他排出了，然后去找重叠的部分，重叠的部分，就是重叠这段区间里面的最小值和最大值，把这俩抽出来就好，但是我们什么时候，插入这个区间呢，是不是应该，当我们第一次当前区间超过插入的区间的时候，插入区间内的值(但是此时是否涉及一个，假如没有比插入的区间大的情况，所以后面我们给他做了一个特殊处理，给他最后判断了一下，假如部署true,就去插入一下。

复制代码

class Solution {
       public int[][] insert(int[][] intervals, int[] newInterval) {
    ArrayList<int[]>ret=new ArrayList<>();
    int n=intervals.length;
    int min=newInterval[0];
    int max=newInterval[1];
    boolean x=false;
    for(int i=0;i<n;i++) {
        //两种情况，第一种全部合并（可能覆盖多种情况)
        //第二张情况部分合并(比如4，8 3，8）
        //第三种直接插入
        if (intervals[i][0] > newInterval[1]) {
            // 出现在右边
            if (x == false) {
                ret.add(new int[]{min,max});
                //当发生
                x = true;
            }
            ret.add(new int[]{intervals[i][0], intervals[i][1]});
        } else if (intervals[i][1] < newInterval[0]) {
            //出现在左边
            ret.add(new int[]{intervals[i][0], intervals[i][1]});
        } else {
            min = Math.min(min, intervals[i][0]);
            max = Math.max(max, intervals[i][1]);
        }
    }
      //这个的意思应该就是，假如出现没有比这个最新的还大，那么就添加
        if (x == false) {
            ret.add(new int[]{min, max});
        }
        int[][] ans = new int[ret.size()][2];
        for (int i = 0; i < ret.size(); ++i) {
            ans[i] = ret.get(i);
        }
        return ans;
    }
}