圆方树学习笔记 —— 一种关于点双连通分量的思考方式

引言

本文原名为《圆方树学习笔记 & 最短路题解》，原始版本可见文末。

本文旨在系统梳理 圆方树（Block forest） 及其思想在图论问题中的应用，尤其是在信息学奥林匹克竞赛（OI）中的实际价值。

我们将从一种特殊的图结构------仙人掌图（Cactus Graph）出发，逐步扩展至一般无向图，分析如何通过构造圆方树，来将复杂图上问题转化为树上问题，并借助经典算法（如树形 DP、树链剖分、DDP、虚树等）解决。

本文对涉及的问题进行了系统归类，并配有例题与代码，构建出一套完整的知识体系，帮助读者深入理解核心思想并掌握其在实际题目中的变形与拓展。当然，并非所有问题都需要显式构造圆方树，部分情况下我们仅借助其结构思想进行分析和维护。

在此基础上，本文还创新性地提出了「圆树」这一辅助结构的概念，以优化特定类型问题的建模与求解过程。

希望本笔记能为正在学习相关内容的读者提供一套完整、实用的参考资料。

全文约二十万字符，除代码外有五万字，因此建议阅读的同时做题来巩固知识。

问题引入

在处理无向图上的复杂问题时，我们常借助图的结构性质进行化简，在简化后的图上使用算法解决问题。比如，使用 Tarjan 算法对图进行缩点：

• 强连通分量 缩点后可构成一个有向无环图（DAG）；
• 边双连通分量 缩点后可转化为一棵树；
• 那么，点双连通分量缩点之后，会变成什么结构？

答案是：圆方树（Block forest）。

圆方树正是对图进行点双连通分量 缩点后的结构表示。它将原图中复杂的连通关系映射为树上的结构，从而使许多原本难以处理的问题得以简化为树上问题，显著降低分析与求解的难度。

圆方树的定义

在一张无向图中，对每个点双连通分量建立一个对应的超级节点，并将该分量中所有原图中的点与该超级节点相连，随后删除原图中的所有边。在构建完成后：

• 将这些新增的超级节点称为 「方点」；
• 将原图中的普通节点称为 「圆点」；

这样得到的一棵圆点与方点交错连接的树结构，即为该图的圆方树。

在圆方树上，一个方点的父亲一定是圆点，我们称这个圆点为它的 「父亲圆点」 ，类似定义 「孩子圆点」 ，对于一个圆点类似定义 「父亲方点」 ，「孩子方点」。

以下展示的是一张无向图及其对应的圆方树结构。例如，原图中点双 \(\{2,3,4,5\}\) 对应超级节点 \(15\)，在圆方树中，\(15\) 和 \(2,3,4,5\) 都连有边。

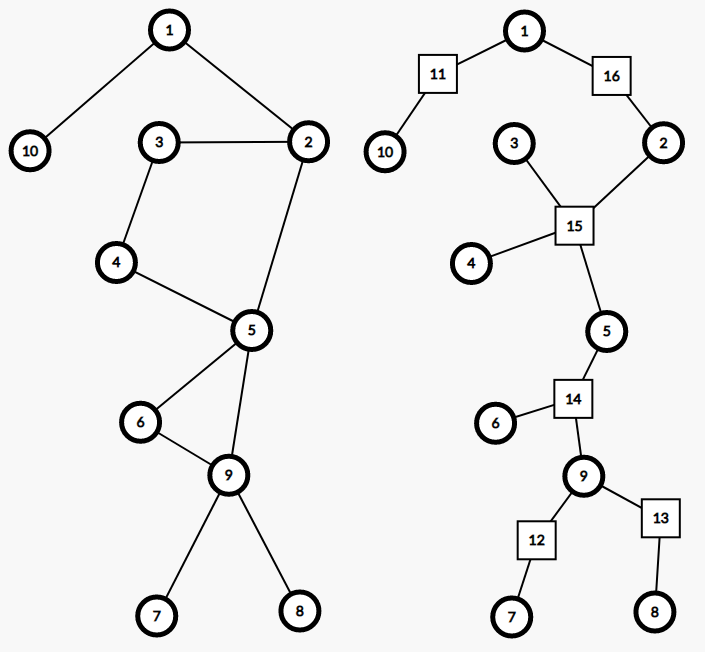
本文中，若无特殊说明，认为「两点被一条边连接」这种图结构 是一个点双 ，如上图中 \(\{8,9\}\)。并为这种点双同样创建一个方点。即在圆方树上不会出现两个圆点直接相连的情况，即不出现圆圆边。

圆方树的简单性质

我们首先需要对圆方树的基本特点有一定了解。

1. 圆方树节点数小于 \(2n\)，其中 \(n\) 为原图点数。

   一个点双引入一个方点，一张图的点双最多只有 \(n-1\) 个，这个上界在图退化为树的情况下达到。所以代码中不要忘记给相关数组开两倍大小。

2. 圆方树上一种类型的点只会和另一种类型的点连边。

   方点只会和圆点连边，圆点只会和方点连边。由定义不难得到这一点。

3. 圆方树上任意一条树链都是「圆方交错」的。

   结合上一条性质，不难发现这个性质。

圆方树构建方式

一种简洁而典型的圆方树建树方法是：在运行 Tarjan 算法求点双连通分量的同时构造圆方树 。并且可以直接把圆方树建成一棵外向树 ，便于后续树上遍历。我们直接让方点从 \(n+1\) 开始编号，圆点保持原图上的编号。

void tarjan(int u, int fr) {
    dfn[u] = low[u] = ++timer;
    stack[++top] = u;
    for (int i = G.head[u]; i; i = G.edge[i].nxt) {
        if (i == (fr ^ 1)) continue;
        int v = G.edge[i].v;
        if (!dfn[v]) {
            tarjan(v, i);
            low[u] = min(low[u], low[v]);
            if (low[v] >= dfn[u]) {
                ++dcc_cnt;
                while (true) {
                    int x = stack[top--];
                    T.add(dcc_cnt + n, x); // 连边：方点 -> 圆点
                    if (x == v) break;
                }
                T.add(u, dcc_cnt + n);     // 连边：圆点 -> 方点
            }
        } else {
            low[u] = min(low[u], dfn[v]);
        }
    }
}

这是最基础的构建框架，在后文具体问题中，我们将在此代码的基础上进行拓展，比如，为圆方树赋上边权，维护当前点双的子图。

圆方树维护点对间所有简单路径信息

关于原图中两点 \(u,v\) 之间所有的简单路径，我们可以将其映射到圆方树上 \(u,v\) 之间的树链，并且借助圆方树的树形结构，来维护这些所有简单路径的信息和。

点对间所有简单路径信息

对于圆方树的映射方式，等到我们分析完信息维护的方式，就呼之欲出了。

我们先来看几种典型的信息：\(u,v\) 间最长简单路径长度、\(u,v\) 间简单路径条数、\(u,v\) 间所有简单路径长度之和、所有能被某一条 \(u,v\) 间简单路径经过的点权和。

我们可以大致分为如下两类。

类型一：满足分配率的边权、点权相关信息

让我们尝试用形式化的语言来形容，进行适当抽象。

设 \(p_i(u,v)\) 表示某一条 \(u\rightarrow v\) 的简单路径。对于这一条简单路径的信息，如果可以看做其中每一条边 \(e\in p_i(u,v)\) 的信息 \(\operatorname{info}(e)\) 按照一种特定的合并方式 \(\odot\) 合并后的结果，我们就称这种信息为 「边权相关信息」 ，即路径 \(p_i(u,v)\) 的信息为 \(\operatorname{info}(p_i(u,v)) = \bigodot\limits_{e\in p_i(u,v)}\operatorname{info}(e)\)。类似定义点权相关信息，处理这种信息，可以把所有点的点权按照一种方式变成边权，除了某一点需要特殊考虑，剩下维护的就是边权相关信息。因此为了简化讨论，仅考虑边权相关信息。例如：「路径长」是边权相关信息，对于一条边 \(e\)，\(\operatorname{info}(e)\) 就是 \(e\) 的长度 \(\operatorname{len}(e)\)，\(\odot\) 即为 \(+\)，\(\operatorname{info}(p_i(u,v)) = \bigodot\limits_{e\in p_i(u,v)}\operatorname{info}(e) = \sum\limits_{e\in p_i(u,v)}\operatorname{len}(e)\)。

所求的是对于 \(u,v\) 间所有简单路径的信息，按照 \(\oplus\) 合并后的结果，即 \(\operatorname{info}(u,v)=\bigoplus_i\operatorname{info}(p_i(u,v))\)。\(\oplus\) 显然需要满足交换律，否则答案就不唯一了。例如，对于「最长简单路径长度」，就是「路径长」通过 \(\max\) 合并后的信息，\(\odot=+\)，\(\oplus=\max\)，\(\operatorname{info}(u,v)=\max_i\operatorname{info}(p_i(u,v))=\max_i\sum\limits_{e\in p_i(u,v)}\operatorname{len}(e)\)。

明确需要求解什么后，考虑如何维护。

考虑什么情况下可能可以合并 \(\operatorname{info}(u,v)\) 与 \(\operatorname{info}(v,w)\) 得到 \(\operatorname{info}(u,w)\)。发现当且仅当 \(v\) 是割点的时候，合并信息，才可能得到不重不漏的的结果。因为 \(v\) 作为割点，\(u\rightarrow w\) 的每一条简单路径总是可以拆分成 \(u\rightarrow v\) 和 \(v\rightarrow w\) 两条仅在 \(v\) 处相交的简单路径。这是类似于卷积的，即对于所有 \(i,j\)，\(p_i(u,v)\sim p_j(v,w)\) 拼出了一条 \(p_k(u,w)\)，并且这种 \(i,j\mapsto k\) 的映射是唯一的。那么 \(\operatorname{info}(u,w)=\bigoplus_k\operatorname{info}(p_k(u,w))=\bigoplus_{i,j}\operatorname{info}(p_i(u,v)\sim p_j(v,w))\)。

在树上，因为 \(u\rightarrow v\) 和 \(v\rightarrow w\) 的简单路径是唯一的，我们有 \(\operatorname{info}(u,w)=\operatorname{info}(u,v)\oplus\operatorname{info}(v,w)\)，这是简单的。但是此时 \(u\rightarrow v\) 和 \(v\rightarrow w\) 的简单路径不是唯一的，就不能直接通过 \(\oplus\) 合并了。

有时候我们能够找到一种运算 \(\otimes\)，使得我们可以打开这个 \(\bigoplus\)，直接合并两个子问题的信息。它需要满足 \(\bigoplus_{i,j}\operatorname{info}(p_i(u,v)\sim p_j(v,w))=\Big(\bigoplus_{i}\operatorname{info}(p_i(u,v))\Big)\otimes\Big(\bigoplus_{j}\operatorname{info}(p_j(v,w))\Big)\)，也就是通过 \(\otimes\) 类似树上直接合并两个子问题的信息。把 \(\operatorname{info}\) 用 \(\odot\) 表示，也就是 \(\bigoplus_{i,j}\bigodot_{e\in p_i(u,v)\sim p_j(v,w)}\operatorname{info}(e)=\Big(\bigoplus_{i}\bigodot_{e\in p_i(u,v)}\operatorname{info}(e)\Big)\otimes\Big(\bigoplus_{j}\bigodot_{e\in p_j(v,w)}\operatorname{info}(e)\Big)\)。为了方便观察，不妨用 \(S_i\) 表示 \(p_i(u,v)\)，\(T_i\) 表示 \(p_i(v,w)\)，等式变为：\(\bigoplus_{i,j}\bigodot_{e\in S_i\cup T_j}\operatorname{info}(e)=\Big(\bigoplus_{i}\bigodot_{e\in S_i}\operatorname{info}(e)\Big)\otimes\Big(\bigoplus_{j}\bigodot_{e\in T_j}\operatorname{info}(e)\Big)\)。用 \(f_i\) 表示 \(\bigodot_{e\in S_i}\operatorname{info}(e)\)，\(g_j\) 表示 \(\bigoplus_{j}\bigodot_{e\in T_j}\operatorname{info}(e)\)，上等式变成：\(\bigoplus_{i,j}\Big(f_i\odot g_j\Big)=\Big(\bigoplus_{i}f_i\Big)\otimes\Big(\bigoplus_{j}g_j\Big)\)。这个形式很像分配律，进一步，我们可以断言，当且仅当 \(\odot\) 对 \(\oplus\) 满足 分配律 时，\(\otimes\) 存在，且 \(\otimes\) 就是 \(\odot\) 本身，此时，\(\odot\) 和 \(\oplus\) 构成一个 半环。

例如，当 \(\odot=+\)，\(\oplus=\max\) 时，\(+\) 对 \(\max\) 满足分配律，此时 \(\otimes\) 存在，且 \(\otimes=\odot=+\)。实际图论意义也很好理解，\(u\rightarrow w\) 所有简单路径中的最长的长度，即为 \(u\rightarrow v\) 和 \(v\rightarrow w\) 分别找到两条最长的拼起来。当 \(\odot=\times\)，\(\oplus=+\) 时，\(\times\) 对 \(+\) 满足分配律，此时 \(\otimes\) 存在，且 \(\otimes=\odot=\times\)。当 \(\odot=\oplus=+\) 时，\(+\) 对 \(+\) 不满足分配律，我们找不到 \(\otimes\) 这个运算吗？若仅记录「边权相关信息」，我们确实找不到这样一个运算。但是在后文，我们通过扩展信息的方式，找到了维护这种信息的方式。

有了合并信息的方式，我们要考虑 「原子信息」 ，即小到不能再小的信息，此时就是 \(u,w\) 处在同一个点双的时候，我们不能找到一条连接 \(u,w\) 的简单路径通过某一个割点 \(v\)，于是不能通过合并信息的方式得到 \(u\rightarrow w\) 的信息。不妨对于处于同一点双中的 \(u,w\)，用 \(\operatorname{info}(u,w)\) 表示 \(u,w\) 之间的原子信息。原子信息通常是能够方便处理出来的。

我们已经学会了如何维护 \(\odot\) 对 \(\oplus\) 满足分配律的「边权相关信息」、「点权相关信息」。

类型二：非权值相关信息或 \(\odot=\oplus\) 的权值相关信息

此时只存在 \(\otimes\) 这个合并运算。预处理出原子信息同样通常是简单的。例如对于「简单路径条数」，\(\otimes\) 就是 \(\times\)。

上文中遗留一个问题，当 \(\odot=\oplus=+\) 时，由于 \(+\) 对其自身不具有分配律时，不能直接通过「边权相关信息」的方式维护。考虑扩展信息，设 \(\operatorname{info}(u,v)=(s,c)\)，其中 \(s\) 表示所求的「所有简单路径长度之和」，\(c\) 表示 \(u\rightarrow v\) 简单路径条数。我们惊喜地发现，有 \((s_1,c_1)\otimes(s_2,c_2)=(s_1c_2+s_2c_1,c_1\cdot c_2)\)，这是可以维护的！式子的意义是，对于每一条 \(p_i(u,v)\)，由于有 \(c_2\) 条 \(p_j(v,w)\)，所以 \(s_1\) 会贡献 \(c_2\) 次。

推广到到一般情况，当 \(\odot=\oplus\) 且对自身不具有分配律时，由于 \(\oplus\) 具有交换律，那么 \(\odot\) 也具有交换律，我们总是可以多记录一个 \(c\)，有 \((s_1,c_1)\otimes(s_2,c_2)=\Big((\odot_{c_2}(s_1))\odot(\odot_{c_1}(s_2)),c_1\cdot c_2\Big)\)，其中 \(\odot_{k}(x)=\underbrace{x\odot x\odot\cdots\odot x}_{k\text{ 个 }x}\)。

还有另一种可能需要维护的信息，即求能被任意一条 \(u\rightarrow v\) 简单路径经过的所有点 / 边的权值和，这个问题其实非常好处理，只需令 \(\otimes=\oplus\) 即可，这样就能统计到所有点 / 边的权值和，这和树上十分类似。

总结

以上几种信息，在处理完原子信息后，最后都是需要在一个个割点处，将信息通过 \(\otimes\) 合并起来，这正是圆方树可以解决的。

支持查询信息

让我们回到圆方树上，看看它对我们维护信息有什么帮助。

对于 \(u\rightarrow v\) 路径上的信息，可以将路径拆分成不断从一个点双走到另一个点双的过程，即 \(w_1 \stackrel{d_1}{\longrightarrow} w_2\stackrel{d_2}{\longrightarrow} w_3\stackrel{\cdots}{\longrightarrow} w_{m-1}\stackrel{d_{m-1}}{\longrightarrow}w_m\)，其中 \(w_1=u, w_m=v\)，对于 \(i=1,\ldots,m-1\)，\(w_{i},w_{i+1}\) 分别是编号为 \(d_i\) 的点双中两个点。根据上述讨论，我们要求的就是 \(\bigotimes\limits_{i=1}^{m-1}\operatorname{info}(w_i,w_{i+1})\)，而每个 \(\operatorname{info}(w_i,w_{i+1})\) 均为原子信息。

\(w_i\stackrel{d_i}{\longrightarrow}w_{i+1}\) 是走进一个点双，再从中走出来，圆方树上，我们为每个点双建立了一个方点，这不就相当于从 \(w_i\) 走到 \(d_i\) 对应的方点，再走到 \(w_{i+1}\) 吗？进一步地，这不就构成了圆方树上一条以 \(u,v\) 为端点的树链了吗？我们于是自然得出了圆方树和原图之间的对应关系：

1. 圆方树上一条「圆方圆」的路径，对应原图点双中两点之间所有简单路径。

   比如上图中 \(\{3,15,5\}\) 这条圆方圆路径，对应原图中 \(\{2,3,4,5\}\) 这个点双中以 \(3,5\) 为端点的所有简单路径，即 \(\{3,2,5\},\{3,4,5\}\) 两条简单路径。

   这就是进入一个点双，再从这个点双中走出来。

2. 圆方树上任意一条树链 \((u,v)\) 对应原无向图中 \(u,v\) 之间所有简单路径。

   比如上图中 \((3,8)\) 这条树链，对应了原图中 \(\{3,2,5,9,8\},\{3,2,5,6,9,8\},\{3,4,5,9,8\},\{3,4,5,6,9,8\}\) 这些简单路径。

   这种把每一条「圆方圆」的路径合并起来的过程，对应不断从一个点双走到另一个点双的过程。

圆方树很好地刻画了通过 \(\otimes\) 合并信息的过程！让我们继续分析。

对于一次查询 \((u,v)\)，设 \(p=\operatorname{lca}(u,v)\)，将树链拆分成 \(u\rightarrow p\rightarrow v\)。考虑 \(u\rightarrow p\) 一侧，另一侧类似。

考虑如下圆方树一部分：

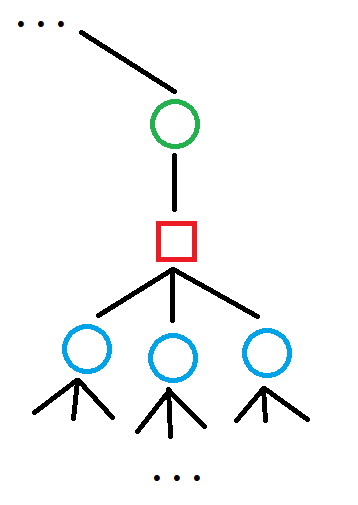
当我们经过某一个圆点（蓝点）\(u\)，跳向它爷爷（绿点）\(v\) 时，需要求的是 \(u\) 和 \(v\) 的原子信息 \(\operatorname{info}(u,v)\)。不考虑修改的情况下，每一次从 \(u\) 跳到 \(v\)，原子信息都是相同的，因为它的爷爷 \(v\) 是唯一的。我们于是这可以预处理出这些原子信息，而这类原子信息的个数和非根圆点个数相同，是 \(\mathcal{O}(n)\) 的。我们将 \(u\) 和 \(v\) 的信息，放在 \(u\) 到它父亲方点（红点）的边权上，每个方点和它父亲圆点之间的边权设为单位元。那么我们考虑一对具有祖孙关系的节点，他们之间的信息，便是圆方树上他们之间边权按序合并的结果。

对于 \(u\rightarrow p\) 和 \(p\rightarrow v\) 两段，根据我们赋的边权，和我们之前学过的树上信息维护方式，这两段路径的信息已经可以求出。对于不满足交换律的信息，可能需要维护向上跳的信息和向下跳的信息。接下来，好像直接把这两个信息合并起来就是对的，其实不然。对于 \(p\) 是圆点的情况，这么做是正确的；但是对于 \(p\) 是方点的情况，设 \(u'\) 为 \(p\) 的孩子且是 \(u\) 的祖先，\(v'\) 同理，那么考虑直接合并信息的实际意义，是从 \(u\) 走到 \(u'\)，进入了 \(p\) 对应的点双，走到了 \(\operatorname{fa}(p)\)，再走进 \(p\) 对应的点双，走到 \(v'\)，最终到 \(v\)。这显然是错误的，我们要求 \(u'\rightarrow v'\) 的原子信息 \(\operatorname{info}(u',v')\)，而非 \(\operatorname{info}(u',\operatorname{fa}(p))\otimes\operatorname{info}(\operatorname{fa}(p),v')\)。解决方式很简单，只需要特殊查询一次 \(u'\rightarrow v'\) 的原子信息，和之前两个信息合并。

在实现上，我们需要支持询问点双内两点之间的原子信息，那么这是否意味着需要为每个点记录其所在所有点双内的信息？如果真的需要，我们可以为每一个元素开 \(m+1\) 个 vector，其中 \(m\) 个 vector<> info 用来记录信息，\(1\) 个 vector<int> id 用来存所有 \(u\) 点双的编号，意为 \(u\) 在编号为 id[u][i] 的点双内对应的信息为 info[u][i]，对于查询 \(u\) 在编号为 \(x\) 的点双中的信息，先在 id[u] 中二分出 \(x\) 的下标，再拿这个下标去访问 info[u]。但是这是不必要的，这是因为我们的查询并不真的「任意」，而是只会查询一个圆点，在其父亲方点对应点双中的信息。而每个孩子圆点的父亲是唯一的，如果他被查询到，所用到的信息也是唯一的，那就不需要使用 vector 了。vector 的写法请参考下文仙人掌部分例五代码。

至此，我们借助圆方树的特殊结构，结合树上信息维护方式，通过 \(\otimes\) 的合并方式，可以查询给定点对间所有简单路径的信息。

支持修改信息

如果有了修改呢？树上我们使用树剖来支持修改查询树链信息，那么接下来要做的就是把圆方树剖开，尝试在上面维护信息。

先来考虑一种特殊的信息，求 \(u\rightarrow v\) 能到达的所有点的点权的信息和。这时候同一个点双内 \(u\rightarrow v\) 的信息为点双中除去 \(v\) 的点权信息和。发现圆方树上的边权很有规律，对于一个方点，它连向所有孩子圆点的边权总是相同的，都是该点双中除去父亲圆点的点权信息和。我们把边权上放，给方点一个点权（注意和原点权加以区分），为原先我们给圆方树赋的边权，再把圆点的点权设置为单位元。我们的查询似乎就变成了圆方树上路径的点权信息之和。

考虑在 LCA 处的特殊情况。若 LCA 为方点，同样需要得到 \(u'\rightarrow v'\) 的信息。如果严格遵循上文对原子信息的定义，我们需要先扣掉 \(v'\) 的点权，但是这样到最后会漏掉 \(v'\) 的点权（点权转换后的特殊情况），所以我们完全不必扣掉 \(v'\) 的点权，而是查出 LCA 的点权后，再加上 LCA 父亲圆点的点权。对于 LCA 为圆点的情况，我们统计漏了这个 LCA 圆点的信息，这把它的点权贡献到答案里就好了。如此就完成了查询。

修改某个点的权值的时候，除了需要维护仙人掌上每个点的点权，还要修改其在圆方树上父亲方点的点权。要想快速得到新的点权，要对每一个方点维护一个支持插入删除的数据结构，每次先删除原先的贡献，再加入修改后点权的贡献即可。

我们现在只需要在一棵树上，支持修改点权，询问 \(\operatorname{lca}\)，询问路径点权和。这个可以树剖做到 \(\log^2\)，或者可以做到单 \(\log\)。另外，理论上来说，我们还可以继续上放点权，也就是在圆树操作。但是这会造成很多边界情况，不优雅，故不展开讨论。

考虑更为一般的情况。我们发现边权上放的本质是为了修改的时候，能够将父亲方点的所有孩子圆点往上跳的边权都修改。但是真的一定需要更新每个孩子圆点吗？并不是，我们只需要修改重孩子圆点。每次跳重链时，只需要考虑链顶这个轻儿子的特殊情况。于是完成了修改和维护信息。

「圆树」：不设置方点的可行性

上文中，方点的作用仅是用来判断 \(u'\) 和 \(v'\) 是否在同一点双内，在一些简单的问题中，我们确实可以不建出方点，只建出「圆树」，并在每个点记录它在圆方树上父亲方点是谁，在查询的时候，只需要要找出 \(u',v'\)（如果存在的话），然后判断他们的父亲圆点是否相同，就能知道 LCA 是方点还是圆点。

优点

1. 节点总数为 \(n\)：

   不引入新的方点，整棵树的节点数量保持为原图大小的 \(n\)，在最坏情况下仅为传统圆方树节点数的一半。这样可以节省时间空间，而且不会因为手残数组开小，或者预处理只处理到 \(n\) 而红温。

2. 实现简单：

   若采用倍增算法来维护树上信息和求 LCA，当一个节点是另一个节点的祖先时，不会出现 LCA 是方点的特殊情况。剩下来的情况，我们倍增本来就是先求出了 \(u',v'\)，然后再跳最后一步到 LCA 的，那我们在跳之前判断一下就好了，不必等到跳了才发现是同一个方点。

缺点

1. 过度依赖倍增：
   若题目采用树上前缀和、差分等方式来维护信息，通常使用基于 DFS 序的 \(\mathcal{O}(1)\) LCA 算法，而寻找 \(u', v'\) 却是 \(\mathcal{O}(\log n)\) 的，导致效率不匹配。除非你愿意使用如长链剖分实现 \(\mathcal{O}(1)\) 的 kth-father 查询：先求出 LCA，再通过深度差计算 \(u'\) 或 \(v'\)，这会显著增加代码复杂度。

   发明了基于 DFS 序 \(\mathcal{O}(1)\) 求 \(u',v'\) 的算法，可见：博客。

2. 在特定情况下有过多边界问题：

   例如维护需要支持修改的信息，使用圆树将需要很多分类讨论，万一没有讨论所有情况，就会出错，而且代码将变得难以理解。

3. 过于小众：
   求调的时候别人说看不懂。

---

总而言之，这是仅是一种小优化，在掌握了圆方树的基本构造与思想后，读者可根据题目类型与实现习惯，自行选择是否采用此优化版本。

圆树和圆方树两种写法，在例题五和例题十三均分别给出，供参考对比。

圆方树在「仙人掌」上的应用

我们先从 仙人掌 这种特殊的无向图开始研究圆方树，这是因为仙人掌具有十分良好的性质。

初识仙人掌

仙人掌的定义

仙人掌指任意一条边最多出现在一个简单环中的无向连通图。

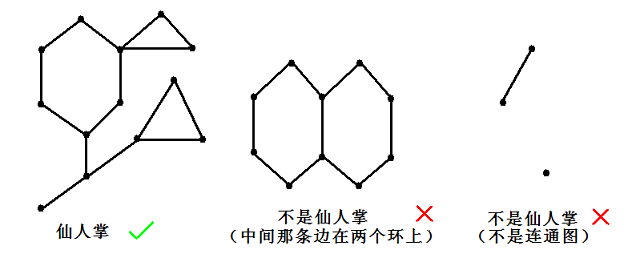
仙人掌的性质

1. 仙人掌边数上界为 \(\mathcal{O}(n)\)。

   准确来说，为 \(2n-2\) 或 \(\lfloor\frac{3}{2}(n-1)\rfloor\)。

   当允许重边时，把一棵树的所有 \(n-1\) 条树边，复制一遍，得到一棵 \(2n-2\) 条边的仙人掌。注意不可能出现三条重边连接两个点，否则就不满足仙人掌的定义了。

   当不允许重边时，可以发现如下「类菊花」的结构使得边数达到最多，为 \(\lfloor\frac{3}{2}(n-1)\rfloor\)。

   

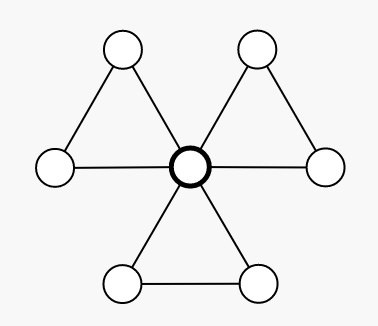
2. 仙人掌具有类似树的结构。

   我们发现，由于仙人掌的环不交（准确的说为边不交），这使得其保留了树的一些形态。

   把每一个环看做一个巨大的节点，仙人掌就成了一棵树了，只不过有些节点间不依靠边相连，而是在公共点处相切。

   类似树上「子树」，我们可以定义「子仙人掌」。
   「子仙人掌」

   指定一个根，定义 \(u\) 的「子仙人掌」为，断开根和 \(u\) 的所有简单路径的边后，\(u\) 所在的连通块。

   不难发现，\(u\) 的「子仙人掌」对应圆方树上 \(u\) 的子树。画个图就十分清晰了：

   

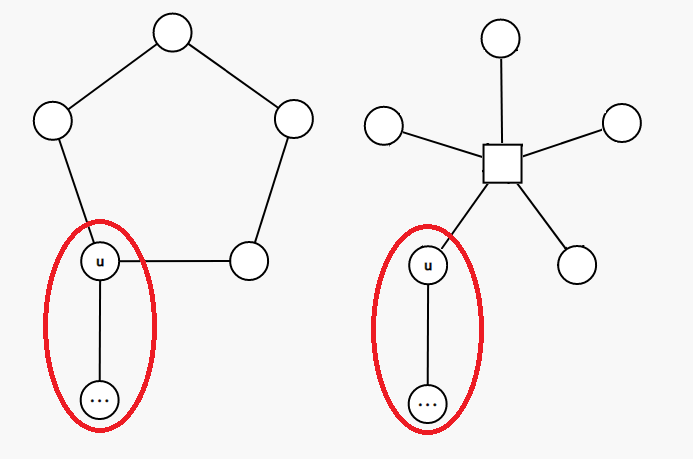
   不难做进一步推广，类似在一般无向图上定义「子无向图」，容易发现，这同样对应圆方树的子树。

   类似树上「树链」，在 只存在奇环 的仙人掌上，由于最长 / 短路唯一，我们可以定义「长链」、「短链」的概念。
   「长链」、「短链」

   \(u,v\) 之间经过边数最多的的简单路径称为 \(u,v\) 间的「长链」；\(u,v\) 之间经过边数最少的简单路径称为 \(u,v\) 间的「短链」。

   显然，在仙人掌中每经过一个环时，若都选择在环上走最长（或最短）路径 ，则整条走出的路径即为 \(u, v\) 间的长链（或短链）。

需要注意仙人掌上的点双并 不一定是环，通过一条不在环上的边连接的两个点，构成了两个点的点双，而这个点双不是一个环。有时候我们需要特判这种情况。

仙人掌上构造圆方树

我们可能需要在构造圆方树的时候，维护当前环的形态，即得到当前环对应的子图。

方法一：树上前缀和

一种做法是，对每个节点维护在 tarjan 的 dfs 树上的树上前缀和（即到根的信息），对于在 dfs 树上 \(u\) 是 \(v\) 的祖先，用 \(v\) 的前缀和减去 \(u\) 的前缀和，就能得到 \(u\) 到 \(v\) 之间的信息。那我们选用父亲圆点 \(u\) 作为环首，这样环上每一个点都处于 dfs 树中 \(u\) 的子树中，于是可以得到每个点到环首 \(u\) 的信息。至于总环长，发现我们上述过程考虑的是一条以 \(u\) 为环首的一条链，对于环尾 \(v\)，他有且仅有一条返祖边，且这条返祖边恰连向 \(u\)，从而构成一个环。一个点不可能有两条或以上返祖边，否则不满足仙人掌的定义。而这个返祖边我们可以轻松维护。如下图，蓝色的边为 dfs 树树边，红色的边为返祖边，细黑边为圆方树上的树边。当前的环即为若干条蓝边和一条红边构成的环。绿色箭头表示环首走向环尾的方向，蓝紫色箭头指向形成闭环的那条环尾指向环首的边。

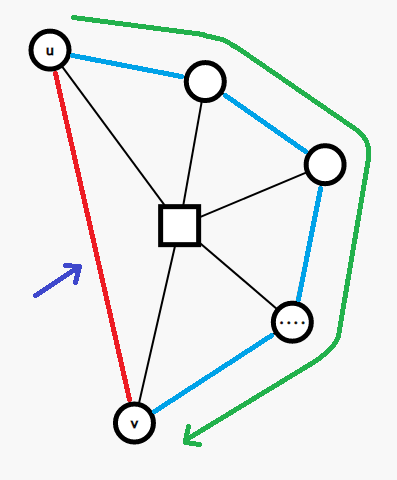
方法二：弹边栈

这种做法对于不可差分信息不太好处理，并且依赖于环这种形态，不好向一般点双拓展。考虑类似点的栈，维护一个边的栈，存返祖边和树边，在 tarjan 的过程中，每次找到一个点双（\(\operatorname{low}(v) \geq \operatorname{dfn}(u)\)），就不断弹栈，直到弹出连接 \(u,v\) 的树边 （注意必须是树边）。这个过程中弹出的边，便构成了这个点双的子图。对于复杂一些的点双，我们需要建出这个子图，然后在这个子图上跑一些算法，但是于仙人掌而言，我们把一个环建出来再处理，未免小题大做了。我们发现按照弹栈的顺序，弹出的边依次为环中的返祖边，深度最深的树边，深度次深的树边，直到 \(u,v\) 之间的树边。更加优雅的做法是，我们按照弹栈的顺序，假设当前弹出的边为 \(u'\rightarrow v'\)，边权为 \(w\)，并且不是连接 \(u,v\) 的树边，设 \(u\) 在环上的信息前缀和为 \(p_u\)，那么就让 \(p_{u'}\gets p_{v'}+w\)。这种方法下，环首为 \(u\)，环尾是 \(v\)，\(u,v\) 之间的树边成了环尾连向环首的边。如下图。事实上，使用了这种方式，我们不需要原先的点栈，每次弹出的边的起点，相当于原先点栈每次弹出的点。

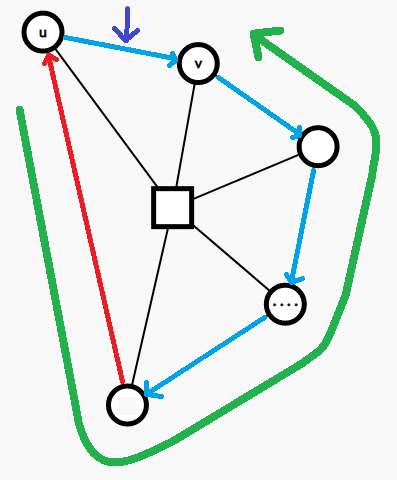
类型一：单次询问整体信息

计数类问题

在处理计数类问题时，往往需要借助圆方树进行类似树形 DP，或其他类似树上的统计方法。

在普通树上，这类问题我们已非常熟悉；放到基环树上，常见的技巧是将环上 DP 与树形 DP 分开处理，其本质原因是，把环上每个结点看做对应树根，这棵树是一个子问题，所以剩下的部分是一个环上问题。

在仙人掌上，由于我们前文提到的仙人掌具有的类似树的性质，所以在 DP 转移的时候，可以分环上 DP 和树形 DP 进行转移，或者按照环上和树上进行统计答案。这在圆方树上体现为，在方点、圆点上分别处理。

实际上，对于这类问题，我们甚至无需显式构建整棵圆方树。只需在分析与转移过程中设想当前所处的是圆点还是方点，并据此决定转移逻辑，即可完成建模与求解。这也是圆方树思想灵活而强大的体现。
例一、静态仙人掌最大独立集（小 C 的独立集，黑暗爆炸、洛谷、Hydro） Problem Statement

给你一个有 \(n\) 个点和 \(m\) 条边的仙人掌，求它的最大独立集大小。

\(n\leq 5\times 10^4\)，\(m\leq 6\times 10^4\)。
Problem Analysis

树上最大独立集是经典的（猜你想找：没有上司的舞会），我们设 \(f_{u,0/1}\) 表示以 \(u\) 为根的子树这个子问题，\(u\) 选 / 不选，最大独立集为多少。转移为 \(f_{u,0}=\sum\limits_{v\in\operatorname{son}(u)}\max\Big\{f_{v,0},f_{v,1}\Big\}\)，\(f_{u,1}=\operatorname{val}(u)+\sum\limits_{v\in\operatorname{son}(u)}f_{v,0}\)。

基环树上最大独立集是经典的（猜你想找：MAFIJA，ZJOI2008 骑士），我们先把树形 DP 跑了，得到环上每个点 \(u\) 的 \(f_{u,0/1}\)，然后再做一遍环上 DP。如果这个环没有首尾之间的独立集限制，这其实就是一条链，按照树的方式转移即可。但是首尾之间有限制，我们就先钦定首必不能选，然后做一遍 DP，把尾的 \(f_{0/1}\) 算到答案的贡献里，然后钦定首必选（亦可钦定其可选可不选，如果需要求独立集方案，为了不冲不漏，此处要钦定必选），再做一遍 DP，把尾的 \(f_0\) 贡献进去，这里就不贡献 \(f_1\) 了，不然会不满足首尾之间的限制条件。
另外一种基环树 DP 形式

有人说，我学的基环树 DP 不太一样，是：把环上一条边拎出来，剩下一棵树，然后类似上面的钦定，做两遍树形 DP。这两种方法其实是本质相同的，只不过这种方法把断边后的环当做树上一条链，整体做一遍 DP，相当于把环上 DP 放在树形 DP 里做了。对于仙人掌来说，我们还是喜欢单独对环做 DP。

那么仙人掌上也很好做了。\(f\) 的定义便是关于 \(u\) 的子仙人掌上的信息。圆点上我们赋初值 \(f_{u,0}\gets 0, f_{u,1}\gets 1\)。在方点上，我们做环上 DP，然后把答案统计到方点的父亲圆点 \(u\) 上。先使得 \(u\) 在环尾，然后类似基环树上的环做两遍 DP，得到 \(f_{u,0/1}\)。在两遍环上的 DP 的时候，不要把答案直接赋给 \(f_u\)，而是应该使用临时变量存放，做完两遍 DP 后再存到 \(f_u\) 里面，这样是为了避免第一次 DP 对第二次 DP 造成的影响。

于是，我们做到了时空线性 \(\mathcal{O}(n+m)\) 解决了本题。

---

做完这题可以去尝试一下 SDOI2010 城市规划，树套环上求至少间隔两个位置的最大独立集，可以参考我的题解。
Solution

#include <cstdio>
#include <iostream>
#include <vector>
using namespace std;

const int N = 5e4 + 10;
const int M = 6e4 + 10;

int n, m;

struct node {
    int v, nxt;
} edge[M << 1];
int head[N], tot = 1;
void add(int u, int v) {
    edge[++tot] = { v, head[u] };
    head[u] = tot;
}

int dfn[N], low[N], timer;
int stack[N], top;

int f[N][2], g[N][2];

void tarjan(int u, int fr) {
    f[u][1] = 1, f[u][0] = 0;  // 圆点直接赋初值
    dfn[u] = low[u] = ++timer;
    stack[++top] = u;
    for (int i = head[u]; i; i = edge[i].nxt) {
        if (i == (fr ^ 1)) continue;
        int v = edge[i].v;
        if (!dfn[v]) {
            tarjan(v, i);
            low[u] = min(low[u], low[v]);
            if (low[v] >= dfn[u]) {
                // 这里应该会新建一个方点
                // 但我们并不需要真的把圆方树建出来
                
                vector<int> scc;
                while (true) {
                    int x = stack[top--];
                    scc.emplace_back(x);
                    if (x == v) break;
                }
                scc.emplace_back(u);   // u 在环尾
                
                int m = scc.size();
                int f0 = 0, f1 = 0;
                
                // 强制首不选
                g[0][0] = f[scc[0]][0], g[0][1] = -0x3f3f3f3f;
                for (int i = 1; i < m; ++i) {
                    g[i][0] = max(g[i - 1][0], g[i - 1][1]) + f[scc[i]][0];
                    g[i][1] = g[i - 1][0] + f[scc[i]][1];
                }
                f0 = max(f0, g[m - 1][0]);
                f1 = max(f1, g[m - 1][1]);
                
                // 首可选可不选
                g[0][0] = f[scc[0]][0], g[0][1] = f[scc[0]][1];
                for (int i = 1; i < m; ++i) {
                    g[i][0] = max(g[i - 1][0], g[i - 1][1]) + f[scc[i]][0];
                    g[i][1] = g[i - 1][0] + f[scc[i]][1];
                }
                f0 = max(f0, g[m - 1][0]);
                
                f[u][0] = f0, f[u][1] = f1;
            }
        } else {
            low[u] = min(low[u], dfn[v]);
        }
    }
}

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1, u, v; i <= m; ++i) {
        scanf("%d%d", &u, &v);
        add(u, v), add(v, u);
    }
    tarjan(1, 0);
    printf("%d", max(f[1][0], f[1][1]));
    return 0;
}

从最简单的树开始思考，然后想想基环树怎么处理，最后思考仙人掌上的问题，是我们处理此类问题的一般模式。这是由 \(0\) 个环，到 \(1\) 个环，再到若干个环，不断加强问题的过程。
例二、静态仙人掌直径（SHOI2008 仙人掌图，黑暗爆炸、洛谷、Hydro） Problem Statement

给你一个有 \(n\) 个点和 \(m\) 条边的仙人掌，求它的直径。直径被定义为两点间最短距离的最大值。

\(n\leq 5\times 10^4\)，\(m\leq 10^7\)。
Problem Analysis

树的直径是经典的（猜你想找：Longest path in a tree）。我们有两种解法，一种是两遍 DFS，但是它碰到负权边就挂了，而且不太具有可拓展性；另一种解法是树形 DP，记 \(f_u\) 表示从 \(u\) 开始往叶子的方向走，最长距离是多少，枚举 \(v\in \operatorname{son}(u)\)，先贡献答案 \(D\Leftarrow f_u+f_v+1\)，再做 DP \(f_u\Leftarrow f_v+1\)。（其中 \(a\Leftarrow b\) 表示 \(a\gets\max\{a,b\}\)。）

基环树求直径是经典的（猜你想找：IOI 2008 Island，NOI2013 快餐店，但是需要说明的是，这两题形式和本题相同，但是对直径的定义都略有不同，以下按照本题的定义分析）。先跑树形 DP，该贡献答案的贡献到答案里去，然后得到环上每一个点的 \(f\)，考虑一条经过环边的路径，设 \(\{c_m\}\) 表示这个环，那么这条路径形如：\(u \stackrel{\displaystyle f_{c_i}}{\longrightarrow} c_i \stackrel{w(i,j)}{\longrightarrow} c_j \stackrel{\displaystyle f_{c_j}}{\longrightarrow} v\)，其中 \(w(i,j)\) 表示环上第 \(i\) 个点到第 \(j\) 个点之间的最短距离，即为 \(\min\Big\{j-i,m-(j-i)\Big\}\)。考虑怎么求出 \(f_{c_i}+w(i,j)+f_{c_j}\) 的最大值。我们先拆换成链，再复制一份接在后面。枚举 \(i\) 和小于它的 \(j\)，强制让 \(w(j,i)\) 就等于 \(i-j\)，此时 \(j\) 需要满足的条件为 \(i-j\leq m-(i-j)\) 即 \(j\geq i-\lfloor m/2\rfloor\)，如此，我们统计的信息就是 \(\max\limits_{j=i-\lfloor m/2\rfloor}^{i-1}\Big\{f_{c_j}-j\Big\}+i+f_{c_i}\)，滑动窗口最值，可以用单调队列维护。注意到，这样我们并不会漏掉某一种情况。

那么仙人掌求直径也是简单的。我们在方点统计完答案的贡献后，还要处理出方点的父亲圆点 \(u\) 的 \(f\) 值，这个直接枚举环上另一个点 \(v\) 就可以了。

时空复杂度 \(\mathcal{O}(n+m)\)。
Solution

#include <cstdio>
#include <iostream>
#include <vector>
using namespace std;

const int N = 5e4 + 10;
const int M = 1e7 + 10;

int n, m, ans;

struct node {
    int v, nxt;
} edge[M << 1];
int head[N], tot = 1;
void add(int u, int v) {
    edge[++tot] = { v, head[u] };
    head[u] = tot;
}

int dfn[N], low[N], timer;
int stack[N], top;

int f[N], g[N << 1], Q[N << 1];

void tarjan(int u, int fr) {
    f[u] = 0;
    dfn[u] = low[u] = ++timer;
    stack[++top] = u;
    for (int i = head[u]; i; i = edge[i].nxt) {
        if (i == (fr ^ 1)) continue;
        int v = edge[i].v;
        if (!dfn[v]) {
            tarjan(v, i);
            low[u] = min(low[u], low[v]);
            if (low[v] >= dfn[u]) {
                vector<int> scc;
                while (true) {
                    int x = stack[top--];
                    scc.emplace_back(x);
                    if (x == v) break;
                }
                scc.emplace_back(u);
                int m = scc.size();
                
                for (int j = 0; j < m; ++j)
                    g[j] = g[j + m] = f[scc[j]];
                
                int head = 0, tail = -1;
                for (int j = 0; j < m << 1; ++j) {
                    while (head <= tail && Q[head] < j - m/2) ++head;
                    if (head <= tail) ans = max(ans, g[Q[head]] - Q[head] + j + g[j]);
                    while (head <= tail && g[Q[tail]] - Q[tail] <= g[j] - j) --tail;
                    Q[++tail] = j;
                }
                
                for (int j = 0; j < m - 1; ++j)
                    f[u] = max(f[u], f[scc[j]] + min(j + 1, m - j - 1));
            }
        } else {
            low[u] = min(low[u], dfn[v]);
        }
    }
}

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1, k; i <= m; ++i) {
        scanf("%d", &k);
        for (int u = 0, v; k--; u = v) {
            scanf("%d", &v);
            if (u) add(u, v), add(v, u);
        }
    }
    tarjan(1, 0);
    printf("%d", ans);
    return 0;
}

通过这两道板子题，相信你已经对静态仙人掌上全局问题的求解有了清晰的认识。

以上，我们了解了静态仙人掌上统计全局信息的方法。尽管我们并没有把圆方树建出来，我们还是可以想象在一棵虚拟的圆方树上求解问题：在一个方点上，处理这环上的信息，把孩子圆点的信息合并到父亲圆点中去；在一个圆点上，我们赋 DP 初值。这也是标题中「一种关于点双连通分量的思考方式」的体现，我们解题可能不需要圆方树，但是思考过程会借助圆方树方便思考。

所有路径类问题

如果你需要统计所有路径的信息，树上我们可能需要用到点分治。那么在仙人掌上，我们要对圆方树进行点分治，类似于树上，对于一个点统计经过这个点的信息。理论上来说点分树也可以被应用在仙人掌上。

由于作者还没有学习到 FFT，例题暂时不能完成，这部分暂且不展开。

所有「子仙人掌」类问题

树上这类问题我们有 树上启发式合并（DSU on tree） 的做法，也可以使用线段树合并优化。

根据结论，子仙人掌对应圆方树的子树，问题就被放到圆方树上，真的成了一棵树上的问题了。
例三、persistent DSU on cactus（洛谷） Problem Statement

\(n\) 个点 \(m\) 条边的仙人掌，每个结点有一个颜色 \(c_u\)。

\(q\) 次询问 \((u,k)\)，求 \(u\) 的子仙人掌中出现次数不小于 \(k\) 的颜色的颜色编号和。

\(u\) 的子仙人掌被定义为：断开在 \(1,u\) 所有简单路径上出现过的边后，\(u\) 所在的连通块。

不知道为什么出题的时候出成了强制在线。只要空间复杂度别太离谱就行。

\(2\leq n\leq10^5\)。\(1\leq q\leq 10^5\)。\(k\leq n\)。\(c_u\in1,n\)。
Problem Analysis

离线 DSU on tree，时间复杂度两只 \(\log\)，如果强制在线，其实就是需要树状数组的在每一个结点上的版本。换成一个可以支持：继承、单点修改、区间查询的数据结构，就是主席树。
Solution Code

#include <cstdio>
#include <iostream>
using namespace std;

const int N = 1e5 + 10;
const int M = N * 2;
const int NN = N * 2;

int n, m, q, c[N], O;

template <size_t _N, size_t _M>
class Graph {
public:
    Graph(): tot(1) {}
    struct node {
        int v, nxt;
    } edge[_M];
    int head[_N], tot;
    void add(int u, int v) {
        edge[++tot] = { v, head[u] };
        head[u] = tot;
    }
};

Graph<N, M << 1> G;
Graph<NN, NN> T;

namespace $build {

int dfn[N], low[N], timer;
int stack[N], top;
int dcc_cnt;

void tarjan(int u, int fr) {
    dfn[u] = low[u] = ++timer;
    stack[++top] = u;
    for (int i = G.head[u]; i; i = G.edge[i].nxt) {
        if (i == (fr ^ 1)) continue;
        int v = G.edge[i].v;
        if (!dfn[v]) {
            tarjan(v, i);
            low[u] = min(low[u], low[v]);
            if (low[v] >= dfn[u]) {
                ++dcc_cnt;
                T.add(u, dcc_cnt + n);
                while (true) {
                    int x = stack[top--];
                    T.add(dcc_cnt + n, x);
                    if (x == v) break;
                }
            }
        } else {
            low[u] = min(low[u], dfn[v]);
        }
    }
}

}

namespace $yzh {

const int M = N * 230;

struct node {
    int ls, rs;
    long long sum;
} tr[M];

int tot;
inline int copy(int u) {
    return tr[++tot] = tr[u], tot;
}

void modify(int& u, int l, int r, int p, int v) {
    tr[u = copy(u)].sum += v;
    if (l == r) return;
    int mid = (l + r) >> 1;
    if (p <= mid) modify(tr[u].ls, l, mid, p, v);
    else modify(tr[u].rs, mid + 1, r, p, v);
}

long long query(int u, int trl, int trr, int l, int r) {
    if (!u) return 0;
    if (l <= trl && trr <= r) return tr[u].sum;
    int mid = (trl + trr) >> 1;
    long long res = 0;
    if (l <= mid) res += query(tr[u].ls, trl, mid, l, r);
    if (r >  mid) res += query(tr[u].rs, mid + 1, trr, l, r);
    return res;
}

int combine(int u, int v) {
    if (!u || !v) return u | v;
    int o = copy(u);
    tr[o].sum += tr[v].sum;
    tr[o].ls = combine(tr[o].ls, tr[v].ls);
    tr[o].rs = combine(tr[o].rs, tr[v].rs);
    return o;
}

}

int dfn[NN], L[NN], R[NN], timer;
int siz[NN], son[NN];

void dfs(int u) {
    dfn[L[u] = ++timer] = u;
    siz[u] = 1;
    for (int i = T.head[u]; i; i = T.edge[i].nxt) {
        int v = T.edge[i].v;
        dfs(v);
        siz[u] += siz[v];
        if (siz[v] > siz[son[u]])
            son[u] = v;
    }
    R[u] = timer;
}

int cnt[N], rt[NN];

void sub(int l, int r) {
    for (int i = l; i <= r; ++i) {
        int u = dfn[i];
        if (u > n) continue;
        cnt[c[u]] -= 1;
    }
}

void add(int l, int r, int& rt) {
    for (int i = l; i <= r; ++i) {
        int u = dfn[i];
        if (u > n) continue;
        if (cnt[c[u]])
            $yzh::modify(rt, 1, n, cnt[c[u]], -c[u]);
        $yzh::modify(rt, 1, n, ++cnt[c[u]], c[u]);
    }
}

void redfs(int u) {
    for (int i = T.head[u]; i; i = T.edge[i].nxt) {
        int v = T.edge[i].v;
        if (v == son[u]) continue;
        redfs(v);
        sub(L[v], R[v]);
    }
    if (son[u]) redfs(son[u]), rt[u] = rt[son[u]];
    for (int i = T.head[u]; i; i = T.edge[i].nxt) {
        int v = T.edge[i].v;
        if (v == son[u]) continue;
        add(L[v], R[v], rt[u]);
    }
    add(L[u], L[u], rt[u]);
}

int main() {
    scanf("%d%d%d", &O, &n, &m);
    for (int i = 1; i <= n; ++i)
        scanf("%d", &c[i]);
    for (int i = 1, u, v; i <= m; ++i) {
        scanf("%d%d", &u, &v);
        G.add(u, v), G.add(v, u);
    }
    $build::tarjan(1, 0);
    dfs(1), redfs(1);
    scanf("%d", &q);
    for (long long u, k, lst = 0; q--; ) {
        scanf("%lld%lld", &u, &k);
        if (O) u ^= lst, k ^= lst;
        printf("%lld\n", lst = $yzh::query(rt[u], 1, n, k, n));
    }
    return 0;
}

Gen

#include <cstdio>
#include <iostream>
#include <vector>
#include <random>
#include <chrono>
#include <map>
#include <sstream>
#include <cstdio>
#include <iostream>
#include <vector>
using namespace std;

const int SEED = chrono::system_clock::now().time_since_epoch().count();

mt19937 rnd(SEED);

inline int rand(int l, int r) {
    if (l > r) throw "invalid range";
    return l + rnd() % (r - l + 1);
}

bool multiedge = true;
bool onlyOddCircle = false;

int n = rand(99000, 100000);

vector<pair<int, int>> edges;
vector<vector<int>> son(n, vector<int>());
vector<int> dpt(n);

int dfs(int u) {
    int res = u;
    int cnt = 0;
    for (size_t i = 0; i < son[u].size(); ++i) {
        int v = son[u][i];
        dpt[v] = dpt[u] + 1;
        int t = dfs(v);
        if (rand(0, son[u].size()) == 0)
            res = t;
        else if ((t != v || (multiedge && cnt < 2)) && ((dpt[t] - dpt[u] + 1) % 2 == 1 || !onlyOddCircle))
            edges.emplace_back(u, t), cnt += t == v;
    }
    return res;
}

std::ostringstream odata;

const int QSIZE = 1e5;

namespace $yzh {
void build(istringstream&);
vector<pair<pair<int, int>, long long>> qrys;
}

int main() {
    for (int i = 1; i < n; ++i) {
        int fa = rand(0, i - 1);
        edges.emplace_back(fa, i);
        son[fa].emplace_back(i);
    }
    dfs(0);
    for (size_t i = 1; i < edges.size(); ++i) {
        swap(edges[i], edges[rand(0, i)]);
    }
    
    int QJ = 1;
    
    odata << QJ << endl;
    
    int m = edges.size();
    
    odata << n << ' ' << m << endl;
    
    for (int i = 1; i <= n; ++i) odata << rand(1, 3) << " \n"[i == n];
    
    for (size_t i = 0; i < edges.size(); ++i) {
        int u = edges[i].first;
        int v = edges[i].second;
        if (rand(0, 1)) swap(u, v);
        odata << u + 1 << ' ' << v + 1 << endl;
    }
    
    auto _ = istringstream(odata.str());
    $yzh::build(_);
    
    auto& Q = $yzh::qrys;
    int q = Q.size();
    for (int i = 1; i < q; ++i)
        swap(Q[i], Q[rand(0, i)]);
    
    odata << q << endl;
    
    std::ostringstream oans;
    
    long long lstans = 0;
    for (auto [_, ans] : Q) {
        long long u = _.first, k = _.second;
        if (QJ) u ^= lstans, k ^= lstans;
        odata << u << ' ' << k << endl;
        oans << ans << endl;
        lstans = ans;
    }
    
    FILE* f = fopen("testdata\\10.in", "w");
    fprintf(f, "%s", odata.str().c_str());
    fclose(f);
    
    f = fopen("testdata\\10.ans", "w");
    fprintf(f, "%s", oans.str().c_str());
    fclose(f);
    
    
    fprintf(stderr, "SEED = %d\n", SEED);
    fprintf(stderr, "circle = %d\n", (int)edges.size() - (n - 1));
    fprintf(stderr, "n = %d, m = %d, q = %d\n", n, m, q);
    
    return 0;
}

namespace $yzh {

const int N = 1e5 + 10;
const int M = N * 2;
const int NN = N * 2;

int n, m, q, c[N];

template <size_t _N, size_t _M>
class Graph {
public:
    Graph(): tot(1) {}
    struct node {
        int v, nxt;
    } edge[_M];
    int head[_N], tot;
    void add(int u, int v) {
        edge[++tot] = { v, head[u] };
        head[u] = tot;
    }
};

Graph<N, M << 1> G;
Graph<NN, NN> T;

namespace $build {

int dfn[N], low[N], timer;
int stack[N], top;
int dcc_cnt;

void tarjan(int u, int fr) {
    dfn[u] = low[u] = ++timer;
    stack[++top] = u;
    for (int i = G.head[u]; i; i = G.edge[i].nxt) {
        if (i == (fr ^ 1)) continue;
        int v = G.edge[i].v;
        if (!dfn[v]) {
            tarjan(v, i);
            low[u] = min(low[u], low[v]);
            if (low[v] >= dfn[u]) {
                ++dcc_cnt;
                T.add(u, dcc_cnt + n);
                while (true) {
                    int x = stack[top--];
                    T.add(dcc_cnt + n, x);
                    if (x == v) break;
                }
            }
        } else {
            low[u] = min(low[u], dfn[v]);
        }
    }
}

}

long long ans[N];

int dfn[NN], L[NN], R[NN], timer;
int siz[NN], son[NN];

void dfs(int u) {
    dfn[L[u] = ++timer] = u;
    siz[u] = 1;
    for (int i = T.head[u]; i; i = T.edge[i].nxt) {
        int v = T.edge[i].v;
        dfs(v);
        siz[u] += siz[v];
        if (siz[v] > siz[son[u]])
            son[u] = v;
    }
    R[u] = timer;
}

namespace $yzh {

vector<pair<int, int>> qrys;

long long tr[N];
void modify(int p, int v) {
    for (; p; p &= p - 1)
        tr[p] += v;
}
long long query(int p) {
    long long res = 0;
    for (; p <= n; p += p & -p)
        res += tr[p];
    return res;
}

}

int cnt[N];

void add(int l, int r, int f) {
    for (int i = l; i <= r; ++i) {
        int u = dfn[i];
        if (u > n) continue;
        $yzh::modify(cnt[c[u]], -c[u]);
        $yzh::modify(cnt[c[u]] += f, c[u]);
    }
}

void redfs(int u) {
    for (int i = T.head[u]; i; i = T.edge[i].nxt) {
        int v = T.edge[i].v;
        if (v == son[u]) continue;
        redfs(v);
        add(L[v], R[v], -1);
    }
    if (son[u]) redfs(son[u]);
    for (int i = T.head[u]; i; i = T.edge[i].nxt) {
        int v = T.edge[i].v;
        if (v == son[u]) continue;
        add(L[v], R[v], 1);
    }
    add(L[u], L[u], 1);
    if (qrys.size() == QSIZE || u > n) return;
    int x = rand(0, 2);
    while (x) {
        int p = rand(1, 10);
        if ($yzh::query(p) == 0) continue;
        qrys.push_back({{ u, p }, $yzh::query(p) });
        --x;
        if (qrys.size() == QSIZE) return;
    }
}

void build(istringstream& is) {
    int o;
    is >> o;
    is >> n >> m;
    for (int i = 1; i <= n; ++i)
        is >> c[i];
    for (int i = 1, u, v; i <= m; ++i) {
        is >> u >> v;
        G.add(u, v), G.add(v, u);
    }
    $build::tarjan(1, 0);
    dfs(1);
    redfs(1);
}

}

分别以每个点为根求解

树上这类问题我们有 换根 DP 的做法，仙人掌上也可以类似做换根 DP。
例四、GAME on cactus（洛谷） Problem Statement

小 X 和小 Y 来到一棵 \(n\) 个点 \(m\) 条边的仙人掌上玩游戏，点编号为 \(1\sim n\)。

一开始某个节点上有个棋子，小 X 和小 Y 轮流移动这个棋子，已经走过的边不能再走，谁不能移动谁就输了。

小 Y 先手，她向你求助，对于每一个节点，若其作为初始放置棋子的节点，她是否有必胜策略？

\(2\leq n\leq2\times10^5\)。
Problem Analysis

见我的题解。
Solution Code

见我的题解。
Gen

#include <cstdio>
#include <iostream>
#include <vector>
#include <random>
#include <chrono>
using namespace std;

const int SEED = chrono::system_clock::now().time_since_epoch().count();

void _err(const char* msg, int lineNum) {
    fprintf(stderr, "Error at line #%d: %s\n", lineNum, msg);
    exit(1);
}
#define err(msg) _err(msg, __LINE__)

inline int rand(int l, int r) {
    static mt19937 rnd(SEED);
    if (l > r) err("invalid range");
    return l + rnd() % (r - l + 1);
}

vector<vector<int>> pts;
vector<pair<int, int>> edges;

int main() {
	int rem = rand(230990, 231000), o = 0;  // data may be wrong!
	int m = 0;
	pts.push_back({});
	while (rem > 0) {
		int x = rand(3, max(3, min(10, rem)));
		rem -= x;
		if (rem == 1) --rem, ++x;
		m++;
		vector<int> vec;
		if (m == 1) {
			for (int i = 1; i <= x; ++i)
				vec.emplace_back(++o);
		} else {
			int fa = rand(1, max(1, m - 20));
			auto& y = pts[fa];
			int t = rand(0, (int)y.size() - 1);
			vec.emplace_back(y[t]);
			for (int i = 2; i <= x; ++i)
			 	vec.emplace_back(++o);
		}
		for (int i = 2; i <= x; ++i)
			edges.emplace_back(vec[i - 2], vec[i - 1]);
		edges.emplace_back(vec[x - 1], vec[0]);
		pts.emplace_back(vec);
	}
	
	int n = o;
	
    vector<int> id(n);
    for (int i = 0; i < n; ++i) id[i] = i;
    for (int i = 1; i < n; ++i)
        swap(id[i], id[rand(0, i)]);
	
	for (size_t i = 1; i < edges.size(); ++i)
        swap(edges[i], edges[rand(0, i)]);
    
    printf("%d %d\n", o, (int)edges.size());
    for (size_t i = 0; i < edges.size(); ++i) {
        int u = edges[i].first;
        int v = edges[i].second;
        if (rand(0, 1)) swap(u, v);
        u = id[u - 1], v = id[v - 1];
        printf("%d %d\n", u + 1, v + 1);
    }
	
	return 0;
}

#include <cstdio>
#include <iostream>
#include <vector>
#include <random>
#include <chrono>
using namespace std;

/* =========== Parameter =========== */

const int SEED = chrono::system_clock::now().time_since_epoch().count();

bool multiedge = true;
bool onlyOddCircle = false;

int MULTI_P = 50;

/* =========== Parameter =========== */

void _err(const char* msg, int lineNum) {
    fprintf(stderr, "Error at line #%d: %s\n", lineNum, msg);
    exit(1);
}
#define err(msg) _err(msg, __LINE__)

inline int rand(int l, int r) {
    static mt19937 rnd(SEED);
    if (l > r) err("invalid range");
    return l + rnd() % (r - l + 1);
}

int n = rand(199990, 200000);
int LEN = rand(1314, 1324);

int m_limit = -1;  // -1 for not limit

vector<pair<int, int>> edges;
vector<vector<int>> son(n, vector<int>());
vector<int> dpt(n);

int maxcir = LEN;
int chong = 0;

void dfs(int u) {
    for (size_t i = 0; i < son[u].size(); ++i) {
        int v = son[u][i];
        dpt[v] = dpt[u] + 1;
        dfs(v);
    }
}

int redfs(int u, int ban, vector<int>& vec) {
    vec.emplace_back(u);
    int res = u;
    for (size_t i = 0; i < son[u].size(); ++i) {
        int v = son[u][i];
        if (v == ban) continue;
        int t = redfs(v, -1, vec);
        int len = dpt[t] - dpt[u] + 1;
        if ((t != v || (multiedge && rand(0, MULTI_P) == 0))
                && (len % 2 == 1 || !onlyOddCircle)
                && (m_limit == -1 || (int)edges.size() < m_limit))
            edges.emplace_back(u, t), maxcir = max(maxcir, len), chong += t == v;
        else if (/* res == u ||  */rand(0, son[u].size()) == 0 || dpt[t] > dpt[res])
            res = t;
    }
    return res;
}

int main() {
    // freopen(".\\testdata\\4.in", "w", stdout);
    
    // freopen("yzh", "w", stdout);
    // freopen("in", "w", stdout);
    
    if (n < 1) err("n shouldn't be less than 1");
    if (m_limit != -1 && m_limit < n - 1)
        err("m_limit shouldn't less than n-1");
    if (LEN > n)
        err("LEN too long");
    
    vector<int> id(n);
    for (int i = 0; i < n; ++i) id[i] = i;
    for (int i = 1; i < n; ++i)
        swap(id[i], id[rand(0, i)]);
    
    for (int i = 1; i < LEN; ++i) {
        int fa = i - 1;
        edges.emplace_back(fa, i);
        son[fa].emplace_back(i);
    }
    for (int i = LEN; i < n; ++i) {
        // int fa = rand(0, i - 1);
        int fa = rand(max(0, i - 20), i - 1);
        edges.emplace_back(fa, i);
        son[fa].emplace_back(i);
    }
    if (LEN > 1 && m_limit != n - 1) {
        edges.emplace_back(0, LEN - 1);
    }
    dfs(0);
    vector<int> son[n];
    for (int i = 1; i < LEN; ++i)
        redfs(i - 1, i, son[i - 1]);
    redfs(LEN - 1, -1, son[LEN - 1]);
    
    for (size_t i = 1; i < edges.size(); ++i)
        swap(edges[i], edges[rand(0, i)]);
    
    printf("%d %d\n", n, (int)edges.size());
    for (size_t i = 0; i < edges.size(); ++i) {
        int u = edges[i].first;
        int v = edges[i].second;
        if (rand(0, 1)) swap(u, v);
        u = id[u], v = id[v];
        printf("%d %d\n", u + 1, v + 1);
    }
    
    fprintf(stderr, "Success!\n");
    fprintf(stderr, "n = %d, m = %d\n", n, (int)edges.size());
    fprintf(stderr, "circle = %d\n", (int)edges.size() - (n - 1));
    fprintf(stderr, "maxcir = %d\n", maxcir);
    fprintf(stderr, "chong = %d\n", chong);
    return 0;
}

类型二：静态仙人掌，维护点对间所有简单路径信息

这类问题需要我们支持：修改点权或边权，询问点对之间路径上信息。
例五、仙人掌点对间最短路长度（【模板】静态仙人掌，洛谷） Problem Statement

给你一个有 \(n\) 个点和 \(m\) 条边的仙人掌，和 \(q\) 组询问，每次询问两点 \(u,v\) 间最短路长度。

\(n\leq 10^4\)，\(m\leq 2\times 10^4\)，\(q\leq 10^4\)。
Problem Analysis

属于「边权相关信息」，\(\odot=+\)，\(\oplus=\min\)，\(+\) 对 \(\min\) 有分配律，可以求解。

对于原子信息的求解，我们需要对每个点双维护总环长，对于每个圆点维护，他在他父亲方点代表的环中，到环首的距离。

对于前文提到过的不是环的点双，特殊处理成一个环即可。

于是，我们可以在 \(\mathcal{O}\Big(m+(n+q)\log n\Big)\) 或者长链剖分优化求 kth-father \(\mathcal{O}(n\log n + q+m)\) 的时间复杂度内求解问题。
Solution

均采用倍增维护树上信息。
正常圆方树，采用树上前缀和预处理信息

#include <cstdio>
#include <iostream>
#include <vector>
using namespace std;

const int N = 1e4 + 10;
const int M = 2e4 + 10;
const int lg2N = __lg(N << 1) + 1;

int n, m, q;

template <size_t _N, size_t _M>
class Graph {
public:
    Graph(): tot(1) {}
    struct node {
        int v, w, nxt;
    } edge[_M];
    int head[_N], tot;
    void add(int u, int v, int w) {
        edge[++tot] = { v, w, head[u] };
        head[u] = tot;
    }
};

Graph<N, M << 1> G;
Graph<N << 1, N << 1> T;  // 圆方树

int dfn[N], low[N], timer;
int stack[N], top;

int pre[N];  // dfs 树的树上前缀和
int rev[N];  // 返祖边边权
int dis[N];  // 在父亲方点代表的点双中，到环首的距离

int dcc_cnt;
int cirsum[N];  // 环的总环长

inline int query(int u, int v, int x) {
    // u, v 在编号为 x 的点双中的距离
    int d = abs(dis[u] - dis[v]);
    return min(d, cirsum[x] - d);
}

void tarjan(int u, int fr) {
    dfn[u] = low[u] = ++timer;
    stack[++top] = u;
    for (int i = G.head[u]; i; i = G.edge[i].nxt) {
        if (i == (fr ^ 1)) continue;
        int v = G.edge[i].v, w = G.edge[i].w;
        if (!dfn[v]) {
            pre[v] = pre[u] + w;
            tarjan(v, i);
            low[u] = min(low[u], low[v]);
            if (low[v] >= dfn[u]) {
                ++dcc_cnt;
                cirsum[dcc_cnt] = pre[stack[top]] - pre[u] + rev[stack[top]];
                if (stack[top] == v)
                    cirsum[dcc_cnt] <<= 1;
                T.add(u, dcc_cnt + n, 0);
                while (true) {
                    int x = stack[top--];
                    dis[x] = pre[x] - pre[u];
                    T.add(dcc_cnt + n, x, min(dis[x], cirsum[dcc_cnt] - dis[x]));
                    if (x == v) break;
                }
            }
        } else {
            low[u] = min(low[u], dfn[v]);
            if (dfn[v] < dfn[u])
                rev[u] = w;
        }
    }
}

int dpt[N << 1];
int fa[lg2N][N << 1];
int sum[lg2N][N << 1];

void dfs(int u) {
    for (int i = T.head[u]; i; i = T.edge[i].nxt) {
        int v = T.edge[i].v, w = T.edge[i].w;
        fa[0][v] = u;
        sum[0][v] = w;
        dpt[v] = dpt[u] + 1;
        dfs(v);
    }
}

int query(int u, int v) {
    int ans = 0;
    if (dpt[u] < dpt[v]) swap(u, v);
    for (int i = lg2N - 1; ~i; --i)
        if (fa[i][u] && dpt[fa[i][u]] >= dpt[v]) {
            ans += sum[i][u];
            u = fa[i][u];
        }
    if (u == v) return ans;
    for (int i = lg2N - 1; ~i; --i)
        if (fa[i][u] != fa[i][v]) {
            ans += sum[i][u] + sum[i][v];
            u = fa[i][u], v = fa[i][v];
        }
    // 此时 u,v 即为 u',v'
    int p = fa[0][u];  // lca
    if (p <= n)  // lca 为圆点
        ans += sum[0][u] + sum[0][v];  // 这一行其实没有作用，因为 sum[0][u]=sum[0][v]=0
    else
        ans += query(u, v, p - n);
    return ans;
}

int main() {
    scanf("%d%d%d", &n, &m, &q);
    for (int i = 1, u, v, w; i <= m; ++i) {
        scanf("%d%d%d", &u, &v, &w);
        G.add(u, v, w), G.add(v, u, w);
    }
    tarjan(1, 0);
    dfs(1);
    for (int k = 1; k < lg2N; ++k)
        for (int i = 1; i <= n + dcc_cnt; ++i) {
            fa[k][i] = fa[k - 1][fa[k - 1][i]];
            sum[k][i] = sum[k - 1][i] + sum[k - 1][fa[k - 1][i]];
        }
    for (int u, v; q--; ) {
        scanf("%d%d", &u, &v);
        printf("%d\n", query(u, v));
    }
    return 0;
}

正常圆方树，采用弹边栈预处理信息

#include <cstdio>
#include <iostream>
#include <vector>
using namespace std;

const int N = 1e4 + 10;
const int M = 2e4 + 10;
const int lg2N = __lg(N << 1) + 1;

int n, m, q;

template <size_t _N, size_t _M>
class Graph {
public:
    Graph(): tot(1) {}
    struct node {
        int v, w, nxt;
    } edge[_M];
    int head[_N], tot;
    void add(int u, int v, int w) {
        edge[++tot] = { v, w, head[u] };
        head[u] = tot;
    }
};

Graph<N, M << 1> G;
Graph<N << 1, N << 1> T;  // 圆方树

int dfn[N], low[N], timer;
int stack[M], top;  // 注意这里的边栈的数组大小

int dis[N];  // 在父亲方点代表的点双中，到环首的距离

int dcc_cnt;
int cirsum[N];  // 环的总环长

inline int query(int u, int v, int x) {
    // u, v 在编号为 x 的点双中的距离
    int d = abs(dis[u] - dis[v]);
    return min(d, cirsum[x] - d);
}

void tarjan(int u, int fr) {
    dfn[u] = low[u] = ++timer;
    for (int i = G.head[u]; i; i = G.edge[i].nxt) {
        if (i == (fr ^ 1)) continue;
        int v = G.edge[i].v;
        if (!dfn[v]) {
            stack[++top] = i;
            tarjan(v, i);
            low[u] = min(low[u], low[v]);
            if (low[v] >= dfn[u]) {
                static int tmp[N];
                int tot = 0;
                ++dcc_cnt;
                while (true) {
                    int j = stack[top--];
                    int uu = G.edge[j ^ 1].v;
                    int vv = G.edge[j].v;
                    int w = G.edge[j].w;
                    cirsum[dcc_cnt] += w;
                    if (j == i) break;
                    dis[uu] = dis[vv] + w;
                    tmp[++tot] = uu;
                }
                if (tot == 0) {
                    tmp[++tot] = v;
                    dis[v] = cirsum[dcc_cnt];
                    cirsum[dcc_cnt] <<= 1;
                }
                T.add(u, dcc_cnt + n, 0);
                for (int j = 1; j <= tot; ++j) {
                    int x = tmp[j];
                    T.add(dcc_cnt + n, x, min(dis[x], cirsum[dcc_cnt] - dis[x]));
                }
            }
        } else {
            low[u] = min(low[u], dfn[v]);
            if (dfn[v] < dfn[u])
                stack[++top] = i;
        }
    }
}

int dpt[N << 1];
int fa[lg2N][N << 1];
int sum[lg2N][N << 1];

void dfs(int u) {
    for (int i = T.head[u]; i; i = T.edge[i].nxt) {
        int v = T.edge[i].v, w = T.edge[i].w;
        fa[0][v] = u;
        sum[0][v] = w;
        dpt[v] = dpt[u] + 1;
        dfs(v);
    }
}

int query(int u, int v) {
    int ans = 0;
    if (dpt[u] < dpt[v]) swap(u, v);
    for (int i = lg2N - 1; ~i; --i)
        if (fa[i][u] && dpt[fa[i][u]] >= dpt[v]) {
            ans += sum[i][u];
            u = fa[i][u];
        }
    if (u == v) return ans;
    for (int i = lg2N - 1; ~i; --i)
        if (fa[i][u] != fa[i][v]) {
            ans += sum[i][u] + sum[i][v];
            u = fa[i][u], v = fa[i][v];
        }
    // 此时 u,v 即为 u',v'
    int p = fa[0][u];  // lca
    if (p <= n)  // lca 为圆点
        ans += sum[0][u] + sum[0][v];  // 这一行其实没有作用，因为 sum[0][u]=sum[0][v]=0
    else
        ans += query(u, v, p - n);
    return ans;
}

int main() {
    scanf("%d%d%d", &n, &m, &q);
    for (int i = 1, u, v, w; i <= m; ++i) {
        scanf("%d%d%d", &u, &v, &w);
        G.add(u, v, w), G.add(v, u, w);
    }
    tarjan(1, 0);
    dfs(1);
    for (int k = 1; k < lg2N; ++k)
        for (int i = 1; i <= n + dcc_cnt; ++i) {
            fa[k][i] = fa[k - 1][fa[k - 1][i]];
            sum[k][i] = sum[k - 1][i] + sum[k - 1][fa[k - 1][i]];
        }
    for (int u, v; q--; ) {
        scanf("%d%d", &u, &v);
        printf("%d\n", query(u, v));
    }
    return 0;
}

不设置方点的圆树

#include <cstdio>
#include <iostream>
#include <vector>
using namespace std;

const int N = 1e4 + 10;
const int M = 2e4 + 10;
const int lgN = __lg(N) + 1;

int n, m, q;

template <size_t _N, size_t _M>
class Graph {
public:
    Graph(): tot(1) {}
    struct node {
        int v, w, nxt;
    } edge[_M];
    int head[_N], tot;
    void add(int u, int v, int w) {
        edge[++tot] = { v, w, head[u] };
        head[u] = tot;
    }
};

Graph<N, M << 1> G;
Graph<N, N> T;  // 不设置方点的圆树

int dfn[N], low[N], timer;
int stack[N], top;

int pre[N];  // dfs 树的树上前缀和
int rev[N];  // 返祖边边权
int dis[N];  // 在父亲方点代表的点双中，到环首的距离

int dcc_cnt;
int cirsum[N];  // 环的总环长

int tfa[N];  // 父亲方点对应的点双编号

inline int query(int u, int v, int x) {
    // u, v 在编号为 x 的点双中的距离
    int d = abs(dis[u] - dis[v]);
    return min(d, cirsum[x] - d);
}

void tarjan(int u, int fr) {
    dfn[u] = low[u] = ++timer;
    stack[++top] = u;
    for (int i = G.head[u]; i; i = G.edge[i].nxt) {
        if (i == (fr ^ 1)) continue;
        int v = G.edge[i].v, w = G.edge[i].w;
        if (!dfn[v]) {
            pre[v] = pre[u] + w;
            tarjan(v, i);
            low[u] = min(low[u], low[v]);
            if (low[v] >= dfn[u]) {
                ++dcc_cnt;
                cirsum[dcc_cnt] = pre[stack[top]] - pre[u] + rev[stack[top]];
                if (stack[top] == v)
                    cirsum[dcc_cnt] <<= 1;
                while (true) {
                    int x = stack[top--];
                    dis[x] = pre[x] - pre[u];
                    tfa[x] = dcc_cnt;
                    T.add(u, x, min(dis[x], cirsum[dcc_cnt] - dis[x]));
                    if (x == v) break;
                }
            }
        } else {
            low[u] = min(low[u], dfn[v]);
            if (dfn[v] < dfn[u])
                rev[u] = w;
        }
    }
}

int dpt[N];
int fa[lgN][N];
int sum[lgN][N];

void dfs(int u) {
    for (int i = T.head[u]; i; i = T.edge[i].nxt) {
        int v = T.edge[i].v, w = T.edge[i].w;
        fa[0][v] = u;
        sum[0][v] = w;
        dpt[v] = dpt[u] + 1;
        dfs(v);
    }
}

int query(int u, int v) {
    int ans = 0;
    if (dpt[u] < dpt[v]) swap(u, v);
    for (int i = lgN - 1; ~i; --i)
        if (fa[i][u] && dpt[fa[i][u]] >= dpt[v]) {
            ans += sum[i][u];
            u = fa[i][u];
        }
    if (u == v) return ans;
    for (int i = lgN - 1; ~i; --i)
        if (fa[i][u] != fa[i][v]) {
            ans += sum[i][u] + sum[i][v];
            u = fa[i][u], v = fa[i][v];
        }
    // 此时 u,v 即为 u',v'
    if (tfa[u] != tfa[v])
        ans += sum[0][u] + sum[0][v];  // 这一行现在就必要了
    else
        ans += query(u, v, tfa[u]);
    return ans;
}

int main() {
    scanf("%d%d%d", &n, &m, &q);
    for (int i = 1, u, v, w; i <= m; ++i) {
        scanf("%d%d%d", &u, &v, &w);
        G.add(u, v, w), G.add(v, u, w);
    }
    tarjan(1, 0);
    dfs(1);
    for (int k = 1; k < lgN; ++k)
        for (int i = 1; i <= n; ++i) {
            fa[k][i] = fa[k - 1][fa[k - 1][i]];
            sum[k][i] = sum[k - 1][i] + sum[k - 1][fa[k - 1][i]];
        }
    for (int u, v; q--; ) {
        scanf("%d%d", &u, &v);
        printf("%d\n", query(u, v));
    }
    return 0;
}

正常圆方树，使用 vector 处理信息

#include <cstdio>
#include <iostream>
#include <vector>
#include <cassert>
#include <algorithm>
using namespace std;

const int N = 1e4 + 10;
const int M = 2e4 + 10;
const int lg2N = __lg(N << 1) + 1;

int n, m, q;

template <size_t _N, size_t _M>
class Graph {
public:
    Graph(): tot(1) {}
    struct node {
        int v, w, nxt;
    } edge[_M];
    int head[_N], tot;
    void add(int u, int v, int w) {
        edge[++tot] = { v, w, head[u] };
        head[u] = tot;
    }
};

Graph<N, M << 1> G;
Graph<N << 1, N << 1> T;  // 圆方树

int dfn[N], low[N], timer;
int stack[N], top;

int pre[N];  // dfs 树的树上前缀和
int rev[N];  // 返祖边边权

vector<int> idx[N];
vector<int> dis[N];

int dcc_cnt;
int cirsum[N];  // 环的总环长

inline int query(int u, int v, int x) {
    // u, v 在编号为 x 的点双中的距离
    int ku = lower_bound(idx[u].begin(), idx[u].end(), x) - idx[u].begin();
    int kv = lower_bound(idx[v].begin(), idx[v].end(), x) - idx[v].begin();
    assert(idx[u][ku] == x && idx[v][kv] == x);
    int d = abs(dis[u][ku] - dis[v][kv]);
    return min(d, cirsum[x] - d);
}

void tarjan(int u, int fr) {
    dfn[u] = low[u] = ++timer;
    stack[++top] = u;
    for (int i = G.head[u]; i; i = G.edge[i].nxt) {
        if (i == (fr ^ 1)) continue;
        int v = G.edge[i].v, w = G.edge[i].w;
        if (!dfn[v]) {
            pre[v] = pre[u] + w;
            tarjan(v, i);
            low[u] = min(low[u], low[v]);
            if (low[v] >= dfn[u]) {
                ++dcc_cnt;
                cirsum[dcc_cnt] = pre[stack[top]] - pre[u] + rev[stack[top]];
                if (stack[top] == v)
                    cirsum[dcc_cnt] <<= 1;
                idx[u].push_back(dcc_cnt);
                dis[u].push_back(0);
                T.add(u, dcc_cnt + n, 0);
                while (true) {
                    int x = stack[top--];
                    idx[x].push_back(dcc_cnt);
                    dis[x].push_back(pre[x] - pre[u]);
                    T.add(dcc_cnt + n, x, query(u, x, dcc_cnt));
                    if (x == v) break;
                }
            }
        } else {
            low[u] = min(low[u], dfn[v]);
            if (dfn[v] < dfn[u])
                rev[u] = w;
        }
    }
}

int dpt[N << 1];
int fa[lg2N][N << 1];
int sum[lg2N][N << 1];

void dfs(int u) {
    for (int i = T.head[u]; i; i = T.edge[i].nxt) {
        int v = T.edge[i].v, w = T.edge[i].w;
        fa[0][v] = u;
        sum[0][v] = w;
        dpt[v] = dpt[u] + 1;
        dfs(v);
    }
}

int query(int u, int v) {
    int ans = 0;
    if (dpt[u] < dpt[v]) swap(u, v);
    for (int i = lg2N - 1; ~i; --i)
        if (fa[i][u] && dpt[fa[i][u]] >= dpt[v]) {
            ans += sum[i][u];
            u = fa[i][u];
        }
    if (u == v) return ans;
    for (int i = lg2N - 1; ~i; --i)
        if (fa[i][u] != fa[i][v]) {
            ans += sum[i][u] + sum[i][v];
            u = fa[i][u], v = fa[i][v];
        }
    // 此时 u,v 即为 u',v'
    int p = fa[0][u];  // lca
    if (p <= n)  // lca 为圆点
        ans += sum[0][u] + sum[0][v];  // 这一行其实没有作用，因为 sum[0][u]=sum[0][v]=0
    else
        ans += query(u, v, p - n);
    return ans;
}

int main() {
    scanf("%d%d%d", &n, &m, &q);
    for (int i = 1, u, v, w; i <= m; ++i) {
        scanf("%d%d%d", &u, &v, &w);
        G.add(u, v, w), G.add(v, u, w);
    }
    tarjan(1, 0);
    dfs(1);
    for (int k = 1; k < lg2N; ++k)
        for (int i = 1; i <= n + dcc_cnt; ++i) {
            fa[k][i] = fa[k - 1][fa[k - 1][i]];
            sum[k][i] = sum[k - 1][i] + sum[k - 1][fa[k - 1][i]];
        }
    for (int u, v; q--; ) {
        scanf("%d%d", &u, &v);
        printf("%d\n", query(u, v));
    }
    return 0;
}

接下来看有修改的问题。

对于前文分析的特殊点权相关信息，由于其对于仙人掌的形态没有要求，所以将在无向图部分例题十四给出一种实现方式。
例六、BUY on cactus（洛谷） Problem Statement

小 Y 来到一棵 \(n\) 个点 \(m\) 条边的仙人掌上旅游，并希望通过买卖赚差价，点编号为 \(1\sim n\)。

在一次旅游时，她告诉你旅游的起点和终点 \(u,v\)。她会选择一条以 \(u,v\) 为端点的简单路径 ，并在路上选择一个结点 \(u'\)，花费 \(c_{u'}\) 的代价购入某个物品，再选择一个结点 \(v'\)，以 \(w_{v'}\) 的价格卖出，获得 \(w_{v'}-c_{u'}\) 的利润。显然她必须先购入才能卖出，但 \(u'\) 可以等于 \(v'\)。她不能啥也不做。小 Y 问你，在最优计划下，她能够获得的利润最大值，这个值可能为负。

由于这棵仙人掌很不稳定，每一个点的 \(c_u,w_u\) 都可能发生变化。你需要支持这种修改的同时，能够回答小 Y 的问题。具体来说，总共有 \(q\) 次修改或询问。

\(2\leq n\leq2\times10^5\)，\(1\leq q\leq 10^5\)。
Problem Analysis

购买类问题是十分经典的，我们就做过静态树上的问题：POJ-3728 The merchant。

需要维护的信息是什么？千万不要矩阵学傻了，说需要维护矩阵。我们可以维护三元组 \((\mathrm{mic},\mathrm{mxw},\mathrm{ans})\)，分别表示 minimum cost, maximum value and answer（最小花费、最大收益和路上的答案）。树上我们只需要考虑拼接两条简单路径的情况，有：

\\\begin{matrix} (\\mathrm{mic}_1,\\mathrm{mxw}_1,\\mathrm{ans}_1)+(\\mathrm{mic}_2,\\mathrm{mxw}_2,\\mathrm{ans}_2)\\\\ \\Downarrow\\\\ \\Big(\\min\\{\\mathrm{mic}_1,\\mathrm{mic}_2\\},\\max\\{\\mathrm{mxw}_1,\\mathrm{mxw}_2\\},\\max\\{\\mathrm{ans}_1,\\mathrm{ans}_2,\\mathrm{mxw}_2-\\mathrm{mic}_1\\}\\Big) \\end{matrix} \\

一步一步来看看这个模型怎么放到仙人掌上。

首先对于每一个环，可以拉下来变成一个序列，容易得到每一个点，通过左链和右链到环顶的两个信息，注意潜在的信息合并顺序问题。我们需要将这两个信息或起来，而不是上文的 \(+\) 运算：

\\\begin{matrix} (\\mathrm{mic}_1,\\mathrm{mxw}_1,\\mathrm{ans}_1)\\cup(\\mathrm{mic}_2,\\mathrm{mxw}_2,\\mathrm{ans}_2)\\\\ \\Downarrow\\\\ \\Big(\\min\\{\\mathrm{mic}_1,\\mathrm{mic}_2\\},\\max\\{\\mathrm{mxw}_1,\\mathrm{mxw}_2\\},\\max\\{\\mathrm{ans}_1,\\mathrm{ans}_2\\}\\Big) \\end{matrix} \\

我们于是可以得到它与方点父亲之间的边权，注意潜在的方向问题。

其实已经解决了整个问题。修改的时候修改重儿子，查询的时候跳重链，链顶轻儿子特殊查询。可以参考示例代码。

时间复杂度：\(\mathcal{O}(m+n\log n+q\log^2n)\)。单次修改 \(\mathcal{O}(\log n)\)，单次查询 \(\mathcal{O}(\log^2n)\)。
Solution

#include <cstdio>
#include <iostream>
#include <cstring>
#include <vector>
#include <cassert>
using namespace std;

const int N = 5e5 + 10;
const int M = 1e6 + 10;
const int N2 = N << 1;

const int inf = 0x3f3f3f3f;

int n, m, q;
int c[N], w[N];

struct node {
    int mic, mxw, a1, a2;
    void init(int c, int w) {
        mic = c, mxw = w;
        a1 = a2 = w - c;
    }
    void unit() {
        mic = inf, mxw = -inf;
        a1 = a2 = -inf;
    }
    friend inline node operator + (const node& a, const node& b) {
        node c;
        c.mic = min(a.mic, b.mic);
        c.mxw = max(a.mxw, b.mxw);
        c.a1 = max(a.a1, b.a1);
        c.a2 = max(a.a2, b.a2);
        c.a1 = max(c.a1, b.mxw - a.mic);
        c.a2 = max(c.a2, a.mxw - b.mic);
        return c;
    }
    friend inline node operator | (const node& a, const node& b) {
        node c;
        c.mic = min(a.mic, b.mic);
        c.mxw = max(a.mxw, b.mxw);
        c.a1 = max(a.a1, b.a1);
        c.a2 = max(a.a2, b.a2);
        return c;
    }
    inline node rev() const {
        return { mic, mxw, a2, a1 };
    }
};
inline node gen(int c, int w) {
    node r;
    r.init(c, w);
    return r;
}

template <size_t _N, size_t _M>
class Graph {
public:
    Graph(): tot(1) {}
    struct node {
        int v, nxt;
    } edge[_M];
    int head[_N], tot;
    void add(int u, int v) {
        edge[++tot] = { v, head[u] };
        head[u] = tot;
    }
};

Graph<N, M << 1> G;
Graph<N2, N2> T;

int dcc_cnt;

namespace $build {

int dfn[N], low[N], timer;
int stack[N], top;

void tarjan(int u, int fr) {
    dfn[u] = low[u] = ++timer;
    stack[++top] = u;
    for (int i = G.head[u]; i; i = G.edge[i].nxt) {
        if (i == (fr ^ 1)) continue;
        int v = G.edge[i].v;
        if (!dfn[v]) {
            tarjan(v, i);
            low[u] = min(low[u], low[v]);
            if (low[v] >= dfn[u]) {
                ++dcc_cnt;
                T.add(u, dcc_cnt + n);
                while (true) {
                    int x = stack[top--];
                    T.add(dcc_cnt + n, x);
                    if (x == v) break;
                }
            }
        } else {
            low[u] = min(low[u], dfn[v]);
        }
    }
}

}

class Segment_Tree {
private:
    struct _node {
        int ls, rs;
        node v;
    };
    vector<_node> buf;
    int n, rt[2], tot;
#define ls buf[u].ls
#define rs buf[u].rs
    inline void pushup(int u, bool f) {
        if (f)
            buf[u].v = buf[rs].v + buf[ls].v;
        else
            buf[u].v = buf[ls].v + buf[rs].v;
    }
    void _build(int& u, int l, int r, node val[], bool f) {
        u = ++tot;
        if (l == r) {
            if (f)
                buf[u].v = val[l].rev();
            else
                buf[u].v = val[l];
            return;
        }
        int mid = (l + r) >> 1;
        _build(ls, l, mid, val, f);
        _build(rs, mid + 1, r, val, f);
        pushup(u, f);
    }
    void _upd(int u, int l, int r, int p, node v, bool f) {
        if (l == r) {
            if (f)
                buf[u].v = v.rev();
            else
                buf[u].v = v;
            return;
        }
        int mid = (l + r) >> 1;
        if (p <= mid) _upd(ls, l, mid, p, v, f);
        else _upd(rs, mid + 1, r, p, v, f);
        pushup(u, f);
    }
    node query(int u, int trl, int trr, int l, int r) {
        if (l <= trl && trr <= r) return buf[u].v;
        int mid = (trl + trr) >> 1;
        if (r <= mid)
            return query(ls, trl, mid, l, r);
        if (l > mid)
            return query(rs, mid + 1, trr, l, r);
        return query(ls, trl, mid, l, r) + query(rs, mid + 1, trr, l, r);
    }
    node query_rev(int u, int trl, int trr, int l, int r) {
        if (l <= trl && trr <= r) return buf[u].v;
        int mid = (trl + trr) >> 1;
        if (r <= mid)
            return query_rev(ls, trl, mid, l, r);
        if (l > mid)
            return query_rev(rs, mid + 1, trr, l, r);
        return query_rev(rs, mid + 1, trr, l, r) + query_rev(ls, trl, mid, l, r);
    }
#undef ls
#undef rs
public:
    void build(int _n, node val[]) {
        n = _n, rt[0] = rt[1] = 0, tot = 0;
        buf.resize(n * 4 + 10);
        _build(rt[0], 1, n, val, 0);
        _build(rt[1], 1, n, val, 1);
    }
    void upd(int p, node v) {
        assert(1 <= p && p <= n);
        _upd(rt[0], 1, n, p, v, 0);
        _upd(rt[1], 1, n, p, v, 1);
    }
    node query(int l, int r) {
        assert(1 <= l && l <= r && r <= n);
        return query(rt[0], 1, n, l, r);
    }
    node query_rev(int l, int r) {
        assert(1 <= l && l <= r && r <= n);
        return query_rev(rt[1], 1, n, l, r);
    }
};

using tree_t = Segment_Tree;

int siz[N2], son[N2];
int fa[N2], top[N2], dpt[N2];
int idx[N2], dfn[N2], timer;
int bl[N], cir[N];

tree_t tr[N], yzh;

node getfa(int u) {
    int v = fa[u];
    assert(v != 0 && v > n);
    int m = cir[v - n];
    node L = tr[v - n].query(1, bl[u]);
    node R = tr[v - n].query_rev(bl[u], m);
    return L | R;
}

node getfa_rev(int u) {
    return getfa(u).rev();
}

node __val[N2];
void dfs(int u) {
    siz[u] = 1;
    for (int i = T.head[u]; i; i = T.edge[i].nxt) {
        int v = T.edge[i].v;
        fa[v] = u;
        dpt[v] = dpt[u] + 1;
        dfs(v), siz[u] += siz[v];
        if (siz[v] > siz[son[u]])
            son[u] = v;
    }
    if (u > n) {
        static node tmp[N];
        int m = 0;
        for (int i = T.head[u]; i; i = T.edge[i].nxt) {
            int v = T.edge[i].v;
            tmp[++m].init(c[v], w[v]);
            bl[v] = m;
        }
        cir[u - n] = m;
        tr[u - n].build(m, tmp);
    }
}

void redfs(int u, int tp) {
    top[u] = tp;
    dfn[idx[u] = ++timer] = u;
    if (u == tp || u > n)
        __val[idx[u]].unit();
    else
        __val[idx[u]] = getfa(u);
    if (son[u]) redfs(son[u], tp);
    for (int i = T.head[u]; i; i = T.edge[i].nxt) {
        int v = T.edge[i].v;
        if (v == son[u]) continue;
        redfs(v, v);
    }
}

node qcir(int u, int v) {
    assert(fa[u] == fa[v]);
    int p = fa[u];
    assert(p != 0 && p > n);
    assert(u != v);
    int bu = bl[u], bv = bl[v];
    int m = cir[p - n];
    if (bu <= bv) {
        node A = tr[p - n].query(bu, bv);
        node B = tr[p - n].query_rev(1, bu) + gen(c[fa[p]], w[fa[p]]) + tr[p - n].query_rev(bv, m);
        return A | B;
    } else {
        node A = tr[p - n].query_rev(bv, bu);
        node B = tr[p - n].query(bu, m) + gen(c[fa[p]], w[fa[p]]) + tr[p - n].query(1, bv);
        return A | B;
    }
}

int query(int u, int v) {
    int lu = 0, lv = 0;
    node L, R;
    L.unit(), R.unit();
    while (top[u] != top[v]) {
        if (dpt[top[u]] < dpt[top[v]]) {
            if (lv && lv <= n) R = getfa(lv) + R;
            R = yzh.query(idx[top[v]], idx[v]) + R;
            lv = top[v];
            v = fa[top[v]];
        } else {
            if (lu && lu <= n) L = L + getfa_rev(lu);
            L = L + yzh.query_rev(idx[top[u]], idx[u]);
            lu = top[u];
            u = fa[top[u]];
        }
    }
    if (u == v) {
        if (u <= n) {
            if (lu && lu <= n) L = L + getfa_rev(lu);
            if (lv && lv <= n) R = getfa(lv) + R;
            L = L + gen(c[u], w[u]);
        } else {
            assert(lu != 0 && lv != 0);
            L = L + qcir(lu, lv);
        }
    } else if (dpt[u] > dpt[v]) {
        if (v <= n) {
            if (lu && lu <= n) L = L + getfa_rev(lu);
            if (lv && lv <= n) R = getfa(lv) + R;
            L = L + yzh.query_rev(idx[v] + 1, idx[u]);
            L = L + gen(c[v], w[v]);
        } else {
            if (lu && lu <= n) L = L + getfa_rev(lu);
            assert(lv != 0);
            if (idx[v] + 2 <= idx[u])
                L = L + yzh.query_rev(idx[v] + 2, idx[u]);
            L = L + qcir(dfn[idx[v] + 1], lv);
        }
    } else {
        if (u <= n) {
            if (lu && lu <= n) L = L + getfa_rev(lu);
            if (lv && lv <= n) R = getfa(lv) + R;
            R = yzh.query(idx[u] + 1, idx[v]) + R;
            R = gen(c[u], w[u]) + R;
        } else {
            if (lv && lv <= n) R = getfa(lv) + R;
            assert(lu != 0);
            if (idx[u] + 2 <= idx[v])
                R = yzh.query(idx[u] + 2, idx[v]) + R;
            R = qcir(lu, dfn[idx[u] + 1]) + R;
        }
    }
    node ans = L + R;
    return ans.a1;
}

void modify(int u, int v, int t) {
    if (t == 0) c[u] = v;
    else w[u] = v;
    if (u != 1) {
        int p = fa[u];
        tr[p - n].upd(bl[u], gen(c[u], w[u]));
        int x = son[p];
        yzh.upd(idx[x], getfa(x));
    }
}

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1, u, v; i <= m; ++i) {
        scanf("%d%d", &u, &v);
        G.add(u, v), G.add(v, u);
    }
    for (int i = 1; i <= n; ++i)
        scanf("%d", &c[i]);
    for (int i = 1; i <= n; ++i)
        scanf("%d", &w[i]);
    $build::tarjan(1, 0);
    dfs(1);
    redfs(1, 1);
    yzh.build(n + dcc_cnt, __val);
    scanf("%d", &q);
    for (int op, u, v, t; q--; ) {
        scanf("%d%d%d", &op, &u, &v);
        if (op == 1) {
            printf("%d\n", query(u, v));
        } else {
            scanf("%d", &t);
            modify(u, v, t);
        }
    }
    return 0;
}

Gen

#include <cstdio>
#include <iostream>
#include <vector>
#include <random>
#include <chrono>
using namespace std;

/* =========== Parameter =========== */

const int SEED = chrono::system_clock::now().time_since_epoch().count();

bool multiedge = true;
bool onlyOddCircle = false;

int MULTI_P = 50;

/* =========== Parameter =========== */

void _err(const char* msg, int lineNum) {
    fprintf(stderr, "Error at line #%d: %s\n", lineNum, msg);
    exit(1);
}
#define err(msg) _err(msg, __LINE__)

inline int rand(int l, int r) {
    static mt19937 rnd(SEED);
    if (l > r) err("invalid range");
    return l + rnd() % (r - l + 1);
}

int n = rand(199990, 200000);
int q = rand(99990, 100000);
int LEN = rand(13140, 23240);

int m_limit = -1;  // -1 for not limit

vector<pair<int, int>> edges;
vector<vector<int>> son(n, vector<int>());
vector<int> dpt(n);

int maxcir = LEN;
int chong = 0;

void dfs(int u) {
    for (size_t i = 0; i < son[u].size(); ++i) {
        int v = son[u][i];
        dpt[v] = dpt[u] + 1;
        dfs(v);
    }
}

int redfs(int u, int ban, vector<int>& vec) {
    vec.emplace_back(u);
    int res = u;
    for (size_t i = 0; i < son[u].size(); ++i) {
        int v = son[u][i];
        if (v == ban) continue;
        int t = redfs(v, -1, vec);
        int len = dpt[t] - dpt[u] + 1;
        if ((t != v || (multiedge && rand(0, MULTI_P) == 0))
                && (len % 2 == 1 || !onlyOddCircle)
                && (m_limit == -1 || (int)edges.size() < m_limit))
            edges.emplace_back(u, t), maxcir = max(maxcir, len), chong += t == v;
        else if (rand(0, son[u].size()) == 0 || dpt[t] > dpt[res])
            res = t;
    }
    return res;
}

int main() {
    freopen(".\\testdata\\10.in", "w", stdout);
    
    // freopen("yzh", "w", stdout);
    // freopen("in", "w", stdout);
    
    if (n < 1) err("n shouldn't be less than 1");
    if (m_limit != -1 && m_limit < n - 1)
        err("m_limit shouldn't less than n-1");
    if (LEN > n)
        err("LEN too long");
    
    vector<int> id(n);
    for (int i = 0; i < n; ++i) id[i] = i;
    for (int i = 1; i < n; ++i)
        swap(id[i], id[rand(0, i)]);
    
    for (int i = 1; i < LEN; ++i) {
        int fa = i - 1;
        edges.emplace_back(fa, i);
        son[fa].emplace_back(i);
    }
    for (int i = LEN; i < n; ++i) {
        // int fa = rand(0, i - 1);
        int fa = rand(max(0, i - 20), i - 1);
        edges.emplace_back(fa, i);
        son[fa].emplace_back(i);
    }
    if (LEN > 1 && m_limit != n - 1) {
        edges.emplace_back(0, LEN - 1);
    }
    dfs(0);
    vector<int> son[n];
    for (int i = 1; i < LEN; ++i)
        redfs(i - 1, i, son[i - 1]);
    redfs(LEN - 1, -1, son[LEN - 1]);
    
    for (size_t i = 1; i < edges.size(); ++i)
        swap(edges[i], edges[rand(0, i)]);
    
    printf("%d %d\n", n, (int)edges.size());
    for (size_t i = 0; i < edges.size(); ++i) {
        int u = edges[i].first;
        int v = edges[i].second;
        if (rand(0, 1)) swap(u, v);
        u = id[u], v = id[v];
        printf("%d %d\n", u + 1, v + 1);
    }
    
    const int V = 5e8;
    
    for (int i = 1; i <= n; ++i)
        printf("%d%c", rand(-V, V), " \n"[i == n]);
    for (int i = 1; i <= n; ++i)
        printf("%d%c", rand(-V, V), " \n"[i == n]);
    
    printf("%d\n", q);
    for (int i = 1; i <= q; ++i) {
        int op = rand(1, 2);
        if (op == 1) {
            if (rand(0, 100) == 0) {
                int u = rand(1, n);
                int v = rand(1, n);
                printf("1 %d %d\n", u, v);
            } else {
                int uu = rand(0, LEN - 1 - 1);
                int vv = rand(uu + 1, LEN - 1);
                int u = son[uu][rand(0, (int)son[uu].size() - 1)];
                int v = son[vv][rand(0, (int)son[vv].size() - 1)];
                u = id[u] + 1;
                v = id[v] + 1;
                printf("1 %d %d\n", u, v);
            }
        } else {
            int u = rand(1, n);
            int v = rand(-V, V);
            int t = rand(0, 1);
            printf("2 %d %d %d\n", u, v, t);
        }
    }
    
    fprintf(stderr, "Success!\n");
    fprintf(stderr, "n = %d, m = %d\n", n, (int)edges.size());
    fprintf(stderr, "circle = %d\n", (int)edges.size() - (n - 1));
    fprintf(stderr, "maxcir = %d\n", maxcir);
    fprintf(stderr, "chong = %d\n", chong);
    return 0;
}

类型三：静态仙人掌，支持维护链和子仙人掌

回想我们树上树链剖分可以支持什么操作？树链、子树修改，树链、子树查询。那么由于仙人掌具有一定树的形态，我们也可以将仙人掌剖分，实现长链（短链）修改、子仙人掌查询。接下来考虑的信息均是点权。

回顾我们是如何定义仙人掌上的链的，以及不要忘记，在仙人掌中每经过一个奇环时，若始终选择在环上走最长（或最短）的路径，则整条走出的路径即为 \(u, v\) 间的长链（或短链）。

我们不妨先只考虑如何修改 \(u,v\) 间的长链。拆解问题，如果 \(p=\operatorname{lca}(u,v)\) 是个圆点，相当于修改 \(u\rightarrow p\) 和 \(p\rightarrow v\) 两条长链；否则 \(p\) 为方点，除了 \(u\rightarrow u'\) 和 \(v'\rightarrow v\) 这两个和 \(p\) 为圆点时形式相同的子问题，还有一个环上 \(u'\rightarrow v'\) 最长路的问题。

先考虑如何修改一对具有祖先关系的 \(u,v\) 之间的长链。树链剖分后，在圆方树上跳一段重链时，DFS 序上对应的连续一段区间为圆方树上这条重链。树上我们需要的正是一段连续的区间，因为这样我们就可以用数据结构来维护了，但在仙人掌上，这是不对的，我们要修改的不是这样一条圆方交错的圆方树树链，而是需要修改仙人掌上长链的每一个点。

我们不妨修改一下这个 DFS 序，使得对于这样连续一段区间，完整包含了我们需要修改的点。并且显然我们不需要方点出现在 DFS 序上，因为它身上没有我们需要维护的信息。

对于方点，我们先把其轻儿子放到 DFS 序后面，再放其重儿子，接着处理重儿子的子仙人掌，最后处理其他轻儿子的子仙人掌。从 DFS 序的角度上考虑，相当于把一个方点替换成了它的所有轻孩子，那么这个方点对应的环就完整地出现在了我们的区间上。

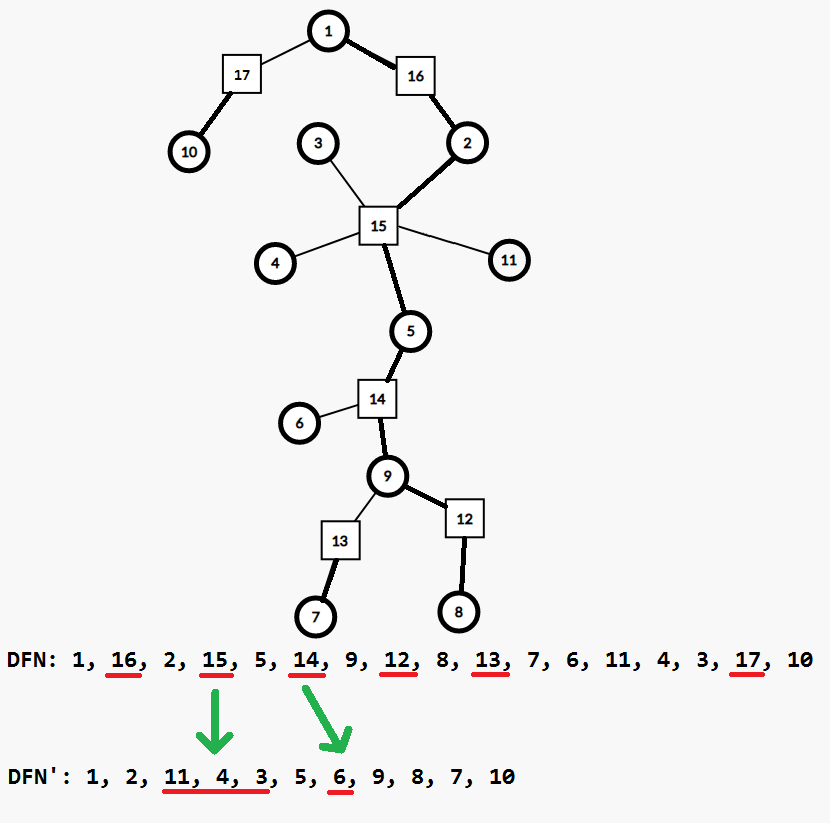
举个例子，比如 \(1\sim 9\) 这条重链，原先 DFS 序上对应区间为 \(1,7=\{1,16,2,15,5,14,9\}\)。而在修改后，方点 \(15\) 变为了其所有轻儿子 \(\{11,4,3\}\)，\(14\) 同理变成了 \(6\)，修改后的 DFS 序对应区间为 \(1,8=\{1,2,11,4,3,5,6,9\}\)，涵盖了 \(1\sim 9\) 长链上的所有点 \(\{1,2,3,4,5,6,9\}\)。

完整包含了还不够，我们还需要能够精准的修改想要修改的点。例如，例子中 \(11\) 点出现在了区间上，而它不在 \(1\sim 9\) 的长链上，这等价于它不在 \(2\sim 5\) 环上最长路径上。由于重儿子的唯一性，这启示我们将一个方点的所有轻儿子分类，分为「在重儿子到父亲圆点（原图上）的最长路上」和「在重儿子到父亲圆点（原图上）的最短路上」两种类型，这是方便处理出来的。例如，\(11\) 属于后者，而 \(3,4\) 属于前者。现在我们区间上有三种类型的圆点，因为不要忘了重儿子也是一种圆点。每次我们只需要将对应类型的轻孩子，和所有重儿子修改就行了。这个是可以用线段树维护的。

至此，我们通过修改 DFS 序，和使用线段树的区间分类修改操作，完成了「修改一段重链对应原仙人掌上的长 / 短链」。

仔细思考一下，在将其推广到一对具有祖孙关系的节点的链修改时，还有细节没有处理。重链拆分后，对于 \(v\rightarrow u\) 这条重链（\(v\) 是链顶），当 \(u\) 为圆点且 \(v\) 为方点时，根据上面讨论，对应区间为 \(v\) 第一个轻儿子在 DFS 序的位置，到 \(u\) 在 DFS 序中的位置。当 \(v\) 也为圆点时，我们不能将区间左端点设为 \(v\) 在 DFS 序中的位置，如下图：

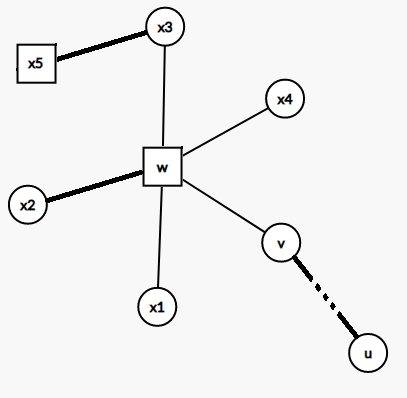
它的 DFS 序如下：

\x_3,\\colorbox{#409eff}{$ (x_5) $},\\colorbox{#409eff}{$ x_4,v,x_1,x_2,\\colorbox{#e6a23c}{$ (x_2) $},\\colorbox{#e6a23c}{$ (x_4) $},\\colorbox{#e6a23c}{$ ...,u $},\\colorbox{#e6a23c}{$ (x_1) $} $} \\

如果我们取出的区间为：

\v,x_1,x_2,\\colorbox{#e6a23c}{$ (x_2) $},\\colorbox{#e6a23c}{$ (x_4) $},\\colorbox{#e6a23c}{$ ...,u $} \\

就会出错，因为包含了 \((x_2),(x_4)\) 这两个无关的子仙人掌对应的区间，以及 \(x_1,x_2\) 不一定就是我们需要修改的点，如果我们需要修改长链，就需要修改 \(x_4\)，而它却没有出现在我们取出的区间上。

我们可以特殊处理。对于 \(...,u\)，这是链顶为方点的情况，正常处理即可。剩下就是在 \(w\) 对应的环上，修改 \(v\sim x_3\) 的长链 / 短链，这和 LCA 处的问题形式相同。接下来，我们就可以在 \(x_3\) 继续往上跳重链。

如果 \(u\) 为方点呢？注意到，我们上述过程实际保证了 \(u\) 时刻为圆点，就不需要考虑 \(u\) 为方点的情况了。

我们已经可以「修改一对具有祖孙关系 \(v,u\) 间的长 / 短链」。在修改过的 DFS 序上，考虑能不能支持 LCA 处的操作，即修改环上一段连续的链。

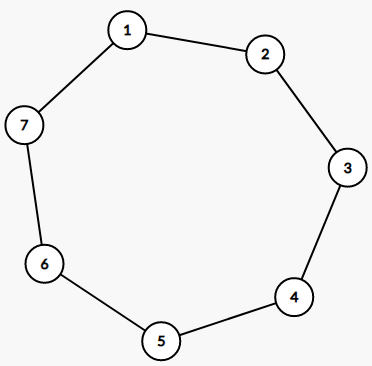
以上图为例，我们假设这个点双对应的方点为 \(u\)，\(u\) 的父亲圆点为 \(1\)，重儿子为 \(5\)。按照我们上面的定义，\(2,3,4\) 在 \(5\) 到 \(1\) 的最长路上，是一类轻儿子，\(6,7\) 则是另一类轻儿子。这个环对应 DFS 序可以为 \(1,{\color{red}7},{\color{yellow}2},{\color{yellow}4},{\color{red}6},{\color{yellow}3},5\)，也可以为 \(1,{\color{red}7},{\color{red}6},{\color{yellow}2},{\color{yellow}3},{\color{yellow}4},5\) 或者 \(1,{\color{yellow}4},{\color{yellow}3},{\color{yellow}2},{\color{red}6},{\color{red}7},5\)，上述三种 DFS 序都是符合目前我们要求的，但是为了解决 LCA 处的问题，我们需要环上连续一段链在 DFS 序上被拆分为 \(\mathcal{O}(1)\) 个区间，也就希望 DFS 序为后两者，或类似后两者的形态。很容易在类似后两种 DFS 序的形态中，拆出我们想要的区间。例如考虑 DFS 为 \(1,{\color{red}7},{\color{red}6},{\color{yellow}2},{\color{yellow}3},{\color{yellow}4},5\)，那么 \(3\rightarrow7\) 的长链为 \(3,4,5,6,7\)，对应 DFS 序区间是 \(5,6\cup7,7\cup2,3\)。

剩下只有子仙人掌操作没有解决了，但是我们惊讶地发现，在修改后的 DFS 序上，在一定程度上很好地保留了 DFS 序一段区间对应子树这个性质，而子仙人掌就是圆方树的子树。具体来说，我们发现 \(u\) 的子仙人掌被拆分成了两部分，一部分是 \(u\) 本身这个点，另一部分为它的不包括本身的子仙人掌。那么只需要分别查询这两段区间的信息就行了。

对于代码实现上的细节，请参考例题代码。时间复杂度瓶颈在于线段树。
例七、【清华集训2015】静态仙人掌（UOJ） Problem Statement

一棵 \(n\) 个点、\(m\) 条边的仙人掌，指定 \(1\) 为根。每个结点有一个颜色（黑或白），初始时均为黑色。有 \(q\) 次操作：

1. 将 \(u\) 到根的最短路径 / 最长路径上所有点的颜色取反。
2. 询问点 \(u\) 子仙人掌中的黑点数目。

\(n,q\leq 5\times10^4\)。
Problem Analysis

问题严格弱于前文的分析的模型，可以用线段树方便维护。可以参考示例代码的具体实现。

时间复杂度：\(\mathcal{O}((n+q)\log n)\)。
Solution

#include <cstdio>
#include <iostream>
#include <vector>
using namespace std;

const int N = 5e4 + 10;
const int M = 1e5 + 10;
const int N2 = N << 1;

int n, m, q;

template <size_t _N, size_t _M>
class Graph {
public:
    Graph(): tot(1) {}
    struct node {
        int v, nxt;
    } edge[_M];
    int head[_N], tot;
    void add(int u, int v) {
        edge[++tot] = { v, head[u] };
        head[u] = tot;
    }
};

Graph<N, M << 1> G;
Graph<N2, N2> T;

int dcc_cnt;

namespace $build {

int dfn[N], low[N], timer;
int stack[N], top;

void tarjan(int u, int fr) {
    dfn[u] = low[u] = ++timer;
    stack[++top] = u;
    for (int i = G.head[u]; i; i = G.edge[i].nxt) {
        if (i == (fr ^ 1)) continue;
        int v = G.edge[i].v;
        if (!dfn[v]) {
            tarjan(v, i);
            low[u] = min(low[u], low[v]);
            if (low[v] >= dfn[u]) {
                ++dcc_cnt;
                T.add(u, dcc_cnt + n);
                while (true) {
                    int x = stack[top--];
                    T.add(dcc_cnt + n, x);
                    if (x == v) break;
                }
            }
        } else {
            low[u] = min(low[u], dfn[v]);
        }
    }
}

}

int siz[N2], son[N2];
int fa[N2], top[N2];
int dfn[N], idx[N], L[N2], R[N2], timer;
int dis[N2], typ[N];
/*
dfn：修改后的 DFS 序
对于圆点：
    idx[u]：在 DFS 序上位置
    L[u]~R[u]：子树（不包括本身）在 DFS 序上的一段区间，或 L[u]=R[u]+1 为空
    dis[u]：环上到环首距离
    typ[u]：类型，0 为重儿子，1 为
对于方点：
    L[u]~R[u]：孩子（轻儿子和重儿子）在 DFS 序上的一段区间
    dis[u]：总环长
*/

void dfs(int u) {
    siz[u] = 1;
    for (int i = T.head[u]; i; i = T.edge[i].nxt) {
        int v = T.edge[i].v;
        fa[v] = u;
        dfs(v), siz[u] += siz[v];
        if (siz[v] > siz[son[u]])
            son[u] = v;
    }
}

void redfs(int u, int tp) {
    top[u] = tp;
    if (u <= n) {
        L[u] = timer + 1;
        if (son[u]) redfs(son[u], tp);
        for (int i = T.head[u]; i; i = T.edge[i].nxt) {
            int v = T.edge[i].v;
            if (v == son[u]) continue;
            redfs(v, v);
        }
        R[u] = timer;
    } else {
        for (int i = T.head[u]; i; i = T.edge[i].nxt) {
            int v = T.edge[i].v;
            dis[v] = ++dis[u];
        }
        ++dis[u];
        L[u] = timer + 1;
        int t = dis[son[u]] <= dis[u] / 2 ? 1 : 2;
        for (int i = T.head[u]; i; i = T.edge[i].nxt) {
            int v = T.edge[i].v;
            if (v == son[u]) t ^= 3;
            else {
                dfn[idx[v] = ++timer] = v;
                typ[v] = t;
            }
        }
        R[u] = timer;
        dfn[idx[son[u]] = ++timer] = son[u];
        typ[son[u]] = 0;
        redfs(son[u], tp);
        for (int i = T.head[u]; i; i = T.edge[i].nxt) {
            int v = T.edge[i].v;
            if (v == son[u]) continue;
            redfs(v, v);
        }
    }
}

namespace $tree {

#define lson (idx << 1)
#define rson (idx << 1 | 1)

struct node {
    int tot[3], val[3];
    bool lazy[3];
} tr[N2 << 2];

void build(int idx, int l, int r) {
    if (l == r) {
        int u = dfn[l];
        if (u <= n) {
            int t = typ[u];
            tr[idx].tot[t] = tr[idx].val[t] = 1;
        }
        return;
    }
    int mid = (l + r) >> 1;
    build(lson, l, mid);
    build(rson, mid + 1, r);
    for (int i = 0; i < 3; ++i) {
        tr[idx].tot[i] = tr[lson].tot[i] + tr[rson].tot[i];
        tr[idx].val[i] = tr[lson].val[i] + tr[rson].val[i];
    }
}

inline void pushtag(int idx, int o) {
    tr[idx].lazy[o] ^= 1;
    tr[idx].val[o] = tr[idx].tot[o] - tr[idx].val[o];
}

inline void pushdown(int idx) {
    for (int o = 0; o < 3; ++o) {
        if (!tr[idx].lazy[o]) continue;
        pushtag(lson, o);
        pushtag(rson, o);
        tr[idx].lazy[o] = 0;
    }
}

void modify(int idx, int trl, int trr, int l, int r, int o) {
    if (l > r) throw;
    if (l <= trl && trr <= r) {
        if (o == 0) {
            for (int i = 0; i < 3; ++i) pushtag(idx, i);
        } else
            pushtag(idx, o), pushtag(idx, 0);
        return;
    }
    pushdown(idx);
    int mid = (trl + trr) >> 1;
    if (l <= mid) modify(lson, trl, mid, l, r, o);
    if (r >  mid) modify(rson, mid + 1, trr, l, r, o);
    for (int i = 0; i < 3; ++i)
        tr[idx].val[i] = tr[lson].val[i] + tr[rson].val[i];
}

int query(int idx, int trl, int trr, int l, int r) {
    if (l > r) throw;
    if (l <= trl && trr <= r)
        return tr[idx].val[0] + tr[idx].val[1] + tr[idx].val[2];
    pushdown(idx);
    int mid = (trl + trr) >> 1;
    if (r <= mid) return query(lson, trl, mid, l, r);
    if (l >  mid) return query(rson, mid + 1, trr, l, r);
    return query(lson, trl, mid, l, r) + query(rson, mid + 1, trr, l, r);
}

#undef lson
#undef rson

}

void modify(int u, int op) {
    // 在跳重链的时候，需要时刻保持 u 为圆点，这是为了简化讨论
    while (top[u] != 1) {
        int v = top[u];
        if (v > n) {
            $tree::modify(1, 1, n, L[v], idx[u], op);
            u = fa[v];
        } else {
            if (u != v)
                $tree::modify(1, 1, n, L[son[v]], idx[u], op);
            u = fa[v];
            int o = dis[v] <= dis[u] / 2 ? 1 : 2;
            if (o == op) {
                $tree::modify(1, 1, n, L[u], idx[v], 0);
                if (dis[son[u]] <= dis[v])
                    $tree::modify(1, 1, n, idx[son[u]], idx[son[u]], 0);
            } else {
                $tree::modify(1, 1, n, idx[v], R[u], 0);
                if (dis[son[u]] >= dis[v])
                    $tree::modify(1, 1, n, idx[son[u]], idx[son[u]], 0);
            }
            u = fa[u];
        }
    }
    $tree::modify(1, 1, n, idx[1], idx[u], op);
}

int query(int u) {
    int res = 0;
    res += $tree::query(1, 1, n, idx[u], idx[u]);
    if (L[u] <= R[u])
        res += $tree::query(1, 1, n, L[u], R[u]);
    return res;
}

int main() {
    scanf("%d%d%d", &n, &m, &q);
    for (int i = 1, u, v; i <= m; ++i) {
        scanf("%d%d", &u, &v);
        G.add(u, v), G.add(v, u);
    }
    $build::tarjan(1, 0);
    dfs(1);
    dfn[idx[1] = ++timer] = 1;
    redfs(1, 1);
    $tree::build(1, 1, n);
    for (int op, u; q--; ) {
        scanf("%d%d", &op, &u);
        if (op <= 2) modify(u, op);
        else printf("%d\n", query(u));
    }
    return 0;
}

类型四：静态仙人掌，求给定点集的整体信息

这类问题每次询问会给出一个点集，求这个点集的整体信息，比如统计一些东西，做一些 DP 什么的，类似于类型一，只不过只关于点集中的点了。

对于树上给定点集的问题，我们可以建出这些点的虚树，在虚树上统计答案，做树形 DP。由于点集 \(S\) 对应虚树结点个数是 \(\mathcal{O}(|S|)\) 的，时间复杂度得到了保证。

唯一需要注意的是，对于方点 \(u\)，其虚树上一个孩子 \(v\)，那么不能想当然地认为 \(v\) 是 \(u\) 的孩子圆点，事实上，\(v\) 并不一定是其孩子圆点，甚至连个圆点都可能不是。所以，我们需要通过一些方法求出 \(v'\)，这个才是 \(u\) 的孩子圆点。
例八、mx 的仙人掌（UOJ） Problem Statement

一棵 \(n\) 个点、\(m\) 条边的仙人掌。

\(q\) 此询问，每次给出一个点集 \(S\)。求出从 \(S\) 中选出两个点 \(u,v\)，他们之间最短路的最大值是多少，\(u,v\) 可以相同。

\(n,\sum|S|\leq3\times10^5\)。
Problem Analysis

每次可以 \(\mathcal{O}(n)\) 类似类型一求直径，做一遍圆方树上的树形 DP。

那么先把虚树建出来。然后考虑在 LCA 处统计答案，即枚举 LCA \(p\)，考虑它两个孩子的子树中的点 \(u,v\) 对答案的贡献。分 \(p\) 为方点、圆点讨论。

1. \(p\) 为圆点：
   此时 \(u,v\) 之间的最短路即为 \(s_u+s_v-2s_p\)，其中 \(s_u\) 表示圆方树边权的树上前缀和。我们只需要求出 \(s_u+s_v\) 的最大值。这个很容易，对于每个点 \(u\) 维护 \(f_u\) 表示子树中 \(s_u\) 的最大值，然后就可以统计了。
2. \(p\) 为方点：
   设 \(u',v'\) 表示 \(p\) 在圆方树上两个孩子，对应为 \(u,v\) 的祖先。\(u',v'\) 可以 kth-kather 求出。此时 \(u,v\) 之间的最短路为 \(s_u-s_{u'}+s_v-s_{v'} + \min\{|d_{v'}-d_{u'}|,\operatorname{sum}(p)-|d_{v'}-d_{u'}|\}\)，其中 \(\operatorname{sum}(p)\) 表示方点 \(p\) 对应的环的总长，\(d_u\) 表示 \(u\) 到环首的距离。相当于 \(p\) 的每个孩子 \(u\) 有一个点权 \(w_u=f_u-s_u\)，要求 \(\max\limits_{u,v\in\operatorname{son}(p)}\Bigg\{w_u+w_v + \min\Big\{|d_v-d_u|,\operatorname{sum}(p)-|d_v-d_u|\Big\}\Bigg\}\)，这个可以拆换成链，再复制一份接在后面，然后就能单调队列做了。

时间复杂度为：\(\mathcal{O}(m+n\log n+\sum|S|(\log|S|+\log n))\)。
Solution

#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;

using ll = long long;

const int N = 3e5 + 10;
const int M = N * 3 + 10;
const int NN = N << 1;
const int lg2N = __lg(NN) + 1;

int n, m, q;

template <size_t _N, size_t _M, typename T>
class Grpah {
public:
    Grpah(): tot(1) {}
    struct node {
        int v, nxt;
        T w;
    } edge[_M];
    int head[_N], tot;
    void add(int u, int v, const T& w) {
        edge[++tot] = { v, head[u], w };
        head[u] = tot;
    }
};
Grpah<N, M << 1, int> G;  // original grpah
Grpah<N << 1, N << 1, ll> T;  // rebuild tree

template <size_t _N, size_t _M>
class Graph_ {
public:
    Graph_(): tot(1) {}
    struct node {
        int v, nxt;
    } edge[_M];
    int head[_N], tot;
    void add(int u, int v) {
        edge[++tot] = { v, head[u] };
        head[u] = tot;
    }
};
Graph_<N << 1, N << 1> VT;  // virtual tree

int dcc_cnt;
ll cirsum[N], dis[N];

namespace $build {

int dfn[N], low[N], timer;
int stack[M], top;  // 注意这里的边栈的数组大小

void tarjan(int u, int fr) {
    dfn[u] = low[u] = ++timer;
    for (int i = G.head[u]; i; i = G.edge[i].nxt) {
        if (i == (fr ^ 1)) continue;
        int v = G.edge[i].v;
        if (!dfn[v]) {
            stack[++top] = i;
            tarjan(v, i);
            low[u] = min(low[u], low[v]);
            if (low[v] >= dfn[u]) {
                static int tmp[N];
                int tot = 0;
                ++dcc_cnt;
                while (true) {
                    int j = stack[top--];
                    int uu = G.edge[j ^ 1].v;
                    int vv = G.edge[j].v;
                    int w = G.edge[j].w;
                    cirsum[dcc_cnt] += w;
                    if (j == i) break;
                    dis[uu] = dis[vv] + w;
                    tmp[++tot] = uu;
                }
                if (tot == 0) {
                    tmp[++tot] = v;
                    dis[v] = cirsum[dcc_cnt];
                    cirsum[dcc_cnt] <<= 1;
                }
                T.add(u, dcc_cnt + n, 0);
                for (int j = 1; j <= tot; ++j) {
                    int x = tmp[j];
                    T.add(dcc_cnt + n, x, min(dis[x], cirsum[dcc_cnt] - dis[x]));
                }
            }
        } else {
            low[u] = min(low[u], dfn[v]);
            if (dfn[v] < dfn[u])
                stack[++top] = i;
        }
    }
}

}

int dpt[NN], fa[NN], timer, kthfa[lg2N][NN];
int idx[NN], st[lg2N][NN];
ll sum[NN];  // tree prefix sum

void dfs(int u) {
    st[0][idx[u] = ++timer] = u;
    for (int i = T.head[u]; i; i = T.edge[i].nxt) {
        int v = T.edge[i].v;
        ll w = T.edge[i].w;
        dpt[v] = dpt[u] + 1;
        fa[v] = kthfa[0][v] = u;
        sum[v] = sum[u] + w;
        dfs(v);
    }
}
inline int Min(int a, int b) {
    return dpt[a] < dpt[b] ? a : b;
}
inline int lca(int u, int v) {
    if (u == v) return u;
    if ((u = idx[u]) > (v = idx[v])) swap(u, v);
    int k = __lg(v - u++);
    return fa[Min(st[k][u], st[k][v - (1 << k) + 1])];
}
inline int jump(int u, int k) {
    for (int i = lg2N - 1; ~i; --i)
        if (k & 1 << i) u = kthfa[i][u];
    return u;
}

ll ans, f[NN];
int bl[NN];  // 设 v 为 u 在虚树上的父亲，bl[u] 为 v 的一个在圆方树上的孩子，且为 u 的祖先

void redfs(int u) {
    f[u] = sum[u];
    if (u <= n) {
        for (int i = VT.head[u]; i; i = VT.edge[i].nxt) {
            int v = VT.edge[i].v;
            redfs(v);
            ans = max(ans, f[v] + f[u] - 2 * sum[u]);
            f[u] = max(f[u], f[v]);
        }
    } else {
        for (int i = VT.head[u]; i; i = VT.edge[i].nxt) {
            int v = VT.edge[i].v;
            redfs(v);
            f[u] = max(f[u], f[v]);
        }
        // do algorithm after dfs!
        static int son[N];
        static ll d[NN], w[NN];
        static int Q[NN];
        int cnt = 0;
        for (int i = VT.head[u]; i; i = VT.edge[i].nxt) {
            int v = VT.edge[i].v;
            son[++cnt] = v;
        }
        sort(son + 1, son + cnt + 1, [] (int a, int b) {
            return dis[bl[a]] < dis[bl[b]];
        });
        ll tot = cirsum[u - n];
        for (int i = 1; i <= cnt; ++i) {
            int v = son[i];
            int tv = bl[v];
            d[i] = dis[tv];
            w[i] = f[v] - sum[tv];
            d[cnt + i] = d[i] + tot;
            w[cnt + i] = w[i];
        }
        int head = 0, tail = -1;
        for (int i = 1; i <= cnt << 1; ++i) {
            while (head <= tail && d[Q[head]] < d[i] - tot/2) ++head;
            if (head <= tail) ans = max(ans, w[Q[head]] + w[i] + d[i] - d[Q[head]]);
            while (head <= tail && w[Q[tail]] - d[Q[tail]] <= w[i] - d[i]) --tail;
            Q[++tail] = i;
        }
        
        // for (int i = 1; i <= cnt; ++i)
        //     for (int j = i + 1; j <= cnt; ++j) {
        //         ll D = abs(d[i] - d[j]);
        //         ans = max(ans, w[i] + w[j] + min(D, tot - D));
        //     }
    }
}

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1, u, v, w; i <= m; ++i) {
        scanf("%d%d%d", &u, &v, &w);
        G.add(u, v, w);
        G.add(v, u, w);
    }
    $build::tarjan(1, 0);
    dfs(1);
    for (int k = 1; k < lg2N; ++k) {
        for (int i = 1; i + (1 << k) - 1 <= n + dcc_cnt; ++i)
            st[k][i] = Min(st[k - 1][i], st[k - 1][i + (1 << (k - 1))]);
        for (int i = 1; i <= n + dcc_cnt; ++i)
            kthfa[k][i] = kthfa[k - 1][kthfa[k - 1][i]];
    }
    scanf("%d", &q);
    for (int k; q--; ) {
        static int st[NN];
        scanf("%d", &k);
        for (int i = 1; i <= k; ++i)
            scanf("%d", &st[i]);
        sort(st + 1, st + k + 1, [] (int a, int b) {
            return idx[a] < idx[b];
        });
        for (int i = 1; i < k; ++i)
            st[k + i] = lca(st[i], st[i + 1]);
        sort(st + 1, st + k * 2, [] (int a, int b) {
            return idx[a] < idx[b];
        });
        int m = unique(st + 1, st + k * 2) - st - 1;
        for (int i = 1; i < m; ++i) {
            int u = st[i + 1], v = lca(st[i], st[i + 1]);
            VT.add(v, u);
            if (v > n) {
                int _u = jump(u, dpt[u] - dpt[v] - 1);
                bl[u] = _u;
            }
        }
        ans = 0;
        redfs(st[1]);
        printf("%lld\n", ans);
        VT.tot = 1;
        for (int i = 1; i <= m; ++i) {
            int u = st[i];
            VT.head[u] = 0;
        }
    }
    return 0;
}

使用 $\\mathcal{O}(1)$ 查找 $u',v'$ 算法(https://www.cnblogs.com/XuYueming/p/18919143)

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <tuple>
using namespace std;

using ll = long long;

const int N = 3e5 + 10;
const int M = N * 3 + 10;
const int NN = N << 1;
const int lg2N = __lg(NN) + 1;

int n, m, q;

template <size_t _N, size_t _M, typename T>
class Grpah {
public:
    Grpah(): tot(1) {}
    struct node {
        int v, nxt;
        T w;
    } edge[_M];
    int head[_N], tot;
    void add(int u, int v, const T& w) {
        edge[++tot] = { v, head[u], w };
        head[u] = tot;
    }
};
Grpah<N, M << 1, int> G;  // original grpah
Grpah<N << 1, N << 1, ll> T;  // rebuild tree

template <size_t _N, size_t _M>
class Graph_ {
public:
    Graph_(): tot(1) {}
    struct node {
        int v, nxt;
    } edge[_M];
    int head[_N], tot;
    void add(int u, int v) {
        edge[++tot] = { v, head[u] };
        head[u] = tot;
    }
};
Graph_<N << 1, N << 1> VT;  // virtual tree

int dcc_cnt;
ll cirsum[N], dis[N];

namespace $build {

int dfn[N], low[N], timer;
int stack[M], top;  // 注意这里的边栈的数组大小

void tarjan(int u, int fr) {
    dfn[u] = low[u] = ++timer;
    for (int i = G.head[u]; i; i = G.edge[i].nxt) {
        if (i == (fr ^ 1)) continue;
        int v = G.edge[i].v;
        if (!dfn[v]) {
            stack[++top] = i;
            tarjan(v, i);
            low[u] = min(low[u], low[v]);
            if (low[v] >= dfn[u]) {
                static int tmp[N];
                int tot = 0;
                ++dcc_cnt;
                while (true) {
                    int j = stack[top--];
                    int uu = G.edge[j ^ 1].v;
                    int vv = G.edge[j].v;
                    int w = G.edge[j].w;
                    cirsum[dcc_cnt] += w;
                    if (j == i) break;
                    dis[uu] = dis[vv] + w;
                    tmp[++tot] = uu;
                }
                if (tot == 0) {
                    tmp[++tot] = v;
                    dis[v] = cirsum[dcc_cnt];
                    cirsum[dcc_cnt] <<= 1;
                }
                T.add(u, dcc_cnt + n, 0);
                for (int j = 1; j <= tot; ++j) {
                    int x = tmp[j];
                    T.add(dcc_cnt + n, x, min(dis[x], cirsum[dcc_cnt] - dis[x]));
                }
            }
        } else {
            low[u] = min(low[u], dfn[v]);
            if (dfn[v] < dfn[u])
                stack[++top] = i;
        }
    }
}

}

int dpt[NN], fa[NN], timer;
int idx[NN], st[lg2N][NN];
ll sum[NN];  // tree prefix sum

void dfs(int u) {
    st[0][idx[u] = ++timer] = u;
    for (int i = T.head[u]; i; i = T.edge[i].nxt) {
        int v = T.edge[i].v;
        ll w = T.edge[i].w;
        dpt[v] = dpt[u] + 1;
        fa[v] = u;
        sum[v] = sum[u] + w;
        dfs(v);
    }
}
inline int Min(int a, int b) {
    return dpt[a] < dpt[b] ? a : b;
}
inline tuple<int, int, int> lca(int u, int v) {
    if (u == v) return { 0, 0, u };
    int U, V, p, iu = idx[u], iv = idx[v];
    bool F = false;
    if (iu > iv) swap(iu, iv), swap(u, v), F = true;
    int k = __lg(iv - iu);
    V = Min(st[k][iu + 1], st[k][iv - (1 << k) + 1]);
    p = fa[V];
    if (p == u) U = 0;
    else {
        int ip = idx[p];
        k = __lg(iu - ip++);
        U = Min(st[k][ip], st[k][iu - (1 << k) + 1]);
    }
    if (F) swap(U, V);
    return { U, V, p };
}

ll ans, f[NN];
int bl[NN];  // 设 v 为 u 在虚树上的父亲，bl[u] 为 v 的一个在圆方树上的孩子，且为 u 的祖先

void redfs(int u) {
    f[u] = sum[u];
    if (u <= n) {
        for (int i = VT.head[u]; i; i = VT.edge[i].nxt) {
            int v = VT.edge[i].v;
            redfs(v);
            ans = max(ans, f[v] + f[u] - 2 * sum[u]);
            f[u] = max(f[u], f[v]);
        }
    } else {
        for (int i = VT.head[u]; i; i = VT.edge[i].nxt) {
            int v = VT.edge[i].v;
            redfs(v);
            f[u] = max(f[u], f[v]);
        }
        // do algorithm after dfs!
        static int son[N];
        static ll d[NN], w[NN];
        static int Q[NN];
        int cnt = 0;
        for (int i = VT.head[u]; i; i = VT.edge[i].nxt) {
            int v = VT.edge[i].v;
            son[++cnt] = v;
        }
        sort(son + 1, son + cnt + 1, [] (int a, int b) {
            return dis[bl[a]] < dis[bl[b]];
        });
        ll tot = cirsum[u - n];
        for (int i = 1; i <= cnt; ++i) {
            int v = son[i];
            int tv = bl[v];
            d[i] = dis[tv];
            w[i] = f[v] - sum[tv];
            d[cnt + i] = d[i] + tot;
            w[cnt + i] = w[i];
        }
        int head = 0, tail = -1;
        for (int i = 1; i <= cnt << 1; ++i) {
            while (head <= tail && d[Q[head]] < d[i] - tot/2) ++head;
            if (head <= tail) ans = max(ans, w[Q[head]] + w[i] + d[i] - d[Q[head]]);
            while (head <= tail && w[Q[tail]] - d[Q[tail]] <= w[i] - d[i]) --tail;
            Q[++tail] = i;
        }
        
        // for (int i = 1; i <= cnt; ++i)
        //     for (int j = i + 1; j <= cnt; ++j) {
        //         ll D = abs(d[i] - d[j]);
        //         ans = max(ans, w[i] + w[j] + min(D, tot - D));
        //     }
    }
}

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1, u, v, w; i <= m; ++i) {
        scanf("%d%d%d", &u, &v, &w);
        G.add(u, v, w);
        G.add(v, u, w);
    }
    $build::tarjan(1, 0);
    dfs(1);
    for (int k = 1; k < lg2N; ++k) {
        for (int i = 1; i + (1 << k) - 1 <= n + dcc_cnt; ++i)
            st[k][i] = Min(st[k - 1][i], st[k - 1][i + (1 << (k - 1))]);
    }
    scanf("%d", &q);
    for (int k; q--; ) {
        static int st[NN];
        scanf("%d", &k);
        for (int i = 1; i <= k; ++i)
            scanf("%d", &st[i]);
        sort(st + 1, st + k + 1, [] (int a, int b) {
            return idx[a] < idx[b];
        });
        for (int i = 1; i < k; ++i)
            st[k + i] = get<2>(lca(st[i], st[i + 1]));
        sort(st + 1, st + k * 2, [] (int a, int b) {
            return idx[a] < idx[b];
        });
        int m = unique(st + 1, st + k * 2) - st - 1;
        for (int i = 1; i < m; ++i) {
            int u = st[i + 1];
            auto [_, U, v] = lca(st[i], st[i + 1]);
            VT.add(v, u);
            if (v > n) bl[u] = U;
        }
        ans = 0;
        redfs(st[1]);
        printf("%lld\n", ans);
        VT.tot = 1;
        for (int i = 1; i <= m; ++i) {
            int u = st[i];
            VT.head[u] = 0;
        }
    }
    return 0;
}

例九、【集训队互测2016】火车司机出秦川（UOJ） Problem Statement

一棵 \(n\) 个点、\(m\) 条边的仙人掌，有边权，和 \(2q\) 次操作。

询问，第 \(i\) 次询问有 \(k_i\) 条简单路径，称作「路径」。一条「路径」用三个整数 \((u,v,0/1)\) 表示，其中 \(u,v\) 表示它的端点，\(0\) 表示「路径」为 \(u,v\) 之间所有简单路径中经过最少结点的那条，\(1\) 表示经过最多结点的那条。保证「路径」端点不重复，保证所有环为奇环。求这些「路径」的并的边权和。

每次询问后可能跟着一条边权的修改。

\(n,\sum|k_i|\leq3\times10^5\)。
Problem Analysis

先把这些「路径」的端点在圆方树上的虚树建出来。下称经过最少城市的路径称作最短路，与边权最短路区别，同理最长路。

考虑哪些东西会对答案产生贡献，也就是考虑一条「路径」可能会包含哪些边。LCA \(p\) 若是圆点，就包含了 \(p\rightarrow u\) 和 \(p\rightarrow v\) 的最长 / 最短路。\(p\) 若是方点，就包含了 \(u'\rightarrow u\)，\(v'\rightarrow v\) 的最长 / 最短路，这个和前面的问题形式是相同的，以及 \(p\) 对应环上 \(u'\rightarrow v'\) 的最长 / 最短路。

先不考虑修改，如果只有第一种问题怎么求。一条虚树边对应圆方树上一条方圆交错的路径，在原仙人掌上体现为，若干个简单环被连接成一个链状的结构。差分之后做树上前缀和，就能知道一条虚树边是否需要统计最短 / 最长路。而知道了是否需要统计最短 / 最长路，我们也很方便求出这一条链的贡献了。记 \(s_{0/1}(u)\) 表示 \(u\) 到根的最短 / 最长路路径长度，好像这样可以计算了，对于只需要统计最短 / 最长路，就是 \(s_{0/1}\) 相减，对于两个都需要统计，就是 \(s_0(u)+s_1(u)\) 相减......吗？对于环来说，最短最长路加在一起正好凑成了一个整个环，但是对于一条非环边来说就被重复统计了。所以此时对于「两点被一边相连」这种点双不能再当做一个环考虑了。还需要维护 \(s_2(u)\) 表示 \(u\) 到根的非环边路径长度。两种路径都要统计时，就是 \(s_0(u)+s_1(u)-s_2(u)\) 相减。

考虑如果只有第二种问题怎么求。不妨令在环的顺序下 \(u'\) 在 \(v'\) 之前，那么最短 / 最长路，就是 \(u'\sim v', v'\sim tail\sim head\sim u'\) 这两条路径中较短 / 长的那条。可以用差分完成区间覆盖，然后也能统计了。

如果两种问题同时存在，需要注意，第一种问题的路径可能会经过第二种路径的环，这个在第二个问题里面特殊处理一下，看看需不需要额外添加一些覆盖区间。

如果有了修改呢？如果这是一条环边，会影响到：总环长，这个很好维护；增加环上后缀所有点的到环首距离，所以需要对每个环开一个树状数组；对连续一段子树的 \(s_{0/1}\) 造成影响，这个用树状数组维护 DFS 序，就是区间加。如果这是一条非环边，会对子树的 \(s_{0/1/2}\) 产生增量，这个也用树状数组维护。

时间复杂度：\(\mathcal{O}(m+(n+q+\sum|S|)\log n)\)。
Solution

给出了没有修改的部分分代码，方便理解。
没有修改

#include <cstdio>
#include <iostream>
#include <set>
#include <algorithm>
#include <vector>
using namespace std;

using ll = long long;

const int N = 3e5 + 10;
const int M = N * 2 + 10;
const int NN = N << 1;
const int lg2N = __lg(NN) + 1;

int n, m, q;

template <size_t _N, size_t _M, typename T>
class Grpah {
public:
    Grpah(): tot(1) {}
    struct node {
        int v, nxt;
        T w;
    } edge[_M];
    int head[_N], tot;
    void add(int u, int v, const T& w) {
        edge[++tot] = { v, head[u], w };
        head[u] = tot;
    }
};
Grpah<N, M << 1, int> G;  // original grpah
Grpah<N << 1, N << 1, ll> T;  // rebuild tree

template <size_t _N, size_t _M>
class Graph_ {
public:
    Graph_(): tot(1) {}
    struct node {
        int v, nxt;
    } edge[_M];
    int head[_N], tot;
    void add(int u, int v) {
        edge[++tot] = { v, head[u] };
        head[u] = tot;
    }
};
Graph_<N << 1, N << 1> VT;  // virtual tree

int dcc_cnt;
ll cirSum[N], dis[N];
int cirTot[N], cirDpt[N];

bool notInCir[M];
ll s[3][NN];  // tree prefix sum

namespace $build {

int dfn[N], low[N], timer;
int stack[M], top;

void tarjan(int u, int fr) {
    dfn[u] = low[u] = ++timer;
    for (int i = G.head[u]; i; i = G.edge[i].nxt) {
        if (i == (fr ^ 1)) continue;
        int v = G.edge[i].v;
        if (!dfn[v]) {
            stack[++top] = i;
            tarjan(v, i);
            low[u] = min(low[u], low[v]);
            if (low[v] >= dfn[u]) {
                static int tmp[N];
                int tot = 0;
                ++dcc_cnt;
                while (true) {
                    int j = stack[top--];
                    int uu = G.edge[j ^ 1].v;
                    int vv = G.edge[j].v;
                    int w = G.edge[j].w;
                    cirSum[dcc_cnt] += w;
                    if (j == i) break;
                    dis[uu] = dis[vv] + w;
                    cirDpt[uu] = cirDpt[vv] + 1;
                    tmp[++tot] = uu;
                }
                cirTot[dcc_cnt] = tot + 1;
                if (tot == 0) {
                    T.add(u, dcc_cnt + n, 0);
                    T.add(dcc_cnt + n, v, -cirSum[dcc_cnt]);  // 负数表示非环边
                    notInCir[i >> 1] = true;
                } else {
                    T.add(u, dcc_cnt + n, 0);
                    for (int j = 1; j <= tot; ++j) {
                        int x = tmp[j];
                        ll len;
                        if (cirDpt[x] < cirTot[dcc_cnt] - cirDpt[x])
                            len = dis[x];
                        else
                            len = cirSum[dcc_cnt] - dis[x];
                        T.add(dcc_cnt + n, x, len);
                    }
                }
            }
        } else {
            low[u] = min(low[u], dfn[v]);
            if (dfn[v] < dfn[u])
                stack[++top] = i;
        }
    }
}

}

int dpt[NN], fa[NN], timer, kthfa[lg2N][NN];
int idx[NN], st[lg2N][NN];

void dfs(int u) {
    st[0][idx[u] = ++timer] = u;
    for (int i = T.head[u]; i; i = T.edge[i].nxt) {
        int v = T.edge[i].v;
        ll w = T.edge[i].w;
        dpt[v] = dpt[u] + 1;
        fa[v] = kthfa[0][v] = u;
        
        if (u <= n) {
            s[0][v] = s[0][u];
            s[1][v] = s[1][u];
            s[2][v] = s[2][u];
        } else if (w > 0) {
            s[2][v] = s[2][u];
            s[0][v] = s[0][u] + w;
            s[1][v] = s[1][u] + (cirSum[u - n] - w);
        } else {
            w = -w;
            s[2][v] = s[2][u] + w;
            s[0][v] = s[0][u] + w;
            s[1][v] = s[1][u] + w;
        }
        
        dfs(v);
    }
}
inline int Min(int a, int b) {
    return dpt[a] < dpt[b] ? a : b;
}
inline int lca(int u, int v) {
    if (u == v) return u;
    if ((u = idx[u]) > (v = idx[v])) swap(u, v);
    int k = __lg(v - u++);
    return fa[Min(st[k][u], st[k][v - (1 << k) + 1])];
}
inline int jump(int u, int k) {
    for (int i = lg2N - 1; ~i; --i)
        if (k & 1 << i) u = kthfa[i][u];
    return u;
}

struct {
    int u, v, tp;
    int _u, _v;
} rd[N];  // Road

int bl[NN];  // 设 v 为 u 在虚树上的父亲，bl[u] 为 v 的一个在圆方树上的孩子，且为 u 的祖先
int cha[2][NN], _cha[2][NN];
vector<int> vec[NN];  // 方点 LCA 处的特殊处理
long long qans;

void redfs(int u) {
    if (u <= n) {
        for (int i = VT.head[u]; i; i = VT.edge[i].nxt) {
            int v = VT.edge[i].v;
            redfs(v);
            int w0 = cha[0][v], w1 = cha[1][v];
            cha[0][u] += w0;
            cha[1][u] += w1;
            long long x0 = s[0][v] - s[0][u];
            long long x1 = s[1][v] - s[1][u];
            long long x2 = s[2][v] - s[2][u];
            if (w0 && w1) {
                qans += x0 + x1 - x2;
            } else if (w0) {
                qans += x0;
            } else if (w1) {
                qans += x1;
            }
        }
    } else {
        for (int i = VT.head[u]; i; i = VT.edge[i].nxt) {
            int v = VT.edge[i].v;
            redfs(v);
            int w0 = cha[0][v], w1 = cha[1][v];
            long long x0 = s[0][v] - s[0][bl[v]];
            long long x1 = s[1][v] - s[1][bl[v]];
            long long x2 = s[2][v] - s[2][bl[v]];
            if (w0 && w1) {
                qans += x0 + x1 - x2;
            } else if (w0) {
                qans += x0;
            } else if (w1) {
                qans += x1;
            }
        }
        vector<pair<ll, int>> tmp;
        for (int id : vec[u]) {
            int uu = rd[id]._u;
            int vv = rd[id]._v;
            int tp = rd[id].tp;
            if (cirDpt[uu] > cirDpt[vv])
                swap(uu, vv);
            int A = cirDpt[vv] - cirDpt[uu];  // uu -> vv
            int B = cirTot[u - n] - A;  // uu -> head -> tail -> vv
            if (tp == (A > B)) {
                // A
                tmp.emplace_back(dis[uu], 1);
                tmp.emplace_back(dis[vv], -1);
            } else {
                // B
                tmp.emplace_back(0, 1);
                tmp.emplace_back(dis[uu], -1);
                tmp.emplace_back(dis[vv], 1);
            }
        }
        for (int i = VT.head[u]; i; i = VT.edge[i].nxt) {
            int v = VT.edge[i].v;
            int vv = bl[v];
            int w0 = cha[0][v], w1 = cha[1][v];
            w0 += _cha[0][vv], w1 += _cha[1][vv];
            cha[0][u] += w0;
            cha[1][u] += w1;
            int L = cirDpt[vv];
            int R = cirTot[u - n] - L;
            if (w0 && w1) {
                tmp.emplace_back(0, 1);
            } else if (w0 || w1) {
                if (bool(w0) == (L < R)) {
                    tmp.emplace_back(0, 1);
                    tmp.emplace_back(dis[vv], -1);
                } else {
                    tmp.emplace_back(dis[vv], 1);
                }
            }
        }
        sort(tmp.begin(), tmp.end());
        int m = tmp.size();
        int sum = 0;
        for (int i = 0, j = -1; i < m; i = j + 1) {
            while (j + 1 < m && tmp[j + 1].first == tmp[i].first)
                sum += tmp[++j].second;
            ll len;
            if (j == m - 1)
                len = cirSum[u - n] - tmp[i].first;
            else
                len = tmp[j + 1].first - tmp[i].first;
            if (sum) {
                qans += len;
            }
        }
    }
}

void query() {
    static int st[NN], _st[NN];
    int k;
    scanf("%d", &k);
    if (!k) {
        puts("0");
        return;
    }
    int m = 0;
    for (int i = 1; i <= k; ++i) {
        scanf("%d%d%d", &rd[i].u, &rd[i].v, &rd[i].tp);
        st[++m] = rd[i].u;
        st[++m] = rd[i].v;
    }
    sort(st + 1, st + m + 1, [] (int a, int b) {
        return idx[a] < idx[b];
    });
    for (int i = 1; i < m; ++i)
        st[m + i] = lca(st[i], st[i + 1]);
    sort(st + 1, st + m * 2, [] (int a, int b) {
        return idx[a] < idx[b];
    });
    m = unique(st + 1, st + m * 2) - st - 1;
    int _m = 0;
    for (int i = 1; i < m; ++i) {
        int u = st[i + 1], v = lca(st[i], st[i + 1]);
        VT.add(v, u);
        if (v > n) {
            int _u = jump(u, dpt[u] - dpt[v] - 1);
            _st[++_m] = _u;
            bl[u] = _u;
        }
    }
    for (int i = 1; i <= k; ++i) {
        int u = rd[i].u, v = rd[i].v, w = rd[i].tp;
        int p = lca(u, v);
        if (p > n) {
            int _u = jump(u, dpt[u] - dpt[p] - 1);
            int _v = jump(v, dpt[v] - dpt[p] - 1);
            ++cha[w][u], --_cha[w][_u];
            ++cha[w][v], --_cha[w][_v];
            rd[i]._u = _u;
            rd[i]._v = _v;
            vec[p].emplace_back(i);
        } else {
            ++cha[w][u], ++cha[w][v];
            cha[w][p] -= 2;
        }
    }
    qans = 0;
    redfs(st[1]);
    printf("%lld\n", qans);
    VT.tot = 1;
    for (int i = 1; i <= m; ++i) {
        int u = st[i];
        VT.head[u] = 0;
        vec[u].clear();
        cha[0][u] = cha[1][u] = 0;
    }
    for (int i = 1; i <= _m; ++i) {
        int u = _st[i];
        _cha[0][u] = _cha[1][u] = 0;
    }
}

void modify() {
    int w, x;
    scanf("%d%d", &w, &x);
    if (!w) return;
    throw;
}

int main() {
    scanf("%d%d%d", &n, &m, &q);
    for (int i = 1, u, v, w; i <= m; ++i) {
        scanf("%d%d%d", &u, &v, &w);
        G.add(u, v, w);
        G.add(v, u, w);
    }
    $build::tarjan(1, 0);
    dfs(1);
    for (int k = 1; k < lg2N; ++k) {
        for (int i = 1; i + (1 << k) - 1 <= n + dcc_cnt; ++i)
            st[k][i] = Min(st[k - 1][i], st[k - 1][i + (1 << (k - 1))]);
        for (int i = 1; i <= n + dcc_cnt; ++i)
            kthfa[k][i] = kthfa[k - 1][kthfa[k - 1][i]];
    }
    while (q--) query(), modify();
    return 0;
}

满分做法

#include <cstdio>
#include <iostream>
#include <set>
#include <algorithm>
#include <vector>
#include <cassert>
using namespace std;

using ll = long long;

const int N = 3e5 + 10;
const int M = N * 2 + 10;
const int NN = N << 1;
const int lg2N = __lg(NN) + 1;

int n, m, q;

template <size_t _N, size_t _M, typename T>
class Grpah {
public:
    Grpah(): tot(1) {}
    struct node {
        int v, nxt;
        T w;
    } edge[_M];
    int head[_N], tot;
    void add(int u, int v, const T& w) {
        edge[++tot] = { v, head[u], w };
        head[u] = tot;
    }
};
Grpah<N, M << 1, int> G;  // original grpah
Grpah<N << 1, N << 1, ll> T;  // rebuild tree

template <size_t _N, size_t _M>
class Graph_ {
public:
    Graph_(): tot(1) {}
    struct node {
        int v, nxt;
    } edge[_M];
    int head[_N], tot;
    void add(int u, int v) {
        edge[++tot] = { v, head[u] };
        head[u] = tot;
    }
};
Graph_<N << 1, N << 1> VT;  // virtual tree

template <typename T>
class Bit_Tree {
private:
    vector<T> tree;
    int size() const { return tree.size(); }
    void _modify(int p, T v) {
        for (; p <= size(); p += p & -p)
            tree[p - 1] += v;
    }
    T query(int p) const {
        T res = 0;
        for (; p; p &= p - 1)
            res += tree[p - 1];
        return res;
    }
public:
    void init(int n) {
        tree = vector<T>(n, 0);
    }
    void modify(int l, int r, T v) {
        assert(1 <= l && l <= r && r <= size());
        _modify(l, v);
        _modify(r + 1, -v);
    }
    void modify(int p, T v) {
        assert(1 <= p && p <= size());
        modify(p, p, v);
    }
    T operator [] (int p) const {
        assert(1 <= p && p <= size());
        return query(p);
    }
};

int dcc_cnt;
ll cirSum[N];
Bit_Tree<ll> dis[N];
vector<int> circle[N];
int cirTot[N], cirDpt[N];

bool notInCir[M];

namespace $build {

int dfn[N], low[N], timer;
int stack[M], top;

void tarjan(int u, int fr) {
    dfn[u] = low[u] = ++timer;
    for (int i = G.head[u]; i; i = G.edge[i].nxt) {
        if (i == (fr ^ 1)) continue;
        int v = G.edge[i].v;
        if (!dfn[v]) {
            stack[++top] = i;
            tarjan(v, i);
            low[u] = min(low[u], low[v]);
            if (low[v] >= dfn[u]) {
                static int tmp[N];
                int tot = 0;
                ++dcc_cnt;
                for (int ttop = top; ; ) {
                    int j = stack[ttop--];
                    int uu = G.edge[j ^ 1].v;
                    if (j == i) break;
                    tmp[++tot] = uu;
                    circle[dcc_cnt].emplace_back(uu);
                }
                dis[dcc_cnt].init(tot);
                while (true) {
                    int j = stack[top--];
                    int uu = G.edge[j ^ 1].v;
                    int vv = G.edge[j].v;
                    int w = G.edge[j].w;
                    cirSum[dcc_cnt] += w;
                    if (j == i) break;
                    cirDpt[uu] = cirDpt[vv] + 1;
                    dis[dcc_cnt].modify(cirDpt[uu], tot, w);
                }
                cirTot[dcc_cnt] = tot + 1;
                if (tot == 0) {
                    T.add(u, dcc_cnt + n, 0);
                    T.add(dcc_cnt + n, v, -cirSum[dcc_cnt]);  // 负数表示非环边
                    notInCir[i >> 1] = true;
                } else {
                    T.add(u, dcc_cnt + n, 0);
                    for (int j = tot; j; --j) {  // attention, reversed
                        int x = tmp[j];
                        ll len;
                        if (cirDpt[x] < cirTot[dcc_cnt] - cirDpt[x])
                            len = dis[dcc_cnt][cirDpt[x]];
                        else
                            len = cirSum[dcc_cnt] - dis[dcc_cnt][cirDpt[x]];
                        T.add(dcc_cnt + n, x, len);
                    }
                }
            }
        } else {
            low[u] = min(low[u], dfn[v]);
            if (dfn[v] < dfn[u])
                stack[++top] = i;
        }
    }
}

}

Bit_Tree<ll> s[3];  // tree prefix sum
int dpt[NN], fa[NN], timer, kthfa[lg2N][NN];
int idx[NN], st[lg2N][NN];
int L[NN], R[NN];

void dfs(int u) {
    st[0][idx[u] = ++timer] = u;
    L[u] = idx[u];
    for (int i = T.head[u]; i; i = T.edge[i].nxt) {
        int v = T.edge[i].v;
        ll w = T.edge[i].w;
        dpt[v] = dpt[u] + 1;
        fa[v] = kthfa[0][v] = u;
        
        dfs(v);
        
        if (u <= n) {
            
        } else if (w > 0) {
            s[0].modify(L[v], R[v], w);
            s[1].modify(L[v], R[v], cirSum[u - n] - w);
        } else {
            w = -w;
            s[0].modify(L[v], R[v], w);
            s[1].modify(L[v], R[v], w);
            s[2].modify(L[v], R[v], w);
        }
    }
    R[u] = timer;
}
inline int Min(int a, int b) {
    return dpt[a] < dpt[b] ? a : b;
}
inline int lca(int u, int v) {
    if (u == v) return u;
    if ((u = idx[u]) > (v = idx[v])) swap(u, v);
    int k = __lg(v - u++);
    return fa[Min(st[k][u], st[k][v - (1 << k) + 1])];
}
inline int jump(int u, int k) {
    for (int i = lg2N - 1; ~i; --i)
        if (k & 1 << i) u = kthfa[i][u];
    return u;
}

struct {
    int u, v, tp;
    int _u, _v;
} rd[N];  // Road

int bl[NN];  // 设 v 为 u 在虚树上的父亲，bl[u] 为 v 的一个在圆方树上的孩子，且为 u 的祖先
int cha[2][NN], _cha[2][NN];
vector<int> vec[NN];  // 方点 LCA 处的特殊处理
long long qans;

void redfs(int u) {
    if (u <= n) {
        for (int i = VT.head[u]; i; i = VT.edge[i].nxt) {
            int v = VT.edge[i].v;
            redfs(v);
            int w0 = cha[0][v], w1 = cha[1][v];
            cha[0][u] += w0;
            cha[1][u] += w1;
            long long x0 = s[0][idx[v]] - s[0][idx[u]];
            long long x1 = s[1][idx[v]] - s[1][idx[u]];
            long long x2 = s[2][idx[v]] - s[2][idx[u]];
            if (w0 && w1) {
                qans += x0 + x1 - x2;
            } else if (w0) {
                qans += x0;
            } else if (w1) {
                qans += x1;
            }
        }
    } else {
        for (int i = VT.head[u]; i; i = VT.edge[i].nxt) {
            int v = VT.edge[i].v;
            redfs(v);
            int w0 = cha[0][v], w1 = cha[1][v];
            long long x0 = s[0][idx[v]] - s[0][idx[bl[v]]];
            long long x1 = s[1][idx[v]] - s[1][idx[bl[v]]];
            long long x2 = s[2][idx[v]] - s[2][idx[bl[v]]];
            if (w0 && w1) {
                qans += x0 + x1 - x2;
            } else if (w0) {
                qans += x0;
            } else if (w1) {
                qans += x1;
            }
        }
        vector<pair<ll, int>> tmp;
        for (int id : vec[u]) {
            int uu = rd[id]._u;
            int vv = rd[id]._v;
            int tp = rd[id].tp;
            if (cirDpt[uu] > cirDpt[vv])
                swap(uu, vv);
            int A = cirDpt[vv] - cirDpt[uu];  // uu -> vv
            int B = cirTot[u - n] - A;  // uu -> head -> tail -> vv
            if (tp == (A > B)) {
                // A
                tmp.emplace_back(dis[u - n][cirDpt[uu]], 1);
                tmp.emplace_back(dis[u - n][cirDpt[vv]], -1);
            } else {
                // B
                tmp.emplace_back(0, 1);
                tmp.emplace_back(dis[u - n][cirDpt[uu]], -1);
                tmp.emplace_back(dis[u - n][cirDpt[vv]], 1);
            }
        }
        for (int i = VT.head[u]; i; i = VT.edge[i].nxt) {
            int v = VT.edge[i].v;
            int vv = bl[v];
            int w0 = cha[0][v], w1 = cha[1][v];
            w0 += _cha[0][vv], w1 += _cha[1][vv];
            cha[0][u] += w0;
            cha[1][u] += w1;
            int L = cirDpt[vv];
            int R = cirTot[u - n] - L;
            if (w0 && w1) {
                tmp.emplace_back(0, 1);
            } else if (w0 || w1) {
                if (bool(w0) == (L < R)) {
                    tmp.emplace_back(0, 1);
                    tmp.emplace_back(dis[u - n][cirDpt[vv]], -1);
                } else {
                    tmp.emplace_back(dis[u - n][cirDpt[vv]], 1);
                }
            }
        }
        sort(tmp.begin(), tmp.end());
        int m = tmp.size();
        int sum = 0;
        for (int i = 0, j = -1; i < m; i = j + 1) {
            while (j + 1 < m && tmp[j + 1].first == tmp[i].first)
                sum += tmp[++j].second;
            ll len;
            if (j == m - 1)
                len = cirSum[u - n] - tmp[i].first;
            else
                len = tmp[j + 1].first - tmp[i].first;
            if (sum) {
                qans += len;
            }
        }
    }
}

void query() {
    static int st[NN], _st[NN];
    int k;
    scanf("%d", &k);
    if (!k) {
        puts("0");
        return;
    }
    int m = 0;
    for (int i = 1; i <= k; ++i) {
        scanf("%d%d%d", &rd[i].u, &rd[i].v, &rd[i].tp);
        st[++m] = rd[i].u;
        st[++m] = rd[i].v;
    }
    sort(st + 1, st + m + 1, [] (int a, int b) {
        return idx[a] < idx[b];
    });
    for (int i = 1; i < m; ++i)
        st[m + i] = lca(st[i], st[i + 1]);
    sort(st + 1, st + m * 2, [] (int a, int b) {
        return idx[a] < idx[b];
    });
    m = unique(st + 1, st + m * 2) - st - 1;
    int _m = 0;
    for (int i = 1; i < m; ++i) {
        int u = st[i + 1], v = lca(st[i], st[i + 1]);
        VT.add(v, u);
        if (v > n) {
            int _u = jump(u, dpt[u] - dpt[v] - 1);
            _st[++_m] = _u;
            bl[u] = _u;
        }
    }
    for (int i = 1; i <= k; ++i) {
        int u = rd[i].u, v = rd[i].v, w = rd[i].tp;
        int p = lca(u, v);
        if (p > n) {
            int _u = jump(u, dpt[u] - dpt[p] - 1);
            int _v = jump(v, dpt[v] - dpt[p] - 1);
            ++cha[w][u], --_cha[w][_u];
            ++cha[w][v], --_cha[w][_v];
            rd[i]._u = _u;
            rd[i]._v = _v;
            vec[p].emplace_back(i);
        } else {
            ++cha[w][u], ++cha[w][v];
            cha[w][p] -= 2;
        }
    }
    qans = 0;
    redfs(st[1]);
    printf("%lld\n", qans);
    VT.tot = 1;
    for (int i = 1; i <= m; ++i) {
        int u = st[i];
        VT.head[u] = 0;
        vec[u].clear();
        cha[0][u] = cha[1][u] = 0;
    }
    for (int i = 1; i <= _m; ++i) {
        int u = _st[i];
        _cha[0][u] = _cha[1][u] = 0;
    }
}

void modify() {
    int w, x;
    scanf("%d%d", &w, &x);
    if (!w) return;
    int u = G.edge[w << 1].v;
    int v = G.edge[w << 1 | 1].v;
    int tw = G.edge[w << 1].w;
    if (dpt[u] > dpt[v]) swap(u, v);
    if (notInCir[w]) {
        s[0].modify(L[v], R[v], x - tw);
        s[1].modify(L[v], R[v], x - tw);
        s[2].modify(L[v], R[v], x - tw);
    } else {
        int o = fa[v] - n;
        int tot = cirTot[o];
        const auto& circle = ::circle[o];
        int lp = circle[tot / 2 - 1];
        int rp = circle[tot / 2];
        int hd = circle[0];
        int tl = circle[tot - 2];
        int whr;  // -1: left, 0: middle, 1: right
        if (u == fa[fa[v]]) {
            if (cirDpt[v] == 1)
                whr = -1;
            else
                whr = 1;
        } else {
            if (cirDpt[u] > cirDpt[v])
                swap(u, v);
            if (u == lp && v == rp) {
                whr = 0;
            } else {
                if (cirDpt[v] <= tot / 2)
                    whr = -1;
                else {
                    whr = 1;
                    swap(u, v);
                }
            }
        }
        if (whr == 0) {
            dis[o].modify(cirDpt[v], tot - 1, x - tw);
            s[1].modify(L[hd], R[lp], x - tw);
            s[1].modify(L[rp], R[tl], x - tw);
        } else if (whr == -1) {
            dis[o].modify(cirDpt[v], tot - 1, x - tw);
            s[0].modify(L[v], R[lp], x - tw);
            if (v != hd)
                s[1].modify(L[hd], R[u], x - tw);
            s[1].modify(L[rp], R[tl], x - tw);
        } else {
            s[0].modify(L[rp], R[v], x - tw);
            if (v != tl) {
                dis[o].modify(cirDpt[u], tot - 1, x - tw);
                s[1].modify(L[u], R[tl], x - tw);
            }
            s[1].modify(L[hd], R[lp], x - tw);
        }
        cirSum[o] += x - tw;
    }
    G.edge[w << 1].w = x;
    G.edge[w << 1 | 1].w = x;
}

int main() {
    scanf("%d%d%d", &n, &m, &q);
    for (int i = 1, u, v, w; i <= m; ++i) {
        scanf("%d%d%d", &u, &v, &w);
        G.add(u, v, w);
        G.add(v, u, w);
    }
    $build::tarjan(1, 0);
    for (int i = 0; i < 3; ++i)
        s[i].init(n + dcc_cnt);
    dfs(1);
    for (int k = 1; k < lg2N; ++k) {
        for (int i = 1; i + (1 << k) - 1 <= n + dcc_cnt; ++i)
            st[k][i] = Min(st[k - 1][i], st[k - 1][i + (1 << (k - 1))]);
        for (int i = 1; i <= n + dcc_cnt; ++i)
            kthfa[k][i] = kthfa[k - 1][kthfa[k - 1][i]];
    }
    while (q--) query(), modify();
    return 0;
}

类型五：静态仙人掌，动态维护全局信息

其实就是仙人掌上的 DDP 问题。

我们不妨从一个具体的问题开始思考：支持修改点权，动态维护仙人掌的最大独立集权值。

在树上，我们做过模板题，没有修改时，我们在前文例题一探讨过单次 \(\mathcal{O}(n)\) 求仙人掌最大独立集的算法，我们要做的就是把这两个算法结合起来。

回顾在一个序列上我们如何动态维护独立集的？设 \(f_0,f_1\) 表示选或不选最后一个元素的最大独立集，那么根据定义有 \(f_1'=f_0+a_i,f_0'=\max\{f_0,f_1\}\)，容易写出转移方程的 \((+,\max)\) 矩阵乘法形式：

\\\begin{bmatrix} f_0 \& f_1 \\end{bmatrix} \\times \\begin{bmatrix} 0 \& a_i \\\\ 0 \& -\\infty \\\\ \\end{bmatrix} = \\begin{bmatrix} f_0' \& f_1' \\end{bmatrix} \\

回顾这个东西是如何上树的。我们轻重链剖分后，重链其实就是普通的一条链，但是对于不选择 / 选择 \(u\) 的收益不再是 \(0/a_u\)，而是 \(t_0/t_1+a_u\)，其中 \(t_{0/1}\) 表示轻儿子对它的贡献，\(t_0\) 为所有轻儿子的 \(\max\{f_0,f_1\}\) 之和，\(t_1\) 为所有轻儿子的 \(f_0\) 之和。转移矩阵为：\(\begin{bmatrix} t_0 & t_1+a_u \\ t_0 & -\infty \\ \end{bmatrix}\)。如此，我们实际完成了，通过求一条以 \(u\) 为链顶的重链的矩阵乘法，得到 \(u\) 子树的答案。

这个东西怎么上仙人掌呢？无非就是考虑如何处理环。

目前状态肯定是不够了，想到把扩展状态成 \(f_0,f_1,g_0,g_1\)，分别对应环尾必不选和可能选的 DP 值。但是这是不好做的。如上图，假设这个点双对应的方点为 \(u\)，\(u\) 的父亲圆点为 \(1\)，重儿子为 \(5\)。为了转移顺序，我们也许会想到把 DFS 序设置为：

\7,6,\\colorbox{#409eff}{$ 5,... $},4,3,2 \\

但是 \(5,...\) 得到的是 \(5\) 的子仙人掌的 DP 值，我们并不能将它再乘上某一个矩阵，得到对应在 \(f_0,f_1,g_0,g_1\) 上的转移矩阵。所以这个想法是错误的。

以上想法错误之处，根本在于重儿子不能出现在转移方程的中间，否则无法通过 DP 值得到对应的转移矩阵。那么 \(5\) 作为 DP 的初始位置，应该如何设置转移顺序和状态呢？

我们想到一种「兵分两路」的转移方式，将环拆成两条链：\(5,6,7,1\) 和 \(5,4,3,2\)，并要求 \(5\) 要么同时选，要么同时不选，最后统计答案的时候 \(1,2\) 不能同时选。设 \(f_{a,b}\)，其中 \(a,b\) 分别表示左右两条链，目前考虑到的链顶选或不选的答案。初始矩阵为：

\\\begin{bmatrix} f_{0,0}\&f_{0,1}\&f_{1,0}\&f_{1,1} \\end{bmatrix} = \\begin{bmatrix} t_0\&-\\infty\&-\\infty\&t_1 \\end{bmatrix} \\

其中 \(t_{0/1}\) 表示重儿子 \(5\) 传统的 DP 值。这同时解决了 \(5\) 只能最多选一次的问题。

对于左边这条链上的点 \(u\)，会独立转移 \(f_{0/1,*}\)，即对于 \(p=0,1\)，\(f_{0,p}'=\max\{f_{0,p},f_{1,p}\}+t_0,f_{1,p}'=f_{0,p}+t_1\)，其中 \(t_{0/1}\) 表示 \(u\) 考虑其子仙人掌的传统 DP 值，下文在不引起歧义的前提下，省去了对 \(t_{0/1}\) 的解释。写成转移矩阵的形式就是：

\f(t_0,t_1,1)=\\begin{bmatrix} t_0 \& \& t_1 \& \\\\ \& t_0 \& \& t_1 \\\\ t_0 \& \& \& \\\\ \& t_0 \& \& \\\\ \\end{bmatrix} \\

同理，对于右边那条链上的 \(u\) 的转移为：

\f(t_0,t_1,2)=\\begin{bmatrix} t_0 \& t_1 \& \& \\\\ t_0 \& \& \& \\\\ \& \& t_0 \& t_1 \\\\ \& \& t_0 \& \\\\ \\end{bmatrix} \\

在 \(1\) 点，我们就能求出想要的值，不妨令 \(1\) 在左侧链上，那么 \(t_0=\max\{f_{0,0},f_{0,1}\},t_1=f_{1,0}\)，我们可以写出一个矩阵，通过 \(\begin{bmatrix} f_{0,0}&f_{0,1}&f_{1,0}&f_{1,1} \end{bmatrix}\) 得到 \(\begin{bmatrix} t_0&-\infty&-\infty&t_1 \end{bmatrix}\)，这是正是环上 DP 的初始值，从而形成逻辑上的闭环。

\M=\\begin{bmatrix} 0 \& \& \& \\\\ 0 \& \& \& \\\\ \& \& \& 0 \\\\ \& \& \& \\end{bmatrix} \\

当然，以上所有矩阵都是转移矩阵，我们初始矩阵为：

\M_0=\\begin{bmatrix} 0 \& \& \& 0 \\end{bmatrix} \\

我们已经初步确认，这个问题是可做的，并且粗浅地想出了一种转移的方式。接下来，需要解决遗留下来尚未处理的细节。

1. 如何设计 DFS 序？

   类似类型三的 DFS 序设计，将方点替换为其所有轻孩子，接着是重儿子和它的子树。同时，我们需要左链右链上的节点的相对顺序满足转移顺序。

   

   例如，用不同颜色区分左右链，上图的一个不合法 的 DFS 序为 \({\color{red}1},{\color{red}7},{\color{yellow}2},{\color{yellow}4},{\color{red}6},{\color{yellow}3},5\)，因为右链转移顺序并不是 \(3,4,2\)，而应该是 \(4,3,2\)。一种合法的 DFS 序为 \({\color{red}1},{\color{red}7},{\color{yellow}2},{\color{yellow}3},{\color{red}6},{\color{yellow}4},5\)。当然，我们显然喜欢更简单的 DFS 序 \({\color{red}1},{\color{red}7},{\color{red}6},{\color{yellow}2},{\color{yellow}3},{\color{yellow}4},5\)，它先按照顺序转移完了右链上的 \(4,3,2\)，再转移完左链上 \(6,7,1\)。

2. 如何分配 DFS 序上对应转移矩阵？

   先来明确一下各种 DFS 序区间和其对应矩阵的关系。

   对于一个方点，它对应 DFS 序上的区间求出来的矩阵，是一个环上 DP 未完成的矩阵，因为缺少了链顶的转移。例如，\({\color{red}1},{\color{red}7},{\color{red}6},{\color{yellow}2},{\color{yellow}3},{\color{yellow}4},5\) 中，实际方点对应的 DFS 序为 \({\color{red}7},{\color{red}6},{\color{yellow}2},{\color{yellow}3},{\color{yellow}4},5\)，这缺少了 \({\color{red}1}\) 的转移。

   对于一个重儿子圆点，它对应 DFS 序上的区间求出来的矩阵，已经完成了环上的转移，左乘 \(M_0\) 后形如 \(\begin{bmatrix}t_0&-\infty&-\infty&t_1\end{bmatrix}\)。

   对于一个轻儿子圆点，它没有对应的 DFS 序区间。

   类似树上，维护 \(u\) 所有轻儿子的答案和，记为 \(g_0,g_1\)，以及不妨令 \(g_1\) 中包含 \(u\) 的点权。

   1. \(u\) 为重儿子。

      它在 DFS 序上位置形如：\(...,u,(a),(b_1),(b_2),...\)，其中 \((a)\) 为 \(u\) 的重方儿子对应子树，\((b_i)\) 对应 \(u\) 的轻方儿子的子树，两个 \(...\) 分别对应 \(u\) 的轻儿子兄弟，和这些点的方儿子子树。

      \((a)\) 求出来一个环上 DP 未完成的矩阵，所以要先乘上 \(f(g_0,g_1,1)\) 完成环上 DP，再乘上 \(M\)，得到形如 \(\begin{bmatrix}t_0&-\infty&-\infty&t_1\end{bmatrix}\) 的矩阵。这也就是 \(u,(a)\) 求出的结果。

   2. \(u\) 为轻儿子。

      先将 \(g_0,g_1\) 加上其重儿子的贡献，然后它在 DFS 序上的矩阵即为 \(f(g_0,g_1,\operatorname{type}(u))\)。

3. 如何求答案？

   \(1\) 为链顶的这条重链，对应的区间的矩阵之积，就是转移矩阵，左乘 初始矩阵 \(M_0\) 得到答案矩阵 \(\begin{bmatrix}t_0&-\infty&-\infty&t_1\end{bmatrix}\)，答案即为 \(\max\{t_0,t_1\}\)。

4. 如何修改？

   树上修改的时候，设当前点为 \(u\)，其重链顶为 \(v\)，\(v\) 的父亲为 \(w\)，那么要先在 \(w\) 的矩阵中减去这条重链的贡献，再加上修改后的贡献，接着令 \(u\gets w\)，继续操作，直到 \(v=1\) 停止。上述过程中要求我们维护一个 \(M_{\mathrm{last}}\) 表示以 \(v\) 为链顶的这条重链修改前的矩阵之积。在修改 \(w\) 前要先求出 \(w\) 所在重链的矩阵之积，以赋值给 \(M_{\mathrm{last}}\)。

   仙人掌上，对于 \(v\) 的类型分类讨论。

   1. \(v\) 为圆点。

      我们需要处理 \(v\) 的转移矩阵。\(v\) 的 \(g_0,g_1\) 可以方便维护，那么只需要和初始化的时候一样，求出重儿子的贡献，在线段树上修改即可。发现竟然不需要 \(M_{\mathrm{last}}\) 之类的东西。

   2. \(v\) 为方点。

      我们需要处理 \(w\) 的转移矩阵。\(v\) 作为 \(w\) 的轻儿子，就需要在 \(w\) 的 \(g_0,g_1\) 中，减去原先的贡献，再加上修改后的贡献。于是类似树上 DDP，需要维护 \(M_{\mathrm{last}}\)，接着，按照 \(w\) 为重儿子还是轻儿子，修改其转移矩阵即可。

   如何维护 \(M_{\mathrm{last}}\)？似乎只需要和树上 DDP 类似，当 \(w\) 链顶 \(p\) 为方点时，先查询 \(p\) 对应的转移矩阵，赋值给 \(M_{\mathrm(last)}\) 即可。但这在某种情况下是错误的。当 \(u=v\) 为圆点时，我们查询 \(p\) 的转移矩阵时，会包含 \(u\) 的转移矩阵，我们能够保证这个矩阵是没有更新过的吗？不能，因为可能上一次操作为情况 2「\(v\) 为方点」，而这会更新到 \(u\) 的转移矩阵，所以我们需要在上一次操作，提前判断这种特殊情况，提前赋值 \(M_{\mathrm{last}}\)，在这一次操作就不对 \(M_{\mathrm{last}}\) 赋值。具体可以参考例题代码。

我们至此成功解决了这个问题，时间复杂度 \(\mathcal{O}(nw^3\log n+qw^3\log^2n)\)，其中 \(w=4\) 为矩阵的大小。或许使用全局平衡二叉树可以优化到一只 \(\log\)，但是没有实现。

我们在上文中探讨了一种经典的 DDP 问题在仙人掌上的求解方式，对于其他 DDP 问题，或许可以参考这种方式解决问题。
例十、DDP on cactus（洛谷） Problem Statement

\(n\) 个点 \(m\) 条边的仙人掌，点编号为 \(1\sim n\)，每个结点有一个权值 \(w_u\)。

\(q\) 次点权修改操作，你需要在第一次修改前以及每次修改后，输出这棵仙人掌的最大独立集。

\(2\leq n\leq10^5\)。\(1\leq q\leq 10^5\)。任意时刻 \(0\leq w_i\leq 10^9\)。
Problem Analysis

前文分析的仙人掌上最大独立集问题。给出了一种参考实现。
Solution

#include <cstdio>
#include <iostream>
#include <cstring>
#include <cassert>
using namespace std;

using ll = long long;

const int N = 1e5 + 10;
const int M = 2e5 + 10;
const int N2 = N << 1;
const ll oinf = 0xc1c1c1c1c1c1c1c1;

int n, m, q;
int val[N];

template <size_t _N, size_t _M>
class Graph {
public:
    Graph(): tot(1) {}
    struct node {
        int v, nxt;
    } edge[_M];
    int head[_N], tot;
    void add(int u, int v) {
        edge[++tot] = { v, head[u] };
        head[u] = tot;
    }
};

Graph<N, M << 1> G;
Graph<N2, N2> T;

int dcc_cnt;

namespace $build {

int dfn[N], low[N], timer;
int stack[N], top;

void tarjan(int u, int fr) {
    dfn[u] = low[u] = ++timer;
    stack[++top] = u;
    for (int i = G.head[u]; i; i = G.edge[i].nxt) {
        if (i == (fr ^ 1)) continue;
        int v = G.edge[i].v;
        if (!dfn[v]) {
            tarjan(v, i);
            low[u] = min(low[u], low[v]);
            if (low[v] >= dfn[u]) {
                ++dcc_cnt;
                T.add(u, dcc_cnt + n);
                while (true) {
                    int x = stack[top--];
                    T.add(dcc_cnt + n, x);
                    if (x == v) break;
                }
            }
        } else {
            low[u] = min(low[u], dfn[v]);
        }
    }
}

}

inline ll max(ll a, ll b) {
    return a > b ? a : b;
}
struct Matrix {
    ll v[4][4];
    void init() { memset(v, 0xc1, sizeof(v)); }
    void unit() { v[0][0] = v[1][1] = v[2][2] = v[3][3] = 0; }
    ll* operator [] (int x) { return v[x]; }
    ll const* operator [] (int x) const { return v[x]; }
    friend inline Matrix operator * (const Matrix& a, const Matrix& b) {
        Matrix c;
        c[0][0] = max(oinf, max(max(a[0][0] + b[0][0], a[0][1] + b[1][0]), max(a[0][2] + b[2][0], a[0][3] + b[3][0])));
        c[0][1] = max(oinf, max(max(a[0][0] + b[0][1], a[0][1] + b[1][1]), max(a[0][2] + b[2][1], a[0][3] + b[3][1])));
        c[0][2] = max(oinf, max(max(a[0][0] + b[0][2], a[0][1] + b[1][2]), max(a[0][2] + b[2][2], a[0][3] + b[3][2])));
        c[0][3] = max(oinf, max(max(a[0][0] + b[0][3], a[0][1] + b[1][3]), max(a[0][2] + b[2][3], a[0][3] + b[3][3])));
        c[1][0] = max(oinf, max(max(a[1][0] + b[0][0], a[1][1] + b[1][0]), max(a[1][2] + b[2][0], a[1][3] + b[3][0])));
        c[1][1] = max(oinf, max(max(a[1][0] + b[0][1], a[1][1] + b[1][1]), max(a[1][2] + b[2][1], a[1][3] + b[3][1])));
        c[1][2] = max(oinf, max(max(a[1][0] + b[0][2], a[1][1] + b[1][2]), max(a[1][2] + b[2][2], a[1][3] + b[3][2])));
        c[1][3] = max(oinf, max(max(a[1][0] + b[0][3], a[1][1] + b[1][3]), max(a[1][2] + b[2][3], a[1][3] + b[3][3])));
        c[2][0] = max(oinf, max(max(a[2][0] + b[0][0], a[2][1] + b[1][0]), max(a[2][2] + b[2][0], a[2][3] + b[3][0])));
        c[2][1] = max(oinf, max(max(a[2][0] + b[0][1], a[2][1] + b[1][1]), max(a[2][2] + b[2][1], a[2][3] + b[3][1])));
        c[2][2] = max(oinf, max(max(a[2][0] + b[0][2], a[2][1] + b[1][2]), max(a[2][2] + b[2][2], a[2][3] + b[3][2])));
        c[2][3] = max(oinf, max(max(a[2][0] + b[0][3], a[2][1] + b[1][3]), max(a[2][2] + b[2][3], a[2][3] + b[3][3])));
        c[3][0] = max(oinf, max(max(a[3][0] + b[0][0], a[3][1] + b[1][0]), max(a[3][2] + b[2][0], a[3][3] + b[3][0])));
        c[3][1] = max(oinf, max(max(a[3][0] + b[0][1], a[3][1] + b[1][1]), max(a[3][2] + b[2][1], a[3][3] + b[3][1])));
        c[3][2] = max(oinf, max(max(a[3][0] + b[0][2], a[3][1] + b[1][2]), max(a[3][2] + b[2][2], a[3][3] + b[3][2])));
        c[3][3] = max(oinf, max(max(a[3][0] + b[0][3], a[3][1] + b[1][3]), max(a[3][2] + b[2][3], a[3][3] + b[3][3])));
        return c;
    }
    void output() const {
        for (int i = 0; i < 4; ++i) {
            for (int j = 0; j < 4; ++j) {
                if (v[i][j] <= -10000000)
                    printf("-inf ");
                else
                    printf("%lld ", v[i][j]);
            }
            puts("");
        }
    }
};
using mat_t = Matrix;

int siz[N2], son[N2];
int fa[N2], top[N2], tail[N2];

int dfn[N], idx[N], L[N2], R[N2], timer;
int typ[N];
/**
 * u is yuan:
 *      [L[u], R[u]] = subtree(u)
 *      typ[u] = { 0: son, 1: F, 2: G }
 * u is fang:
 *      [L[u], R[u]] = son(u)
*/

void dfs(int u) {
    siz[u] = 1;
    for (int i = T.head[u]; i; i = T.edge[i].nxt) {
        int v = T.edge[i].v;
        fa[v] = u;
        dfs(v), siz[u] += siz[v];
        if (siz[v] > siz[son[u]])
            son[u] = v;
    }
}

const mat_t ans2init = {{
    { 0   , oinf, oinf, oinf },
    { 0   , oinf, oinf, oinf },
    { oinf, oinf, oinf, 0    },
    { oinf, oinf, oinf, oinf },
}};

const mat_t beginst = {{
    { 0   , oinf, oinf, 0    },
    { oinf, oinf, oinf, oinf },
    { oinf, oinf, oinf, oinf },
    { oinf, oinf, oinf, oinf },
}};

inline mat_t getmat(ll t0, ll t1, int c) {
    mat_t m;
    m.init();
    if (c == 1) {
        m[0][0] = m[1][1] = m[2][0] = m[3][1] = t0;
        m[0][2] = m[1][3] = t1;
    } else {
        m[0][0] = m[1][0] = m[2][2] = m[3][2] = t0;
        m[0][1] = m[2][3] = t1;
    }
    return m;
}

namespace $yzh {

#define ls (u << 1)
#define rs (u << 1 | 1)

mat_t tr[N << 2];

void _upd(int u, int l, int r, int p, const mat_t& mat) {
    if (l == r) {
        tr[u] = mat;
        return;
    }
    int mid = (l + r) >> 1;
    if (p <= mid) _upd(ls, l, mid, p, mat);
    else _upd(rs, mid + 1, r, p, mat);
    tr[u] = tr[rs] * tr[ls];
}

mat_t _qry(int u, int trl, int trr, int l, int r) {
    if (l <= trl && trr <= r) return tr[u];
    int mid = (trl + trr) >> 1;
    if (r <= mid) return _qry(ls, trl, mid, l, r);
    if (l >  mid) return _qry(rs, mid + 1, trr, l, r);
    return _qry(rs, mid + 1, trr, l, r) * _qry(ls, trl, mid, l, r);
}

void upd(int p, const mat_t& mat) { _upd(1, 1, n, p, mat); }
mat_t query(int l, int r) { return _qry(1, 1, n, l, r); }

#undef ls
#undef rs

}

ll f[2][N];

void redfs(int u, int tp) {
    top[u] = tp;
    tail[tp] = u;
    if (u <= n) {
        L[u] = timer + 1;
        ll f0 = 0, f1 = val[u];
        if (son[u]) redfs(son[u], tp);
        for (int i = T.head[u]; i; i = T.edge[i].nxt) {
            int v = T.edge[i].v;
            if (v == son[u]) continue;
            redfs(v, v);
            mat_t res = beginst * $yzh::query(L[v], idx[tail[v]]);
            res = res * getmat(0, 0, 1) * ans2init;
            f0 += res[0][0];
            f1 += res[0][3];
        }
        f[0][u] = f0;
        f[1][u] = f1;
        if (typ[u] != 0) {
            if (son[u]) {
                mat_t res = beginst * $yzh::query(L[son[u]], idx[tail[u]]);
                res = res * getmat(0, 0, 1) * ans2init;
                f0 += res[0][0], f1 += res[0][3];
            }
            /*
            also:
            mat_t res = beginst;
            if (son[u])
                res = res * $yzh::query(L[son[u]], idx[tail[u]]);
            res = res * getmat(f0, f1, 1) * ans2init;
            f0 = res[0][0], f1 = res[0][3];
            */
            
            $yzh::upd(idx[u], getmat(f0, f1, typ[u]));
        } else {
            $yzh::upd(idx[u], getmat(f0, f1, 1) * ans2init);
        }
        R[u] = timer;
    } else {
        L[u] = timer + 1;
        static int stk[N];
        int top = 0, i;
        for (i = T.head[u]; i; i = T.edge[i].nxt) {
            int v = T.edge[i].v;
            if (v == son[u]) break;
            dfn[idx[v] = ++timer] = v;
            typ[v] = 2;
        }
        for (i = T.edge[i].nxt; i; i = T.edge[i].nxt) {
            int v = T.edge[i].v;
            stk[++top] = v;
        }
        while (top) {
            int v = stk[top--];
            dfn[idx[v] = ++timer] = v;
            typ[v] = 1;
        }
        dfn[idx[son[u]] = ++timer] = son[u];
        typ[son[u]] = 0;
        R[u] = timer;
        redfs(son[u], tp);
        for (int i = T.head[u]; i; i = T.edge[i].nxt) {
            int v = T.edge[i].v;
            if (v == son[u]) continue;
            redfs(v, v);
        }
    }
}

void solve() {
    mat_t res = beginst * $yzh::query(idx[1], idx[tail[1]]);
    ll t0 = res[0][0], t1 = res[0][3];
    ll ans = max(t0, t1);
#ifdef XuYueming
    printf(">>>>>>>>>>>>>> ");
#endif
    printf("%lld\n", ans);
}

void modify(int u, int w) {
    mat_t lst;
    bool flag = false;
    {
        f[1][u] += w - val[u], val[u] = w;
        int v = top[u];
        if (v > n)
            lst = $yzh::query(L[v], idx[tail[v]]);
        else if (u == v) {
            int p = top[fa[v]];
            if (p > n)
                lst = $yzh::query(L[p], idx[tail[p]]), flag = true;
        }
        ll f0 = f[0][u], f1 = f[1][u];
        if (typ[u] != 0) {
            mat_t res = beginst;
            if (son[u])
                res = res * $yzh::query(L[son[u]], idx[tail[u]]);
            res = res * getmat(f0, f1, 1) * ans2init;
            $yzh::upd(idx[u], getmat(res[0][0], res[0][3], typ[u]));
        } else {
            $yzh::upd(idx[u], getmat(f0, f1, 1) * ans2init);
        }
    }
    while (top[u] != 1) {
        int v = top[u];
        int w = fa[v];
        
        if (v > n) {
            assert(flag == false);
            ll &f0 = f[0][w], &f1 = f[1][w];
            {
                mat_t res = beginst * lst;
                res = res * getmat(0, 0, 1) * ans2init;
                f0 -= res[0][0];
                f1 -= res[0][3];
            }
            {
                mat_t res = beginst * $yzh::query(L[v], idx[tail[v]]);
                res = res * getmat(0, 0, 1) * ans2init;
                f0 += res[0][0];
                f1 += res[0][3];
            }
            int p = top[w];
            if (p > n)
                lst = $yzh::query(L[p], idx[tail[p]]);
            else if (w == p) {
                p = top[fa[p]];
                if (p > n) {
                    lst = $yzh::query(L[p], idx[tail[p]]), flag = true;
                }
            }
            if (typ[w] != 0) {
                mat_t res = beginst;
                if (son[w])
                    res = res * $yzh::query(L[son[w]], idx[tail[w]]);
                res = res * getmat(f0, f1, 1) * ans2init;
                $yzh::upd(idx[w], getmat(res[0][0], res[0][3], typ[w]));
            } else {
                $yzh::upd(idx[w], getmat(f0, f1, 1) * ans2init);
            }
        } else {
            ll f0 = f[0][v], f1 = f[1][v];
            assert(typ[v] != 0);
            int p = top[w];
            if (p > n) {
                assert(flag == (u == v));
                if (flag) flag = false;
                else lst = $yzh::query(L[p], idx[tail[p]]);
            }
            mat_t res = beginst;
            if (son[v])
                res = res * $yzh::query(L[son[v]], idx[tail[v]]);
            res = res * getmat(f0, f1, 1) * ans2init;
            f0 = res[0][0], f1 = res[0][3];
            $yzh::upd(idx[v], getmat(f0, f1, typ[v]));
        }
        u = w;
    }
}

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1, u, v; i <= m; ++i) {
        scanf("%d%d", &u, &v);
        G.add(u, v), G.add(v, u);
    }
    for (int i = 1; i <= n; ++i) {
        scanf("%d", &val[i]);
    }
    $build::tarjan(1, 0);
    dfs(1);
    dfn[idx[1] = ++timer] = 1;
    typ[1] = 0;
    redfs(1, 1);
    
    scanf("%d", &q);
    solve();
    for (int u, w; q--; ) {
        scanf("%d%d", &u, &w);
        modify(u, w);
        solve();
    }
    return 0;
}

/*
15:25        static tree
day2 10:11   static cactus
day2 20:55   dynamic cactus
*/

Gen

#include <cstdio>
#include <iostream>
#include <vector>
#include <random>
#include <chrono>
using namespace std;

/* =========== Parameter =========== */

const int SEED = chrono::system_clock::now().time_since_epoch().count();

bool multiedge = true;
bool onlyOddCircle = false;

int MULTI_P = 50;

// int LEN = 1e4;
// int LEN = 4;

/* =========== Parameter =========== */

void _err(const char* msg, int lineNum) {
    fprintf(stderr, "Error at line #%d: %s\n", lineNum, msg);
    exit(1);
}
#define err(msg) _err(msg, __LINE__)

inline int rand(int l, int r) {
    static mt19937 rnd(SEED);
    if (l > r) err("invalid range");
    return l + rnd() % (r - l + 1);
}

int n = rand(99990, 100000);
int q = 100000;
int ROUND = 5;
int LEN = rand(1000, 1314);

// int n = rand(9500, 10000);
// // int n = 20;
// int q = 100000;
// int ROUND = 5;

// int LEN = rand(3, 1314);

int m_limit = -1;  // -1 for not limit

vector<pair<int, int>> edges;
vector<vector<int>> son(n, vector<int>());
vector<int> dpt(n);

int maxcir = LEN;
int chong = 0;

void dfs(int u) {
    for (size_t i = 0; i < son[u].size(); ++i) {
        int v = son[u][i];
        dpt[v] = dpt[u] + 1;
        dfs(v);
    }
}

int redfs(int u, int ban) {
    int res = u;
    int cnt = 0;
    for (size_t i = 0; i < son[u].size(); ++i) {
        int v = son[u][i];
        dpt[v] = dpt[u] + 1;
        if (v == ban) continue;
        int t = redfs(v, -1);
        int len = dpt[t] - dpt[u] + 1;
        if ((t != v || (multiedge && cnt < 2 && rand(0, MULTI_P) == 0))
                && (len % 2 == 1 || !onlyOddCircle)
                && (m_limit == -1 || (int)edges.size() < m_limit))
            edges.emplace_back(u, t), cnt += t == v, maxcir = max(maxcir, len), chong += t == v;
        else if (rand(0, son[u].size()) == 0 || dpt[t] > dpt[res])
            res = t;
    }
    return res;
}

int main() {
    // freopen(".\\testdata\\4.in", "w", stdout);
    
    // freopen("yzh", "w", stdout);
    // freopen("in", "w", stdout);
    
    if (n < 1) err("n shouldn't be less than 1");
    if (m_limit != -1 && m_limit < n - 1)
        err("m_limit shouldn't less than n-1");
    if (LEN > n)
        err("LEN too long");
    
    vector<int> id(n);
    for (int i = 0; i < n; ++i) id[i] = i;
    for (int i = 1; i < n; ++i)
        swap(id[i], id[rand(0, i)]);
    
    for (int i = 1; i < LEN; ++i) {
        int fa = i - 1;
        edges.emplace_back(fa, i);
        son[fa].emplace_back(i);
    }
    for (int i = LEN; i < n; ++i) {
        int fa = rand(0, i - 1);
        edges.emplace_back(fa, i);
        son[fa].emplace_back(i);
    }
    if (LEN > 1 && m_limit != n - 1) {
        edges.emplace_back(0, LEN - 1);
    }
    dfs(0);
    for (int i = 1; i < LEN; ++i)
        redfs(i - 1, i);
    redfs(LEN - 1, -1);
    
    for (size_t i = 1; i < edges.size(); ++i)
        swap(edges[i], edges[rand(0, i)]);
    
    printf("%d %d\n", n, (int)edges.size());
    for (size_t i = 0; i < edges.size(); ++i) {
        int u = edges[i].first;
        int v = edges[i].second;
        if (rand(0, 1)) swap(u, v);
        u = id[u], v = id[v];
        printf("%d %d\n", u + 1, v + 1);
    }
    
    const int maxV = 1e9;
    const int minV = 100;
    
    for (int i = 1; i <= n; ++i)
        printf("%d%c", rand(0, minV), " \n"[i == n]);
    
    printf("%d\n", q);
    if (ROUND) {
        if (q % (ROUND * 2)) throw;
        int t = q / (ROUND * 2);
        vector<int> vec;
        while (t--) {
            for (int i = 1; i <= ROUND; ++i) {
                int u = rand(1, n);
                printf("%d %d\n", u, rand(0, maxV));
                vec.emplace_back(u);
            }
            for (int i = 1; i <= ROUND; ++i) {
                if (rand(0, 1000) && !vec.empty()) {
                    int u = vec.back();
                    vec.pop_back();
                    printf("%d %d\n", u, rand(0, minV));
                } else {
                    int u = rand(1, n);
                    printf("%d %d\n", u, rand(0, maxV));
                    vec.emplace_back(u);
                }
            }
        }
    } else {
        for (int i = 1; i <= q; ++i) {
            printf("%d %d\n", rand(1, n), rand(0, maxV));
        }
    }
    
    fprintf(stderr, "Success!\n");
    fprintf(stderr, "n = %d, m = %d\n", n, (int)edges.size());
    fprintf(stderr, "circle = %d\n", (int)edges.size() - (n - 1));
    fprintf(stderr, "maxcir = %d\n", maxcir);
    fprintf(stderr, "chong = %d\n", chong);
    return 0;
}

#include <cstdio>
#include <iostream>
#include <vector>
#include <algorithm>
#include <cassert>
#include <random>
#include <chrono>
using namespace std;

const int SEED = chrono::system_clock::now().time_since_epoch().count();

inline int rand(int l, int r) {
    static mt19937 rnd(SEED);
    if (l > r) throw "invalid range";
    return l + rnd() % (r - l + 1);
}

int q = 1e5;
int ROUND = 5;

int n = 1e5, pts;
vector<pair<int, int>> edges;

int solve(int tot) {
    if (tot == 1)
        return ++pts;
    --tot;
    int du;
    if (rand(0, 4)) du = 2;
    else if (rand(0, 3)) du = 3;
    else du = 4;
    if (du > tot) du = tot;
    int one = tot / du;
    int u = ++pts;
    vector<int> son;
    for (int i = 1; i <= du - 1; ++i) {
        int v = solve(one);
        son.emplace_back(v);
    }
    {
        int v = solve(tot - (du - 1) * one);
        son.emplace_back(v);
    }
    edges.emplace_back(u, son.front());
    edges.emplace_back(son.back(), u);
    for (int i = 1; i < (int)son.size(); ++i)
        edges.emplace_back(son[i - 1], son[i]);
    return u;
}

int main() {
    solve(n);
    if (pts != n) throw;
    
    int m = edges.size();
    assert(n - 1 <= m && m <= 2 * (n - 1));
    
    for (size_t i = 1; i < edges.size(); ++i) {
        swap(edges[i], edges[rand(0, i)]);
    }
    
    vector<int> id(n);
    for (int i = 0; i < n; ++i) id[i] = i;
    for (int i = 1; i < n; ++i) {
        swap(id[i], id[rand(0, i)]);
    }
    
    printf("%d %d\n", n, (int)edges.size());
    for (size_t i = 0; i < edges.size(); ++i) {
        int u = edges[i].first;
        int v = edges[i].second;
        if (rand(0, 1)) swap(u, v);
        u = id[u - 1], v = id[v - 1];
        printf("%d %d\n", u + 1, v + 1);
    }
    
    const int maxV = 1e9;
    const int minV = 100;
    
    for (int i = 1; i <= n; ++i)
        printf("%d%c", rand(0, minV), " \n"[i == n]);
    
    printf("%d\n", q);
    if (q % (ROUND * 2)) throw;
    int t = q / (ROUND * 2);
    vector<int> vec;
    while (t--) {
        for (int i = 1; i <= ROUND; ++i) {
            int u = rand(1, n);
            printf("%d %d\n", u, rand(0, maxV));
            vec.emplace_back(u);
        }
        for (int i = 1; i <= ROUND; ++i) {
            if (rand(0, 1000) && !vec.empty()) {
                int u = vec.back();
                vec.pop_back();
                printf("%d %d\n", u, rand(0, minV));
            } else {
                int u = rand(1, n);
                printf("%d %d\n", u, rand(0, maxV));
                vec.emplace_back(u);
            }
        }
    }
    
    fprintf(stderr, "Success!\n");
    fprintf(stderr, "n = %d, m = %d\n", n, (int)edges.size());
    fprintf(stderr, "circle = %d\n", (int)edges.size() - (n - 1));
    return 0;
}

类型六：动态仙人掌

删边连边，保证操作前后都是森林，这类动态树问题，我们使用 LCT，SATT 等方式维护原树。

删边连边，保证操作前后都是沙漠，这类动态仙人掌问题，我们使用 LCT，SATT 等方式维护圆方树。

笔者能力有限，以后有时间再来补这一部分。

拓展：多层仙人掌

既然仙人掌的形态很像把树上节点替换成环，我们可以尝试把树上每个节点换成一棵仙人掌，如此进行下去，得到多层仙人掌的结构。

熟悉了仙人掌，其实这种结构无非是仙人掌的小拓展罢了，可以使用类似的算法解决。

圆方树在「一般无向图」上的应用

相信你已经掌握了如何使用圆方树解决仙人掌的问题，接下来我们将更进一步，学习如何在一般无向图上应用圆方树。

相比仙人掌而言，一般无向图并没有许多良好的性质，问题并不难于仙人掌上对应类型的问题。

类型一：单次询问整体信息

例十一、APIO2018 铁人两项（洛谷） Problem Statement

给你一张有 \(n\) 个点和 \(m\) 条边的无向图，你需要统计有序三元组 \((s,c,f)\) 的个数，且需要满足存在一条简单路径依次经过 \(s,c,f\)。简单路径指不重复经过点的路径。

\(n\leq 10^5\)，\(m\leq 2\times 10^5\)。
Problem Analysis

考虑在树上统计三元组的个数。不妨将 \(s,f\) 视为地位相等的「端点」，最后答案乘以二即可。设 \(g_u\) 表示 \(u\) 子树中选出一个端点的方案数，其实就是 \(u\) 为根的子树大小。再设 \(f_u\) 表示 \(u\) 子树中选出一个端点 \(v\)，再在 \(v\sim u\) 这条路径上选出中间点 \(c\) 的方案数。\(g\) 的转移显然。\(f\) 的转移也很简单，分为选不选择 \(u\) 为 \(c\) 两种情况讨论。对于一个 \(v\in \operatorname{son}(u)\)，若选择，\(f_u\Leftarrow g_v\)；若不选择，\(f_u\Leftarrow f_v\)。其中 \(a\Leftarrow b\) 表示 \(a\gets a+b\)。那么如何统计答案呢？我们考虑不断合并子树的过程，\(f_u,g_u\) 的含义为 \(u\) 和已经考虑过的子树，构成的一棵以 \(u\) 为根子树的信息。注意这个子树和传统意义上以 \(u\) 为根的子树之间的区别。考虑这个子树和一个没被合并进来的，以 \(v\) 为根的子树，它们之间对答案产生的贡献。显然就是 \(f_u\cdot g_v+f_v\cdot g_u\)，加号前表示 \(c\) 落在以 \(u\) 为根的子树中，加号后表示 \(c\) 落在以 \(v\) 为根的子树中，然后运用加法原理即可，这是不重不漏的。

放到无向图上呢？我们考虑无非就是选取 \(c\) 的这一步变得有些复杂------在一个点双中选点而不是在一个点上选点。分为如何转移和如何统计答案两部分思考。记这个点双大小为 \(m\)。转移很不难想到，设方点的父亲圆点为 \(u\)，某一个孩子圆点为 \(v\)，\(g_u\Leftarrow g_v\)，\(f_u\Leftarrow f_v + (m-1)g_v\)，这里 \(m-1\) 的系数表示，\(c\) 可以选择除了 \(v\) 以外任意一个点双中的点，对于 \(c=v\) 的情况已经统计在 \(f_v\) 内了。我们先考虑暴力统计答案，枚举 \(m\) 个圆点中两个不同的圆点 \(u,v\)，然后一样按照 \(c\) 放在哪里分类讨论。\(c\) 在 \(u\) 那一边，\(ans\Leftarrow g_u\cdot f_v\)；\(c\) 在 \(v\) 那一边，\(ans\Leftarrow g_v\cdot f_u\)；\(c\) 在点双中除了 \(u,v\) 其他的点上，\(ans\Leftarrow g_u\cdot g_v \cdot(m-2)\)。优化到线性也很简单，用类似前缀和的方法维护 \(\sum f_v\) 和 \(\sum g_v\) 即可。

时空复杂度 \(\mathcal{O}(n+m)\)。

注意此题坑点：图可能不连通，对每一个连通块做一遍即可。
Solution

#include <cstdio>
#include <iostream>
#include <vector>
using namespace std;

const int N = 1e5 + 10;
const int M = 2e5 + 10;

int n, m;

struct node {
    int v, nxt;
} edge[M << 1];
int head[N], tot = 1;
void add(int u, int v) {
    edge[++tot] = { v, head[u] };
    head[u] = tot;
}

int dfn[N], low[N], timer;
int stack[N], top;

long long f[N], g[N], ans;

void tarjan(int u, int fr) {
    g[u] = 1;
    dfn[u] = low[u] = ++timer;
    stack[++top] = u;
    for (int i = head[u]; i; i = edge[i].nxt) {
        if (i == (fr ^ 1)) continue;
        int v = edge[i].v;
        if (!dfn[v]) {
            tarjan(v, i);
            low[u] = min(low[u], low[v]);
            if (low[v] >= dfn[u]) {
                vector<int> scc;
                while (true) {
                    int x = stack[top--];
                    scc.emplace_back(x);
                    if (x == v) break;
                }
                scc.emplace_back(u);
                int m = scc.size();
                
                long long sf = 0, sg = 0;
                for (int j = 0; j < m; ++j) {
                    int u = scc[j];
                    ans += g[u] * sf + sg * f[u];
                    ans += (m - 2) * g[u] * sg;
                    sf += f[u], sg += g[u];
                }
                // for (int a = 0; a < m; ++a)
                //     for (int b = a + 1; b < m; ++b) {
                //         int u = scc[a], v = scc[b];
                //         ans += g[u] * f[v] + g[v] * f[u];
                //         ans += (m - 2) * g[u] * g[v];
                //     }
                
                for (int j = 0; j < m - 1; ++j) {
                    int v = scc[j];
                    g[u] += g[v];
                    f[u] += f[v] + (m - 1) * g[v];
                }
            }
        } else {
            low[u] = min(low[u], dfn[v]);
        }
    }
}

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1, u, v; i <= m; ++i) {
        scanf("%d%d", &u, &v);
        add(u, v), add(v, u);
    }
    for (int u = 1; u <= n; ++u)
        if (!dfn[u])
            tarjan(u, 0);
    printf("%lld", ans << 1);
    return 0;
}

类型二：维护点对间所有简单路径信息

先来看一道经典的问题。
例十二、必经点个数（洛谷，类似问题 UVA，类似问题 hydro-bzoj-3331 压力） Problem Statement

给你一张有 \(n\) 个点和 \(m\) 条边的无向图，有 \(q\) 次询问，给出点对 \((u,v)\)，求从 \(u\) 经过一条简单路径到 \(v\)，必须经过的节点数。

\(n,q\leq 5\times10^5\)，\(m\leq10^6\)。
Problem Analysis

放到圆方树上，均被包含的点，就是圆方树上路径上的圆点。这是因为对于非端点的一个圆点，它作为割点是必定会被经过的。于是可以简单求解。

时间复杂度 \(\mathcal{O}(m+n+q\log n)\)，尽管可以优化到完全线性。
Solution

#include <cstdio>
#include <iostream>
using namespace std;

const int N = 5e5 + 10;
const int M = 1e6 + 10;
const int lg2N = __lg(N << 1) + 1;

int n, m, q;

template <size_t _N, size_t _M>
class Graph {
public:
    Graph(): tot(1) {}
    struct node {
        int v, nxt;
    } edge[_M];
    int head[_N], tot;
    void add(int u, int v) {
        edge[++tot] = { v, head[u] };
        head[u] = tot;
    }
};

Graph<N, M << 1> G;
Graph<N << 1, N << 1> T;  // 圆方树

int dfn[N], low[N], timer;
int stack[N], top;

int dcc_cnt;
int pre[N << 1];

void tarjan(int u, int fr) {
    dfn[u] = low[u] = ++timer;
    stack[++top] = u;
    for (int i = G.head[u]; i; i = G.edge[i].nxt) {
        if (i == (fr ^ 1)) continue;
        int v = G.edge[i].v;
        if (!dfn[v]) {
            tarjan(v, i);
            low[u] = min(low[u], low[v]);
            if (low[v] >= dfn[u]) {
                ++dcc_cnt;
                T.add(u, dcc_cnt + n);
                while (true) {
                    int x = stack[top--];
                    T.add(dcc_cnt + n, x);
                    if (x == v) break;
                }
            }
        } else {
            low[u] = min(low[u], dfn[v]);
        }
    }
}

int fa[N << 1], dpt[N << 1];
int idx[N << 1], st[lg2N][N << 1];
void dfs(int u) {
    pre[u] = pre[fa[u]] + (u <= n);
    st[0][idx[u] = ++timer] = u;
    for (int i = T.head[u]; i; i = T.edge[i].nxt) {
        int v = T.edge[i].v;
        fa[v] = u;
        dpt[v] = dpt[u] + 1;
        dfs(v);
    }
}
inline int Min(int u, int v) {
    return dpt[u] < dpt[v] ? u : v;
}
inline int lca(int u, int v) {
    if (u == v) return u;
    if ((u = idx[u]) > (v = idx[v]))
        swap(u, v);
    int k = __lg(v - u++);
    return fa[Min(st[k][u], st[k][v - (1 << k) + 1])];
}
// O(n log n) ~ O(1) LCA

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1, u, v; i <= m; ++i) {
        scanf("%d%d", &u, &v);
        G.add(u, v), G.add(v, u);
    }
    tarjan(1, 0);
    timer = 0, dfs(1);
    for (int k = 1; k < lg2N; ++k)
        for (int i = 1; i + (1 << k) - 1 <= timer; ++i)
            st[k][i] = Min(st[k - 1][i], st[k - 1][i + (1 << (k - 1))]);
    scanf("%d", &q);
    for (int u, v; q--; ) {
        scanf("%d%d", &u, &v);
        int p = lca(u, v);
        int ans = pre[u] + pre[v] - pre[p] - pre[fa[p]];
        printf("%d\n", ans);
    }
    return 0;
}

接下来看一道典型的圆方树维护点对间所有简单路径信息的问题。
例十三、ZJOI2022 简单题（洛谷、UOJ） Problem Statement

一张 \(n\) 个点、\(m\) 条边的无重边无自环连通无向图，带有正整数边权。

一开始图上任意两个简单环的边权和相等。后来其中一部分边的权值改成了新的权值，因此，修改后的图可能没有这个性质。

现在给出修改后的图，同时给出多组询问，每次询问两点 \(S, T\) 间所有简单路径权值和对 \(998244353\) 取模的结果。

简单环和简单路径指不包含重复节点。

\(1 \le n, q \le 5 \times {10}^5\)，\(n - 1 \le m \le 6.4 \times {10}^5\)。
Problem Analysis

一道好题，关键在于分析出图的性质，否则无从下手。
这张图一开始任意两个简单环的边权和相等，这对这张图的形态做了限制，也就是说存在一种赋边权的方式，满足这个条件。

对于每一个点双考虑，因为简单环显然不会横跨两个点双，所以只会对点双内部的结构产生约束。接下来由简单到复杂，确定一个点双可能的形态。

1. 这个点双没有简单环。

   也即两个点被一条边连接的情况，显然合法。

2. 这个点双是一个简单环。

   显然合法。

3. 这个点双在一个简单环的基础上多了一条简单链。

   我们假设多出的一条链的两端是 \(S, T\)。那么他们之间就被三条简单路径连接。为了方便起见，我们把这三条链看做是连接 \(S, T\) 的三条边，边权对应简单链的边权和。

   

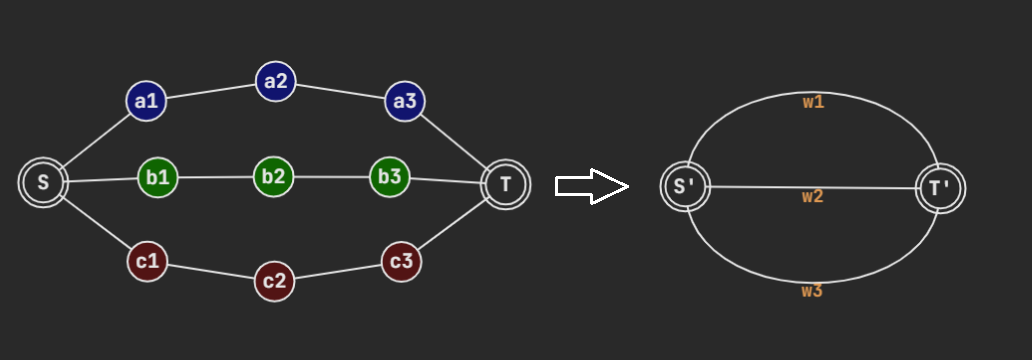
   我们只需要说明，存在一种给 \(w_1, w_2, w_3\) 赋权的方式，使得任意两个简单环的边权和相等。

   图上有三个简单环，设边权和分别为 \(s_1, s_2, s_3\)，有：

   \\\begin{cases} s_1=w_1+w_2 \\\\ s_2=w_1+w_3 \\\\ s_3=w_2+w_3 \\end{cases} \\

   只需令 \(w_1=w_2=w_3=k\)，其中 \(k\) 为任意正整数，就能使 \(s_1=s_2=s_3\)。

4. 这个点双在一个简单环的基础上，多了若干条以 \(S,T\) 为端点的简单链。

   类比 case 3 的推导，只需令 \(w_1=w_2=\cdots=w_t=k\)，其中 \(k\) 为任意正整数，就能使 \(s_1=s_2=\cdots=s_t\)。

5. 这个点双在一个简单环的基础上，多了两条不共端点的平行简单链。

   形如：

   

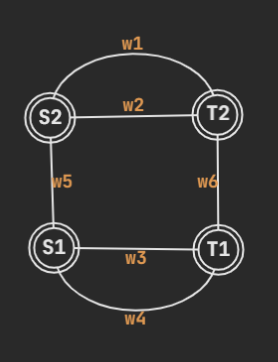
   类似地，这里存在六个环：

   \\\begin{cases} s_1=w_1+w_2 \\\\ s_2=w_3+w_4 \\\\ s_3=w_2+w_3+w_5+w_6 \\\\ s_4=w_2+w_3+w_5+w_6 \\\\ s_5=w_1+w_3+w_5+w_6 \\\\ s_6=w_2+w_4+w_5+w_6 \\\\ \\end{cases} \\

   令 \(w_1=w_2=w_3=w_4=w_5=w_6\)，看看能不能导出什么矛盾。手玩一会后发现，由 \(s_1+s_2=s_5+s_6\)，得到 \(w_5+w_6=0\)，而我们的边权都是正整数，所以这是不合法的。

   也就是说，一个点双的结构不可能是这样。有趣的是，如果我们令 \(w_5=w_6=0\)，那么这张图相当于退化成了 case 4 中 \(4\) 条链的情况，这似乎在暗示我们 case 4 或许就是我们要找的性质。

6. 这个点双在一个简单环的基础上，多了若干条不共端点的平行简单链。

   一定能得到类似 case 5 中的若干条等式，从而导出不可能。

7. 这个点双在一个简单环的基础上，多了两条不共端点的相交简单链。

   形如：

   

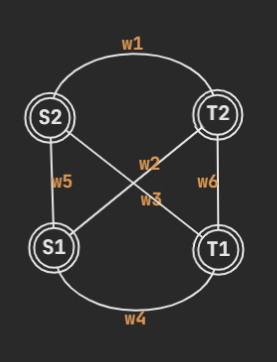
   这里同样存在六个环：

   \\\begin{cases} s_1=w_1+w_2+w_5 \\\\ s_2=w_1+w_3+w_6 \\\\ s_3=w_3+w_4+w_5 \\\\ s_4=w_2+w_4+w_6 \\\\ s_5=w_1+w_4+w_5+w_6 \\\\ s_6=w_2+w_3+w_5+w_6 \\\\ \\end{cases} \\

   类似根据 \(s_1+s_2=s_5+s_6\) 得到 \(w_6=0\)，根据对称性同样有 \(w_5=0\)，这也是不合法的，而且退化后的图也是 case 4 中 \(4\) 条链的情况。

8. 这个点双在一个简单环的基础上，多了若干条不共端点的相交简单链。

   一定能得到类似 case 7 中的若干条等式，从而导出不可能。

9. 这个点双在一个简单环的基础上，多了若干条不共端点的平行简单链，或相交简单链。

   一定能得到类似 case 5 或 case 7 中的若干条等式，从而导出不可能。

从而，我们证明了，只有 case 1、case 2、case 3、case 4 这几种点双的形态是合法的，进一步全部都可以归纳到 case 4 中：存在两个点 \(S,T\)，他们之间连了若干条简单链。\(1,2,3\) 条链分别退化到 case 1、case 2、case 3。

每个点双的形态就是确定的了：

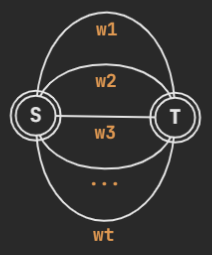
这种图似乎被称作「杏仁」，无论如何，这是一个关键的性质。

肯定需要上圆方树了。

根据经验，不难想到把 \((c,s)\) 这样的二元组作为所求信息，其中 \(c\) 表示简单路径条数，\(s\) 表示这些简单路径的边权总和。两个信息 \((c_1,s_1),(c_2,s_2)\) 合并后的结果即为 \((c_1c_2,c_1s_2+c_2s_1)\)。单位元即为 \((1,0)\)。

考虑 \(u\rightarrow v\) 的原子信息怎么求。记这个点双中 \(S,T\) 间有 \(c\) 条简单路径，边权和为 \(s\)，对于不为 \(S,T\) 的点 \(u\)，定义 \(\operatorname{from}(u)\) 表示 \(u\) 在 \(c\) 条简单路径中的哪一条上，\(\operatorname{disS}(u)\) 表示 \(S\) 通过 \(\operatorname{from}(u)\) 到 \(u\) 的距离，\(\operatorname{depthS}(u)\) 类似表示 \(S\) 通过 \(\operatorname{from}(u)\) 到 \(u\) 的边的条数，类似定义 \(\operatorname{disT}(u),\operatorname{depthT}(u)\)。接下来分类讨论。

1. \(u=S,v=T\)：

   信息即为 \((c,s)\)。

2. \(u=S,v\neq T\)：
   

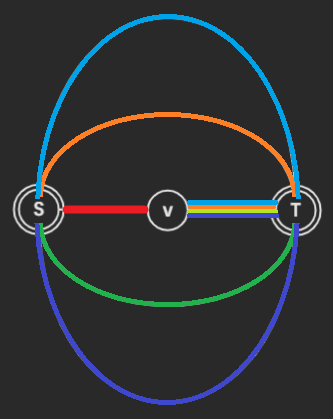
   信息为 \(\Big(c,s+\operatorname{disT}(v)\cdot(c-1-1)\Big)\)，\(c-1-1\) 表示 \(v\rightarrow T\) 这条边被 \(c-1\) 条路径经过，但是已经在 \(s\) 中贡献了一次，所以是 \(c-1-1\)。

3. \(u,v\not\in\{S,T\},\operatorname{from}(u)=\operatorname{from}(v),\operatorname{depthS}(u)\leq\operatorname{depthS}(v)\)：
   

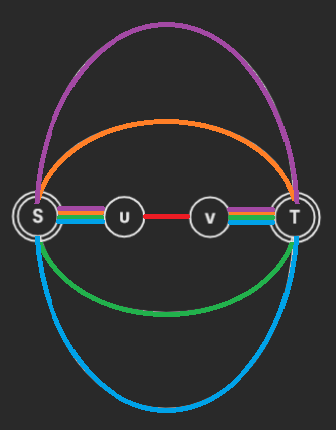
   信息为 \(\Big(c,s+(\operatorname{disT}(v)+\operatorname{disS}(u))\cdot(c-1-1)\Big)\)。

4. \(u,v\not\in\{S,T\},\operatorname{from}(u)\neq\operatorname{from}(v)\)：
   

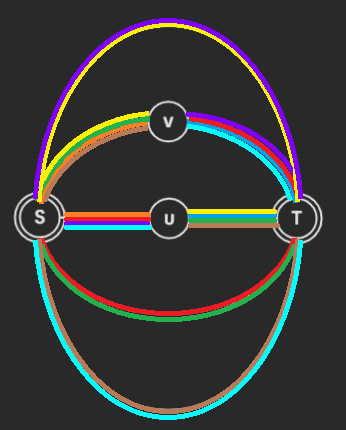
   信息为 \(\Big(2c-2, 2s + (\operatorname{disS}(u)+\operatorname{disT}(u))\cdot(c-1-2) + (\operatorname{disS}(v)+\operatorname{disT}(v))\cdot(c-1-2)\Big)\)。

剩下的情况都是对称的，此略去。

至于如何求出这些信息，只需要把点双的子图建出来，这就是前文仙人掌部分提到的弹边栈的方式，在弹出一条边的时候，在另一张图上加边。这另一张图就是这个点双的子图，根据度数找出 \(S,T\) 后，就可以方便处理出其他信息了。

于是我们可以套用圆方树多次询问点对信息的模式方便求解。

这个信息显然满足交换律，所以不需要考虑合并信息的顺序。

在了解圆方树后，这份代码实现起来并不困难。

时间复杂度 \(\mathcal{O}(m+n\log n+q\log n)\)。
Solution 圆方树

#include <cstdio>
#include <iostream>
using namespace std;

const int mod = 998244353;
const int N = 5e5 + 10;
const int M = 6.4e5 + 10;
const int N2 = N << 1;
const int lg2N = __lg(N2) + 1;

int n, m, q;

inline int add(int a, int b) {
    return a += b, a >= mod ? a - mod : a;
}
inline int mul(int a, int b) {
    return 1ll * a * b % mod;
}

struct node {
    int cnt, sum;
    friend node operator * (const node& a, const node& b) {
        return {
            mul(a.cnt, b.cnt),
            add(mul(b.cnt, a.sum), mul(a.cnt, b.sum))
        };
    }
};

template <size_t _N, size_t _M, typename T = int>
class Grpah {
public:
    Grpah(): tot(1) {}
    struct node {
        int v, nxt;
        T w;
    } edge[_M];
    int head[_N], tot;
    void add(int u, int v, const T& w) {
        edge[++tot] = { v, head[u], w };
        head[u] = tot;
    }
};
Grpah<N, M << 1> G;  // original grpah
Grpah<N << 1, N << 1, node> T;  // rebuild tree
Grpah<N, M << 1> SG;  // sub graph

int dfn[N], low[N], timer;
int est[N], etp;
int sccno[N], scc_cnt, scc_siz[N];
int _du[N], _scc[N], _siz;

int A[N], B[N];
int esum[N];
int pathCnt[N];
int from[N], dptS[N];
int disT[N], disS[N];

void getFromDisS(int x, int T, int fr) {
    for (int i = SG.head[x]; i; i = SG.edge[i].nxt) {
        int v = SG.edge[i].v;
        int w = SG.edge[i].w;
        if (v == fr || v == T) continue;
        disS[v] = add(disS[x], w);
        dptS[v] = dptS[x] + 1;
        from[v] = from[x];
        getFromDisS(v, T, x);
    }
}

void getDisT(int x, int S, int fr) {
    for (int i = SG.head[x]; i; i = SG.edge[i].nxt) {
        int v = SG.edge[i].v;
        int w = SG.edge[i].w;
        if (v == fr || v == S) continue;
        disT[v] = add(disT[x], w);
        getDisT(v, S, x);
    }
}

node getdis(int u, int v, int s) {
    if (u == v) return { 1, 0 };
    int frU = from[u], frV = from[v];
    int disSU = disS[u], disSV = disS[v];
    int disTU = disT[u], disTV = disT[v];
    int du = dptS[u], dv = dptS[v];
    int S = A[s], T = B[s];
    int sum = esum[s];
    int pcnt = pathCnt[s];
    if (u == S && v == T)
        return { pcnt, sum };
    if (v == S && u == T)
        return { pcnt, sum };
    if (u == S)
        return { pcnt, add(sum, mul(disTV, pcnt - 1 - 1)) };
    if (u == T)
        return { pcnt, add(sum, mul(disSV, pcnt - 1 - 1)) };
    if (v == S)
        return { pcnt, add(sum, mul(disTU, pcnt - 1 - 1)) };
    if (v == T)
        return { pcnt, add(sum, mul(disSU, pcnt - 1 - 1)) };
    if (frU == frV) {
        if (du < dv)
            return { pcnt, add(sum, mul(add(disSU, disTV), pcnt - 1 - 1)) };
        else
            return { pcnt, add(sum, mul(add(disSV, disTU), pcnt - 1 - 1)) };
    }
    return { (pcnt - 1) * 2, add(mul(sum, 2), add(mul(add(disSU, disTU), pcnt - 1 - 2), mul(add(disSV, disTV), pcnt - 1 - 2))) };
}

void deal(int p) {
    A[p] = B[p] = -1;
    for (int i = 0; i < _siz; ++i) {
        int u = _scc[i];
        if (_du[u] <= 2) continue;
        if (A[p] == -1)
            A[p] = u;
        else {
            B[p] = u;
            break;
        }
    }
    if (A[p] == -1)
        A[p] = _scc[0], B[p] = _scc[1];
    int S = A[p], T = B[p];
    disS[S] = 0;
    dptS[S] = 0;
    for (int i = SG.head[S]; i; i = SG.edge[i].nxt) {
        ++pathCnt[p];
        int v = SG.edge[i].v;
        int w = SG.edge[i].w;
        if (v == T) continue;
        dptS[v] = 1;
        disS[v] = w;
        from[v] = v;
        getFromDisS(v, T, S);
    }
    disT[T] = 0;
    getDisT(T, S, 0);
}

int _vis[N], _vis_tim;
void insert(int u) {
    if (_vis[u] == _vis_tim) return;
    _vis[u] = _vis_tim;
    _scc[_siz++] = u;
}

void tarjan(int u, int fr) {
    dfn[u] = low[u] = ++timer;
    for (int i = G.head[u]; i; i = G.edge[i].nxt) {
        if (i == (fr ^ 1)) continue;
        int v = G.edge[i].v;
        if (!dfn[v]) {
            est[++etp] = i;
            tarjan(v, i);
            low[u] = min(low[u], low[v]);
            if (low[v] >= dfn[u]) {
                ++scc_cnt, ++_vis_tim, _siz = 0;
                SG.tot = 1;
                while (true) {
                    int x = est[etp--];
                    int u = G.edge[x    ].v;
                    int v = G.edge[x ^ 1].v;
                    int w = G.edge[x    ].w;
                    insert(u), insert(v);
                    ++_du[u], ++_du[v];
                    esum[scc_cnt] = add(esum[scc_cnt], w);
                    SG.add(u, v, w);
                    SG.add(v, u, w);
                    if (x == i) break;
                }
                deal(scc_cnt);
                for (int i = 0; i < _siz; ++i) {
                    int x = _scc[i];
                    if (x == u) continue;
                    T.add(scc_cnt + n, x, getdis(u, x, scc_cnt));
                }
                T.add(u, scc_cnt + n, { 1, 0 });
                
                _du[u] = SG.head[u] = 0;
            }
        } else {
            low[u] = min(low[u], dfn[v]);
            if (dfn[v] < dfn[u])
                est[++etp] = i;
        }
    }
}

int fa[lg2N][N << 1], dpt[N << 1];
node val[lg2N][N << 1];

void dfs(int u) {
    for (int i = T.head[u]; i; i = T.edge[i].nxt) {
        int v = T.edge[i].v;
        fa[0][v] = u;
        val[0][v] = T.edge[i].w;
        dpt[v] = dpt[u] + 1;
        dfs(v);
    }
}

int query(int u, int v) {
    if (dpt[u] < dpt[v]) swap(u, v);
    node res = { 1, 0 };
    for (int i = lg2N - 1; ~i; --i)
        if (fa[i][u] && dpt[fa[i][u]] >= dpt[v]) {
            res = res * val[i][u];
            u = fa[i][u];
        }
    if (u == v) return res.sum;
    for (int i = lg2N - 1; ~i; --i)
        if (fa[i][u] != fa[i][v]) {
            res = res * val[i][u] * val[i][v];
            u = fa[i][u], v = fa[i][v];
        }
    if (fa[0][u] > n)
        res = res * getdis(u, v, fa[0][u] - n);
    else
        res = res * val[0][u] * val[0][v];  // this is not necessary
    return res.sum;
}

int main() {
#ifndef XuYueming
    // freopen("simple.in", "r", stdin);
    // freopen("simple.out", "w", stdout);
#endif
    scanf("%d%d%d", &n, &m, &q);
    for (int i = 1, u, v, w; i <= m; ++i) {
        scanf("%d%d%d", &u, &v, &w);
        G.add(u, v, w);
        G.add(v, u, w);
    }
    tarjan(1, 0);
    dfs(1);
    for (int k = 1; k < lg2N; ++k)
        for (int u = 1; u <= n + scc_cnt; ++u) {
            fa[k][u] = fa[k - 1][fa[k - 1][u]];
            if (fa[k][u])
                val[k][u] = val[k - 1][u] * val[k - 1][fa[k - 1][u]];
        }
    for (int u, v; q--; ) {
        scanf("%d%d", &u, &v);
        printf("%d\n", query(u, v));
    }
    return 0;
}

圆树

#include <cstdio>
#include <iostream>
using namespace std;

const int mod = 998244353;
const int N = 5e5 + 10;
const int M = 6.4e5 + 10;
const int lgN = __lg(N) + 1;

int n, m, q;

inline int add(int a, int b) {
    return a += b, a >= mod ? a - mod : a;
}
inline int mul(int a, int b) {
    return 1ll * a * b % mod;
}

struct node {
    int cnt, sum;
    friend node operator * (const node& a, const node& b) {
        return {
            mul(a.cnt, b.cnt),
            add(mul(b.cnt, a.sum), mul(a.cnt, b.sum))
        };
    }
};

template <size_t _N, size_t _M, typename T = int>
class Grpah {
public:
    Grpah(): tot(1) {}
    struct node {
        int v, nxt;
        T w;
    } edge[_M];
    int head[_N], tot;
    void add(int u, int v, const T& w) {
        edge[++tot] = { v, head[u], w };
        head[u] = tot;
    }
};
Grpah<N, M << 1> G;  // original grpah
Grpah<N, N, node> T;  // rebuild tree
Grpah<N, M << 1> SG;  // sub graph

int dfn[N], low[N], timer;
int est[N], etp;
int sccno[N], scc_cnt, scc_siz[N];
int _du[N], _scc[N], _siz;

int A[N], B[N];
int esum[N];
int pathCnt[N];
int from[N], dptS[N];
int disT[N], disS[N];

void getFromDisS(int x, int T, int fr) {
    for (int i = SG.head[x]; i; i = SG.edge[i].nxt) {
        int v = SG.edge[i].v;
        int w = SG.edge[i].w;
        if (v == fr || v == T) continue;
        disS[v] = add(disS[x], w);
        dptS[v] = dptS[x] + 1;
        from[v] = from[x];
        getFromDisS(v, T, x);
    }
}

void getDisT(int x, int S, int fr) {
    for (int i = SG.head[x]; i; i = SG.edge[i].nxt) {
        int v = SG.edge[i].v;
        int w = SG.edge[i].w;
        if (v == fr || v == S) continue;
        disT[v] = add(disT[x], w);
        getDisT(v, S, x);
    }
}

node getdis(int u, int v, int s) {
    if (u == v) return { 1, 0 };
    int frU = from[u], frV = from[v];
    int disSU = disS[u], disSV = disS[v];
    int disTU = disT[u], disTV = disT[v];
    int du = dptS[u], dv = dptS[v];
    int S = A[s], T = B[s];
    int sum = esum[s];
    int pcnt = pathCnt[s];
    if (u == S && v == T)
        return { pcnt, sum };
    if (v == S && u == T)
        return { pcnt, sum };
    if (u == S)
        return { pcnt, add(sum, mul(disTV, pcnt - 1 - 1)) };
    if (u == T)
        return { pcnt, add(sum, mul(disSV, pcnt - 1 - 1)) };
    if (v == S)
        return { pcnt, add(sum, mul(disTU, pcnt - 1 - 1)) };
    if (v == T)
        return { pcnt, add(sum, mul(disSU, pcnt - 1 - 1)) };
    if (frU == frV) {
        if (du < dv)
            return { pcnt, add(sum, mul(add(disSU, disTV), pcnt - 1 - 1)) };
        else
            return { pcnt, add(sum, mul(add(disSV, disTU), pcnt - 1 - 1)) };
    }
    return { (pcnt - 1) * 2, add(mul(sum, 2), add(mul(add(disSU, disTU), pcnt - 1 - 2), mul(add(disSV, disTV), pcnt - 1 - 2))) };
}

void deal(int p) {
    A[p] = B[p] = -1;
    for (int i = 0; i < _siz; ++i) {
        int u = _scc[i];
        if (_du[u] <= 2) continue;
        if (A[p] == -1)
            A[p] = u;
        else {
            B[p] = u;
            break;
        }
    }
    if (A[p] == -1)
        A[p] = _scc[0], B[p] = _scc[1];
    int S = A[p], T = B[p];
    disS[S] = 0;
    dptS[S] = 0;
    for (int i = SG.head[S]; i; i = SG.edge[i].nxt) {
        ++pathCnt[p];
        int v = SG.edge[i].v;
        int w = SG.edge[i].w;
        if (v == T) continue;
        dptS[v] = 1;
        disS[v] = w;
        from[v] = v;
        getFromDisS(v, T, S);
    }
    disT[T] = 0;
    getDisT(T, S, 0);
}

int _vis[N], _vis_tim;
void insert(int u) {
    if (_vis[u] == _vis_tim) return;
    _vis[u] = _vis_tim;
    _scc[_siz++] = u;
    sccno[u] = scc_cnt;
}

void tarjan(int u, int fr) {
    dfn[u] = low[u] = ++timer;
    for (int i = G.head[u]; i; i = G.edge[i].nxt) {
        if (i == (fr ^ 1)) continue;
        int v = G.edge[i].v;
        if (!dfn[v]) {
            est[++etp] = i;
            tarjan(v, i);
            low[u] = min(low[u], low[v]);
            if (low[v] >= dfn[u]) {
                ++scc_cnt, ++_vis_tim, _siz = 0;
                SG.tot = 1;
                while (true) {
                    int x = est[etp--];
                    int u = G.edge[x    ].v;
                    int v = G.edge[x ^ 1].v;
                    int w = G.edge[x    ].w;
                    insert(u), insert(v);
                    ++_du[u], ++_du[v];
                    esum[scc_cnt] = add(esum[scc_cnt], w);
                    SG.add(u, v, w);
                    SG.add(v, u, w);
                    if (x == i) break;
                }
                deal(scc_cnt);
                for (int i = 0; i < _siz; ++i) {
                    int x = _scc[i];
                    if (x == u) continue;
                    T.add(u, x, getdis(u, x, scc_cnt));
                }
                _du[u] = SG.head[u] = 0;
            }
        } else {
            low[u] = min(low[u], dfn[v]);
            if (dfn[v] < dfn[u])
                est[++etp] = i;
        }
    }
}

int fa[lgN][N], dpt[N];
node val[lgN][N];

void dfs(int u) {
    for (int i = T.head[u]; i; i = T.edge[i].nxt) {
        int v = T.edge[i].v;
        fa[0][v] = u;
        val[0][v] = T.edge[i].w;
        dpt[v] = dpt[u] + 1;
        dfs(v);
    }
}

int query(int u, int v) {
    if (dpt[u] < dpt[v]) swap(u, v);
    node res = { 1, 0 };
    for (int i = lgN - 1; ~i; --i)
        if (fa[i][u] && dpt[fa[i][u]] >= dpt[v]) {
            res = res * val[i][u];
            u = fa[i][u];
        }
    if (u == v) return res.sum;
    for (int i = lgN - 1; ~i; --i)
        if (fa[i][u] != fa[i][v]) {
            res = res * val[i][u] * val[i][v];
            u = fa[i][u], v = fa[i][v];
        }
    if (sccno[u] == sccno[v])
        res = res * getdis(u, v, sccno[u]);
    else
        res = res * val[0][u] * val[0][v];  // this is now necessary
    return res.sum;
}

int main() {
#ifndef XuYueming
    // freopen("simple.in", "r", stdin);
    // freopen("simple.out", "w", stdout);
#endif
    scanf("%d%d%d", &n, &m, &q);
    for (int i = 1, u, v, w; i <= m; ++i) {
        scanf("%d%d%d", &u, &v, &w);
        G.add(u, v, w);
        G.add(v, u, w);
    }
    tarjan(1, 0);
    dfs(1);
    for (int k = 1; k < lgN; ++k)
        for (int u = 1; u <= n; ++u) {
            fa[k][u] = fa[k - 1][fa[k - 1][u]];
            if (fa[k][u])
                val[k][u] = val[k - 1][u] * val[k - 1][fa[k - 1][u]];
        }
    for (int u, v; q--; ) {
        scanf("%d%d", &u, &v);
        printf("%d\n", query(u, v));
    }
    return 0;
}

接下来我们来看一道特殊的带修改的问题。
例十四、Tourists（Codeforces） Problem Statement

一张 \(n\) 个点、\(m\) 条边的连通无向图，带有点权。你需要支持：

1. 修改点权。
2. 询问 \(u,v\) 为端点的所有简单路径中，点权最小值的最小值。

\(1\leq n,m,q\leq 10^5\)。
Problem Analysis

方点在圆方树上的点权为，它的所有孩子圆点在原图上的点权的最小值。圆点的在圆方树上的点权为最小值的单位元，即 \(\infty\)。

给出树链剖分维护圆方树的实现方式。
Solution

#include <cstdio>
#include <iostream>
#include <set>
using namespace std;

const int N = 1e5 + 10;
const int M = 1e5 + 10;
const int NN = N << 1;
const int lg2N = __lg(NN) + 1;
const int inf = 0x3f3f3f3f;

int n, m, q, w[N];

template <size_t _N, size_t _M>
class Grpah {
public:
    Grpah(): tot(1) {}
    struct node {
        int v, nxt;
    } edge[_M];
    int head[_N], tot;
    void add(int u, int v) {
        edge[++tot] = { v, head[u] };
        head[u] = tot;
    }
};
Grpah<N, M << 1> G;  // original grpah
Grpah<N << 1, N << 1> T;  // rebuild tree

multiset<int> sss[N];  // 每个方点的数据结构
int scc_cnt;

namespace $build {

int dfn[N], low[N], timer;
int stack[N], top;

void tarjan(int u, int fr) {
    dfn[u] = low[u] = ++timer;
    stack[++top] = u;
    for (int i = G.head[u]; i; i = G.edge[i].nxt) {
        if (i == (fr ^ 1)) continue;
        int v = G.edge[i].v;
        if (!dfn[v]) {
            tarjan(v, i);
            low[u] = min(low[u], low[v]);
            if (low[v] >= dfn[u]) {
                ++scc_cnt;
                while (true) {
                    int x = stack[top--];
                    T.add(scc_cnt + n, x);
                    sss[scc_cnt].insert(w[x]);
                    if (x == v) break;
                }
                T.add(u, scc_cnt + n);
            }
        } else {
            low[u] = min(low[u], dfn[v]);
        }
    }
}

}

namespace TREE {

#define lson (idx << 1)
#define rson (idx << 1 | 1)

int mi[NN << 2];

void build(int idx, int l, int r) {
    mi[idx] = inf;
    if (l == r) return;
    int mid = (l + r) >> 1;
    build(lson, l, mid);
    build(rson, mid + 1, r);
}

void modify(int idx, int trl, int trr, int p, int v) {
    if (trl == trr) return mi[idx] = v, void();
    int mid = (trl + trr) >> 1;
    if (p <= mid) modify(lson, trl, mid, p, v);
    else modify(rson, mid + 1, trr, p, v);
    mi[idx] = min(mi[lson], mi[rson]);
}

int query(int idx, int trl, int trr, int l, int r) {
    if (l <= trl && trr <= r) return mi[idx];
    int mid = (trl + trr) >> 1;
    if (r <= mid) return query(lson, trl, mid, l, r);
    if (l >  mid) return query(rson, mid + 1, trr, l, r);
    return min(query(lson, trl, mid, l, r), query(rson, mid + 1, trr, l, r));
}

#undef lson
#undef rson

}

int siz[NN], son[NN], top[NN];
int fa[NN], dpt[NN];
int idx[NN], timer;

void dfs(int u) {
    siz[u] = 1;
    for (int i = T.head[u]; i; i = T.edge[i].nxt) {
        int v = T.edge[i].v;
        fa[v] = u;
        dpt[v] = dpt[u] + 1;
        dfs(v);
        siz[u] += siz[v];
        if (siz[v] > siz[son[u]])
            son[u] = v;
    }
}

void redfs(int u, int tp) {
    top[u] = tp;
    idx[u] = ++timer;
    if (u <= n)
        TREE::modify(1, 1, n + scc_cnt, idx[u], inf);  // 圆点设置为单位元
    else
        TREE::modify(1, 1, n + scc_cnt, idx[u], *sss[u - n].begin());
    if (son[u]) redfs(son[u], tp);
    for (int i = T.head[u]; i; i = T.edge[i].nxt) {
        int v = T.edge[i].v;
        if (v == son[u]) continue;
        redfs(v, v);
    }
}

int query(int u, int v) {
    int res = inf;
    while (top[u] != top[v]) {
        if (dpt[top[u]] < dpt[top[v]])
            swap(u, v);
        res = min(res, TREE::query(1, 1, n + scc_cnt, idx[top[u]], idx[u]));
        u = fa[top[u]];
    }
    if (dpt[u] > dpt[v])
        swap(u, v);
    res = min(res, TREE::query(1, 1, n + scc_cnt, idx[u], idx[v]));
    if (u <= n) {
        res = min(res, w[u]);
    } else {
        if (fa[u])
            res = min(res, w[fa[u]]);
    }
    return res;
}

void modify(int u, int ww) {
    if (fa[u]) {
        int x = fa[u] - n;
        sss[x].erase(sss[x].find(w[u]));
        sss[x].insert(ww);
        TREE::modify(1, 1, n + scc_cnt, idx[x + n], *sss[x].begin());
    }
    w[u] = ww;
}

int main() {
    scanf("%d%d%d", &n, &m, &q);
    for (int i = 1; i <= n; ++i)
        scanf("%d", &w[i]);
    for (int i = 1, u, v; i <= m; ++i) {
        scanf("%d%d", &u, &v);
        G.add(u, v);
        G.add(v, u);
    }
    $build::tarjan(1, 0);
    TREE::build(1, 1, n + scc_cnt);
    dfs(1), redfs(1, 1);
    for (int u, v; q--; ) {
        char op[2];
        scanf("%s%d%d", op, &u, &v);
        if (*op == 'C')
            modify(u, v);
        else
            printf("%d\n", query(u, v));
    }
    return 0;
}

类型三：求给定点集的整体信息

来看一道没有显式建出虚树，而是利用虚树结构解决的问题。
例十五、SDOI2018 战略游戏（洛谷） Problem Statement

一张 \(n\) 个点、\(m\) 条边的连通无向图。

\(q\) 此询问，每次给出一个点集 \(S\)。你可以选择一个不在 \(S\) 中的点，如果存在 \(S\) 中两个点，在不经过你选择的这个点的前提下，不能够到达对方，那么这个方案就是合法的。求你有多少种选点的方案。

\(2\leq n\leq10^5\)，\(n-1\leq m\leq2\times10^5\)，\(1\leq q\leq10^5\)，\(\sum|S|\leq2\times10^5\)。
Problem Analysis

圆方树上，如果存在一个圆点，删去它之后的若干个连通块中，如果至少有两个连通块中都有 \(S\) 中的点，那么不在同一个连通块里的点就不能够互相到达，这个圆点就是合法的。

显然需要建出圆方树的虚树。观察下图，为 \(\{2,7,10\}\) 对应的虚树：

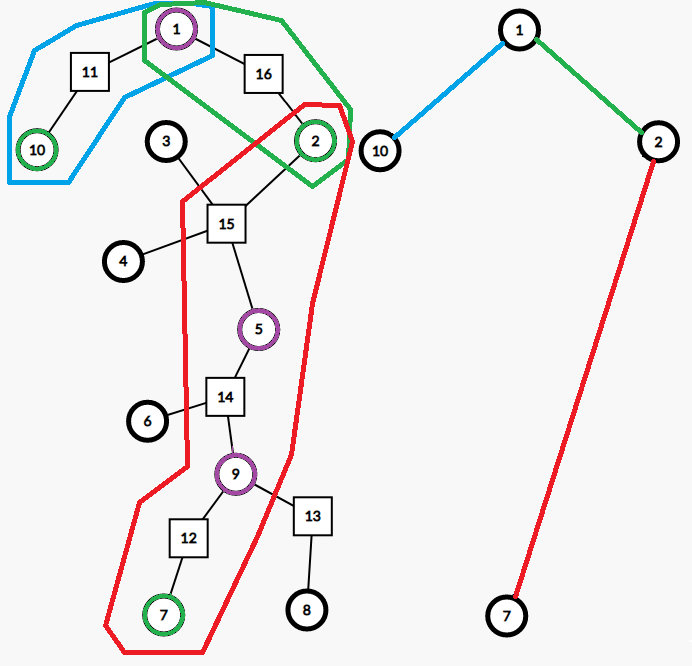
其中紫色圈出来的点表示贡献到答案里的点。我们不妨把 \(S\) 中的点先看做合法的，最后再减去他们。这样，我们就可以确定哪些圆点需要贡献到答案中去了。对于一条虚树上的树边 \((u,v)\)，圆方树上 \(u\rightarrow v\) 这条简单路径上的所有圆点都是合法的。正确性也十分显然。计数的话只需要做一遍树上前缀和就能单次 \(\mathcal{O}(1)\) 求出路径上有多少圆点。端点可能会重复统计？只需要在统计时，不统计父亲即可，因为父亲会恰好作为一次孩子被统计到，当然，除了根，那么最后看一下根是不是一个圆点即可。

时间复杂度 \(\mathcal{O}(m+n\log n+\sum|S|\log|S|)\)。

或者可以离线下来，配合 \(\mathcal{O}(n)\sim\mathcal{O}(1)\) LCA，做到 \(\mathcal{O}(|S|)\) 建立虚树，总的时间复杂度是线性 \(\mathcal{O}(m+n+\sum|S|)\)。
Solution

#include <cstdio>
#include <iostream>
#include <set>
#include <algorithm>
using namespace std;

const int N = 1e5 + 10;
const int M = 2e5 + 10;
const int NN = N << 1;
const int lg2N = __lg(NN) + 1;

int n, m, q;

template <size_t _N, size_t _M>
class Grpah {
public:
    Grpah(): tot(1) {}
    struct node {
        int v, nxt;
    } edge[_M];
    int head[_N], tot;
    void add(int u, int v) {
        edge[++tot] = { v, head[u] };
        head[u] = tot;
    }
};
Grpah<N, M << 1> G;  // original grpah
Grpah<N << 1, N << 1> T;  // rebuild tree

int scc_cnt;

namespace $build {

int dfn[N], low[N], timer;
int stack[N], top;

void tarjan(int u, int fr) {
    dfn[u] = low[u] = ++timer;
    stack[++top] = u;
    for (int i = G.head[u]; i; i = G.edge[i].nxt) {
        if (i == (fr ^ 1)) continue;
        int v = G.edge[i].v;
        if (!dfn[v]) {
            tarjan(v, i);
            low[u] = min(low[u], low[v]);
            if (low[v] >= dfn[u]) {
                ++scc_cnt;
                while (true) {
                    int x = stack[top--];
                    T.add(scc_cnt + n, x);
                    if (x == v) break;
                }
                T.add(u, scc_cnt + n);
            }
        } else {
            low[u] = min(low[u], dfn[v]);
        }
    }
}

}

int dpt[NN], fa[NN], timer;
int idx[NN], st[lg2N][NN];
int sum[NN];  // tree prefix sum, how many circle point

void dfs(int u) {
    st[0][idx[u] = ++timer] = u;
    for (int i = T.head[u]; i; i = T.edge[i].nxt) {
        int v = T.edge[i].v;
        dpt[v] = dpt[u] + 1;
        fa[v] = u;
        sum[v] = sum[u] + (v <= n);
        dfs(v);
    }
}
inline int Min(int a, int b) {
    return dpt[a] < dpt[b] ? a : b;
}
inline int lca(int u, int v) {
    if (u == v) return u;
    if ((u = idx[u]) > (v = idx[v])) swap(u, v);
    int k = __lg(v - u++);
    return fa[Min(st[k][u], st[k][v - (1 << k) + 1])];
}

void solve() {
    scanf("%d%d", &n, &m);
    for (int i = 1, u, v; i <= m; ++i) {
        scanf("%d%d", &u, &v);
        G.add(u, v);
        G.add(v, u);
    }
    $build::tarjan(1, 0);
    dfs(1);
    for (int k = 1; k < lg2N; ++k)
        for (int i = 1; i + (1 << k) - 1 <= n + scc_cnt; ++i)
            st[k][i] = Min(st[k - 1][i], st[k - 1][i + (1 << (k - 1))]);
    scanf("%d", &q);
    for (int i = 1, k; i <= q; ++i) {
        static int st[N << 1];
        scanf("%d", &k);
        for (int i = 1; i <= k; ++i)
            scanf("%d", &st[i]);
        sort(st + 1, st + k + 1, [] (int a, int b) {
            return idx[a] < idx[b];
        });
        for (int i = 1; i < k; ++i)
            st[k + i] = lca(st[i], st[i + 1]);
        sort(st + 1, st + k * 2, [] (int a, int b) {
            return idx[a] < idx[b];
        });
        int m = unique(st + 1, st + k * 2) - st - 1;
        int ans = 0;
        for (int i = 1; i < m; ++i) {
            int u = lca(st[i], st[i + 1]);
            int v = st[i + 1];
            ans += sum[v] - sum[u];
        }
        ans += st[1] <= n;
        ans -= k;
        printf("%d\n", ans);
    }
    for (int i = 1; i <= n; ++i) G.head[i] = 0, $build::dfn[i] = 0;
    for (int i = 1; i <= n + scc_cnt; ++i) T.head[i] = 0;
    G.tot = T.tot = 1;
    $build::top = $build::timer = 0;
    timer = scc_cnt = 0;
}

int main() {
    int t;
    scanf("%d", &t);
    while (t--) solve();
    return 0;
}

其他想讲的题目

例十五、同一点双？ Problem Statement

给你一个有 \(n\) 个点和 \(m\) 条边的无向图，和 \(q\) 组询问，每次询问两点 \(u,v\) 是否在同一点双内。

\(n\leq 10^5\)，\(m\leq 10^6\)，\(q\leq 10^6\)。
Problem Analysis

在经历了种种难题的洗礼，这一题就显得十分简单了。

两个点在同一个点双中，当且仅当存在一个连接他们的方点。

分类讨论可知，情况只有两种：其中一个是另一个的爷爷、其中一个是另一个的兄弟。前一种情况对应于一个是方点的父亲，一个是方点的孩子；后一种情况对应于两个都是方点的孩子。

于是每次可以 \(\mathcal{O}(1)\) 判断。

---

之所以有这一道水题，是因为《POI1999 Store-keeper 题解》中，本人采用「用来弹栈的割点」来理解此问题。事实上，在学习圆方树后，可以更清晰地理解这个问题：最终我们标记出来每个点所属的点双，和其在圆方树上的父亲是等价的。「用来弹栈的割点」便是方点的父亲圆点。

总结

通过本文的学习，我们深入探讨了圆方树这一结构在图论问题中的建模价值，特别是在仙人掌图及一般无向图中的实践应用。我们探究了树形 DP、点分治、树上启发式合并（DSU on tree）、树链剖分、虚树、动态 DP（DDP）、动态树等多种算法技巧，在这些图结构上的适用性和实现方法。同时，我们也厘清了一个核心问题：如何在这些图中高效维护点对之间所有简单路径的信息，从而为我们提供一种解决问题的全新的视角。

习题

这里总结了一些习题，大家可以练练手。

1. 例一、静态仙人掌最大独立集（小 C 的独立集，黑暗爆炸、洛谷、Hydro）
2. 例二、静态仙人掌直径（SHOI2008 仙人掌图，黑暗爆炸、洛谷、Hydro）
3. 例三、persistent DSU on cactus（洛谷）
4. 例四、GAME on cactus（洛谷）
5. 例五、仙人掌点对间最短路长度（【模板】静态仙人掌，洛谷）
6. 例六、BUY on cactus（洛谷）
7. 例七、【清华集训2015】静态仙人掌（UOJ）
8. 例八、mx 的仙人掌（UOJ）
9. 例九、【集训队互测2016】火车司机出秦川（UOJ）
10. 例十、DDP on cactus（洛谷）
11. 例十一、APIO2018 铁人两项（洛谷）
12. 例十二、必经点个数（洛谷，类似问题 UVA，类似问题 hydro-bzoj-3331 压力）
13. 例十三、ZJOI2022 简单题（洛谷、UOJ）
14. 例十四、Tourists（Codeforces）
15. 例十五、SDOI2018 战略游戏（洛谷）

欢迎补充。

编辑历史

• 2024-7-21：初版发布。
• 2025-3-19：开始重构。
• 2025-5-4：完成初稿。
• 2025-6-7：进一步整理重写，完成二稿。
• 2025-6-13：完成语言润色。
• 2025-7-19：学考后继续完善。新增仙人掌上换根 DP。
• 2025-7-19：检查审稿，发布终稿，投稿博客园首页。

原版博客

原版博客

前言

圆方树学习笔记，从一道例题讲起。

题目链接：Hydro & bzoj。

题意简述

仙人掌上求两点距离。

题目分析

为了把仙人掌的性质发挥出来，考虑将其变成一棵树。圆方树就是这样转换的工具。

先讲讲圆方树的概念：原图上的点为圆点，每个点双对应一个方点，树边都是方点连向点双内的圆点。

具体代码实现也十分简单，就是在 tarjan 求点双的时候，弹栈的时候，新建结点，并和点双内的点连边即可。或者在处理最后连边即可。

注意，对于孤立点的处理，是保持原样不动，还是变为一对方点和圆点，视情况讨论。以下代码按照上述定义，即对于孤立点，在圆方树上体现为一对方点和白点。

void tarjan(int now, int fa){
    dfn[now] = low[now] = ++timer, stack[++top] = now;
    int son = 0;
    for (int i = head[now]; i; i = edge[i].nxt){
        int to = edge[i].to;
        if (!dfn[to]){
            tarjan(to, now), low[now] = min(low[now], low[to]), ++son;
            if (low[to] >= dfn[now]){
                scc[++scc_cnt].push_back(now);
                do scc[scc_cnt].push_back(stack[top--]); while (stack[top + 1] != to);
            }
        } else if (to != fa) low[now] = min(low[now], dfn[to]);
    }
    if (!son && !fa) scc[++scc_cnt].push_back(now);
}
for (int i = 1; i <= scc_cnt; ++i)
    for (const auto& u: scc[i]) {
        yzh.add(i + n, u);
        yzh.add(u, i + n);
    }

void tarjan(int now, int fa){
    dfn[now] = low[now] = ++timer, stack[++top] = now;
    int son = 0;
    for (int i = head[now]; i; i = edge[i].nxt){
        int to = edge[i].to;
        if (!dfn[to]){
            tarjan(to, now), low[now] = min(low[now], low[to]), ++son;
            if (low[to] >= dfn[now]){
                ++scc_cnt;
                yzh.add(now, scc_cnt + n);
                yzh.add(scc_cnt + n, now);
                do {
                    int u = stack[top--];
                    yzh.add(u, scc_cnt + n);
                    yzh.add(scc_cnt + n, u);
                } while (stack[top + 1] != to);
            }
        } else if (to != fa) low[now] = min(low[now], dfn[to]);
    }
    if (!son && !fa) {
        ++scc_cnt;
        yzh.add(now, scc_cnt + n);
        yzh.add(scc_cnt + n, now);
    }
}

注意到，有时候，我们需要根据题意记录树边的边权。就比如例题。

思考我们建出树的意义是什么------原仙人掌上，不好求两点间的距离，而在树上，我们可以轻松利用 LCA 等方法求得两点间的距离。所以树的边权应该和距离有关。

我们发现，仙人掌中，原来的环都变成了菊花。原图上的距离是环上的最短距离，而在树上是从花瓣到花心，再从花心到花瓣。这样似乎没看出些什么。我们不妨把比较特殊的 LCA 处放在最后讨论，接下来只考虑往上跳 LCA 的过程。

发现，只会存在花瓣到花心，再到花顶端的那个花瓣。我们不妨设花心到顶端花瓣的距离为 \(0\)，而其余花瓣到花心的距离设置成原图环上到顶点的距离。这样就可以很好转化边权了。

至于 LCA 处，也很简单。如果 LCA 是圆点，那么不用处理；反之是方点，就要算其对应的原图上环的两点间的距离，这两点是来自询问两点不超过 LCA 的最浅祖先。这很好理解。

其实分析到这里，代码已经可以打出来了，但是在建树的时候注意如何优雅地处理边权，并精简代码。

那么再来模一模样例加深印象。

这里加粗的是原图的圆点，其他是方点。左图是圆仙人掌，右图是建出来的圆方树。

\(\operatorname{dist}(5, 7)\)：由于 \(\operatorname{LCA}(5, 7) = 1\) 是圆点，所以直接路径和相加，即 \(\operatorname{dist}(5, 7) = 3 + 0 + 1 + 0 + 2 + 0 = 6\)。

\(\operatorname{dist}(4, 8)\)：由于 \(\operatorname{LCA}(4, 8) = 14\) 是方点，所以要先跳到差一步到 \(14\) 的地方，即 \(4\) 和 \(3\)，环上距离为 \(\min \lbrace 1, 4 - 1 \rbrace = 1\)，\(\operatorname{dist}(4, 8) = 2 + 0 + 1 + 0 + 1 = 4\)。

代码

略去了快读快写，使用树剖求树上距离、LCA、和跳 father。

时间复杂度：\(\Theta(n + m + q \log n)\)，瓶颈在树剖查询的 \(\log\)。

#include <iostream>
#include <cstdio>
#include <vector>
using namespace std;

struct Graph{
    struct node{
        int to, nxt, len;
    } edge[1000010 << 1];
    int eid = 1, head[20010];
    inline void add(int u, int v, int w){
        edge[++eid] = {v, head[u], w};
        head[u] = eid;
    }
    inline node & operator [] (const int x){
        return edge[x];
    }
} xym, yzh;

int n, m, q;

int dfn[20010], low[20010], timer, cnt;
int dis[20010], re[20010];
int sum[20010], stack[20010], stop;
bool onleft[20010];

void tarjan(int now, int fr) {
    dfn[now] = low[now] = ++timer, stack[++stop] = now;
    for (int i = xym.head[now], to; to = xym[i].to, i; i = xym[i].nxt) if (i ^ fr ^ 1) {
        if (!dfn[to]) {
            dis[to] = dis[now] + xym[i].len;
            re[to] = xym[i].len;  // 如果这是一条非环边，那么把它看做 now -> to -> now 的环，所以这里要设置初值
            tarjan(to, i), low[now] = min(low[now], low[to]);
            if (low[to] >= dfn[now]) {
                ++cnt, sum[cnt] = re[stack[stop]] + dis[stack[stop]] - dis[now];  // 记录环的总长
                yzh.add(cnt, now, 0), yzh.add(now, cnt, 0);
                do {
                    int u = stack[stop--];
                    int len = min(dis[u] - dis[now], sum[cnt] - dis[u] + dis[now]);
                    onleft[u] = len == dis[u] - dis[now];
                    yzh.add(u, cnt, len);
                    yzh.add(cnt, u, len);
                } while (stack[stop + 1] != to);
            }
        } else if (dfn[to] < dfn[now]) {
            re[now] = xym[i].len;  // 环的闭环那条边的长度
            low[now] = min(low[now], dfn[to]);
        }
    }
}

int siz[20010], top[20010], son[20010];
int line[20010], tfa[20010], dpt[20010];

void dfs(int now, int fa) {
    tfa[now] = fa, siz[now] = 1, dpt[now] = dpt[fa] + 1;
    for (int i = yzh.head[now], to; to = yzh[i].to, i; i = yzh[i].nxt) {
        if (to == fa) continue;
        dis[to] = dis[now] + yzh[i].len;
        dfs(to, now), siz[now] += siz[to];
        if (siz[to] > siz[son[now]]) son[now] = to;
    }
}

void redfs(int now, int tp) {
    line[dfn[now] = ++timer] = now;
    top[now] = tp;
    if (son[now]) redfs(son[now], tp);
    for (int i = yzh.head[now], to; to = yzh[i].to, i; i = yzh[i].nxt) {
        if (to == tfa[now]) continue;
        if (to == son[now]) continue;
        redfs(to, to);
    }
}

inline int lca(int u, int v) {
    while (top[u] != top[v]) {
        if (dpt[top[u]] < dpt[top[v]]) swap(u, v);
        u = tfa[top[u]];
    }
    if (dpt[u] < dpt[v]) swap(u, v);
    return v;
}

inline int jump(int now, int ed) {
    int res = 0;
    while (top[now] != top[ed])
        res = top[now], now = tfa[top[now]];
    return now == ed ? res : line[dfn[ed] + 1];
}

inline int query(int u, int v) {
    int p = lca(u, v);
    if (p <= n)
        return dis[u] + dis[v] - 2 * dis[p];
    int fu = jump(u, p), fv = jump(v, p);
    int d1 = dis[fu] - dis[p], d2 = dis[fv] - dis[p];
    if (!onleft[fu]) d1 = sum[p] - d1;
    if (!onleft[fv]) d2 = sum[p] - d2;
    return dis[u] - dis[fu] + dis[v] - dis[fv] + min(abs(d1 - d2), sum[p] - abs(d1 - d2));
}

signed main() {
    fread(buf, 1, MAX, stdin);
    read(n), read(m), read(q);
    for (int i = 1, u, v, w; i <= m; ++i) {
        read(u), read(v), read(w);
        xym.add(u, v, w);
        xym.add(v, u, w);
    }
    cnt = n;
    for (int i = 1; i <= n; ++i) if (!dfn[i]) tarjan(i, 0);
    timer = dis[1] = 0, dfs(1, 0), redfs(1, 1);
    for (int i = 1, u, v; i <= q; ++i) {
        read(u), read(v);
        write(query(u, v)), putchar('\n');
    }
    fwrite(obuf, 1, o - obuf, stdout);
    return 0;
}

后记

不用圆方树亦可解此题，但是要多一些讨论、不如圆方树的直观。据说圆方树能在一般无向图上使用？我太蒻了啊。

// run
sidebarToggle();
window.cancelDetailsAnimation = true;