OpenCV 官翻 4 - 相机标定与三维重建

伊织code2025-07-20 20:04

文章目录

相机标定

https://docs.opencv.org/4.x/dc/dbb/tutorial_py_calibration.html

目标

在本节中，我们将学习以下内容：

  • 由相机引起的畸变类型
  • 如何找到相机的内参和外参属性
  • 如何基于这些属性对图像进行去畸变处理

基础原理

某些针孔相机会对图像引入明显的畸变。主要有两种畸变类型：径向畸变和切向畸变。

径向畸变会导致直线在图像中呈现弯曲。距离图像中心越远的点，径向畸变效应越显著。例如下图展示了一个标有红线的棋盘两边缘，但可以看到棋盘边框并非直线且与红线不重合，所有本应笔直的线条都出现了外凸现象。更多细节可参考光学畸变。

后续章节将引入若干新参数，详见相机标定与三维重建。

径向畸变的数学模型如下：

\[x_{畸变} = x( 1 + k_1 r^2 + k_2 r^4 + k_3 r^6) \\

y_{畸变} = y( 1 + k_1 r^2 + k_2 r^4 + k_3 r^6)\]

切向畸变则是由于镜头与成像平面不完全平行所导致，使得图像某些区域看起来比实际更近。其数学模型为：

\[x_{畸变} = x + [ 2p_1xy + p_2(r2+2x2)] \\

y_{畸变} = y + [ p_1(r^2+ 2y^2)+ 2p_2xy]\]

简而言之，我们需要求解五个畸变系数：

\[畸变系数=(k_1 \hspace{10pt} k_2 \hspace{10pt} p_1 \hspace{10pt} p_2 \hspace{10pt} k_3)\]

此外还需获取相机的内参和外参。内参是相机特有参数，包括焦距(\(f_x,f_y\))和光心坐标(\(c_x, c_y\))。这些参数可构成相机矩阵用于消除镜头畸变，该矩阵对于特定相机具有唯一性，计算后可重复用于同相机拍摄的其他图像。其3x3矩阵形式为：

\[相机矩阵 = \left [ \begin{matrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{matrix} \right ]\]

外参则对应旋转和平移向量，用于将三维点坐标转换到特定坐标系。

在立体视觉应用中，需先校正这些畸变。为求解参数，需要提供已知图案的样本图像（如棋盘格）。通过识别图案中已知相对位置的特定点（如棋盘角点），结合这些点在现实空间和图像中的坐标，即可解算畸变系数。为获得理想结果，至少需要10组测试图案。

代码

如前所述，我们至少需要10个测试图案来进行相机标定。OpenCV自带了一些棋盘格图像（参见 samples/data/left01.jpg -- left14.jpg），因此我们将使用这些图像。以一张棋盘格图像为例，相机标定所需的关键输入数据是：一组3D真实世界点坐标及其在图像中对应的2D坐标点。我们可以轻松从图像中获取2D图像点（这些图像点是棋盘格中两个黑色方块相接的位置）。

那么真实世界空间中的3D点如何确定呢？这些图像是由固定相机拍摄的，棋盘格被放置在不同位置和方向。因此我们需要知道\((X,Y,Z))坐标值。但为了简化，我们可以假设棋盘格始终保持在XY平面（即Z恒为0），相机则相应移动。这种设定让我们只需找出X,Y值。对于X,Y值，我们可以简单地传递(0,0)、(1,0)、(2,0)等点坐标来表示位置。这种情况下，得到的结果将以棋盘格方块的尺寸为比例单位。但如果我们知道方块的实际尺寸（比如30毫米），就可以传递(0,0)、(30,0)、(60,0)等值，这样结果将以毫米为单位（本例中由于我们未实际测量那些图像的方块尺寸，所以使用方块尺寸作为单位）。

3D点被称为对象点 ，2D图像点则称为图像点。

配置

要在棋盘上寻找图案，我们可以使用函数 cv.findChessboardCorners()。我们还需要指定要寻找的图案类型，例如8x8网格、5x5网格等。本例中我们使用7x6网格（通常棋盘有8x8个方格和7x7个内部角点）。该函数会返回角点坐标和一个布尔值retval------若成功检测到图案则返回True。这些角点会按特定顺序排列（从左到右，从上到下）。

注意：此函数可能无法在所有图像中找到目标图案。因此，较好的做法是编写代码启动摄像头并逐帧检测目标图案。一旦检测到图案，就计算角点坐标并存入列表。同时，在读取下一帧前设置适当间隔，以便调整棋盘方向。重复此过程直至获得足够数量的有效图案。例如本文提供的14张样本图像中，我们也不确定有多少是有效的，因此需要全部读取并筛选出有效图像。

除了棋盘，我们也可以使用圆形网格。此时需改用 cv.findCirclesGrid() 函数来检测图案。使用圆形网格进行相机校准时，所需图像数量更少。

检测到角点后，可通过 cv.cornerSubPix() 提高其精度。还可以用 cv.drawChessboardCorners() 可视化图案。以下代码包含了上述所有步骤：

python 复制代码 
import numpy as np
import cv2 as cv
import glob

# termination criteria
criteria = (cv.TERM_CRITERIA_EPS + cv.TERM_CRITERIA_MAX_ITER, 30, 0.001)

# prepare object points, like (0,0,0), (1,0,0), (2,0,0) ....,(6,5,0)
objp = np.zeros((6*7,3), np.float32)
objp[:,:2] = np.mgrid[0:7,0:6].T.reshape(-1,2)

# Arrays to store object points and image points from all the images.
objpoints = [] # 3d point in real world space
imgpoints = [] # 2d points in image plane.

images = glob.glob('*.jpg')

for fname in images:
    img = cv.imread(fname)
    gray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)

    # Find the chess board corners
    ret, corners = cv.findChessboardCorners(gray, (7,6), None)

    # If found, add object points, image points (after refining them)
    if ret == True:
        objpoints.append(objp)

        corners2 = cv.cornerSubPix(gray,corners, (11,11), (-1,-1), criteria)
        imgpoints.append(corners2)

        # Draw and display the corners
        cv.drawChessboardCorners(img, (7,6), corners2, ret)
        cv.imshow('img', img)
        cv.waitKey(500)

cv.destroyAllWindows()

一张绘有图案的图片如下所示：

校准

现在我们已经获得了物体点和图像点，可以进行校准了。我们可以使用函数 cv.calibrateCamera()，该函数会返回相机矩阵、畸变系数、旋转和平移向量等参数。

python 复制代码 
ret, mtx, dist, rvecs, tvecs = cv.calibrateCamera(objpoints, imgpoints, gray.shape[::-1], None, None)

去畸变

现在我们可以对图像进行去畸变处理。OpenCV提供了两种方法来实现这一功能。但首先，我们可以基于自由缩放参数使用**cv.getOptimalNewCameraMatrix()**来优化相机矩阵。如果缩放参数alpha=0，函数会返回去除最多无用像素的去畸变图像，甚至可能裁切掉图像角落的部分像素。若alpha=1，则保留所有像素并在图像边缘添加黑色区域。该函数还会返回一个图像ROI区域，可用于裁剪最终结果。

这里我们以新图像为例（本章第一个图像left12.jpg）

复制代码 
img = cv.imread('left12.jpg')
h,  w = img.shape[:2]
newcameramtx, roi = cv.getOptimalNewCameraMatrix(mtx, dist, (w,h), 1, (w,h))

1、使用 cv.undistort()

这是最简单的方法。只需调用该函数，并使用之前获取的ROI对结果进行裁剪。

python 复制代码 
# undistort
dst = cv.undistort(img, mtx, dist, None, newcameramtx)

# crop the image
x, y, w, h = roi
dst = dst[y:y+h, x:x+w]
cv.imwrite('calibresult.png', dst)

2、使用重映射方法

这种方式稍复杂一些。首先需要找到一个从畸变图像到无畸变图像的映射函数，然后使用remap函数进行处理。

python 复制代码 
# undistort
mapx, mapy = cv.initUndistortRectifyMap(mtx, dist, None, newcameramtx, (w,h), 5)
dst = cv.remap(img, mapx, mapy, cv.INTER_LINEAR)

# crop the image
x, y, w, h = roi
dst = dst[y:y+h, x:x+w]
cv.imwrite('calibresult.png', dst)

不过，这两种方法得出的结果相同。查看下方结果：

从结果中可以看到所有边缘都保持笔直。

现在，你可以使用NumPy的写入函数（如np.savez、np.savetxt等）存储相机矩阵和畸变系数，以便后续使用。

重投影误差

重投影误差能有效评估所找到参数的精确程度。该误差值越接近零，表示我们获得的参数越准确。在已知内参矩阵、畸变系数、旋转矩阵和平移矩阵的情况下，我们需要先使用 cv.projectPoints() 将物体点转换为图像点。然后，可以计算通过该变换得到的点与角点检测算法找到的点之间的绝对范数。要计算平均误差，需对所有标定图像计算得到的误差取算术平均值。

python 复制代码 
mean_error = 0
for i in range(len(objpoints)):
    imgpoints2, _ = cv.projectPoints(objpoints[i], rvecs[i], tvecs[i], mtx, dist)
    error = cv.norm(imgpoints[i], imgpoints2, cv.NORM_L2)/len(imgpoints2)
    mean_error += error

print( "total error: {}".format(mean_error/len(objpoints)) )

练习

1、尝试使用圆形网格进行相机标定。

本文档由 doxygen 1.12.0 生成于 2025年4月30日 星期三 23:08:42，针对 OpenCV 项目

姿态估计

https://docs.opencv.org/4.x/d7/d53/tutorial_py_pose.html

目标

在本节中，

  • 我们将学习利用 calib3d 模块在图像中创建一些 3D 效果。

基础

这部分内容会比较简短。在上次关于相机校准的课程中，你已经获取了相机矩阵、畸变系数等参数。给定一个标定板图像，我们可以利用这些信息来计算其姿态（即物体在空间中的位置和方向），例如物体的旋转角度、位移情况等。对于平面物体，我们可以假设Z=0，这样问题就转化为：相机在空间中如何摆放才能观测到我们的标定板图像。因此，如果我们知道物体在空间中的位置，就可以绘制一些2D图形来模拟3D效果。下面我们来看看具体实现方法。

我们的目标是：在棋盘格的第一个角点绘制3D坐标轴（X、Y、Z轴），其中X轴用蓝色表示，Y轴用绿色表示，Z轴用红色表示。最终效果中，Z轴应该看起来垂直于棋盘格平面。

首先，我们需要从之前的校准结果中加载相机矩阵和畸变系数。

python 复制代码 
import numpy as np
import cv2 as cv
import glob

# Load previously saved data
with np.load('B.npz') as X:
    mtx, dist, _, _ = [X[i] for i in ('mtx','dist','rvecs','tvecs')]

现在我们来创建一个函数 draw，它接收棋盘角点（通过 cv.findChessboardCorners() 获取）和 坐标轴点 作为参数，用于绘制3D坐标轴。

python 复制代码 
def draw(img, corners, imgpts):
    corner = tuple(corners[0].ravel().astype("int32"))
    imgpts = imgpts.astype("int32")
    img = cv.line(img, corner, tuple(imgpts[0].ravel()), (255,0,0), 5)
    img = cv.line(img, corner, tuple(imgpts[1].ravel()), (0,255,0), 5)
    img = cv.line(img, corner, tuple(imgpts[2].ravel()), (0,0,255), 5)
    return img

与之前的情况类似，我们创建终止条件、对象点（棋盘角点的3D坐标）和轴点。轴点是用于绘制坐标轴的3D空间点。我们绘制长度为3的坐标轴（单位将基于棋盘方格尺寸，因为校准时使用了该尺寸）。因此，X轴从(0,0,0)绘制到(3,0,0)，Y轴同理。Z轴则从(0,0,0)绘制到(0,0,-3)，负号表示该轴向相机方向延伸。

python 复制代码 
criteria = (cv.TERM_CRITERIA_EPS + cv.TERM_CRITERIA_MAX_ITER, 30, 0.001)
objp = np.zeros((6*7,3), np.float32)
objp[:,:2] = np.mgrid[0:7,0:6].T.reshape(-1,2)

axis = np.float32([[3,0,0], [0,3,0], [0,0,-3]]).reshape(-1,3)

按照惯例，我们首先加载每张图像。搜索7x6的网格，如果找到，就用亚角点像素进行细化。接着，为了计算旋转和平移矩阵，我们调用函数 cv.solvePnPRansac()。得到这些变换矩阵后，我们将其用于将坐标轴点投影到图像平面。简而言之，就是找到3D空间中(3,0,0)、(0,3,0)、(0,0,3)各点在图像平面对应的位置。获取这些点后，通过generateImage()函数从第一个角点向这些点绘制连线。搞定！

python 复制代码 
for fname in glob.glob('left*.jpg'):
    img = cv.imread(fname)
    gray = cv.cvtColor(img,cv.COLOR_BGR2GRAY)
    ret, corners = cv.findChessboardCorners(gray, (7,6),None)

    if ret == True:
        corners2 = cv.cornerSubPix(gray,corners,(11,11),(-1,-1),criteria)

        # Find the rotation and translation vectors.
        ret,rvecs, tvecs = cv.solvePnP(objp, corners2, mtx, dist)

        # project 3D points to image plane
        imgpts, jac = cv.projectPoints(axis, rvecs, tvecs, mtx, dist)

        img = draw(img,corners2,imgpts)
        cv.imshow('img',img)
        k = cv.waitKey(0) & 0xFF
        if k == ord('s'):
            cv.imwrite(fname[:6]+'.png', img)

cv.destroyAllWindows()

以下是部分结果展示。请注意，每个坐标轴的长度为3个方格：

渲染立方体

如需绘制立方体，请按以下方式修改 generateImage() 函数及坐标点。

修改后的 generateImage() 函数：

python 复制代码 
def draw(img, corners, imgpts):
    imgpts = np.int32(imgpts).reshape(-1,2)

    # draw ground floor in green
    img = cv.drawContours(img, [imgpts[:4]],-1,(0,255,0),-3)

    # draw pillars in blue color
    for i,j in zip(range(4),range(4,8)):
        img = cv.line(img, tuple(imgpts[i]), tuple(imgpts[j]),(255),3)

    # draw top layer in red color
    img = cv.drawContours(img, [imgpts[4:]],-1,(0,0,255),3)

    return img

修改后的坐标轴点。它们是三维空间中立方体的8个角点：

python 复制代码 
axis = np.float32([[0,0,0], [0,3,0], [3,3,0], [3,0,0],
                   [0,0,-3],[0,3,-3],[3,3,-3],[3,0,-3] ])

看看下面的结果：

如果你对图形学、增强现实等领域感兴趣，可以使用OpenGL来渲染更复杂的图形。

生成于2025年4月30日星期三 23:08:42，由doxygen 1.12.0为OpenCV生成

极线几何

https://docs.opencv.org/4.x/da/de9/tutorial_py_epipolar_geometry.html

目标

在本节中，

  • 我们将学习多视图几何的基础知识
  • 我们将了解什么是极点（epipole）、极线（epipolar lines）、极线约束（epipolar constraint）等概念

基础概念

当我们使用针孔相机拍摄图像时，会丢失一个重要信息------图像的深度。由于这是从3D到2D的转换，我们无法知道图像中每个点距离相机有多远。因此，能否利用这些相机获取深度信息成为一个关键问题。解决方案就是使用多个相机。人类视觉系统采用类似原理，通过双目（两只眼睛）实现立体视觉。下面我们来看看OpenCV在这方面提供的功能。

（Gary Bradsky所著的《Learning OpenCV》包含该领域的丰富信息。）

在探讨深度图像之前，我们先了解多视图几何中的一些基础概念。本节将重点介绍极线几何。观察下图展示的双相机拍摄同一场景的基本配置：

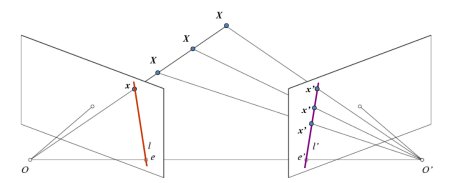
如果仅使用左相机，我们无法确定图像中点\(x\)对应的3D空间点，因为直线\(OX\)上的所有点在成像平面上都会投影到同一位置。但若同时考虑右相机图像，此时直线\(OX\)上的不同点会在右平面投影为不同位置（\(x'\)）。通过这两幅图像，我们就能三角测量出正确的3D点坐标，这就是核心原理。

在右平面上，\(OX\)直线上不同点的投影会形成一条直线（\(l'\)），我们称之为点\(x\)对应的极线 。这意味着要在右图像中寻找点\(x\)，只需沿这条极线搜索即可（设想一下：要在另一幅图像中寻找匹配点，无需搜索整个图像，只需沿极线搜索即可。这种方式能提高性能和精度）。这个原理称为极线约束 。同理，所有点在另一幅图像中都有对应的极线。平面\(XOO'\)被称为极平面。

\(O\)和\(O'\)分别代表两个相机的光心。从图示配置可以看出，右相机\(O'\)的投影会出现在左图像的\(e\)点处，这个点称为极点。极点是连接两个相机光心的直线与成像平面的交点。同理，\(e'\)是左相机的极点。某些情况下，极点可能位于图像外部（即一个相机无法看到另一个相机）。

所有极线都会通过其对应的极点。因此要确定极点位置，可以通过多条极线的交点来实现。

本节重点在于寻找极线和极点。但在此之前，我们还需要两个关键要素：基础矩阵(F)和本质矩阵(E)。本质矩阵包含平移和旋转信息，用于描述第二个相机相对于第一个相机在全局坐标系中的位置。见下图（图片来源：Gary Bradsky《Learning OpenCV》）：

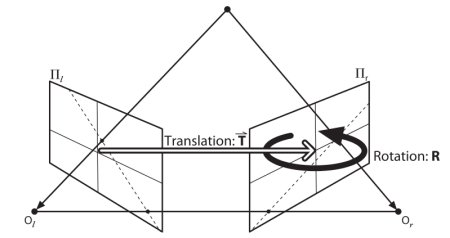
但实际测量通常采用像素坐标，对吧？基础矩阵不仅包含与本质矩阵相同的信息，还包含两个相机的内参信息，因此可以在像素坐标系中建立两个相机的关联（如果使用校正后的图像并通过焦距归一化点坐标，则\(F=E\)）。简而言之，基础矩阵F能将一个图像中的点映射到另一个图像中的极线上。该矩阵通过两幅图像的匹配点计算得出，使用8点算法时至少需要8对匹配点。建议使用更多匹配点并结合RANSAC算法以获得更稳健的结果。

代码

首先，我们需要在两幅图像之间找到尽可能多的匹配点，以计算基础矩阵。为此，我们使用基于FLANN匹配器的SIFT描述符，并采用比率测试方法。

python 复制代码 
import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt

img1 = cv.imread('myleft.jpg', cv.IMREAD_GRAYSCALE)  #queryimage # left image
img2 = cv.imread('myright.jpg', cv.IMREAD_GRAYSCALE) #trainimage # right image

sift = cv.SIFT_create()

# find the keypoints and descriptors with SIFT
kp1, des1 = sift.detectAndCompute(img1,None)
kp2, des2 = sift.detectAndCompute(img2,None)

# FLANN parameters
FLANN_INDEX_KDTREE = 1
index_params = dict(algorithm = FLANN_INDEX_KDTREE, trees = 5)
search_params = dict(checks=50)

flann = cv.FlannBasedMatcher(index_params,search_params)
matches = flann.knnMatch(des1,des2,k=2)

pts1 = []
pts2 = []

# ratio test as per Lowe's paper
for i,(m,n) in enumerate(matches):
    if m.distance < 0.8*n.distance:
        pts2.append(kp2[m.trainIdx].pt)
        pts1.append(kp1[m.queryIdx].pt)

现在我们得到了两幅图像的最佳匹配点列表。接下来计算基础矩阵(Fundamental Matrix)。

python 复制代码 
def drawlines(img1,img2,lines,pts1,pts2):
    ''' img1 - image on which we draw the epilines for the points in img2
        lines - corresponding epilines '''
    r,c = img1.shape
    img1 = cv.cvtColor(img1,cv.COLOR_GRAY2BGR)
    img2 = cv.cvtColor(img2,cv.COLOR_GRAY2BGR)
    for r,pt1,pt2 in zip(lines,pts1,pts2):
        color = tuple(np.random.randint(0,255,3).tolist())
        x0,y0 = map(int, [0, -r[2]/r[1] ])
        x1,y1 = map(int, [c, -(r[2]+r[0]*c)/r[1] ])
        img1 = cv.line(img1, (x0,y0), (x1,y1), color,1)
        img1 = cv.circle(img1,tuple(pt1),5,color,-1)
        img2 = cv.circle(img2,tuple(pt2),5,color,-1)
    return img1,img2

接下来我们寻找极线。在第一幅图像中点的对应极线会被绘制在第二幅图像上，因此这里正确指定图像非常重要。我们会得到一个线条数组，为此我们定义一个新函数来在图像上绘制这些线条。

python 复制代码 
def drawlines(img1,img2,lines,pts1,pts2):
    ''' img1 - image on which we draw the epilines for the points in img2
        lines - corresponding epilines '''
    r,c = img1.shape
    img1 = cv.cvtColor(img1,cv.COLOR_GRAY2BGR)
    img2 = cv.cvtColor(img2,cv.COLOR_GRAY2BGR)
    for r,pt1,pt2 in zip(lines,pts1,pts2):
        color = tuple(np.random.randint(0,255,3).tolist())
        x0,y0 = map(int, [0, -r[2]/r[1] ])
        x1,y1 = map(int, [c, -(r[2]+r[0]*c)/r[1] ])
        img1 = cv.line(img1, (x0,y0), (x1,y1), color,1)
        img1 = cv.circle(img1,tuple(pt1),5,color,-1)
        img2 = cv.circle(img2,tuple(pt2),5,color,-1)
    return img1,img2

现在我们在两张图像中找到并绘制对极线。

python 复制代码 
# Find epilines corresponding to points in right image (second image) and
# drawing its lines on left image
lines1 = cv.computeCorrespondEpilines(pts2.reshape(-1,1,2), 2,F)
lines1 = lines1.reshape(-1,3)
img5,img6 = drawlines(img1,img2,lines1,pts1,pts2)

# Find epilines corresponding to points in left image (first image) and
# drawing its lines on right image
lines2 = cv.computeCorrespondEpilines(pts1.reshape(-1,1,2), 1,F)
lines2 = lines2.reshape(-1,3)
img3,img4 = drawlines(img2,img1,lines2,pts2,pts1)

plt.subplot(121),plt.imshow(img5)
plt.subplot(122),plt.imshow(img3)
plt.show()

以下是我们的处理结果：

从左侧图像可以看出，所有极线都在图像右侧外的一个点汇聚。这个交汇点就是极点。

为了获得更好的效果，建议使用高分辨率且包含大量非共面点的图像。

练习

1、一个重要议题是相机的前向运动。此时在两幅图像中极点会出现在相同位置，而极线会从固定点发散。参见此讨论。

2、基础矩阵估计对匹配质量、异常值等非常敏感。当所有选定匹配点都位于同一平面时，情况会变得更糟。查看此讨论。

生成于 2025年4月30日 星期三 23:08:42，使用 doxygen 1.12.0 为 OpenCV 生成

从立体图像生成深度图

https://docs.opencv.org/4.x/dd/d53/tutorial_py_depthmap.html

目标

在本节课程中，

  • 我们将学习如何从立体图像创建深度图。

基础概念

在上节课中，我们学习了极线约束等基础概念及相关术语。我们还了解到，如果拥有同一场景的两幅图像，就能以直观的方式从中获取深度信息。下图及简单数学公式将验证这一原理（图片来源）：

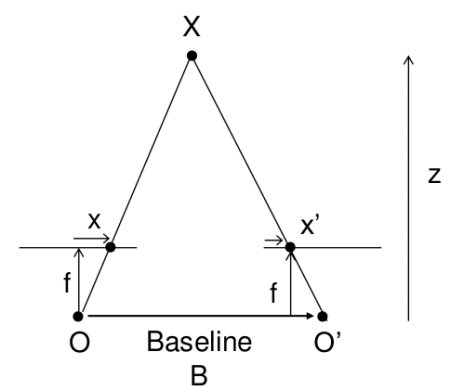
上图展示了一组相似三角形。通过建立等价方程可得到以下结果：

\[视差 = x - x' = \frac{Bf}{Z}\]

其中，\(x\)和\(x'\)分别表示三维场景点在图像平面上的对应点与各自相机中心之间的距离。\(B\)代表双相机间距（已知参数），\(f\)为相机焦距（已知参数）。简而言之，该公式表明场景点的深度与对应图像点及其相机中心距离差成反比。基于此原理，我们可以计算图像中所有像素的深度值。

该过程需要在两幅图像间寻找对应匹配点。此前我们已经了解极线约束如何加速并提升该操作的准确性。找到匹配点后即可计算视差。接下来我们将学习如何通过OpenCV实现这一过程。

代码

以下代码片段展示了一个创建视差图的简单流程。

python 复制代码 
import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt

imgL = cv.imread('tsukuba_l.png', cv.IMREAD_GRAYSCALE)
imgR = cv.imread('tsukuba_r.png', cv.IMREAD_GRAYSCALE)

stereo = cv.StereoBM.create(numDisparities=16, blockSize=15)
disparity = stereo.compute(imgL,imgR)
plt.imshow(disparity,'gray')
plt.show()

下图展示了原始图像（左）及其视差图（右）。可以看到结果中存在大量噪声污染。通过调整 numDisparities 和 blockSize 的数值，可以获得更好的效果。

熟悉 StereoBM 后，您需要微调以下参数以获得更平滑的结果：

  • texture_threshold：过滤掉纹理不足、无法进行可靠匹配的区域
  • Speckle range 和 size ：基于块的匹配器常在物体边界处产生"斑点"，此时匹配窗口会同时捕捉前景和背景。该场景中，匹配器还会在桌面的投影纹理上找到小的伪匹配。通过 speckle_size（视为斑点的最大像素数）和 speckle_range（判定为同一斑点的视差值相近度）参数控制的斑点滤波器可消除这些伪影
  • Number of disparities：滑动窗口的像素范围。值越大可见深度范围越广，但计算量也越大
  • min_disparity：从左侧像素的x坐标开始搜索的偏移量
  • uniqueness_ratio：后过滤步骤。若最佳匹配视差与搜索范围内其他视差相比优势不足，则过滤该像素。当纹理阈值和斑点过滤仍存在伪匹配时可调整此参数
  • prefilter_size 和 prefilter_cap：预处理阶段用于归一化图像亮度并增强纹理（为块匹配做准备），通常无需调整

这些参数需在算法初始化后通过专用设置器配置，例如 setTextureThreshold、setSpeckleRange、setUniquenessRatio 等。详见 cv::StereoBM 文档。

附加资源

练习

1、OpenCV示例中包含一个生成视差图及其3D重建的案例。请查看OpenCV-Python示例中的stereo_match.py文件。

生成于2025年4月30日 星期三 23:08:42，由doxygen 1.12.0为OpenCV生成

2-=025-07-19（六）

相关推荐
亲持红叶19 分钟前
神经网络常见激活函数 13-Softplus函数
人工智能·深度学习·神经网络
nightunderblackcat23 分钟前
[AI风堇]基于ChatGPT3.5+科大讯飞录音转文字API+GPT-SOVITS的模拟情感实时语音对话项目
人工智能·gpt·gpt-3
双翌视觉1 小时前
机器视觉的布料丝印应用
人工智能·数码相机·机器视觉
weixin_660096781 小时前
数据集下载网站
人工智能
WoShop商城源码1 小时前
短视频矩阵系统：选择与开发的全面指南
大数据·人工智能·其他·矩阵
飞哥数智坊1 小时前
Cursor 真正的对手！字节 TRAE SOLO 明日发布
人工智能·trae
Monkey的自我迭代2 小时前
量子计算与AI融合的技术突破与实践路径
人工智能·量子计算
花火|2 小时前
关于pytorch虚拟环境及具体bug问题修改
人工智能·pytorch·python
斟的是酒中桃2 小时前
【学习记录】智能客服小桃（进度更新ing）
人工智能·python·学习·语言模型·langchain·agent
Mr.小海3 小时前
AI编程工具对比：Cursor、GitHub Copilot与Claude Code
人工智能·低代码·chatgpt·github·aigc·copilot·ai编程
热门推荐
01全球最强模型Grok4，国内已可免费使用！（附教程）02Cursor Claude 模型无法使用的解决方法03KGG转MP3工具|非KGM文件|解密音频04【2025.7.18】更新vscode后所有.vue文件template标签后报红的临时解决办法，Vue - Official 插件3.0.2导致05集群聊天服务器---MySQL数据库的建立06【无标题】07Claude Code 最新版已经支持 Windows 安装使用！08身弱武修法：玄之又玄，奇妙之门09使用Ruby接入实时行情API教程102024电赛H题参考方案（+视频演示）——自动行使小车