1. 算法思想
多源 BFS(多源广度优先搜索)是广度优先搜索(BFS)的一种扩展形式,核心思想是从多个起点同时开始遍历,通过逐层扩散的方式求解 "多源最短路径" 或 "范围覆盖" 类问题。其本质是利用 BFS 的 "层级遍历" 特性,确保每个节点首次被访问时的路径长度为 "到最近源点的最短距离"。
多源 BFS 的核心思想
-
多起点初始化
与传统 BFS 从单个起点出发不同,多源 BFS 会将所有 "源点"(如矩阵中的所有 0、所有水域、所有边界节点等)同时加入队列,并标记其初始距离(通常为 0,因源点到自身的距离为 0)。这些源点是问题中具有特殊意义的节点,例如 "最短路径的起点""扩散的起始点"。
-
层级扩散与距离计算
从队列中依次取出节点,对其相邻节点(如上下左右四个方向)进行遍历。若相邻节点未被访问过,则将其距离更新为 "当前节点距离 + 1"(因 BFS 层级遍历的特性,此距离为该节点到最近源点的最短距离),并将其加入队列。整个过程中,所有节点按照 "到最近源点的距离" 从小到大的顺序被访问,确保距离计算的最优性。
-
终止条件
当队列为空时,所有可达节点均已被访问,此时每个节点的距离即为 "到最近源点的最短距离"。
多源 BFS 的适用场景
多源 BFS 主要用于解决 **"从多个起点出发,求所有节点到最近起点的最短距离"** 类问题,典型场景包括:
- 01 矩阵:计算每个 1 到最近 0 的距离(如前文代码示例)。
- 飞地数量:标记所有与边界相连的节点,剩余节点为飞地(如前文代码示例)。
- 高度矩阵:以水域为起点,构建相邻高度差不超过 1 的矩阵(如前文代码示例)。
- 疫情扩散:计算所有区域到最近疫区的最短传播时间。
多源 BFS 的优势
- 效率高:相比 "从每个节点单独出发做 BFS" 的暴力解法,多源 BFS 只需遍历所有节点一次,时间复杂度为 O (N×M)(N、M 为矩阵的行数和列数),避免了重复计算。
- 结果最优:BFS 的层级遍历特性保证了每个节点首次被访问时的距离是最短路径,无需二次更新。
与传统 BFS 的对比
- 起点数量:传统 BFS 只有 1 个起点,多源 BFS 有多个(≥2 个)起点。
- 适用问题:传统 BFS 用于单源最短路径问题,多源 BFS 用于多源最短路径(求最近源点)问题。
- 初始化:传统 BFS 将单个起点入队并设距离为 0;多源 BFS 将所有源点入队并设距离为 0。
- 时间复杂度:两者在单轮遍历中均为 O (N×M),但多源 BFS 避免了多轮重复计算,整体效率更高。
2. 例题
2.1 矩阵

核心思路如下:
核心思路
-
多源起点初始化
- 将矩阵中所有值为
0的位置视为 BFS 的起点,这些点的距离直接标记为0。 - 将所有起点加入队列,形成多源 BFS 的初始状态。
- 将矩阵中所有值为
-
BFS 逐层扩展
- 从队列中取出每个起点(或已访问的点),向其四个方向(上、下、左、右)进行扩展。
- 若扩展后的新位置合法且未被访问过(距离为
-1),则更新其距离为当前点的距离加1,并将新位置加入队列。
-
距离矩阵的单调性
- BFS 的特性保证了每个点第一次被访问时的路径长度(距离)是最短的,因此无需二次更新。
- 所有点按照到最近零的距离从小到大的顺序被访问,确保结果的正确性。
关键点解释
-
为什么用多源 BFS?
从所有零同时开始 BFS,避免了从每个点单独出发的重复计算,时间复杂度优化为 O (N*M)。
-
方向数组的作用
dx[4]和dy[4]数组定义了四个方向的偏移量,用于快速遍历相邻位置。 -
距离矩阵的初始化
dist矩阵初始化为-1,既表示未访问状态,又方便在扩展时判断是否需要更新距离。
算法伪代码
1. 初始化距离矩阵 dist,所有值为 -1
2. 将所有值为 0 的位置加入队列,并设置其距离为 0
3. 当队列不为空时:
- 取出队首元素 (a, b)
- 遍历四个方向:
- 计算新位置 (x, y)
- 若 (x, y) 合法且未被访问:
- 更新 dist[x][y] = dist[a][b] + 1
- 将 (x, y) 加入队列
4. 返回 dist 矩阵复杂度分析
- 时间复杂度:O (N*M),每个点最多被访问一次。
- 空间复杂度:O (N*M),主要用于存储距离矩阵和队列。
cpp
vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
typedef pair<int, int> PII;
int n = mat.size(), m = mat[0].size();
int dx[4] = {0, 0, 1, -1};
int dy[4] = {1, -1, 0, 0};
vector<vector<int>> dist(n, vector<int>(m, -1));
queue<PII> q;
// 找到所有的零
for(int i = 0; i < n; ++i)
{
for(int j = 0; j < m; ++j)
if(mat[i][j] == 0)
{
q.push({i, j});
dist[i][j] = 0;
}
}
while(q.size())
{
auto [a, b] = q.front();
q.pop();
for(int k = 0; k < 4; ++k)
{
int x = a + dx[k], y = b + dy[k];
if(x >= 0 && x < n && y >= 0 && y < m && dist[x][y] == -1)
{
dist[x][y] = dist[a][b] + 1;
q.push({x, y});
}
}
}
return dist;
}2.2 飞地的数量
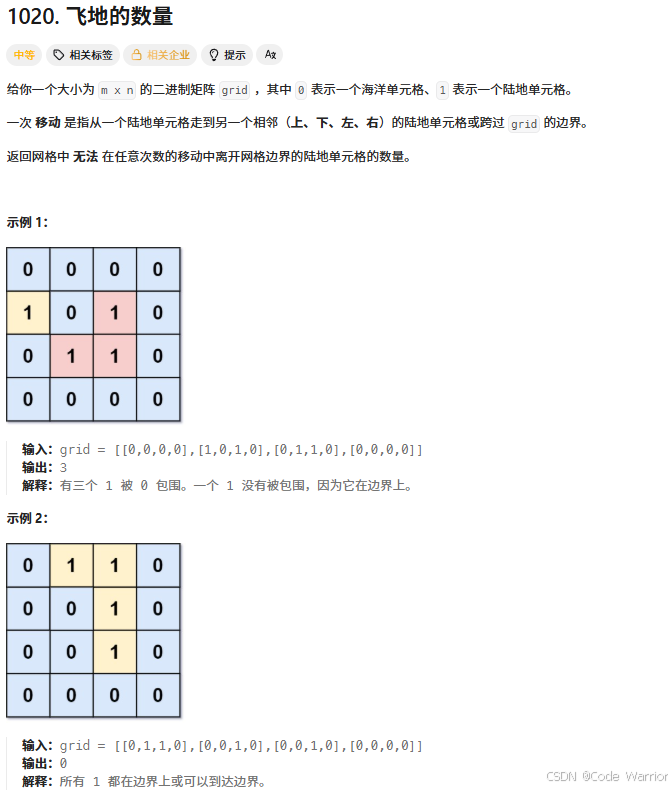
核心思路如下:
核心思路
-
边界扫描与标记
- 遍历矩阵的四条边界,将所有边界上的陆地(值为
1)标记为已访问,并加入 BFS 队列。这些陆地可以通向矩阵外部。
- 遍历矩阵的四条边界,将所有边界上的陆地(值为
-
BFS 扩散访问
- 从边界陆地出发,使用 BFS 向内部扩散,标记所有与边界相连的陆地。这些陆地同样可以通向外部。
-
统计内部陆地
- 遍历整个矩阵,统计所有未被标记的陆地(值为
1且未被访问),这些陆地即为无法到达边界的 "飞地"。
- 遍历整个矩阵,统计所有未被标记的陆地(值为
关键点解释
-
为什么从边界出发?
从边界陆地开始 BFS 可以高效标记所有可到达边界的区域,剩余未被标记的陆地必然无法到达边界。
-
访问标记数组
dist用于记录每个位置是否被访问过,避免重复处理。初始化为
false,被访问后设为true。 -
方向数组的作用
dx[4]和dy[4]数组定义四个方向的偏移量,用于快速遍历相邻位置。
算法伪代码
1. 初始化访问标记矩阵 dist,所有值为 false
2. 将四条边界上的所有陆地加入队列,并标记为已访问
3. 当队列不为空时:
- 取出队首元素 (a, b)
- 遍历四个方向:
- 计算新位置 (x, y)
- 若 (x, y) 合法、是陆地且未被访问:
- 标记 dist[x][y] 为 true
- 将 (x, y) 加入队列
4. 遍历整个矩阵,统计所有满足 grid[i][j] == 1 且 !dist[i][j] 的点数量复杂度分析
- 时间复杂度:O (N*M),每个点最多被访问一次。
- 空间复杂度:O (N*M),主要用于存储访问标记矩阵和 BFS 队列。
cpp
class Solution {
public:
int numEnclaves(vector<vector<int>>& grid) {
typedef pair<int, int> PII;
int dx[4] = {0, 0, 1, -1};
int dy[4] = {1, -1, 0, 0};
int n = grid.size(), m = grid[0].size();
vector<vector<bool>> dist(n, vector<bool>(m, false));
queue<PII> q;
// 把出口的1记录下来
for(int i = 0; i < n; ++i)
{
if(grid[i][0] == 1)
{
q.push({i, 0});
dist[i][0] = true;
}
if(grid[i][m - 1] == 1)
{
q.push({i, m - 1});
dist[i][m - 1] = true;
}
}
for(int i = 1; i < m - 1; ++i)
{
if(grid[0][i] == 1)
{
q.push({0, i});
dist[0][i] = true;
}
if(grid[n - 1][i] == 1)
{
q.push({n - 1, i});
dist[n - 1][i] = true;
}
}
while(q.size())
{
auto [a, b] = q.front();
q.pop();
for(int k = 0; k < 4; ++k)
{
int x = a + dx[k], y = b + dy[k];
if(x >= 0 && x < n && y >= 0 && y < m && grid[x][y] == 1 && !dist[x][y])
{
dist[x][y] = true;
q.push({x, y});
}
}
}
int ret = 0;
for(int i = 0; i < n; ++i)
{
for(int j = 0; j < m; ++j)
{
if(grid[i][j] == 1 && !dist[i][j])
++ret;
}
}
return ret;
}
};2.3 地图中的最高点
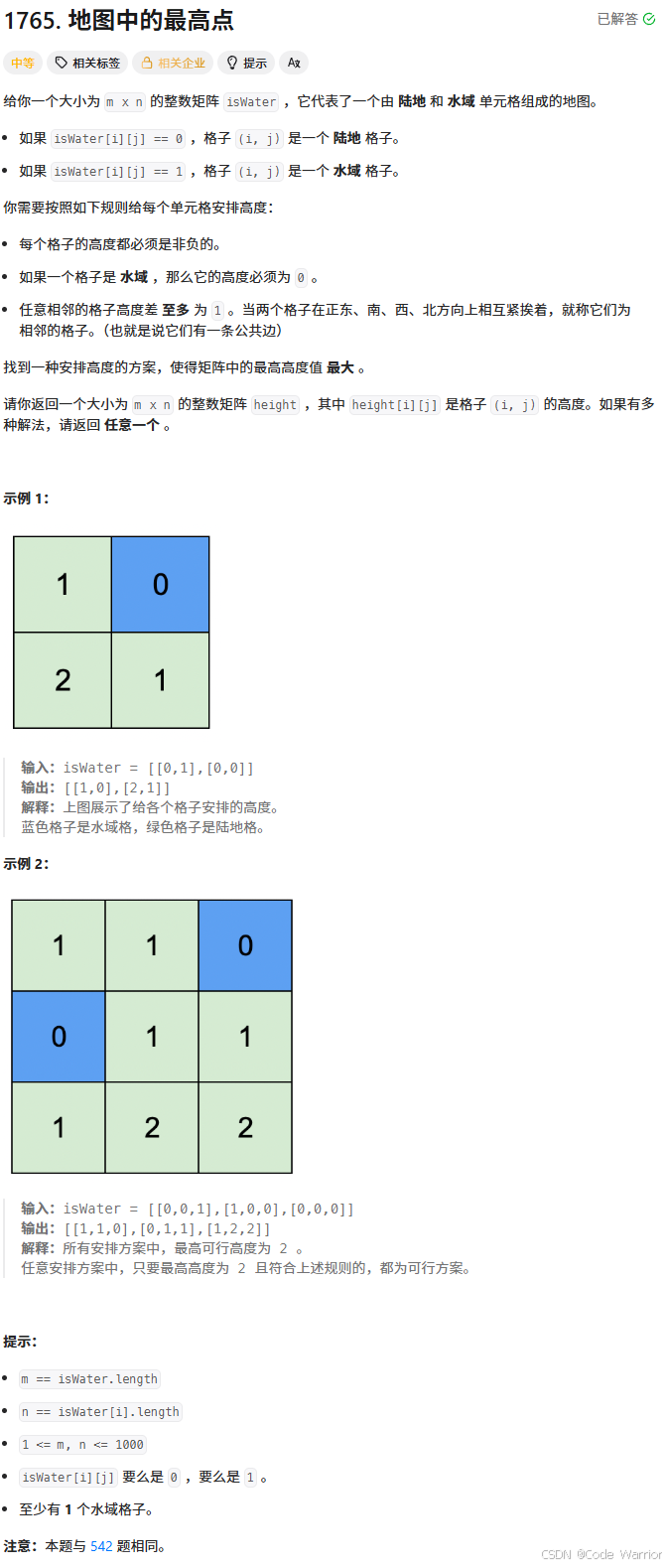
核心思路如下:
核心思路
-
多源起点初始化
- 将所有水域格子(值为
1)视为 BFS 的起点,高度直接设为0。 - 将所有起点加入队列,形成多源 BFS 的初始状态。
- 将所有水域格子(值为
-
BFS 逐层扩展
- 从队列中取出每个已访问的格子,向其四个方向(上、下、左、右)进行扩展。
- 若扩展后的新位置合法且未被访问过(高度为
-1),则将其高度设为当前格子的高度加1,并加入队列。
-
高度矩阵的单调性
- BFS 的特性保证了每个格子第一次被访问时的高度是最小可能值,确保相邻格子高度差不超过 1。
- 所有格子按照到最近水域的最短路径长度递增的顺序被访问,生成的高度矩阵满足题目要求。
关键点解释
-
为什么用多源 BFS?
从所有水域同时开始 BFS,能确保每个格子的高度是到最近水域的最短距离,避免了从每个点单独出发的重复计算。
-
方向数组的作用
dx[4]和dy[4]数组定义四个方向的偏移量,用于快速遍历相邻位置。 -
高度矩阵的初始化
dist矩阵初始化为-1,既表示未访问状态,又方便在扩展时判断是否需要更新高度。
算法伪代码
1. 初始化高度矩阵 dist,所有值为 -1
2. 将所有水域格子(值为 1)加入队列,并设置其高度为 0
3. 当队列不为空时:
- 取出队首元素 (a, b)
- 遍历四个方向:
- 计算新位置 (x, y)
- 若 (x, y) 合法且未被访问:
- 更新 dist[x][y] = dist[a][b] + 1
- 将 (x, y) 加入队列
4. 返回高度矩阵 dist复杂度分析
- 时间复杂度:O (N*M),每个格子最多被访问一次。
- 空间复杂度:O (N*M),主要用于存储高度矩阵和 BFS 队列。
cpp
class Solution {
public:
vector<vector<int>> highestPeak(vector<vector<int>>& isWater) {
typedef pair<int, int> PII;
int dx[4] = {1, -1, 0, 0};
int dy[4] = {0, 0, 1, -1};
int n = isWater.size(), m = isWater[0].size();
vector<vector<int>> dist(n, vector<int>(m, -1));
queue<PII> q;
for(int i = 0; i < n; ++i)
{
for(int j = 0; j < m; ++j)
if(isWater[i][j] == 1) // 找到所有的水域格子
{
q.push({i, j});
dist[i][j] = 0;
}
}
while(q.size())
{
auto [a, b] = q.front();
q.pop();
for(int k = 0; k < 4; ++k)
{
int x = a + dx[k], y = b + dy[k];
if(x >= 0 && x < n && y >= 0 && y < m && dist[x][y] == -1)
{
dist[x][y] = dist[a][b] + 1;
q.push({x, y});
}
}
}
return dist;
}
};2.4 地图分析

核心算法步骤如下:
核心算法步骤
-
初始化与边界判断
- 创建与原矩阵同尺寸的距离矩阵
dist,初始值为-1(标记未访问)。 - 遍历矩阵,将所有陆地(值为
1)加入 BFS 队列,并将其距离设为0(陆地到自身的距离为 0)。 - 特殊情况处理:若全为陆地或全为海洋,直接返回
-1。
- 创建与原矩阵同尺寸的距离矩阵
-
多源 BFS 扩散计算距离
- 从所有陆地同时出发,通过 BFS 向四周海洋(值为
0)扩散:- 每次取出队列中的陆地位置
(a,b),遍历其上下左右四个方向。 - 若相邻位置
(x,y)是未访问的海洋(dist[x][y] == -1),则更新其距离为dist[a][b] + 1,并加入队列。
- 每次取出队列中的陆地位置
- 实时记录最大距离
ret(即海洋到最近陆地的最远距离)。
- 从所有陆地同时出发,通过 BFS 向四周海洋(值为
-
返回结果
- BFS 结束后,
ret即为所求的最远距离。
- BFS 结束后,
关键逻辑解析
-
多源 BFS 的作用 :
从所有陆地同时开始扩散,保证每个海洋第一次被访问时的距离是 "到最近陆地的最短距离",避免了从单个陆地出发的重复计算,效率更高。
-
方向数组的作用 :
dx和dy数组定义四个方向的偏移量(上下左右),用于快速遍历相邻位置。 -
距离矩阵的意义 :
dist矩阵既标记访问状态(-1为未访问),又存储每个海洋到最近陆地的距离,一举两得。
算法伪代码
1. 初始化距离矩阵dist为-1,创建队列q
2. 遍历矩阵,将所有陆地(值为1)加入q,设置dist[i][j] = 0
3. 若q为空或q大小等于矩阵总元素数,返回-1
4. 初始化最大距离ret = 0
5. 当q不为空时:
- 取出队首元素(a, b)
- 遍历四个方向,计算新位置(x, y)
- 若(x, y)合法且未访问(dist[x][y] == -1):
- dist[x][y] = dist[a][b] + 1
- ret = max(ret, dist[x][y])
- 将(x, y)加入q
6. 返回ret复杂度分析
- 时间复杂度:O (n*m),每个元素最多被访问一次。
- 空间复杂度:O (n*m),用于存储距离矩阵和 BFS 队列。
cpp
class Solution {
public:
int maxDistance(vector<vector<int>>& grid) {
typedef pair<int, int> PII;
int dx[4] = {0, 0, 1, -1};
int dy[4] = {1, -1, 0, 0};
int n = grid.size(), m = grid[0].size();
vector<vector<int>> dist(n, vector<int>(m, -1));
int ret = 0;
queue<PII> q;
for(int i = 0; i < n ; ++i)
{
for(int j = 0; j < m; ++j)
if(grid[i][j] == 1) // 找到所有的陆地
{
q.push({i, j});
dist[i][j] = 0;
}
}
if(!q.size() || q.size() == n * m) return -1;
while(q.size())
{
auto [a, b] = q.front();
q.pop();
for(int k = 0; k < 4; ++k)
{
int x = a + dx[k], y = b + dy[k];
if(x >= 0 && x < n && y >= 0 && y < m && dist[x][y] == -1)
{
dist[x][y] = dist[a][b] + 1;
q.push({x, y});
ret = max(ret, dist[x][y]);
}
}
}
return ret;
}
};