
🔥个人主页:艾莉丝努力练剑
❄专栏传送门:《C语言》、《数据结构与算法》、C语言刷题12天IO强训、LeetCode代码强化刷题
🍉学习方向:C/C++方向
⭐️人生格言:为天地立心,为生民立命,为往圣继绝学,为万世开太平

**重要提醒:**为什么我们要学那么多的数据结构?这是因为没有一种数据结构能够去应对所有场景。我们在不同的场景需要选择不同的数据结构,所以数据结构没有谁好谁坏之分,而评估数据结构的好坏要针对场景,如果在一种场景下我们需要频繁地对头部进行插入删除操作,那么这个时候我们用链表;但是如果对尾部进行插入删除操作比较频繁,那我们用顺序表比较好。
因此,不同的场景我们选择不同的数据结构。
**前言:**本篇文章,我们继续来看二叉树相关的知识点,在初阶的数据结构与算法阶段,我们把知识点分成三部分,复杂度作为第一部分,顺序表和链表、栈和队列、二叉树为第二部分,排序为第二部分,我们之前已经介绍完了第一部分:算法复杂度,本文我们将正式开始学习第二部分中的二叉树部分内容啦。
注意,二叉树的学习需要一定的基础,涉及到【函数栈帧的创建与销毁】,而且二叉树尤其是链式结构二叉树基本上是递归算法的暴力美学。
【深入详解】函数栈帧的创建与销毁:寄存器、压栈、出栈、调用、回收空间
详解TOP-K问题 会涉及到前面C语言部分**【文件操作** 】的内容,忘记了的友友链接放在下面了**------**
【掌握文件操作】(上):二进制文件和文本文件、文件的打开和关闭、文件的顺序读写
【掌握文件操作】(下):文件的顺序读写、文件的随机读写、文件读取结束的判定、文件缓冲区
目录
正文
三、二叉树的顺序结构:堆
(四)向上、向下调整算法
1、建堆
排升序------建大堆;
排降序------建小堆。
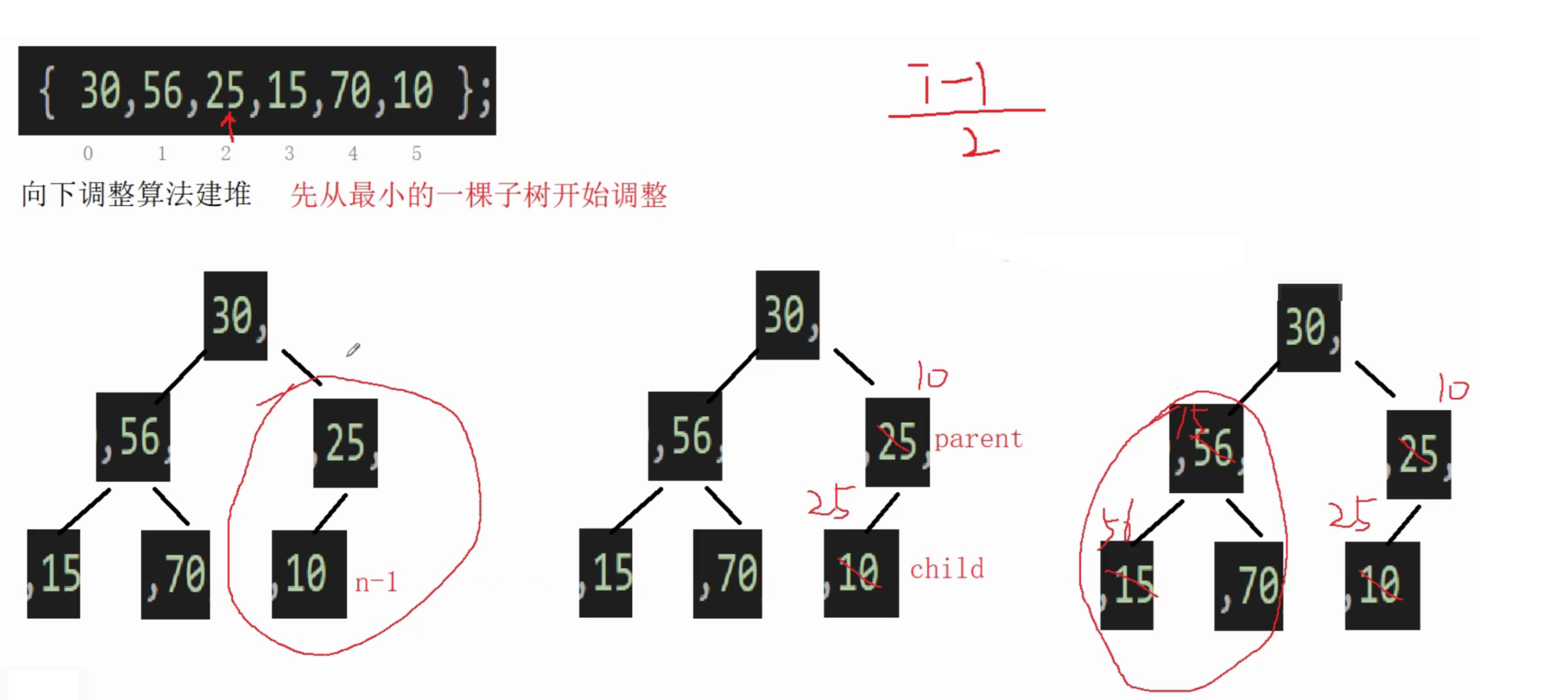
(1)向下调整算法------建堆
向下调整算法有一个前提:左右子树必须是一个堆,才能调整。
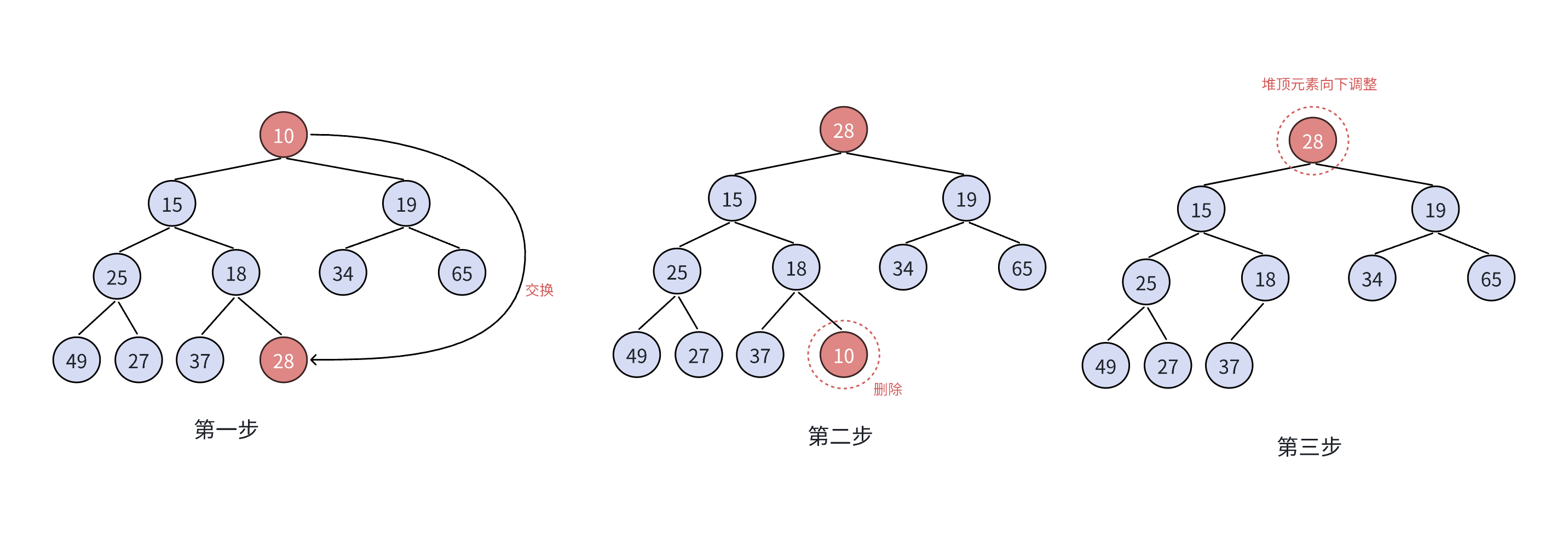
删除堆是删除堆顶的数据,将堆顶的数据根最后一个数据一换,然后删除数组最后一个数据,再进行向下调整算法。


cpp
//向下调整算法------建堆
//乱序数组------------建堆
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(arr, i, n);
}(2)向上调整算法------建堆
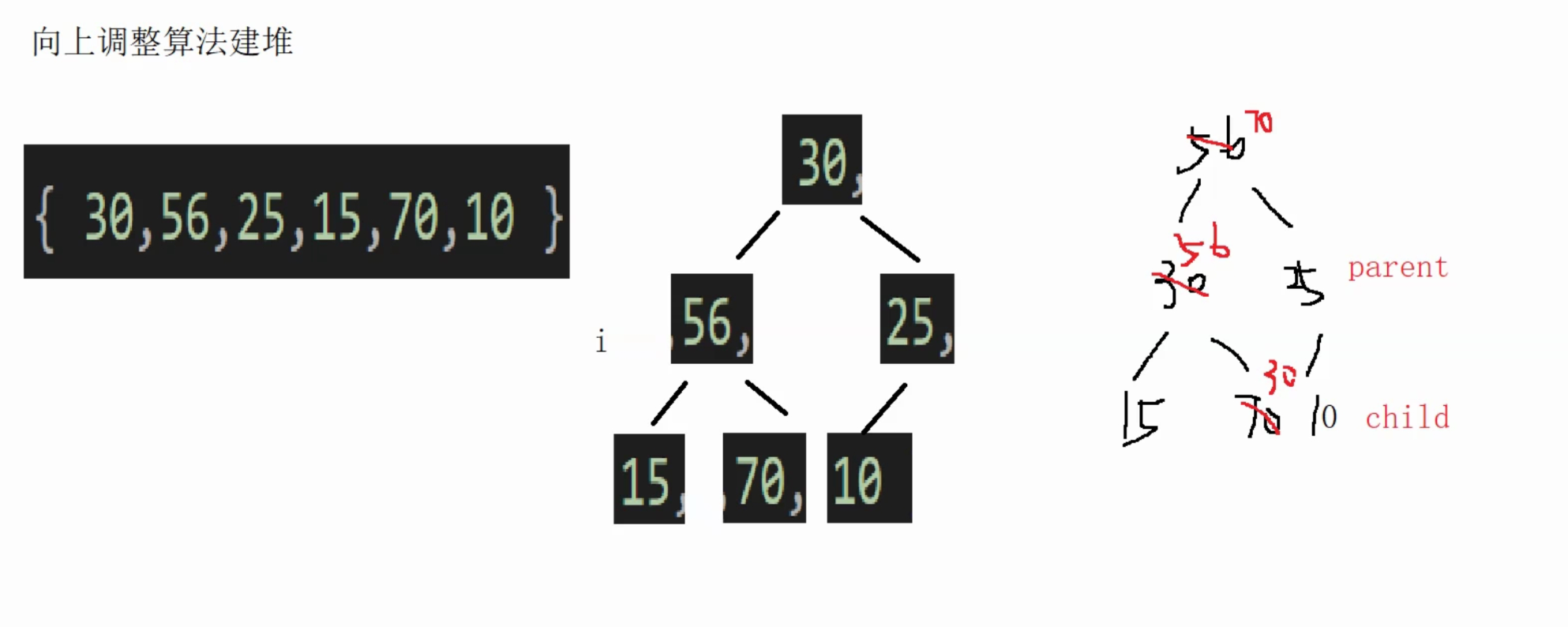

cpp
for (int i = 0; i < n; i++)
{
AdjustUp(arr, i);
}可以大堆、小堆都试一下------
大堆:

小堆:

2、向上、向下调整算法的时间复杂度以及证明
(1)向上调整算法
时间复杂度:O(nlogn)****。
证明:

我们错位相减一下:
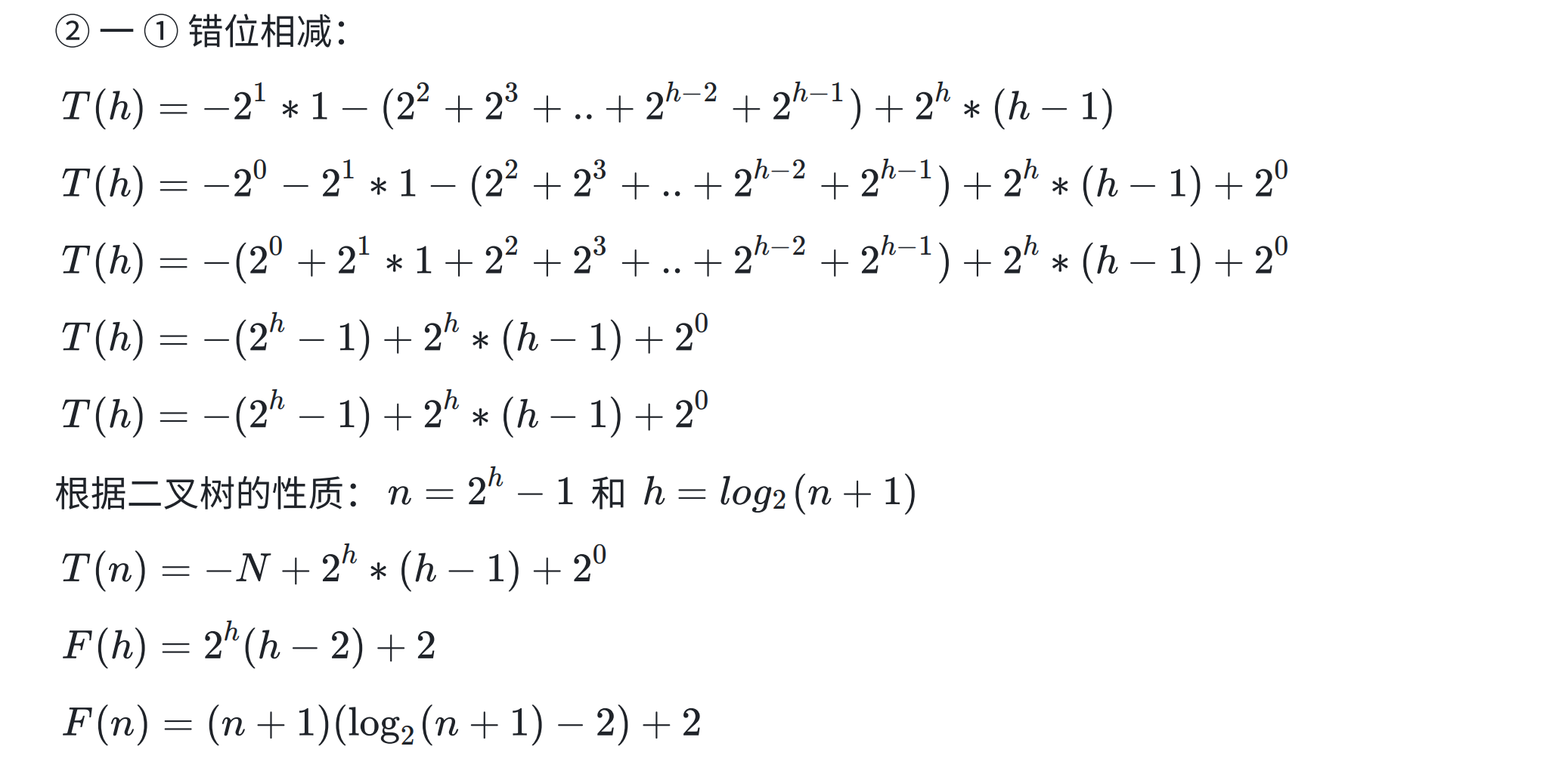
向上调整算法建堆的时间复杂度为:O(n*logn)。
(2)向下调整算法
时间复杂度:O(n)****。
证明:
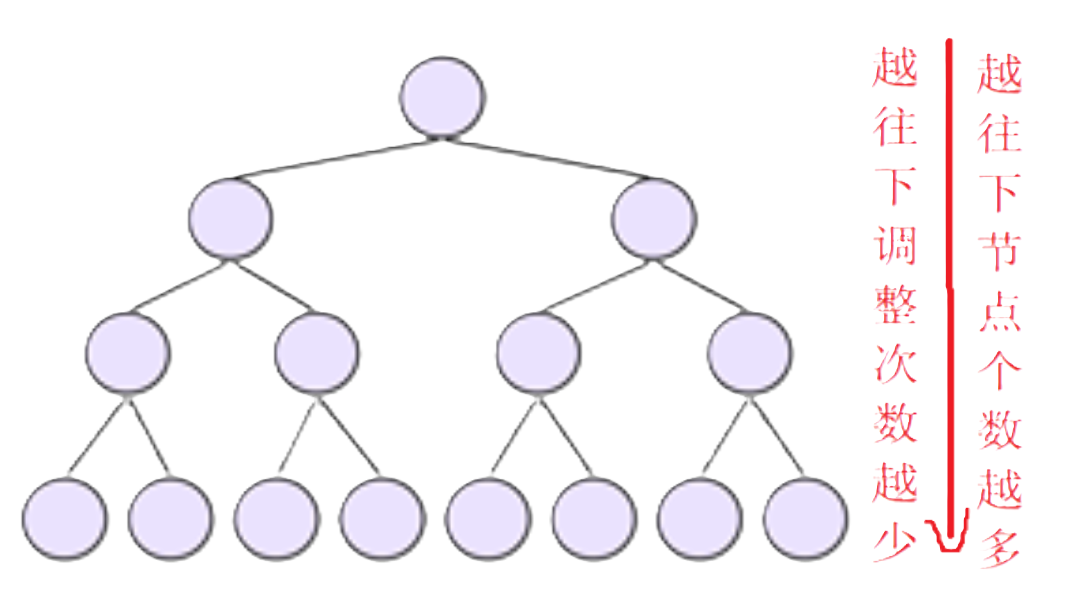

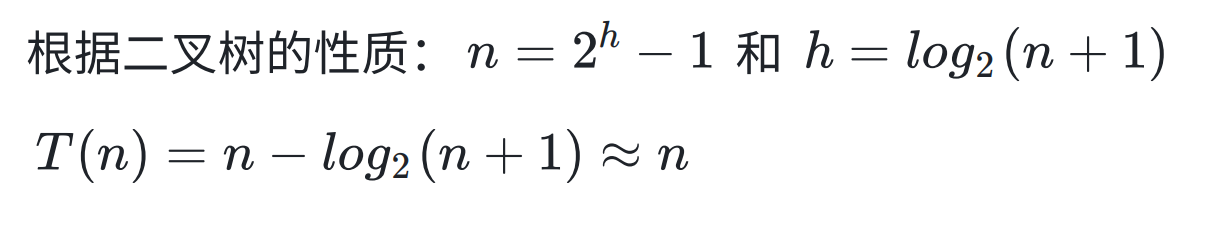
向下调整算法建堆的时间复杂度为:O(n)。
3、堆排序时间复杂度计算证明
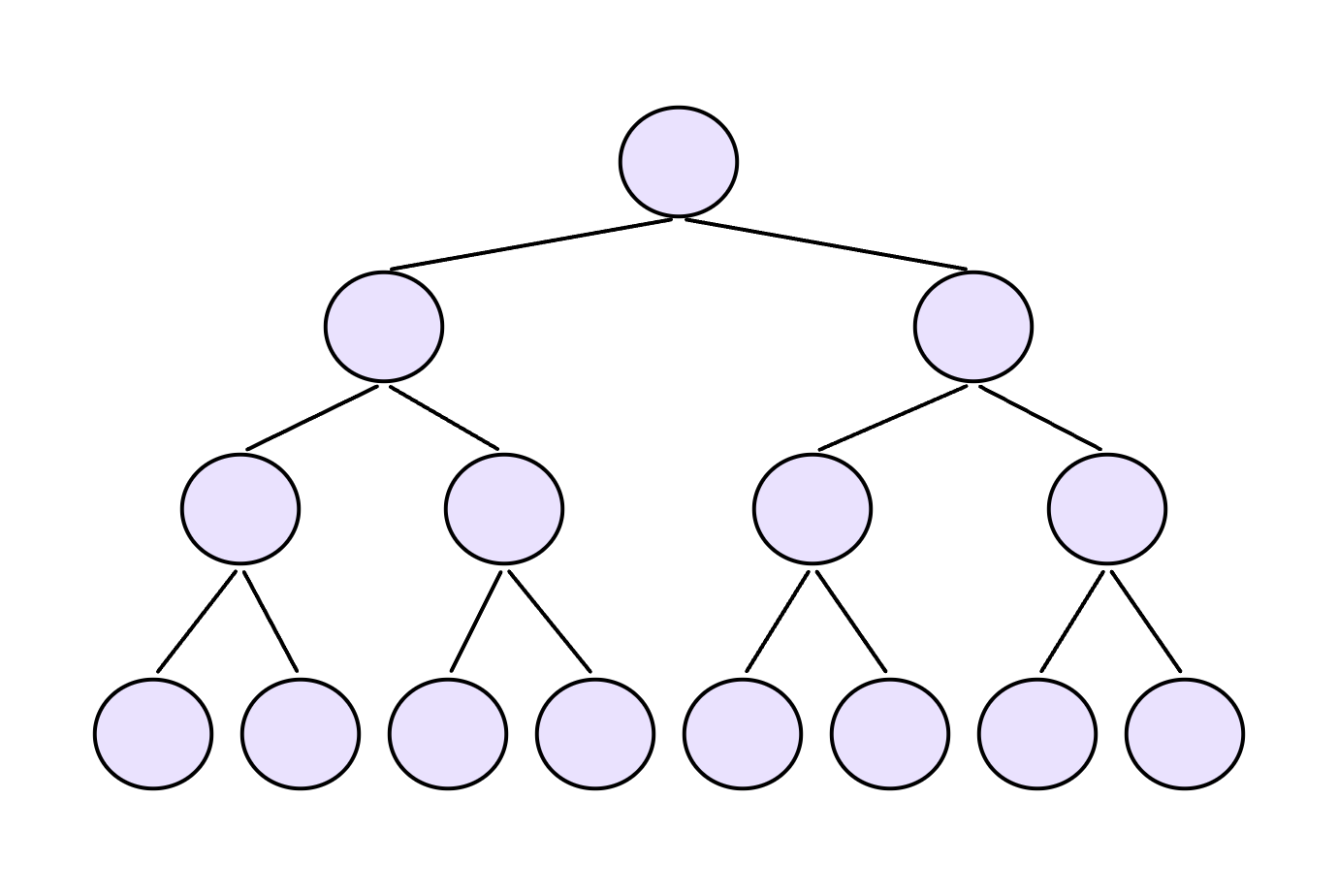
证明:
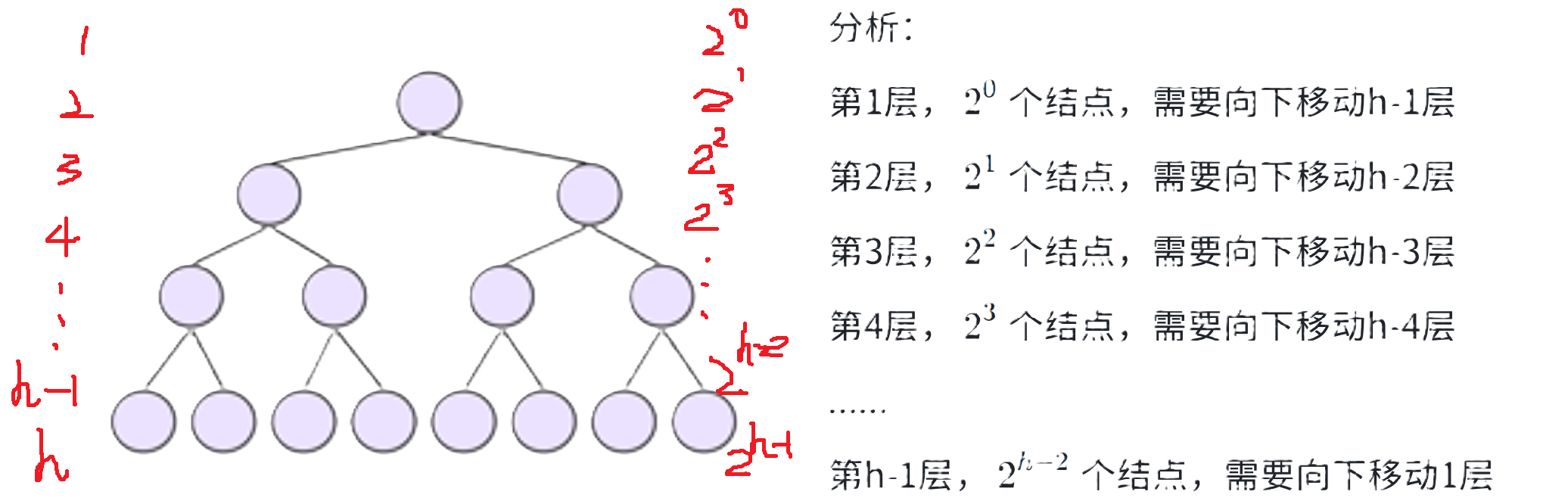
分析:
第1层,2^0个结点,交换到根结点后,需要向下移动0层
第2层,2^1个结点,交换到根结点后,需要向下移动1层
第3层,2^2个结点,交换到根结点后,需要向下移动2层
第4层,2^3个结点,交换到根结点后,需要向下移动3层
......
第h层,2^(h-1)个结点,交换到根结点后,需要向下移动h-1层
通过分析发现,堆排序第二个循环中的向下调整与建堆中的向上调整算法时间复杂度计算一致。
因此,堆排序的时间复杂度为O(n + n ∗ log n),即O(nlog n)。
(五)TOP-K问题详解


如果面试官这样问你:假设有10亿个整数,需要申请多大的内存?
已知:
1G = 1024MB = 1024 * 1024KB = 1024 * 1024 * 1024byte
那么 10亿 * 4 = 4G
假设只有1G内存,该怎么办?我们可以划分等分------
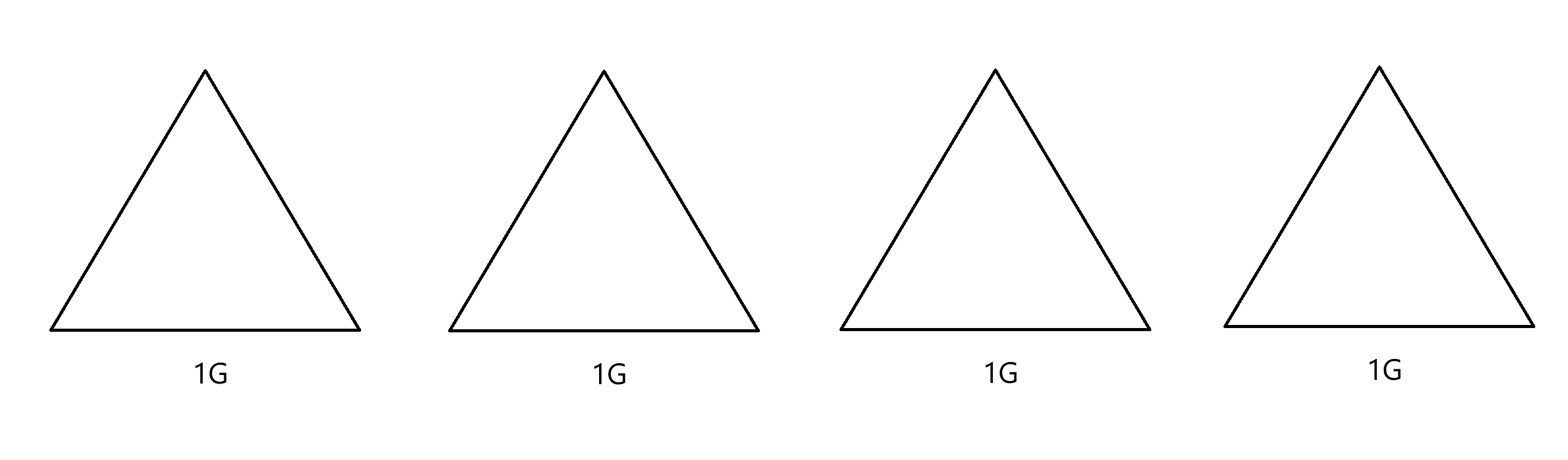
我把10亿个数据分成四等分,每等分1个G,我们先消耗1个G取第一份的数据,建堆取最大的几个数据,剩下的每一份都是这样,也就是说这个内存我们循环使用,每次都使用1个G大小的内存。 这样可以吗?可以。
但是面试官可不会这么轻易地放过你,接着问:
假设现在只有1KB的内存怎么办?

找最大的前K个数据,建小堆,遍历剩下的数据和堆顶比,比堆顶要大的就和堆顶交换;
找最小的前K个数据,建大堆,遍历剩下的数据和堆顶比,比堆顶要小就和堆顶交换。
cpp
void CreateNDate()
{
// 造数据
int n = 100000;
srand(time(0));
const char* file = "data.txt";
FILE* fin = fopen(file, "w");
if (fin == NULL)
{
perror("fopen error");
return;
}
for (int i = 0; i < n; ++i)
{
int x = (rand() + i) % 1000000;
fprintf(fin, "%d\n", x);
}
fclose(fin);
}代码演示:
cpp
void TopK()
{
int k = 0;
printf("请输入K:");
scanf("%d", &k);
const char* file = "data.txt";
FILE* fout = fopen(file, "r");//fout表示读取文件
if (fout == NULL)
{
perror("fopen fail!");
exit(1);
}
//申请空间大小为k的整型数组
int* minHeap = (int*)malloc(sizeof(int) * k);
if (minHeap == NULL)
{
perror("malloc fail!");
exit(2);
}
//读取文件中k个数据放到数组中
for (int i = 0; i < k; i++)
{
fscanf(fout, "%d", &minHeap[i]);
}
//数组调整建堆------向下调整建堆
//找最大的前K个数,建小堆
for (int i = (k - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(minHeap, i, k);
}
//遍历剩下的n-k个数,跟堆顶比较,谁大谁入堆(堆顶)
int data = 0;
while (fscanf(fout,"%d",&data) != EOF)
{
if (data > minHeap[0])
{
minHeap[0] = data;
AdjustDown(minHeap, 0, k);
}
}
//打印堆顶的值
for (int i = 0; i < k; i++)
{
printf("%d ", minHeap[i]);
}
printf("\n");
fclose(fout);
}
int main()
{
//CreateNDate();
TopK();
return 0;
}
我们测试一下------
不知道这几个值对不对,我们手动输入几个值试试:
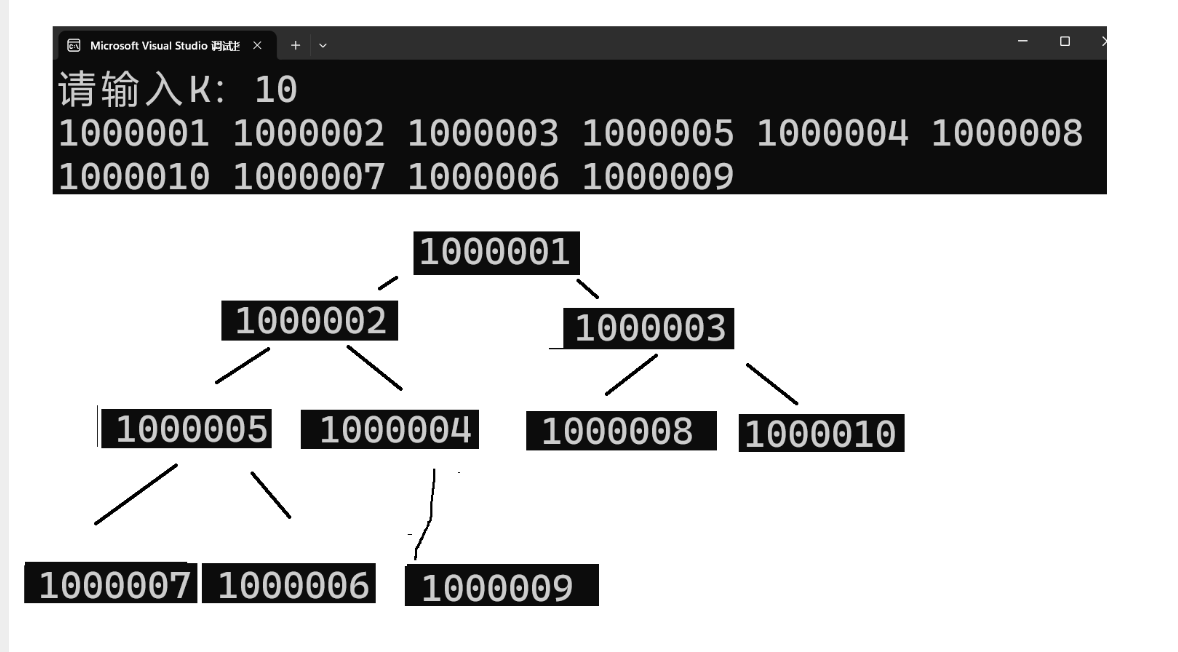
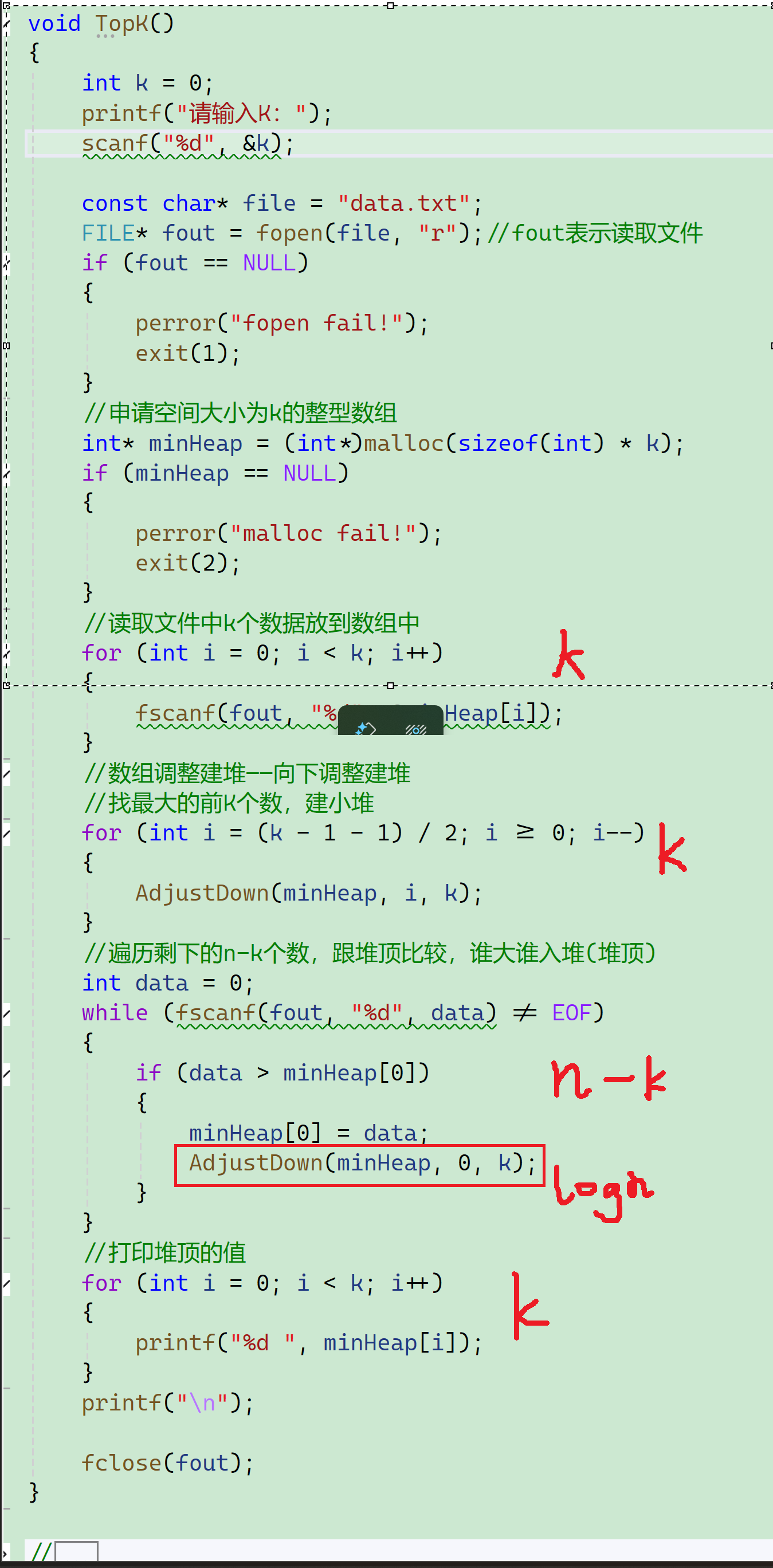

所以这就是对于时间复杂度的推理:
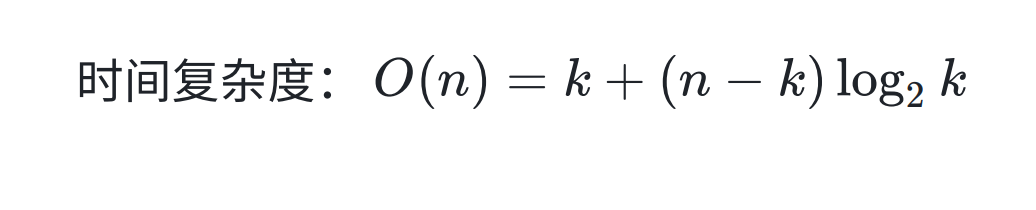
到这里堆的所有内容都介绍完了。
结尾
函数栈帧的创建与销毁、文件操作相关博客的链接,博主已经放在正文前面了,有需要的友友自取。由于本专栏的文章数量越来越多,每次挂链接都是一件非常枯燥且费时的事情,因此,从本篇开始,【数据结构】专栏的【传送门】环节除了相关文章之外只挂两篇内容无关文章的链接------前一篇文章以及【【数据结构与算法】数据结构初阶:详解顺序表和链表(三)------单链表(上)】
【数据结构与算法】数据结构初阶:详解二叉树(二)------堆
【数据结构与算法】数据结构初阶:详解栈和队列(下)------队列
本期内容需要回顾的C语言知识如下面的截图中所示(指针博主写了6篇,列出来有水字数嫌疑了,就只放指针第六篇的网址,博主在指针(六)把指针部分的前五篇的网址都放在【往期回顾】了,点击【传送门】就可以看了)。
大家如果对前面部分的知识点印象不深,可以去上一篇文章的结尾部分看看,博主把需要回顾的知识点相关的博客的链接都放在上一篇文章了,上一篇文章的链接博主放在下面了:
【数据结构与算法】数据结构初阶:详解顺序表和链表(三)------单链表(上)
**结语:**本篇文章到这里就结束了,对数据结构的二叉树知识感兴趣的友友们可以在评论区留言,博主创作时可能存在笔误,或者知识点不严谨的地方,大家多担待,如果大家在阅读的时候发现了行文有什么错误欢迎在评论区斧正,再次感谢友友们的关注和支持!