目录
[37.力扣. 1576替换所有的问号](#37.力扣. 1576替换所有的问号)
[37.1 题目解析：](#37.1 题目解析：)
[37.2 算法思路：](#37.2 算法思路：)
[37.3 代码演示：](#37.3 代码演示：)
[37.4 总结反思：](#37.4 总结反思：)
[38. 力扣495 提莫攻击](#38. 力扣495 提莫攻击)
[38.1 题目解析：](#38.1 题目解析：)
[38.2 算法思路：](#38.2 算法思路：)
[38.3 代码演示：](#38.3 代码演示：)
[38.4 总结反思：](#38.4 总结反思：)
[39. 力扣6 Z字形变化](#39. 力扣6 Z字形变化)
[39.1 题目解析：](#39.1 题目解析：)
[39.2 算法思路：](#39.2 算法思路：)
[39.3 代码演示：](#39.3 代码演示：)
[39.4 总结反思：](#39.4 总结反思：)
[40. 力扣 38 外观数列](#40. 力扣 38 外观数列)
[41.1 题目解析：](#41.1 题目解析：)
[41.2 算法思路：](#41.2 算法思路：)
[41.3 代码演示：](#41.3 代码演示：)
[41.4 总结反思：](#41.4 总结反思：)
[42. 力扣 1419 数青蛙](#42. 力扣 1419 数青蛙)
[42.1 题目解析：](#42.1 题目解析：)
[42.2 算法思路：](#42.2 算法思路：)
[42.3 代码演示：](#42.3 代码演示：)
[42.4 总结反思：](#42.4 总结反思：)
37.力扣. 1576替换所有的问号
37.1 题目解析：
今天咱们要学一个新算法，就是模拟算法。这类题的特点就是：比着葫芦画瓢（题目中已经告诉你该怎么做了）。那么考察你的就是代码能力，能不能把思路转化为代码，这个很重要。
1.先模拟一遍算法流程（一定要在演草纸上过一遍流程）
2.把流程转化为代码
37.2 算法思路：
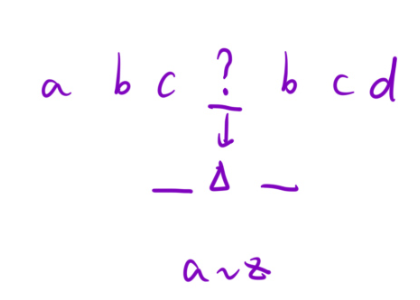
就是，咱们需要先找到问号在哪个位置，找到之后，在寻找'a'与'z'之间的字符，确保这个字符填到这里不与问号左右的字符重复即可。（返回一种结果就可以了）
但是需要注意一个细节：
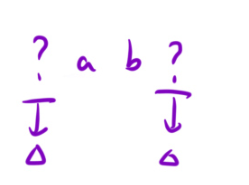
这个情况，就是如果说问号在第一个位置，只要确保问号与右边的不同即可。如果问号在最后一个位置，只要确保最后一个位置的问号代表的字符与左边的字符不同即可。
37.3 代码演示：
cpp
string modifyString(string s) {
int n = s.size();
for (int i = 0; i < n; i++)
{
if (s[i] == '?')//先找到问好在哪里
{
for (char ch = 'a'; ch <= 'z'; ch++)
{
if ((i == 0 || ch != s[i - 1]) && (i == n - 1 || ch != s[i + 1]))//如果说i等于0，那么只需要判断右面的不等于ch即可。
{
s[i] = ch;
break;
}
}
}
}
return s;
}
int main()
{
string s("?zs");
cout << modifyString(s) << endl;
return 0;
}37.4 总结反思：
基本的做题方法就是这样，注意：模拟的题一定要去找规律才可以。
38. 力扣495 提莫攻击
38.1 题目解析：
这道题很有意思，我个人认为就是游戏里面的掉血的计算，这个要是不会做，那我只能说，你以后要是做游戏开发，人物血量你都掉不明白哈哈哈哈，说着玩的，大家不要当真。
38.2 算法思路：
题目的意思已经很明显了，所以咱们只需要照着葫芦画瓢即可。这里基本也可以找到规律，就是如果说你的第二个元素减去第一个元素大于duration的话，说明，这个时候，是可以直接加上duration的。否则，就需要先加上第二个元素与第一个元素的差再加上duration。（这个其实是边界情况）
OK，咱们直接来看代码：
38.3 代码演示：
cpp
int findPoisonedDuration(vector<int>& timeSeries, int duration) {
int n = timeSeries.size();
int ret = 0;//记录结果
for (int i = 0; i < n - 1; i++)
{
if (timeSeries[i + 1] - timeSeries[i] > duration)
{
ret += duration;//如果说这个右边的比左边的大duration，说明不用重置时间，否则只能加一部分
}
else {
ret += timeSeries[i + 1] - timeSeries[i];
}
}
int i = n - 1;
ret += duration;//单独考虑边界情况
return ret;
}
int main()
{
vector<int> timeSeries = { 1,4 };
int duration = 2;
cout << findPoisonedDuration(timeSeries, duration) << endl;
return 0;
}38.4 总结反思：
这道题基本就是这样的，咱们只需要掌握住题目的意思，根据这个意思去写就可以了。
39. 力扣6 Z字形变化
39.1 题目解析：
这个题目，你要看清楚，这个z是竖着的，不是横着的。
39.2 算法思路：
这道题目就是找出规律才好做，当时作者在那里苦苦的想了半天，硬是没发现规律，结果一看坐标就发现了。
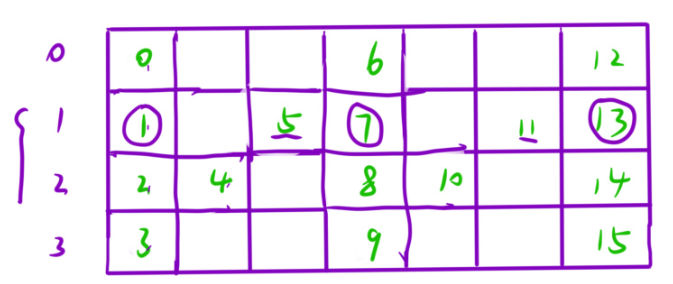
咱们会发现第一行与最后一行都是有公差的，即公差d=2n-2（就是比如0与6之间的元素个数，即2n-2（n是行数））
第一行：0->0+d->0+2d->.....->0+kd
第k行：（k,d-k)->(k+d,d-k+d)->(k+2d,d-k+2d).....
第n-1行 ：n-1->n-1+d->n-1+2d->....->n-1+kd
而中间的，则是2个2个的打包的往后递进。例如1+5=公差d，而1与7之间正好为d。规律也就产生了。
注：以上写的只是在原字符串中进行的移动，所以说它的第一行与最后一行还有中间的，都是要小于n才可以。
还有一种情况需要处理，就是：n=1的时候，d=0.那么这个时候，你要是不处理，就会导致死循环。所以n=1需要当作边界情况处理。
以上只是咱们以4行推出来的，所以要再验证一下其他的才具有说服力：
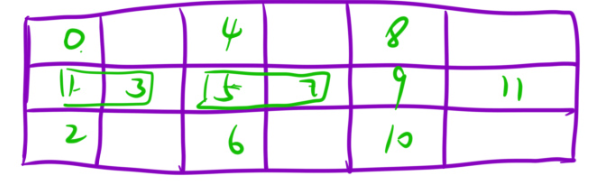
这个是3行，公差就是2n-2=4，第一行与最后一行均符合，中间的也是2个2个的进行打包，也是可以的。
39.3 代码演示：
cpp
string convert(string s, int numRows) {
string ret;//这个用来存储结果
int n = s.size();
int d = 2 * numRows - 2;//算出来公差
if (numRows == 1) return s;//处理边界情况
//1.先处理第一行
for (int i = 0; i < n; i += d)
{
ret += s[i];
}
//2.处理中间的行数
for (int i = 1; i < numRows - 1; i++)//先得是行数的移动
{
for (int j = i, k = d - j; j < n || k < n; j += d, k += d)//这里j或者k，可能j越界了，i还没有，所以要填或者
{
if (j < n) ret += s[j];
if (k < n) ret += s[k];//因为进入到这里的是j越界了或者k越界了，所以还得检测一下才可以加，否则就数组越界了
}
}
//3.处理最后一行
for (int i = numRows - 1; i < n; i += d)
{
ret += s[i];
}
return ret;
}
int main()
{
string s("PAYPALISHIRING");
int numRows = 3;
cout << convert(s, numRows) << endl;
return 0;
}39.4 总结反思：
本道题就是你要是找不出规律，那很难做出来。你要是想不出来看下标，硬做，其实还是挺难的。
40. 力扣 38 外观数列
41.1 题目解析：
题目得好好的读一下，就是你得明白什么意思：
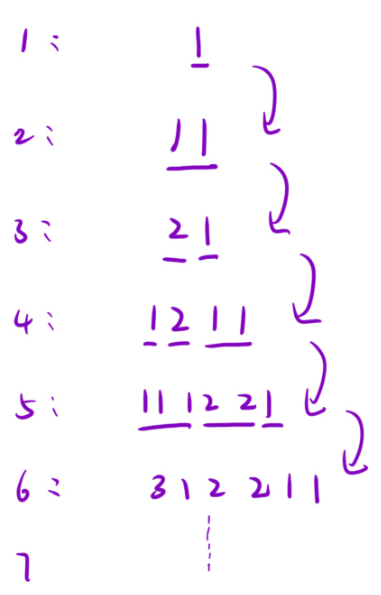
第四个对于第三个进行翻转就是1个2，1个1，就是1211
第五个对于第四个翻转就是：1个1，1个2，2个1，即111221
...................
41.2 算法思路：
咱们这道题目需要用到模拟加上双指针算法才可以解决。
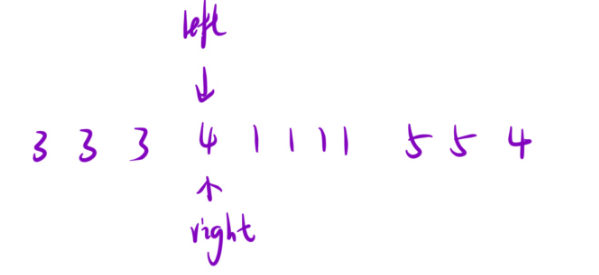
left与right一开始都是在下标为0的位置，right先开始移动，找到与left相同的元素就往右加加，直到遇到与left不同的元素的时候停下，记录一下right与left中间相同元素的数量（此时的元素就是left所指向的位置）。一般的左闭右闭，咱们使用right-left+1.但是这里是右开区间，所以要减去1，那么就是count=right-left。
一直往后移动，直到right越界了这个字符串为止。
所以，咱们应该可以知道，最外层应该是执行了多少次翻转，之后里面才是对与left，right循环的for循环，最里面才是关于寻找count的循环（只要是执行多次相同步骤的，就得写循环）。就是right++（但这个right++，只管一次left，left也得移动，所以才在外层加上一个for循环，以便于控制left的移动）。
41.3 代码演示：
cpp
string countAndSay(int n) {
string ret = "1";//定义一个ret去接收结果。并且这个得初始化为1，因为一开始就是从1开始的
for (int i = 1; i < n; i++)//执行n-1次翻转
{
string tmp;//用来暂时存储字符串
int len = ret.size();//这个是right必须得小于len才可以，因为ret才是那个字符串
for (int left = 0, right = 0; right < len;)
{
while (right < len && ret[right] == ret[left]) right++;//还得防止right越界。注意，这里是个循环
tmp += to_string(right - left) + ret[left];//这个是将有几个1转化为字符串，并且要加上1，即left
left = right;
}
ret = tmp;
}
return ret;
}
int main()
{
int n = 4;
cout << countAndSay(n) << endl;
return 0;
}41.4 总结反思：
本题就是得灵活的结合前面的只是才可以解决。
42. 力扣 1419 数青蛙
42.1 题目解析：
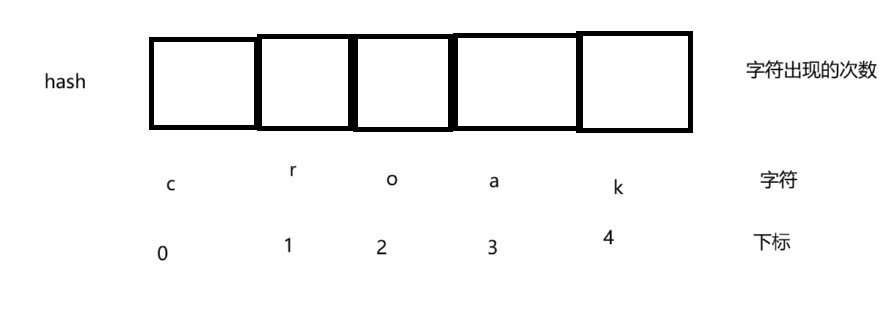
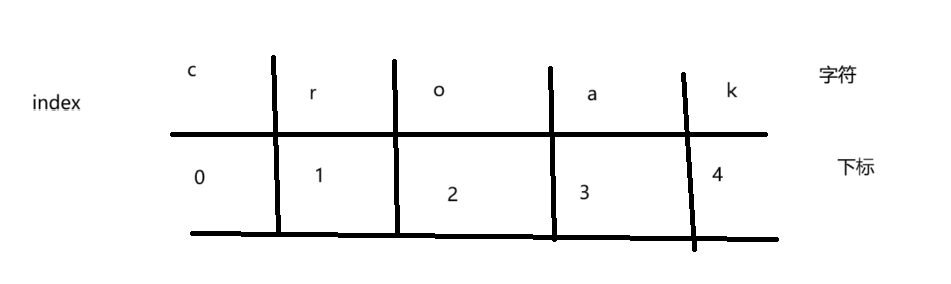
本题是作者今天做的题目里面较复杂的，因为这个模拟算法比较难想。就是如何模拟的比较难想。这个题就是你的每一个c,r,o,a,k都必须得有对应的c,r,o,a，k与之对应，否则就是多余的，多余的就是错的。
42.2 算法思路：
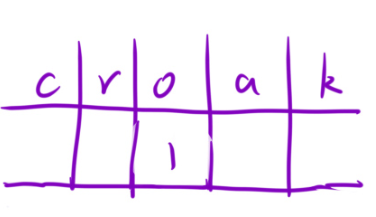
1.从前往后遍历：遇到了C：则C+1,若是遇到了遇到r，看前驱字符，前驱字符若是存在，则前驱字符个数减减，当前字符个数加加。
.............
直到k，开始下一个。
所以C:找最后在一个字符是否在哈希表中存在。若存在，则说明可以把这个青蛙搬过来用（因为它让求的是最小的数目，所以肯定得让利用最大化).若不存在，当前字符(C)++。
而对于r，o，a，k->找前驱字符(r前驱为c，o前驱为r，a前驱为o，k前驱为a）。是否在哈希表中存在过，若是存在过，前驱个数减减，当前字符个数减减。若是不存在，返回-1即可（因为没有对应的前驱与之匹配，说明这个字符是多余的，多余的就是错的，返回-1）。
大家仔细的理解一下，会发现，这个算法还是挺好的，基本做到了每一个字符都是一一对应对应的croak。这样的话，就可以看出来是否croak有多余，是否有顺序。
最后还得判断一下，k之前的字符个数必须为0，否则返回-1（否则就是多余的，多余的肯定返回-1）。
最后这些都完成了，返回k，这个里面的字符的个数。即hash[n-1]
42.3 代码演示：
cpp
int minNumberOfFrogs(string croakOfFrogs)
{
string t = "croak";
int n = t.size();
vector<int> hash(n); // ⽤数组来模拟哈希表
unordered_map<char, int> index; //[x, x这个字符对应的下标]
for (int i = 0; i < n; i++)//这个就是创建了一个哈希表，表中存储字符，表的下方存储字符对应的下标
//目的就是可以通过下标快速的找到那个字符
index[t[i]] = i;
for (auto ch : croakOfFrogs)//这个才是本题的最主要的循环
{
if (ch == 'c')
{
if (hash[n - 1] != 0) hash[n - 1]--;//第一次的话，这个hash[n-1]一定是0，但是第二次就好多了
hash[0]++;
}
else
{
int i = index[ch];//此时下标就派上用场了
if (hash[i - 1] == 0) return -1;
hash[i - 1]--; hash[i]++;
}
}
for (int i = 0; i < n - 1; i++)
if (hash[i] != 0)
return -1;//保证哈希表中k这个字符前面的字符的个数必须为0，否则就是多出了字符，就是错的
return hash[n - 1];//最后这些都完成了，返回哈希表中k这个字符的个数
}
int main()
{
string croakOfFrogs("croakcroa");
cout << minNumberOfFrogs(croakOfFrogs) << endl;
return 0;
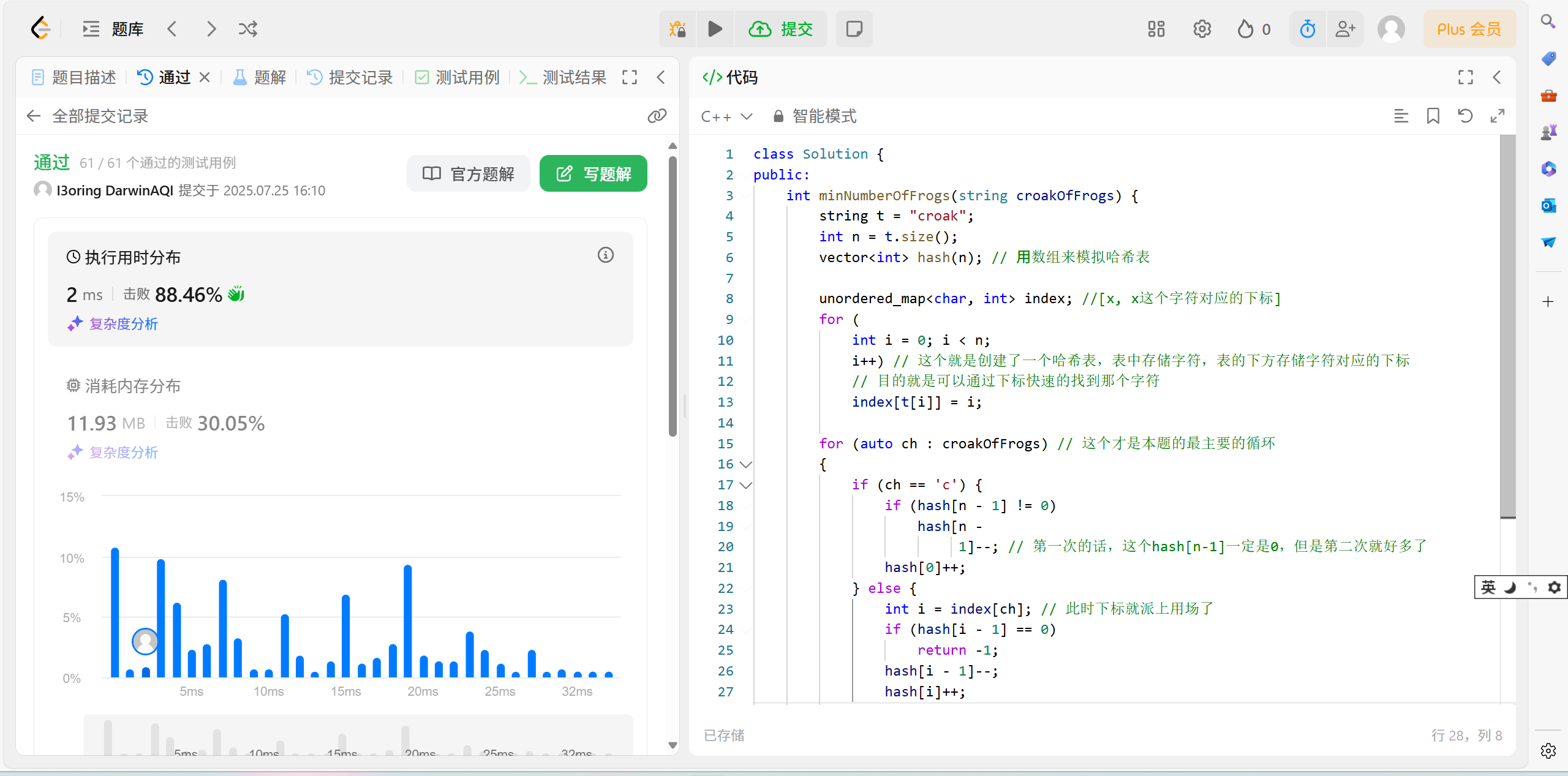
}这个里面的数组比较多，为了防止大家搞晕，我画了几幅图，便于大家理解：
42.4 总结反思：
这道题目还是很考验大家的算法能力的，以及代码的实现能力。