链接:P1144 最短路计数 - 洛谷
题目:
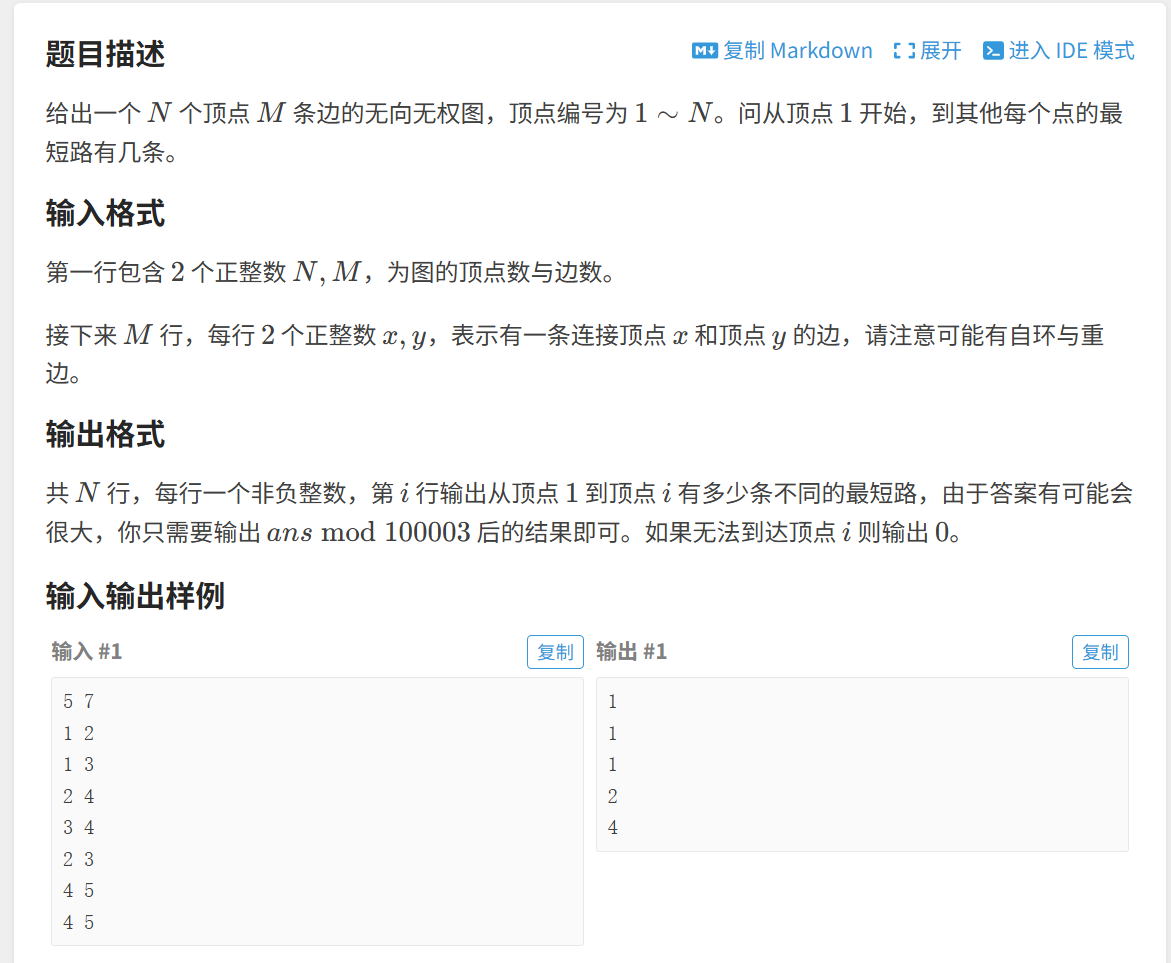
思路:
统计答案比较细节
题目很简单,我们只需要先求出每个点的最短距离,然后用一次记忆化搜索即可
具体的,先使用 SPFA 求出点 1 到 每个点 的最短距离,然后我们采取记忆化搜索,对于点 1,其答案初始化为 1,对于所有子节点,我们利用记忆化搜索枚举答案,对于一个点的子节点 u,如果满足 dis[u] = dis[fa] - 1,说明我们的 fa 可以从 u 转移过来,此时继续递归 u 即可
由于这一题是无权图,所以所有边权为 1 即可
代码:
cpp
#include <iostream>
#include <algorithm>
#include<cstring>
#include <iomanip>
#include<cctype>
#include<string>
#include <set>
#include <vector>
#include <cmath>
#include <queue>
#include <unordered_set>
#include <map>
#include <unordered_map>
#include <stack>
#include <utility>
#include <array>
#include <tuple>
using namespace std;
#define int long long
#define yes cout << "YES" << endl
#define no cout << "NO" << endl
const int N = 1e6 + 5;
const int MOD = 100003;
int n, m;
int dis[N];
int vis[N];
int dp[N];
vector<vector<int>> g(N);
int dfs(int fa)
{
if (dp[fa])
{
return dp[fa];
}
for(auto & to : g[fa])
{
if (dis[to] == dis[fa] - 1)
{
dp[fa] = (dp[fa] + dfs(to)) % MOD;
}
}
return dp[fa];
}
void solve()
{
cin >> n >> m;
for (int i = 1; i <= n; i++)
{
dis[i] = 1e18;
}
for (int i = 0; i < m; i++)
{
int u, v;
cin >> u >> v;
g[u].push_back(v);
g[v].push_back(u);
}
queue<int> q;
dis[1] = 0;
q.push(1);
vis[1] = 1;
while (!q.empty())
{
auto t = q.front();
q.pop();
vis[t] = 0;
for (auto & to : g[t])
{
if (dis[to] > dis[t] + 1)
{
dis[to] = dis[t] + 1;
if (!vis[to])
{
vis[to] = 1;
q.push(to);
}
}
}
}
dp[1] = 1;
for (int i = 1; i <= n; i++)
{
cout << dfs(i) << endl;
}
}
signed main()
{
cin.tie(0)->sync_with_stdio(false);
int t = 1;
//cin >> t;
while (t--)
{
solve();
}
return 0;
}拓展:
若对于有权图,那么我们则还需要在边上加上 w 这个元素
如:
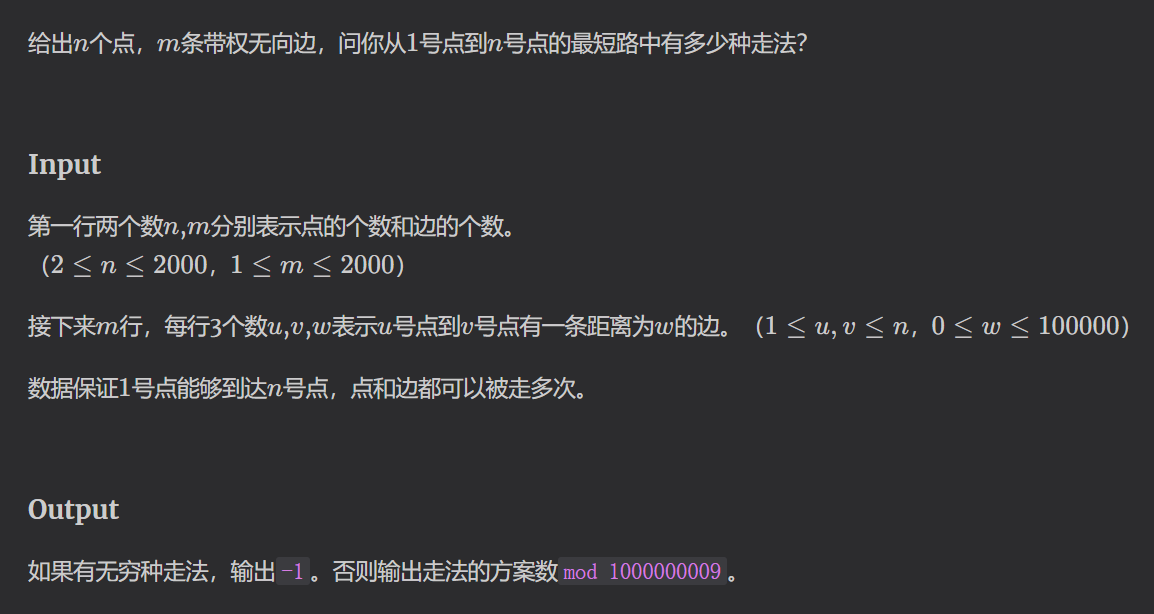
对于这一题我们还是一样的讨论,只不过到了 1 变成了 w,这里我们主要讨论什么时候能无穷多种走法,注意到题目种 w 可能为 0,此时我们可以反复走过这条边来刷步数,即当 1 -> n 的这条路上含有 边权为 0 的边时有无穷多种走法
cpp
#include <iostream>
#include <algorithm>
#include <cstring>
#include <iomanip>
#include <cctype>
#include <string>
#include <set>
#include <vector>
#include <cmath>
#include <queue>
#include <unordered_set>
#include <map>
#include <unordered_map>
#include <stack>
#include <utility>
#include <array>
#include <tuple>
using namespace std;
#define int long long
#define yes cout << "YES" << endl
#define no cout << "NO" << endl
const int N = 1e6 + 5;
const int MOD = 1000000009;
int n, m;
int dis[N];
int vis[N];
int dp[N];
int flag = 0;
vector<vector<pair<int, int>>> g(N);
int dfs(int fa)
{
if (flag)
{
return -1;
}
if (dp[fa])
{
return dp[fa];
}
for (auto &son : g[fa])
{
if (flag)
{
return -1;
}
int to = son.first;
int w = son.second;
if (dis[to] == dis[fa] - w)
{
if (w == 0)
{
flag = 1;
return -1;
}
dp[fa] = (dp[fa] + dfs(to)) % MOD;
}
}
return dp[fa];
}
void solve()
{
cin >> n >> m;
for (int i = 1; i <= n; i++)
{
dis[i] = 1e18;
}
for (int i = 0; i < m; i++)
{
int u, v, w;
cin >> u >> v >> w;
g[u].push_back({v, w});
g[v].push_back({u, w});
}
queue<int> q;
dis[1] = 0;
q.push(1);
vis[1] = 1;
while (!q.empty())
{
auto t = q.front();
q.pop();
vis[t] = 0;
for (auto &son : g[t])
{
int to = son.first;
int w = son.second;
if (dis[to] > dis[t] + w)
{
dis[to] = dis[t] + w;
if (!vis[to])
{
vis[to] = 1;
q.push(to);
}
}
}
}
dp[1] = 1;
// for (int i = 1; i <= n; i++)
// {
// cout << dfs(i) << endl;
// }
int ans = dfs(n);
cout << (!flag ? ans : -1) << endl;
}
signed main()
{
cin.tie(0)->sync_with_stdio(false);
int t = 1;
// cin >> t;
while (t--)
{
solve();
}
return 0;
}