TOPSIS（Technique for Order Preference by Similarity to Ideal Solution ）简介与简单示例

前言

提醒：

文章内容为方便作者自己后日复习与查阅而进行的书写与发布，其中引用内容都会使用链接表明出处（如有侵权问题，请及时联系）。

其中内容多为一次书写，缺少检查与订正，如有问题或其他拓展及意见建议，欢迎评论区讨论交流。
内容由AI辅助生成，仅经笔者审核整理，请甄别食用。

文章目录

前言
TOPSIS方法：多准则决策的几何解析
- - 一、核心步骤与公式（附变量解释）
  - - [1. 输入定义](#1. 输入定义)
    - [2. 步骤1：归一化决策矩阵（消除量纲）](#2. 步骤1：归一化决策矩阵（消除量纲）)
    - [3. 步骤2：加权归一化（融合准则权重）](#3. 步骤2：加权归一化（融合准则权重）)
    - [4. 步骤3：确定理想解（正/负）](#4. 步骤3：确定理想解（正/负）)
    - [5. 步骤4：计算距离（理想解的远近）](#5. 步骤4：计算距离（理想解的远近）)
    - [6. 步骤5：计算贴近度（方案优劣排序）](#6. 步骤5：计算贴近度（方案优劣排序）)
  - 二、关键特点与优势
  - 三、示例解析（简化场景：2方案×2准则）
  - - [1. 归一化（消除量纲）](#1. 归一化（消除量纲）)
    - [2. 加权归一化（融合权重）](#2. 加权归一化（融合权重）)
    - [3. 确定理想解](#3. 确定理想解)
    - [4. 计算距离与贴近度](#4. 计算距离与贴近度)
    - [5. 排序结论](#5. 排序结论)
  - 四、方法对比与适用场景
  - 五、总结
简单示例
- - 代码说明：

TOPSIS方法：多准则决策的几何解析

TOPSIS（Technique for Order Preference by Similarity to Ideal Solution ）由Yoon和Hwang于1981年提出，是经典多准则决策（MCDM）方法。其核心逻辑是：将决策问题映射到 n n n维空间（ n n n为准则数量），通过计算方案与"正理想解""负理想解"的距离，筛选最接近正理想解、最远离负理想解的方案，实现复杂决策的量化排序。

一、核心步骤与公式（附变量解释）

1. 输入定义

决策矩阵 ：设方案数为 m m m、准则数为 n n n，原始矩阵记为 X = ( x i j ) m × n \mathbf{X} = (x_{ij}){m \times n} X=(xij)m×n。其中 x i j x{ij} xij表示第 i i i个方案 在第 j j j个准则下的原始值（如"方案1的成本值" ）。
准则权重 ：记为 W = ( w 1 , w 2 , ... , w n ) \mathbf{W} = (w_1, w_2, \dots, w_n) W=(w1,w2,...,wn)，满足 ∑ j = 1 n w j = 1 \sum_{j=1}^n w_j = 1 ∑j=1nwj=1。 w j w_j wj表示第 j j j个准则的重要性（如"成本准则权重0.3，说明成本占30%决策权重" ）。

2. 步骤1：归一化决策矩阵（消除量纲）

通过向量归一化 统一量纲，公式：
x ˉ i j = x i j ∑ i = 1 m x i j 2 \bar{x}{ij} = \frac{x{ij}}{\sqrt{\sum_{i=1}^m x_{ij}^2}} xˉij=∑i=1mxij2 xij

变量： x ˉ i j \bar{x}_{ij} xˉij是第 i i i个方案 在第 j j j个准则 下的归一化值，输出区间 [ 0 , 1 ] [0,1] [0,1]，解决不同准则单位差异问题（如"成本（元）"与"效率（件/时）"无法直接比较）。

3. 步骤2：加权归一化（融合准则权重）

结合准则权重调整归一化值，公式：
V i j = x ˉ i j × w j V_{ij} = \bar{x}_{ij} \times w_j Vij=xˉij×wj

变量： V i j V_{ij} Vij是第 i i i个方案 在第 j j j个准则下的加权归一化值，体现"准则重要性对方案表现的放大/缩小"（如"高权重准则的方案值，对决策结果影响更强" ）。

4. 步骤3：确定理想解（正/负）

正理想解 A + A^+ A+ ：各准则的最优值，公式：
A j + = { max ⁡ i V i j （准则 j 为最大化目标，如"利润"） min ⁡ i V i j （准则 j 为最小化目标，如"成本"） A_j^+ = \begin{cases} \max_i V_{ij} & \text{（准则 } j \text{ 为最大化目标，如"利润"）} \\ \min_i V_{ij} & \text{（准则 } j \text{ 为最小化目标，如"成本"）} \end{cases} Aj+={maxiVijminiVij（准则 j 为最大化目标，如"利润"）（准则 j 为最小化目标，如"成本"）
- 变量： A j + A_j^+ Aj+是第 j j j个准则下的"最优表现"（如"所有方案中成本最低值" ）。
负理想解 A − A^- A− ：各准则的最劣值，与正理想解相反，公式：
A j − = { min ⁡ i V i j （准则 j 为最大化目标） max ⁡ i V i j （准则 j 为最小化目标） A_j^- = \begin{cases} \min_i V_{ij} & \text{（准则 } j \text{ 为最大化目标）} \\ \max_i V_{ij} & \text{（准则 } j \text{ 为最小化目标）} \end{cases} Aj−={miniVijmaxiVij（准则 j 为最大化目标）（准则 j 为最小化目标）
- 变量： A j − A_j^- Aj−是第 j j j个准则下的"最劣表现"（如"所有方案中成本最高值" ）。

5. 步骤4：计算距离（理想解的远近）

到正理想解的距离 d i + d_i^+ di+ ：
d i + = ∑ j = 1 n ( V i j − A j + ) 2 d_i^+ = \sqrt{\sum_{j=1}^n (V_{ij} - A_j^+)^2} di+=j=1∑n(Vij−Aj+)2
- 变量： d i + d_i^+ di+是第 i i i个方案到正理想解的欧氏距离，距离越大，方案离"最优表现"越远。
到负理想解的距离 d i − d_i^- di− ：
d i − = ∑ j = 1 n ( V i j − A j − ) 2 d_i^- = \sqrt{\sum_{j=1}^n (V_{ij} - A_j^-)^2} di−=j=1∑n(Vij−Aj−)2
- 变量： d i − d_i^- di−是第 i i i个方案到负理想解的欧氏距离，距离越大，方案离"最劣表现"越远。

6. 步骤5：计算贴近度（方案优劣排序）

贴近度反映方案与正理想解的相对接近程度，公式：
C i = d i − d i + + d i − C_i = \frac{d_i^-}{d_i^+ + d_i^-} Ci=di++di−di−

变量： C i ∈ [ 0 , 1 ] C_i \in [0,1] Ci∈[0,1]，值越大表示第 i i i个方案 越接近正理想解、越远离负理想解，方案越优。最终按 C i C_i Ci降序排序，确定方案优先级。

二、关键特点与优势

几何直观性 ：将决策映射到 n n n维空间，用"距离理想解的远近"排序，逻辑清晰（如二维场景可类比平面上点与"最优/最劣点"的距离比较）。
混合准则支持 ：兼容最大化、最小化目标（仅需在确定 A + A^+ A+、 A − A^- A−时区分准则类型），覆盖"利润最大化+成本最小化"等复杂场景。
计算简洁性：基于欧氏距离和加权归一化，流程明确，手工或编程均可快速实现。

三、示例解析（简化场景：2方案×2准则）

假设场景：2个方案（桂林、黄山）、2个准则（景色：最大化，权重0.6；费用：最小化，权重0.4 ），原始矩阵 X = [ 9 7 8 6 ] \mathbf{X} = \begin{bmatrix} 9 & 7 \\ 8 & 6 \end{bmatrix} X=[9876]（桂林：景色9、费用7；黄山：景色8、费用6 ）。

1. 归一化（消除量纲）

x ˉ 11 = 9 9 2 + 8 2 ≈ 0.676 , x ˉ 12 = 7 7 2 + 6 2 ≈ 0.714 x ˉ 21 = 8 9 2 + 8 2 ≈ 0.606 , x ˉ 22 = 6 7 2 + 6 2 ≈ 0.618 \bar{x}{11} = \frac{9}{\sqrt{9^2+8^2}} \approx 0.676,\ \bar{x}{12} = \frac{7}{\sqrt{7^2+6^2}} \approx 0.714 \\ \bar{x}{21} = \frac{8}{\sqrt{9^2+8^2}} \approx 0.606,\ \bar{x}{22} = \frac{6}{\sqrt{7^2+6^2}} \approx 0.618 xˉ11=92+82 9≈0.676, xˉ12=72+62 7≈0.714xˉ21=92+82 8≈0.606, xˉ22=72+62 6≈0.618

2. 加权归一化（融合权重）

V 11 = 0.676 × 0.6 ≈ 0.406 , V 12 = 0.714 × 0.4 ≈ 0.286 V 21 = 0.606 × 0.6 ≈ 0.364 , V 22 = 0.618 × 0.4 ≈ 0.247 V_{11} = 0.676×0.6 \approx 0.406,\ V_{12} = 0.714×0.4 \approx 0.286 \\ V_{21} = 0.606×0.6 \approx 0.364,\ V_{22} = 0.618×0.4 \approx 0.247 V11=0.676×0.6≈0.406, V12=0.714×0.4≈0.286V21=0.606×0.6≈0.364, V22=0.618×0.4≈0.247

3. 确定理想解

景色（最大化）： A 1 + = 0.406 A_1^+ = 0.406 A1+=0.406（桂林）、 A 1 − = 0.364 A_1^- = 0.364 A1−=0.364（黄山）
费用（最小化）： A 2 + = 0.247 A_2^+ = 0.247 A2+=0.247（黄山）、 A 2 − = 0.286 A_2^- = 0.286 A2−=0.286（桂林）

4. 计算距离与贴近度

桂林： d 1 + ≈ 0.039 d_1^+ \approx 0.039 d1+≈0.039（到正理想解距离）、 d 1 − ≈ 0.042 d_1^- \approx 0.042 d1−≈0.042（到负理想解距离）， C 1 ≈ 0.518 C_1 \approx 0.518 C1≈0.518
黄山： d 2 + ≈ 0.042 d_2^+ \approx 0.042 d2+≈0.042（到正理想解距离）、 d 2 − ≈ 0.039 d_2^- \approx 0.039 d2−≈0.039（到负理想解距离）， C 2 ≈ 0.482 C_2 \approx 0.482 C2≈0.482

5. 排序结论

因 C 1 > C 2 C_1 > C_2 C1>C2，桂林更接近正理想解，为更优方案。

四、方法对比与适用场景

方法	核心逻辑	适用场景	局限性
TOPSIS	距离理想解的相对接近度	数据分布均匀、混合准则场景	对异常值敏感
VIKOR	妥协解（平衡群体效用与遗憾）	需多方协商的复杂决策	计算稍复杂
AHP	成对比较确定权重	权重确定阶段	主观依赖强
COPRAS	区分准则类型的相对显著性	成本敏感型决策	最小化准则影响突出

五、总结

TOPSIS 以几何直观性、混合准则兼容性、计算简洁性 为核心优势，适合工程评估、项目优选等场景。其本质是将定性决策转化为"距离比较"的定量问题，通过 C i C_i Ci实现方案排序。需注意：若数据存在异常值（如极端大/小值），需预处理（如离群值修正），否则可能影响结果可靠性。

简单示例

下面是一个使用TOPSIS优化方法的MATLAB实现，包含完整计算流程和可视化功能。这个示例解决了一个经典的"供应商选择"问题，通过TOPSIS方法在多个准则下对备选方案进行排序和选择。

matlab 复制代码

%% TOPSIS（Technique for Order Preference by Similarity to Ideal Solution）优化方法示例
clear; clc; close all;

%% 1. 定义问题数据
% 备选方案（供应商）
alternatives = {'供应商A', '供应商B', '供应商C', '供应商D', '供应商E'};
num_alternatives = length(alternatives);

% 评价准则
criteria = {'价格', '质量', '交货期', '服务水平', '环保性'};
num_criteria = length(criteria);

% 准则权重（可通过AHP等方法确定）
weights = [0.25, 0.20, 0.15, 0.20, 0.20];

% 决策矩阵（方案在各准则下的表现）
% 注："价格"为最小化准则，其余为最大化准则
decision_matrix = [
    80, 7, 9, 8, 7;    % 供应商A
    90, 8, 7, 9, 8;    % 供应商B
    70, 9, 6, 7, 9;    % 供应商C
    60, 6, 8, 6, 6;    % 供应商D
    85, 7, 10, 8, 8;   % 供应商E
];

% 标记准则类型（1=最大化，0=最小化）
criteria_type = [0, 1, 1, 1, 1];

%% 2. TOPSIS计算流程
% 步骤1：归一化决策矩阵（向量归一化）
normalized_matrix = zeros(size(decision_matrix));
for j = 1:num_criteria
    if criteria_type(j) == 1  % 最大化准则
        normalized_matrix(:,j) = decision_matrix(:,j) / norm(decision_matrix(:,j));
    else  % 最小化准则
        normalized_matrix(:,j) = min(decision_matrix(:,j)) ./ decision_matrix(:,j);
        normalized_matrix(:,j) = normalized_matrix(:,j) / norm(normalized_matrix(:,j));
    end
end

% 步骤2：加权归一化矩阵
weighted_matrix = normalized_matrix .* repmat(weights, num_alternatives, 1);

% 步骤3：确定正理想解和负理想解
positive_ideal = zeros(1, num_criteria);
negative_ideal = zeros(1, num_criteria);
for j = 1:num_criteria
    if criteria_type(j) == 1  % 最大化准则
        positive_ideal(j) = max(weighted_matrix(:,j));
        negative_ideal(j) = min(weighted_matrix(:,j));
    else  % 最小化准则
        positive_ideal(j) = min(weighted_matrix(:,j));
        negative_ideal(j) = max(weighted_matrix(:,j));
    end
end

% 步骤4：计算到正理想解和负理想解的距离
d_plus = zeros(num_alternatives, 1);
d_minus = zeros(num_alternatives, 1);
for i = 1:num_alternatives
    d_plus(i) = norm(weighted_matrix(i,:) - positive_ideal);
    d_minus(i) = norm(weighted_matrix(i,:) - negative_ideal);
end

% 步骤5：计算相对贴近度
relative_closeness = d_minus ./ (d_plus + d_minus);

% 步骤6：排序
[closeness_sorted, sort_idx] = sort(relative_closeness, 'descend');

%% 3. 可视化结果
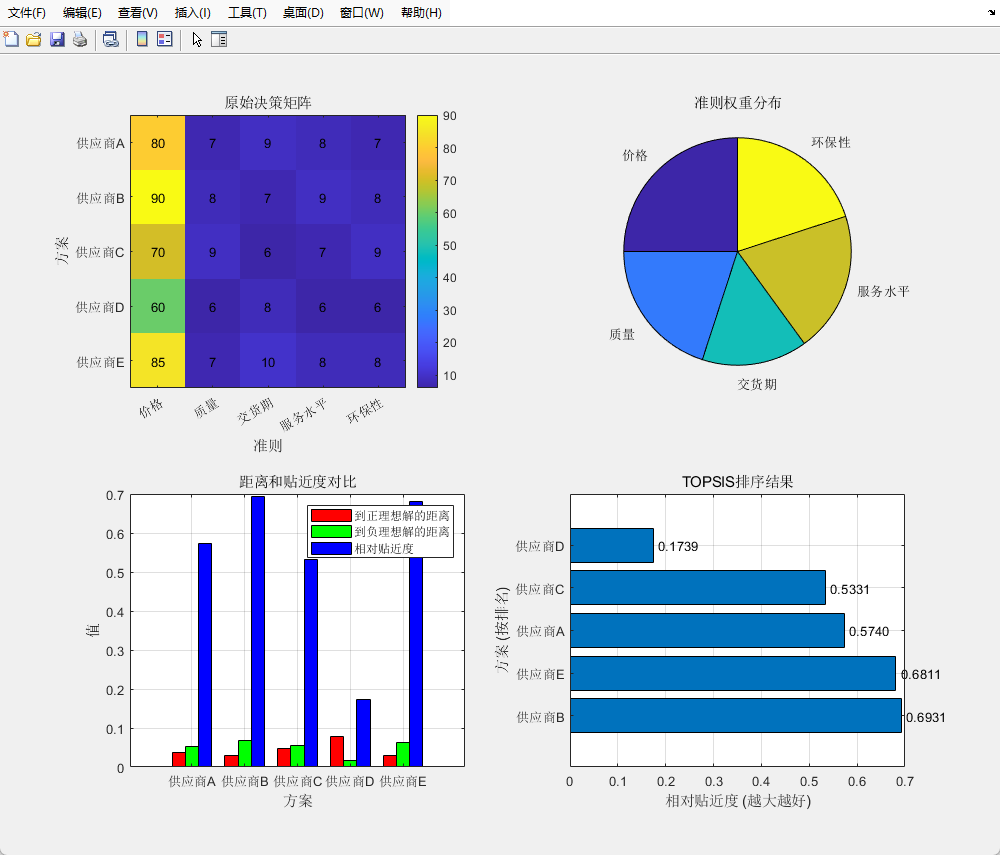
% 3.1 决策矩阵热图
figure('Position', [100, 100, 1000, 800]);
subplot(2, 2, 1);
imagesc(decision_matrix);
title('原始决策矩阵');
xlabel('准则');
ylabel('方案');
set(gca, 'XTick', 1:num_criteria, 'XTickLabel', criteria);
set(gca, 'YTick', 1:num_alternatives, 'YTickLabel', alternatives);
colorbar;
for i = 1:num_alternatives
    for j = 1:num_criteria
        text(j, i, num2str(decision_matrix(i,j)), 'HorizontalAlignment', 'center', 'FontSize', 10);
    end
end

% 3.2 准则权重饼图
subplot(2, 2, 2);
pie(weights, criteria);
title('准则权重分布');

% 3.3 距离和贴近度对比图
subplot(2, 2, 3);
bar_width = 0.25;
x = 1:num_alternatives;
bar(x - bar_width, d_plus, bar_width, 'r', 'DisplayName', '到正理想解的距离');
hold on;
bar(x, d_minus, bar_width, 'g', 'DisplayName', '到负理想解的距离');
bar(x + bar_width, relative_closeness, bar_width, 'b', 'DisplayName', '相对贴近度');
hold off;
title('距离和贴近度对比');
xlabel('方案');
ylabel('值');
set(gca, 'XTick', 1:num_alternatives, 'XTickLabel', alternatives);
legend;
grid on;

% 3.4 TOPSIS排序结果
subplot(2, 2, 4);
barh(1:num_alternatives, closeness_sorted);
title('TOPSIS排序结果');
xlabel('相对贴近度 (越大越好)');
ylabel('方案 (按排名)');
set(gca, 'YTick', 1:num_alternatives, 'YTickLabel', alternatives(sort_idx));
grid on;

% 添加标签显示具体贴近度值
for i = 1:num_alternatives
    text(closeness_sorted(i)+0.01, i, sprintf('%.4f', closeness_sorted(i)), 'HorizontalAlignment', 'left', 'VerticalAlignment', 'middle');
end

%% 4. 输出结果
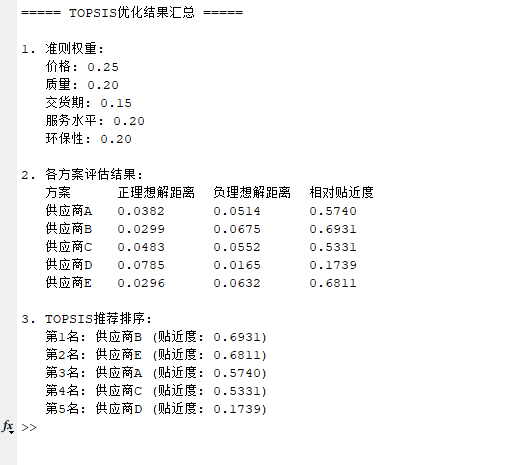
fprintf('\n===== TOPSIS优化结果汇总 =====\n');
fprintf('\n1. 准则权重:\n');
for i = 1:num_criteria
    fprintf('   %s: %.2f\n', criteria{i}, weights(i));
end

fprintf('\n2. 各方案评估结果:\n');
fprintf('   方案\t\t正理想解距离\t负理想解距离\t相对贴近度\n');
for i = 1:num_alternatives
    fprintf('   %s\t%.4f\t\t%.4f\t\t%.4f\n', alternatives{i}, d_plus(i), d_minus(i), relative_closeness(i));
end

fprintf('\n3. TOPSIS推荐排序:\n');
for i = 1:num_alternatives
    fprintf('   第%d名: %s (贴近度: %.4f)\n', i, alternatives{sort_idx(i)}, closeness_sorted(i));
end

代码说明：

问题定义：
- 5个备选方案（供应商A-E）
- 5个评价准则：价格、质量、交货期、服务水平、环保性
- 准则权重：通过专家判断或AHP方法预先确定
- 准则类型："价格"为最小化准则，其余为最大化准则
TOPSIS计算流程：
- 归一化处理：针对不同类型准则采用不同归一化方法
- 加权处理：结合准则权重调整归一化后的决策矩阵
- 确定理想解：分别计算正理想解和负理想解
- 计算距离：计算各方案到正理想解和负理想解的欧氏距离
- 计算相对贴近度：综合距离指标得到最终评分
- 排序：按相对贴近度降序排列
可视化功能：
- 决策矩阵热图：直观展示原始数据
- 准则权重饼图：显示各准则重要性分布
- 距离和贴近度对比图：横向比较各方案在不同指标下的表现
- TOPSIS排序结果：按相对贴近度从高到低展示
结果输出：
- 详细列出各方案的距离指标和相对贴近度
- 给出推荐排序结果

运行结果