DPO学习笔记
- [1 原理](#1 原理)
-
- [1.0 名词](#1.0 名词)
- [1.1 preference model](#1.1 preference model)
- [1.2 RLHF](#1.2 RLHF)
- [1.3 从RLHF到DPO](#1.3 从RLHF到DPO)
-
- A.解的最优形式
- [B. DPO下参数估计](#B. DPO下参数估计)
- [C. DPO下梯度更新](#C. DPO下梯度更新)
- [D. DPO训练的稳定性](#D. DPO训练的稳定性)
- [2 源代码](#2 源代码)
-
- [2.1 数据集构成](#2.1 数据集构成)
- [2.2 计算log prob](#2.2 计算log prob)
- [2.3 DPO loss](#2.3 DPO loss)
1 原理
1.0 名词
- preference model:对人类偏好进行建模,这个"model"不是DL model
- policy model:最终要训练得到的LLM π θ \pi_\theta πθ
- reward model:用来评价LLM生成的结果有多符合人类偏好
1.1 preference model
- 是一种者范式、定义,是用来预测人类对不同输出项之间相对偏好概率的模型,例如,在比较两个响应时,偏好模型可以估计出"响应A比响应B更受欢迎"的概率
- DPO中使用的是Bradley--Terry 模型来定义偏好的概率形式,给定2个选项 y w y_w yw和 y l y_l yl,Bradley--Terry 定义的的 y w y_w yw比 y l y_l yl好的概率为
p ( y w ≥ y l ) = e x p ( θ w ) e x p ( θ w ) + e x p ( θ l ) p(y_w \ge y_l)=\frac{exp(\theta_w)}{exp(\theta_w)+exp(\theta_l)} p(yw≥yl)=exp(θw)+exp(θl)exp(θw)
1.2 RLHF
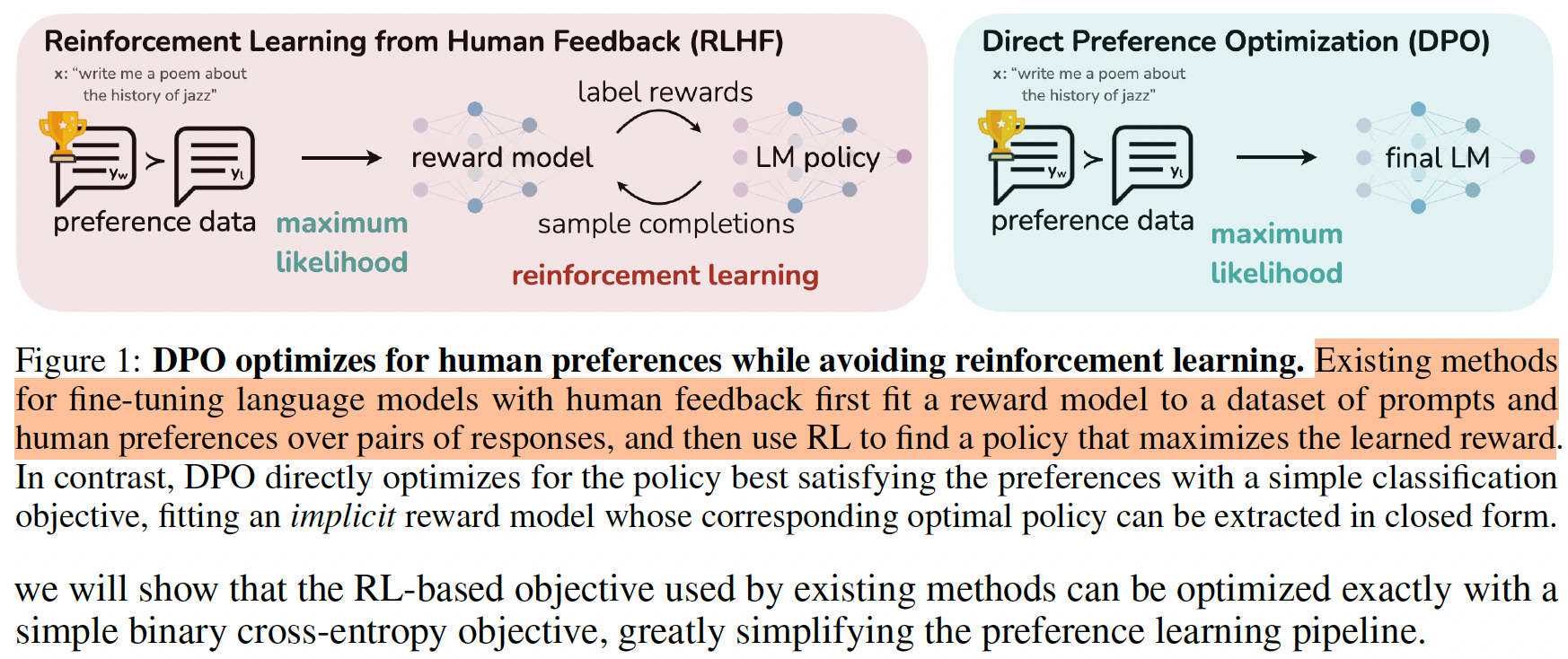
RLHF需要使用人标注的偏好数据对,先训练一个reward model,然后再让reward model和LLM做强化学习
【1】SFT训练LLM: 使用目标任务的训练数据训练得到的模型记为 π S F T \pi^{SFT} πSFT
【2】训练reward model: 使用目标任务的另一份数据 x x x输入 π S F T \pi^{SFT} πSFT,每份数据得到2个输出,记为 ( y 1 , y 2 ) ∼ π S F T ( y ∣ x ) (y_1,y_2) \sim \pi^{SFT}(y \mid x) (y1,y2)∼πSFT(y∣x)。这些成对的数据给到人工标注者,进行偏好标注, ( y 1 , y 2 ) (y_1,y_2) (y1,y2)里面人工觉得回答的好的数据为 y w y_w yw,觉得回答的不好的数据为 y l y_l yl,得到的数据集为 D = { x i , y w i , y l i } i = 1 N \mathcal{D}=\{x^{i},y^i_w,y^i_l\}^N_{i=1} D={xi,ywi,yli}i=1N。假设这种偏好产生自一个隐藏的奖励模型 r ∗ ( y , x ) r^*(y,x) r∗(y,x),当使用Bradley-Terry模型来建模,人类偏好 p ∗ p^* p∗的分布可以表示为
p ∗ ( y w ≻ y l ∣ x ) = e x p ( r ∗ ( x . y 1 ) ) e x p ( r ∗ ( x . y 1 ) ) + e x p ( r ∗ ( x . y 2 ) ) p^*(y_w \succ y_l \mid x)=\frac{exp(r^*(x.y_1))}{exp(r^*(x.y_1))+exp(r^*(x.y_2))} p∗(yw≻yl∣x)=exp(r∗(x.y1))+exp(r∗(x.y2))exp(r∗(x.y1))
可以形式化奖励模型参数为 r ϕ ( x , y ) r_\phi(x,y) rϕ(x,y)并且使用极大似然估计在数据集 D \mathcal{D} D上估计参数,建模为二分类问题,损失函数可以为(也可以是其他形式,相减比较符合认知):
L R ( r ϕ , D ) = − E ( x , y w , y l ) ∼ D [ l o g σ ( r ϕ ( x , y w ) − r ϕ ( x , y l ) ) ] \mathcal{L}R(r\phi,\mathcal{D})=-\mathbb{E}{(x,y_w,y_l)\sim\mathcal{D}}[log \sigma(r\phi(x,y_w)-r_\phi(x,y_l))] LR(rϕ,D)=−E(x,yw,yl)∼D[logσ(rϕ(x,yw)−rϕ(x,yl))]
【3】RL微调: 在RL阶段,优化目标带有KL约束
max π θ E x ∼ D , y ∼ π θ ( y ∣ x ) [ r ϕ ( x , y ) − β D K L [ π θ ( y ∣ x ) ∥ π r e f ( y ∣ x ) ] ] \max_{\pi_{\theta}}\mathbb{E}{x \sim \mathcal{D},y \sim \pi{\theta}(y \mid x)}[r_\phi(x,y)-\beta\mathbb{D}{KL}[\pi{\theta}(y \mid x)\parallel \pi_{ref}(y \mid x)]] πθmaxEx∼D,y∼πθ(y∣x)[rϕ(x,y)−βDKL[πθ(y∣x)∥πref(y∣x)]]
1.3 从RLHF到DPO
A.解的最优形式
首先,根据RL优化目标的形式,奖励函数为 r r r,最优的策略 π \pi π的形式为
π r ( y ∣ x ) ) = 1 Z ( x ) π r e f ( y ∣ x ) e x p ( 1 β r ( x , y ) ) \pi_r(y \mid x))=\frac{1}{Z(x)}\pi_{ref}(y \mid x) exp(\frac{1}{\beta}r(x,y)) πr(y∣x))=Z(x)1πref(y∣x)exp(β1r(x,y))
其中 Z ( x ) = ∑ y π r e f ( y ∣ x ) e x p ( 1 β r ( x , y ) ) Z(x)=\sum_{y}\pi_{ref}(y \mid x) exp(\frac{1}{\beta}r(x,y)) Z(x)=∑yπref(y∣x)exp(β1r(x,y))。之所以能得到这个形式在原论文的附录中有推导

里面的第3步到第4步是因为可以引入 Z ( x ) Z(x) Z(x)构造一个新的概率分布, Z ( x ) Z(x) Z(x)是归一化因子,保证 π ~ ( y ∣ x ) \tilde{\pi} (y \mid x) π~(y∣x)是有效的概率分布:
π ~ ( y ∣ x ) = 1 Z ( x ) π r e f e x p ( 1 β r ( x , y ) ) \tilde{\pi} (y \mid x)=\frac{1}{Z(x)}\pi_{ref}exp(\frac{1}{\beta}r(x,y)) π~(y∣x)=Z(x)1πrefexp(β1r(x,y))
这样,原来的式子
l o g π ( y ∣ x ) π r e f ( y ∣ x ) = l o g π ( y ∣ x ) − π r e f ( y ∣ x ) − l o g [ e x p ( 1 β r ( x , y ) ) ] = l o g π ( y ∣ x ) π ~ ( y ∣ x ) − l o g Z ( x ) log \frac{\pi(y \mid x)}{\pi_{ref}(y \mid x)} =log\pi(y \mid x)-\pi_{ref}(y \mid x) - log[exp(\frac{1}{\beta}r(x,y))] \\ =log \frac{\pi(y \mid x)}{\tilde{\pi}_(y \mid x)} - log Z(x) logπref(y∣x)π(y∣x)=logπ(y∣x)−πref(y∣x)−log[exp(β1r(x,y))]=logπ~(y∣x)π(y∣x)−logZ(x)
又因 π \pi π的形式只需要满足是合法的概率分布就可以,因此形式上可以替换,以及 Z ( x ) Z(x) Z(x)不是 y y y的函数,所以期望写进去不会对 l o g Z ( x ) log Z(x) logZ(x)有影响,得到了最优策略下,策略函数的形式(给定 x x x的情况下输出 y y y的概率 / 在给定状态 S S S的情况下,下一个时间的进入状态 S ′ S' S′的概率)
π ∗ ( y ∣ x ) = 1 Z ( x ) π r e f ( y ∣ x ) e x p ( 1 β r ( x , y ) ) \pi^*(y \mid x)= \frac{1}{Z(x)}\pi_{ref}(y \mid x) exp(\frac{1}{\beta} r(x,y)) π∗(y∣x)=Z(x)1πref(y∣x)exp(β1r(x,y))

B. DPO下参数估计
- 即使得到了最优策略 π r \pi_r πr的形式,并且即使把里面的 r ( x , y ) r(x,y) r(x,y)用MLE估计的 r r r来替换,里面也有一个 Z ( x ) Z(x) Z(x)需要估计, Z ( x ) Z(x) Z(x)的计算是很复杂的,里面的"状态"或者说词表 y y y很大的情况下开销大
- 但是可以进一步把式子整理一下,重新表示一下reward函数
r ( x , y ) = β l o g π r ( y ∣ x ) π r e f ( y ∣ x ) + β l o g Z ( x ) r(x,y)=\beta log \frac{\pi_r(y \mid x)}{\pi_{ref}(y \mid x)}+ \beta log Z(x) r(x,y)=βlogπref(y∣x)πr(y∣x)+βlogZ(x) - 带入原始的Bradley-Terry的式子,会发现,最后衡量偏好的函数里面,没有reward function Z ( x ) Z(x) Z(x)这一项需要计算了抵消掉了

- 所以DPO的目标是提升 y w ≻ y l y_w \succ y_l yw≻yl的概率,损失函数的形式为
L D P O ( π θ ; π r e f ) = − E ( x , y w , w l ) ∼ D [ l o g σ ( β l o g π θ ( y w ∣ x ) π r e f ( y w ∣ x ) − β l o g π θ ( y l ∣ x ) π r e f ( y l ∣ x ) ) ] \mathcal{L}{DPO}(\pi\theta;\pi_{ref}) = -\mathbb{E}{(x,y_w,w_l)\sim \mathcal{D}}[log \sigma(\beta log \frac{\pi\theta(y_w \mid x)}{\pi_{ref}(y_w \mid x)} - \beta log \frac{\pi_\theta(y_l \mid x)}{\pi_{ref}(y_l \mid x)}) ] LDPO(πθ;πref)=−E(x,yw,wl)∼D[logσ(βlogπref(yw∣x)πθ(yw∣x)−βlogπref(yl∣x)πθ(yl∣x))]
C. DPO下梯度更新

- 和人类偏好差异越大的,前面的系数越大
D. DPO训练的稳定性

- 第二项为归一化项是常数是因为对当前 x x x,遍历了所有的 y y y
- 减少极端值的影响:通过指数加权平均,极端值的影响会被削弱,从而使得奖励函数更加平滑
- 稳定梯度估计:由于奖励函数变得更加平滑,策略梯度的估计也会更加稳定,方差会显著减小
2 源代码
RLAIF-V:https://github.com/RLHF-V/RLAIF-V/tree/main
2.1 数据集构成
- chose------人类偏好的回答
- rejected------SFT阶段的模型回答
- ref_win_logp------人类偏好回答的所有token的log_probability之和
- ref_rej_logp------模型回答的的所有token的log_probability之和
- ref_win_avg_logp------人类偏好回答的所有token的log_probability之和 / 回答长度的token数
python
data_dict = {
'image': image,
"question": question,
"chosen": chosen,
"rejected": rejected,
"idx": sample['idx'],
"metainfo": metainfo
}
logps=json.loads(sample['logps']) # 调用/muffin下面的./eval/muffin_inference_logp.py
if type(logps) == type([]):
(data_dict['ref_win_logp'], data_dict['ref_win_avg_logp'], data_dict['ref_win_per_token_logp'],
data_dict['ref_rej_logp'], data_dict['ref_rej_avg_logp'], data_dict['ref_rej_per_token_logp']) = logps
else:
(data_dict['ref_win_logp'], data_dict['ref_win_avg_logp'], data_dict['ref_win_per_token_logp'],
data_dict['ref_rej_logp'], data_dict['ref_rej_avg_logp'], data_dict['ref_rej_per_token_logp']) = logps['logps']
return data_dict2.2 计算log prob
python
def get_batch_logps(logits: torch.FloatTensor, labels: torch.LongTensor, return_per_token_logp=False, return_all=False, tokenizer=None) -> torch.FloatTensor:
"""Compute the log probabilities of the given labels under the given logits.
Args:
logits: Logits of the model (unnormalized). Shape: (batch_size, sequence_length, vocab_size)
labels: Labels for which to compute the log probabilities. Label tokens with a value of -100 are ignored. Shape: (batch_size, sequence_length)
Returns:
A tensor of shape (batch_size,) containing the average/sum log probabilities of the given labels under the given logits.
"""
assert logits.shape[:-1] == labels.shape, f'logits.shape[:-1]={logits.shape[:-1]}, labels.shape={labels.shape}'
labels = labels[:, 1:].clone()
logits = logits[:, :-1, :]
loss_mask = (labels != -100)
# dummy token; we'll ignore the losses on these tokens later
labels[labels == -100] = 0
per_token_logps = torch.gather(logits.log_softmax(-1), dim=2,
index=labels.unsqueeze(2)).squeeze(2) # get log probabilities for each token in labels
log_prob = (per_token_logps * loss_mask).sum(-1)
average_log_prob = log_prob / loss_mask.sum(-1)2.3 DPO loss
- policy model指的是正在训练的模型,ref model是之前SFT阶段的模型
- 注意policy_chosen_logps这些是log 的probability,所以和原始的DPO的loss公式是完全等价的
python
def get_beta_and_logps(data_dict, model, args, is_minicpm=False, is_llava15=False):
win_input_ids = data_dict.pop('win_input_ids')
rej_input_ids = data_dict.pop('rej_input_ids')
ref_win_logp = data_dict.pop('ref_win_logp')
ref_rej_logp = data_dict.pop('ref_rej_logp')
log_prob, average_log_prob = get_batch_logps(
output.logits, concatenated_labels, return_per_token_logp=False)
if args.dpo_use_average:
concatenated_logp = average_log_prob
win_size = win_input_ids.shape[0]
rej_size = rej_input_ids.shape[0]
policy_win_logp, policy_rej_logp = concatenated_logp.split(
[win_size, rej_size]) # 默认的是average的log_logits,值越大越置信
return policy_win_logp, policy_rej_logp, ref_win_logp, ref_rej_logp, beta
def dpo_loss(policy_chosen_logps: torch.FloatTensor,
policy_rejected_logps: torch.FloatTensor,
reference_chosen_logps: torch.FloatTensor,
reference_rejected_logps: torch.FloatTensor,
beta: float,
reference_free: bool = False) -> Tuple[torch.FloatTensor, torch.FloatTensor, torch.FloatTensor]:
"""Compute the DPO loss for a batch of policy and reference model log probabilities.
Args:
policy_chosen_logps: Log probabilities of the policy model for the chosen responses. Shape: (batch_size,)
policy_rejected_logps: Log probabilities of the policy model for the rejected responses. Shape: (batch_size,)
reference_chosen_logps: Log probabilities of the reference model for the chosen responses. Shape: (batch_size,)
reference_rejected_logps: Log probabilities of the reference model for the rejected responses. Shape: (batch_size,)
beta: Temperature parameter for the DPO loss, typically something in the range of 0.1 to 0.5. We ignore the reference model as beta -> 0.
reference_free: If True, we ignore the _provided_ reference model and implicitly use a reference model that assigns equal probability to all responses.
Returns:
A tuple of three tensors: (losses, chosen_rewards, rejected_rewards).
The losses tensor contains the DPO loss for each example in the batch.
The chosen_rewards and rejected_rewards tensors contain the rewards for the chosen and rejected responses, respectively.
"""
pi_logratios = policy_chosen_logps - policy_rejected_logps # log(\pi(a_i | x)) - log(\pi(b_i | x)) = log(\pi(a_i | x) / \pi(b_i | x))
ref_logratios = reference_chosen_logps - reference_rejected_logps # 完全等价的
if reference_free:
ref_logratios = 0
logits = pi_logratios - ref_logratios
losses = -F.logsigmoid(beta * logits)
chosen_rewards = beta * (policy_chosen_logps -
reference_chosen_logps).detach()
rejected_rewards = beta * \
(policy_rejected_logps - reference_rejected_logps).detach()
return losses, chosen_rewards, rejected_rewards
############# 调用为
policy_win_logp, policy_rej_logp, ref_win_logp, ref_rej_logp, beta = get_beta_and_logps(
data_dict, model, self.args, is_llava15=True) # 这些都是averaged的token的log_logits
losses, chosen_rewards, rejected_rewards = dpo_loss(policy_win_logp,
policy_rej_logp,
ref_win_logp,
ref_rej_logp,
beta=beta)