《算法导论》第 1 章 - 算法在计算中的作用

大家好！今天我们开始一起学习经典的算法著作《算法导论》。作为开篇，第 1 章主要介绍算法的基本概念以及它在计算领域中的重要性。无论你是刚入门的编程爱好者，还是有一定经验的开发者，理解算法的基础概念都至关重要。让我们一起探索算法的世界吧！

1.1 算法

什么是算法？

算法 是定义良好的计算过程，它取一个或一组值作为输入，并产生一个或一组值作为输出。简单来说，算法就是一系列解决问题的清晰指令。

日常生活中也有很多 "算法" 的例子：

• 菜谱就是一种算法：输入是食材，输出是菜肴
• 导航路线就是一种算法：输入是起点和终点，输出是行驶路线

在计算机科学中，算法是解决计算问题的核心。例如：

• 排序算法：输入一组无序的数字，输出一组有序的数字
• 搜索算法：输入一个集合和一个目标值，输出目标值在集合中的位置

算法示例：排序问题

让我们通过两个经典的排序算法来理解算法的概念：插入排序 和归并排序。

插入排序

插入排序的基本思想是：将一个记录插入到已经排好序的有序表中，从而得到一个新的、记录数增 1 的有序表。

#include <iostream>
#include <vector>

using namespace std;

// 插入排序函数
// 输入：一个整数向量的引用
// 输出：无（直接对输入向量进行排序）
void insertionSort(vector<int>& arr) {
    // 获取数组长度
    int n = arr.size();
    
    // 从第二个元素开始遍历（第一个元素默认已排序）
    for (int i = 1; i < n; i++) {
        int key = arr[i];  // 当前要插入的元素
        int j = i - 1;     // 已排序部分的最后一个元素索引
        
        // 将大于key的元素向后移动一位
        while (j >= 0 && arr[j] > key) {
            arr[j + 1] = arr[j];
            j--;
        }
        // 将key插入到正确的位置
        arr[j + 1] = key;
    }
}

// 打印数组元素
void printArray(const vector<int>& arr) {
    // 使用迭代器代替范围for循环，兼容C++98
    for (vector<int>::const_iterator it = arr.begin(); it != arr.end(); ++it) {
        cout << *it << " ";
    }
    cout << endl;
}

int main() {
    // 测试插入排序
    // 使用C++98兼容的方式初始化vector
    vector<int> arr;
    arr.push_back(5);
    arr.push_back(2);
    arr.push_back(4);
    arr.push_back(6);
    arr.push_back(1);
    arr.push_back(3);
    
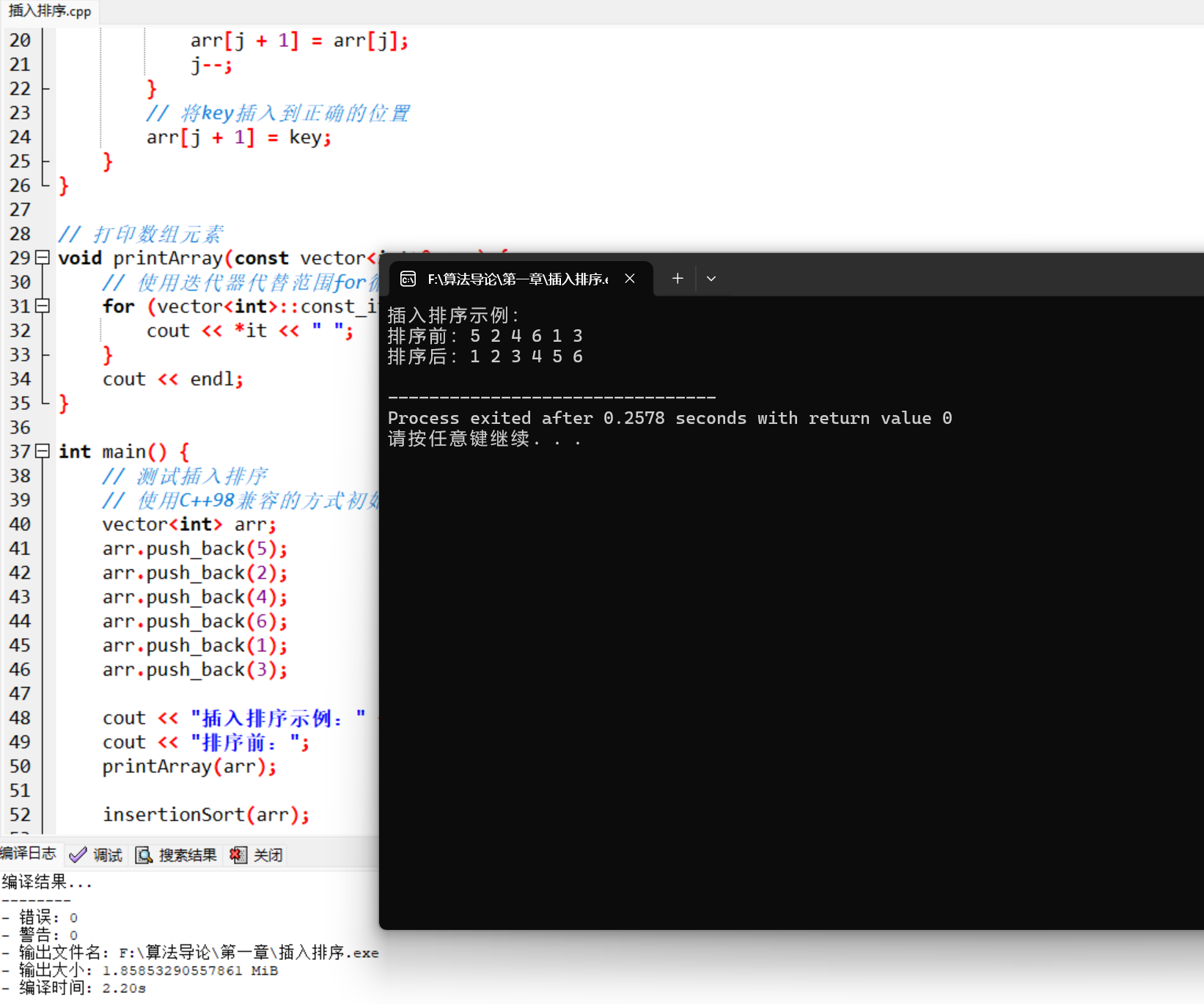
    cout << "插入排序示例：" << endl;
    cout << "排序前：";
    printArray(arr);
    
    insertionSort(arr);
    
    cout << "排序后：";
    printArray(arr);
    
    return 0;
}

归并排序

归并排序采用分治法策略，将问题分解为更小的子问题，解决子问题后再将结果合并。

#include <iostream>
#include <vector>
#include <algorithm> // 用于copy

using namespace std;

// 合并两个已排序的子数组
// arr: 原始数组
// left: 左子数组的起始索引
// mid: 左子数组的结束索引（右子数组的起始索引-1）
// right: 右子数组的结束索引
void merge(vector<int>& arr, int left, int mid, int right) {
    // 计算两个子数组的大小
    int n1 = mid - left + 1;
    int n2 = right - mid;
    
    // 创建临时数组
    vector<int> L(n1), R(n2);
    
    // 复制数据到临时数组
    copy(arr.begin() + left, arr.begin() + mid + 1, L.begin());
    copy(arr.begin() + mid + 1, arr.begin() + right + 1, R.begin());
    
    // 合并临时数组回原数组
    int i = 0;  // 左子数组的起始索引
    int j = 0;  // 右子数组的起始索引
    int k = left;  // 合并后数组的起始索引
    
    while (i < n1 && j < n2) {
        if (L[i] <= R[j]) {
            arr[k] = L[i];
            i++;
        } else {
            arr[k] = R[j];
            j++;
        }
        k++;
    }
    
    // 复制左子数组剩余元素
    while (i < n1) {
        arr[k] = L[i];
        i++;
        k++;
    }
    
    // 复制右子数组剩余元素
    while (j < n2) {
        arr[k] = R[j];
        j++;
        k++;
    }
}

// 归并排序主函数
// arr: 要排序的数组
// left: 排序的起始索引
// right: 排序的结束索引
void mergeSort(vector<int>& arr, int left, int right) {
    if (left < right) {
        // 计算中间点
        int mid = left + (right - left) / 2;
        
        // 递归排序左半部分
        mergeSort(arr, left, mid);
        // 递归排序右半部分
        mergeSort(arr, mid + 1, right);
        
        // 合并已排序的两部分
        merge(arr, left, mid, right);
    }
}

// 打印数组元素（兼容C++98）
void printArray(const vector<int>& arr) {
    // 使用迭代器代替范围for循环
    for (vector<int>::const_iterator it = arr.begin(); it != arr.end(); ++it) {
        cout << *it << " ";
    }
    cout << endl;
}

int main() {
    // 测试归并排序
    // 使用C++98兼容的方式初始化vector
    vector<int> arr;
    arr.push_back(5);
    arr.push_back(2);
    arr.push_back(4);
    arr.push_back(6);
    arr.push_back(1);
    arr.push_back(3);
    
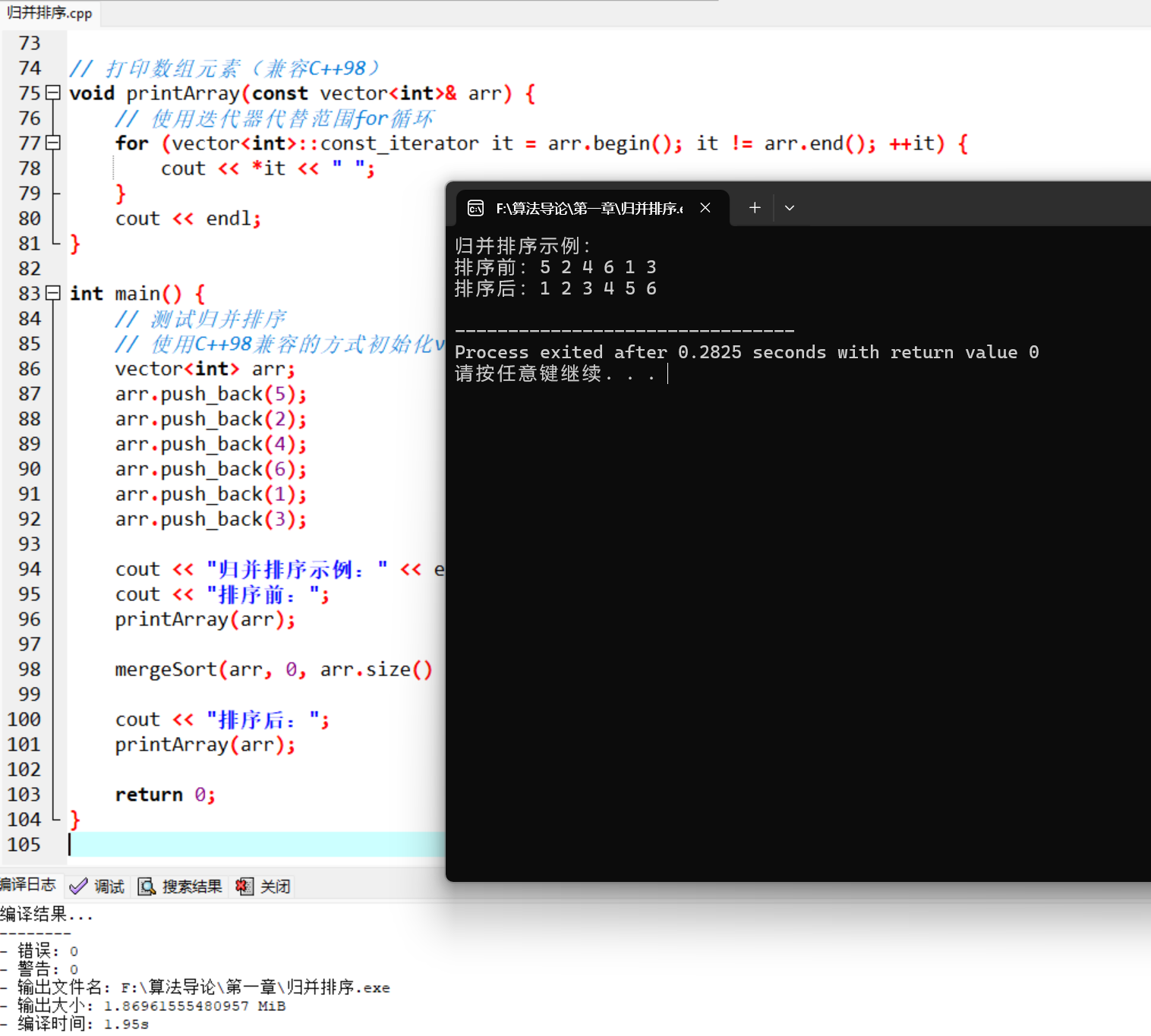
    cout << "归并排序示例：" << endl;
    cout << "排序前：";
    printArray(arr);
    
    mergeSort(arr, 0, arr.size() - 1);
    
    cout << "排序后：";
    printArray(arr);
    
    return 0;
}

算法的特性

一个好的算法应该具有以下特性：

• 正确性：能够正确地解决问题
• 效率 ：运行时间和空间消耗合理
• 确定性：每一步都有明确的定义
• 有限性：在有限步骤内结束
• 输入输出：有明确的输入和输出

1.2 作为一种技术的算法

算法不仅仅是解决问题的步骤，更是一种关键的技术。在计算机科学中，算法的效率直接影响系统的性能，甚至决定了一个问题能否在实际中被解决。

算法与其他技术的关系

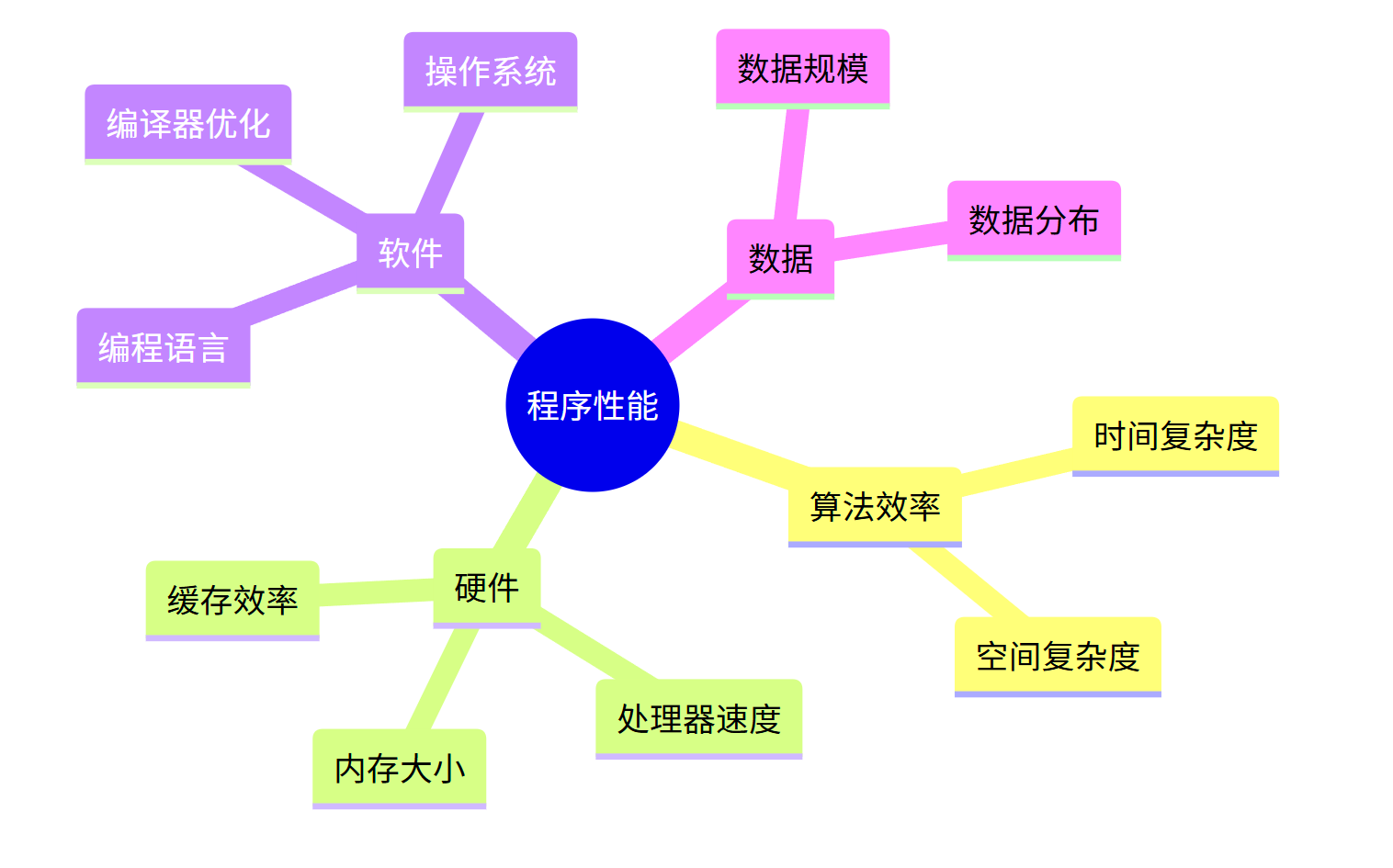
• 硬件：更快的硬件可以提升程序性能，但优秀的算法往往能带来更大的性能提升
• 编程语言：高效的编程语言可以优化执行效率，但无法弥补算法本身的低效
• 操作系统：优化的操作系统可以减少开销，但对计算密集型任务，算法仍起主导作用

算法复杂度的重要性

当处理大规模数据时，算法的效率变得尤为重要。例如：

• 对于 n 个元素的排序，插入排序的时间复杂度是 O (n²)
• 归并排序的时间复杂度是 O (n log n)

当 n 很大（如 100 万）时，O (n²) 算法可能需要数小时甚至数天，而 O (n log n) 算法可能只需要几秒。

综合案例：不同算法的性能对比

下面的代码比较了插入排序和归并排序在处理不同规模数据时的性能差异：

#include <iostream>
#include <vector>
#include <ctime>      // 用于C风格计时
#include <cstdlib>    // 用于C风格随机数
#include <algorithm>  // 用于copy

using namespace std;

// 插入排序
void insertionSort(vector<int>& arr) {
    int n = arr.size();
    for (int i = 1; i < n; i++) {
        int key = arr[i];
        int j = i - 1;
        while (j >= 0 && arr[j] > key) {
            arr[j + 1] = arr[j];
            j--;
        }
        arr[j + 1] = key;
    }
}

// 归并排序的合并函数
void merge(vector<int>& arr, int left, int mid, int right) {
    int n1 = mid - left + 1;
    int n2 = right - mid;
    
    vector<int> L(n1), R(n2);
    
    copy(arr.begin() + left, arr.begin() + mid + 1, L.begin());
    copy(arr.begin() + mid + 1, arr.begin() + right + 1, R.begin());
    
    int i = 0, j = 0, k = left;
    
    while (i < n1 && j < n2) {
        if (L[i] <= R[j]) {
            arr[k] = L[i++];
        } else {
            arr[k] = R[j++];
        }
        k++;
    }
    
    while (i < n1) arr[k++] = L[i++];
    while (j < n2) arr[k++] = R[j++];
}

// 归并排序主函数
void mergeSort(vector<int>& arr, int left, int right) {
    if (left < right) {
        int mid = left + (right - left) / 2;
        mergeSort(arr, left, mid);
        mergeSort(arr, mid + 1, right);
        merge(arr, left, mid, right);
    }
}

// 生成随机数组（C++98兼容版本）
vector<int> generateRandomArray(int size, int minVal, int maxVal) {
    vector<int> arr;
    // 初始化随机数种子
    srand(time(0));
    
    // 生成随机数并添加到数组
    for (int i = 0; i < size; i++) {
        // 生成[minVal, maxVal]范围内的随机数
        int num = minVal + rand() % (maxVal - minVal + 1);
        arr.push_back(num);
    }
    
    return arr;
}

// 测试排序算法性能
void testSortingPerformance(int arraySize) {
    // 生成随机数组
    vector<int> arr1 = generateRandomArray(arraySize, 1, 100000);
    vector<int> arr2 = arr1;  // 复制数组用于公平比较
    
    cout << "测试数组大小: " << arraySize << endl;
    
    // 测试插入排序
    clock_t start = clock();  // 记录开始时间
    insertionSort(arr1);
    clock_t end = clock();    // 记录结束时间
    double insertionTime = double(end - start) / CLOCKS_PER_SEC;  // 计算耗时（秒）
    cout << "插入排序时间: " << insertionTime << " 秒" << endl;
    
    // 测试归并排序
    start = clock();
    mergeSort(arr2, 0, arr2.size() - 1);
    end = clock();
    double mergeTime = double(end - start) / CLOCKS_PER_SEC;
    cout << "归并排序时间: " << mergeTime << " 秒" << endl;
    
    // 验证两种排序结果是否一致
    bool sortedCorrectly = true;
    for (int i = 0; i < arraySize; i++) {
        if (arr1[i] != arr2[i]) {
            sortedCorrectly = false;
            break;
        }
    }
    
    if (sortedCorrectly) {
        cout << "排序结果验证: 正确" << endl;
    } else {
        cout << "排序结果验证: 错误" << endl;
    }
    
    cout << "----------------------------------------" << endl;
}

int main() {
    cout << "算法性能对比测试" << endl;
    cout << "----------------------------------------" << endl;
    
    // 测试不同大小的数组
    testSortingPerformance(1000);    // 小数据集
    testSortingPerformance(10000);   // 中等数据集
    testSortingPerformance(100000);  // 大数据集
    
    // 对于非常大的数据集，插入排序会很慢，这里仅用归并排序演示
    vector<int> largeArr = generateRandomArray(1000000, 1, 100000);
    cout << "测试超大数组 (仅归并排序): " << largeArr.size() << endl;
    clock_t start = clock();
    mergeSort(largeArr, 0, largeArr.size() - 1);
    clock_t end = clock();
    double largeMergeTime = double(end - start) / CLOCKS_PER_SEC;
    cout << "归并排序时间: " << largeMergeTime << " 秒" << endl;
    
    return 0;
}

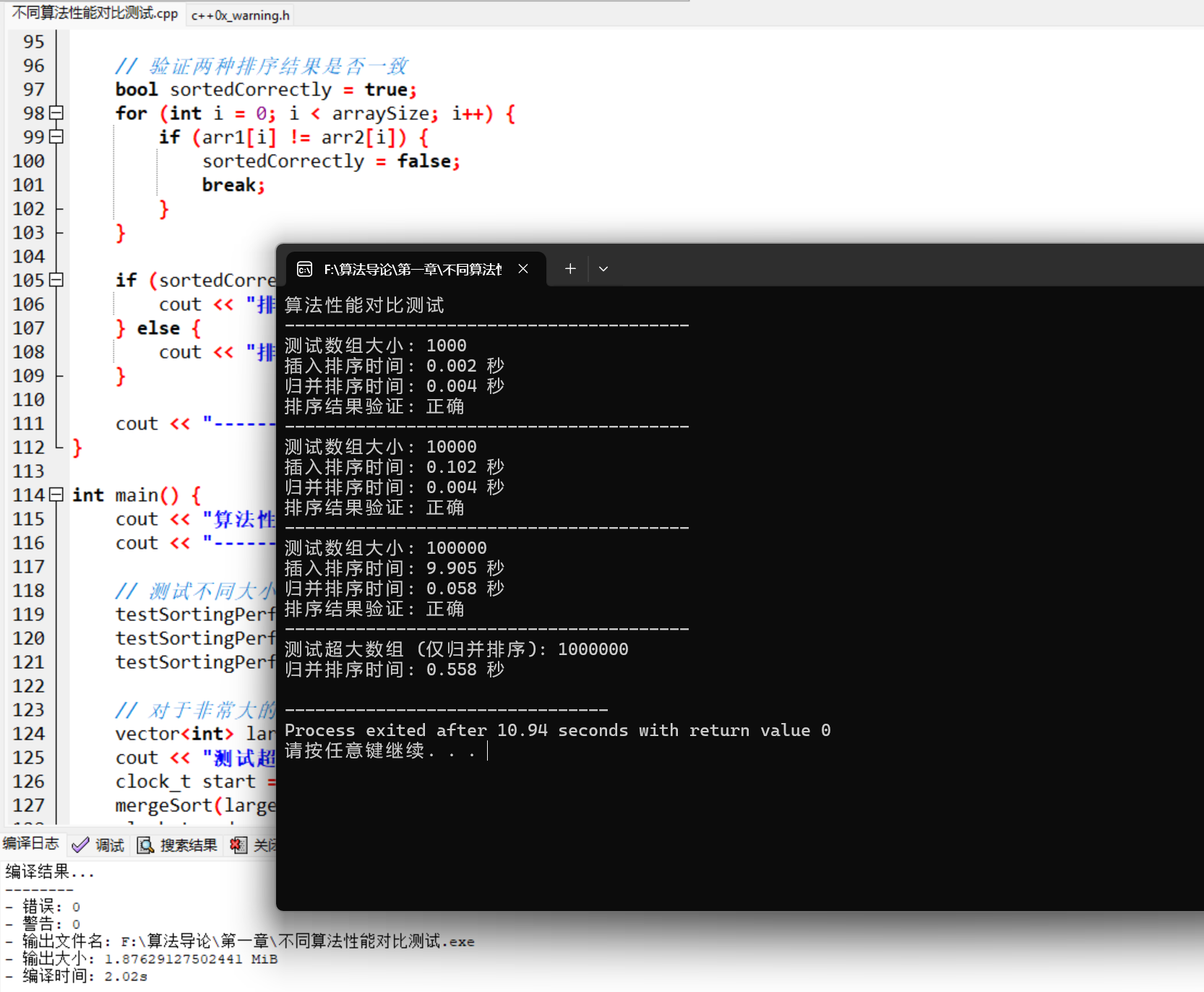
运行上述代码，你会发现：

• 对于小规模数据，两种算法的性能差异不大
• 随着数据规模增大，归并排序的优势越来越明显
• 对于非常大的数据集（如 100 万元素），插入排序可能需要过长时间，而归并排序仍能在合理时间内完成

影响程序性能的因素

思考题

1. 除了排序问题，请举出 3 个日常生活或编程中可以用算法解决的问题。

2. 比较插入排序和归并排序：

   哪种算法在最好情况下（输入已排序）性能更好？哪种算法对内存的要求更高？为什么？

3. 假设你需要编写一个程序来处理 10 亿个整数的排序，你会选择哪种算法？为什么？

4. 尝试实现一个简单的搜索算法，在一个整数数组中查找特定值并返回其位置。如果找不到，返回 - 1。

5. 思考：为什么说算法是一种技术？它与其他计算机技术（如硬件、编程语言）有何异同？

本章注记

• 《算法导论》（Introduction to Algorithms）由 Thomas H. Cormen、Charles E. Leiserson、Ronald L. Rivest 和 Clifford Stein 合著，通常被简称为 "CLRS"。
• 算法分析的历史可以追溯到 20 世纪 30 年代，由图灵、丘奇等数学家奠定基础。
• 现代计算机科学中，算法的重要性日益凸显，特别是在人工智能、大数据处理等领域。
• 学习算法不仅能提高程序效率，更能培养解决问题的逻辑思维能力。

结语

本章介绍了算法的基本概念和其作为一种技术的重要性。通过插入排序和归并排序的例子，我们看到了不同算法在解决同一问题时的效率差异。

在后续章节中，我们将深入学习各种算法设计技巧、分析方法以及具体的经典算法。掌握这些知识，将为你成为一名优秀的程序员或计算机科学家打下坚实基础。

如果你对本章内容有任何疑问或建议，欢迎在评论区留言讨论！让我们一起在算法的世界中探索前行！