【论文阅读】Transformer Feed-Forward Layers Are Key-Value Memories

Transformer Feed-Forward Layers Are Key-Value Memories

• 原文摘要

  • 研究背景与问题：

    • 前馈层占Transformer模型参数总量的2/3，但其功能机制尚未得到充分研究

  • 核心发现 ：提出++前馈层实质上是键值存储系统++

    • 键：这里的键与训练数据中出现的特定**文本模式 **相关联。
      • 例如，一个键可能被"The capital of France is"这样的短语激活。
    • 值： 与每个键对应，这个值的++功能++ 是引导模型生成一个关于输出词汇的概率分布 。
      • 继续上面的例子，与"The capital of France is"这个键关联的值，会生成一个概率分布，其中 "Paris" 这个词的概率会非常高。

  • 实验发现：

    • 学习到的文本模式具有人类可解释性

    • 层级分化现象：

      • 底层网络捕捉表层模式（如语法结构）

      • 高层网络学习语义模式（深层含义）

      • 键值协同机制：

      • 值分布会集中在可能跟随键模式出现的词汇上

      • 这种特性在高层网络中尤为显著

  • 模型工作机制：

    • 组合输出 : 单个前馈层的输出并不是只激活了一个记忆，而是其内部 多个键值记忆的组合。

    • 逐层精炼 : 这个组合后的输出，会通过残差连接传递到模型的下一层。

      • 在后续的网络层中，这个输出会被 不断地修正和精炼。

    • 最终结果: 经过所有层的处理和精炼，模型最终生成了用于预测下一个词的概率分布。

1. 介绍

• 研究背景：

  • 现状描述：基于Transformer的语言模型（如BERT、GPT）已成为NLP领域的主流架构

  • 研究失衡：

    • 自注意力机制获得大量研究关注
    • 实际参数分布：自注意力层仅占1/3参数（4d²），前馈层占主要参数（8d²）

  • 核心问题：前馈层在Transformer中的具体功能机制是什么？

• 理论突破

  • 核心观点：前馈层在功能上模拟了神经记忆

    • 结构对应关系：
      • 第一参数矩阵 → 记忆键（keys）
      • 第二参数矩阵 → 记忆值（values）

    • 机制：

      

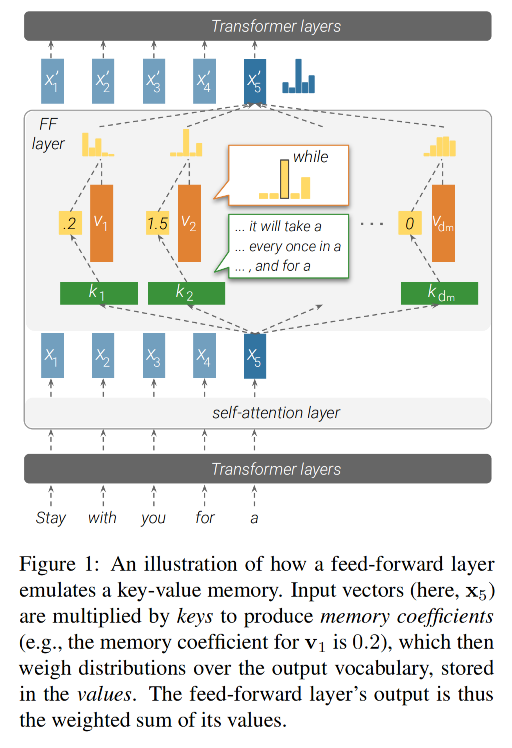
      • 键 与模型的输入进行交互，生成一组系数。
      • 然后，这些系数被用来对值 进行加权求和，从而得到该层的输出。
  • 创新点：首次系统分析前馈层存储的具体记忆内容

• 实证发现

  • 键特性 :
    • 每个键都与一组特定的、人类可以理解的输入模式 相关。
    • 这些模式可以是 n-gram (如固定词组)，也可以是 语义主题。
  • 值特性 :
    • 每个值都能导出一个关于输出词汇的概率分布。
    • 这个分布与它对应的键后面最可能出现的下一个词高度相关，这种相关性在模型的高层尤其明显。

• 系统工作机制：

  • 记忆组合机制：

    • 每层整合数百个活跃记忆单元
    • 产生与单个记忆值性质不同的复合分布

  • 残差连接功能：

    • 精炼机制：逐层微调预测分布
    • 信息保留：保持底层信息的持续传递

• 核心结论:

  • 前馈层在所有层级中都充当了输入模式的检测器。

  • 模型的最终输出分布，是一个通过所有层 自下而上地、逐步构建 起来的结果。

2. 前馈层作为未归一化的键值记忆结构

2.1 Feed-forward 层

• 前馈层特性

  • 在 Transformer 中，前馈层是逐位置处理的

  • 每一个 token 的向量都单独通过 FFN，不考虑别的位置。

  • 输入向量记为： x ∈ R d x \in \mathbb{R}^d x∈Rd（d 是隐藏维度）

• 数学表达式
  F F ( x ) = f ( x ⋅ K ⊤ ) ⋅ V FF(x) = f(x \cdot K^\top) \cdot V FF(x)=f(x⋅K⊤)⋅V

  • K ∈ R d m × d K \in \mathbb{R}^{d_m \times d} K∈Rdm×d：key 参数矩阵

  • V ∈ R d m × d V \in \mathbb{R}^{d_m \times d} V∈Rdm×d：value 参数矩阵

  • f ( ⋅ ) f(\cdot) f(⋅) ：非线性函数（如 ReLU）

  • m m m 是隐藏维度数量，表示++记忆单元个数++

2.2 神经记忆

• 神经记忆组成

  • 神经记忆由一组 key-value 对组成（也称 memory cells）

    • 神经记忆论文中就是用Memory去乘以对应的嵌入矩阵

    • 每个 k i k_i ki 是一个 d 维向量，构成整个 key 矩阵 K ∈ R d m × d K \in \mathbb{R}^{d_m \times d} K∈Rdm×d

    • 每个 v i v_i vi 是一个 d 维向量，构成 value 矩阵 V ∈ R d m × d V \in \mathbb{R}^{d_m \times d} V∈Rdm×d

• 神经记忆的输出形式 ：
  p ( k i ∣ x ) ∝ e x p ( x ⋅ k i ) → 基于点积做 softmax 得到匹配概率 M N ( x ) = ∑ i = 1 d m p ( k i ∣ x ) ⋅ v i → 输出是记忆值的加权平均 p(k_i | x) ∝ exp(x · k_i) \rightarrow \text{基于点积做 softmax 得到匹配概率} \\ MN(x) = \sum^{d_m}_{i=1} p(k_i | x) · v_i \rightarrow \text{输出是记忆值的加权平均} p(ki∣x)∝exp(x⋅ki)→基于点积做 softmax 得到匹配概率MN(x)=i=1∑dmp(ki∣x)⋅vi→输出是记忆值的加权平均

  • 简化式
    M N ( x ) = s o f t m a x ( x ⋅ K ⊤ ) ⋅ V MN(x) = softmax(x \cdot K^\top) \cdot V MN(x)=softmax(x⋅K⊤)⋅V

• 神经记忆论文原文

2.3 FFN就是模拟神经记忆

• 两者的结构几乎完全一致，区别只在于：

  结构	前馈层 FFN	神经记忆 Memory
  输入与 key 的相似度计算	x ⋅ K ⊤ x \cdot K^\top x⋅K⊤	x ⋅ K ⊤ x \cdot K^\top x⋅K⊤
  激活函数	ReLU（非归一化）	softmax（归一化）
  输出	f(x \\cdot K\^\\top) \\cdot V	softmax(x \\cdot K\^\\top) \\cdot V

  • 区别 ：FFN 用的是 ReLU，没有归一化；神经记忆用的是 softmax，输出是概率分布。

• FFN 的隐藏层：记忆系数

  m = f ( x ⋅ K ⊤ ) m = f(x \cdot K^\top) m=f(x⋅K⊤)，这个激活向量其实就是每个 memory 的记忆系数

  • m ∈ R m m \in \mathbb{R}^m m∈Rm 是 FFN 中间的隐藏表示

  • 每个 m i m_i mi 就代表第 i i i 个记忆单元对当前输入的响应强度

    • 如果输入 x x x 很符合第 i i i 个 key ( k i k_i ki)，那么 m i m_i mi 就会很大

• 论文观点：

  • 每个 key 向量 k i k_i ki 会对输入序列中的某种模式（n-gram、短语、语义片段）产生响应
  • 对应的 value 向量 v i v_i vi 表示该模式之后的可能输出分布

3. 键捕捉输入模式

• 核心观点 ：
  • 在Transformer模型的前馈层 中，**键矩阵 K K K **的作用是检测输入序列中的特定模式。
  • 具体来说，每个矩阵中的每个向量 k i k_i ki对应输入前缀 x 1 , . . . , x j x_1,...,x_j x1,...,xj中的某种特定模式。

3.1 实验验证

• 实验目标 ：证明这些 Key 确实与某些++人类可解释的输入模式++存在强关联。

• 实验设置：

  • 模型 ：Baevski & Auli 的16层Transformer语言模型（基于WikiText-103训练）。
    • 每层前馈层的隐藏维度d=1024，dm=4096，总关键向量数量为dm·16=65,536。
  • 采样：从每层随机抽取10个关键向量（共160个）进行分析。
  • 数据：使用WikiText-103训练集的所有句子前缀计算记忆系数。

• 实验步骤

  1. 计算记忆激活值

     • 给定某个键 k i k_i ki，计算其在训练集（WikiText-103）中所有句子前缀上的记忆激活值 ：
       ReLU ( x j ℓ ⋅ k i ℓ ) \text{ReLU}(x_j^\ell \cdot k_i^\ell) ReLU(xjℓ⋅kiℓ)

       • 其中， x j ℓ x_j^\ell xjℓ 是前缀 x j x_j xj 在第 ℓ 层的表示， k i ℓ k_i^\ell kiℓ 是第 ℓ \ell ℓ 层的第 i i i 个关键向量。

     • 对每个句子，计算其所有前缀的记忆激活值。如：

       • 输入句子：I love dogs
       • 前缀：I、I love、I love dogs
       • 每个前缀都过模型第 ℓ \ell ℓ 层，得到向量 x j ℓ x_j^\ell xjℓ，然后与 key k i ℓ k_i^\ell kiℓ 做内积，ReLU 激活

  2. 选出激活值最大的 top-t 个例子

     • 选择与 k i ℓ k_i^\ell kiℓ 内积后激活值最高的前t个前缀（即触发示例）。

  3. 人工分析

     • 让人类专家（NLP研究生）对每个key k i k_i ki 的前25个触发示例进行标注，要求：

       • 识别至少出现在3个前缀中的重复模式------降低随机性
         • 例如某个 key 的 25 个高激活句子中有 5 个包含"in the middle of"，那这个短语可能就是该 key 的检测目标
       • 用自然语言描述这些模式；
       • 将模式分类为shallow或semantic
         • 浅层模式：如 n-gram、词形搭配
         • 语义模式：如主题、句子结构、语义场景

     • 每个前缀可能关联多个模式。

• 结果

  

3.2 结果

3.2.1 每个 memory 都与人类可识别的语言模式相关

• 专家标注结果 ：
  • 对于每一个key ，人类专家都能识别出至少1种模式 ，平均每个关键向量关联3.6种模式。
  • 65%-80% 的触发前缀（top触发示例）至少包含一种可识别的模式。
• 结论 ：
  • Key确实捕捉到了可解释的模式，而不仅仅是随机激活。
  • 这些模式在人类看来是明确的，表明前馈层的keys 在某种程度上类似于模式探测器。

3.2.2 浅层 key 更偏向于浅层模式

• Transformer 的底层 FFN 层（第1-9层）更擅长捕捉"表层语言结构"
• 而越往上的层，越倾向于捕捉语义一致性：
  • 虽然激活的句子在表面形式上不相似，但上下文语义很接近

3.2.3 通过局部修改验证模式敏感性

• 为了进一步验证浅层/深层关键向量的差异，作者进行了可控扰动实验：

  • 方法 ：
    • 对每个关键向量的top-50触发示例 进行三种修改 ：
      1. 删除第一个token（测试开头的影响）；
      2. 删除最后一个token（测试结尾的影响）；
      3. 随机删除一个token（作为基线）。
    • 然后测量这些修改对记忆系数的影响。

• 结果（图3）：

  • 模型更关注句子的尾部 （比如，删除最后一个词，对激活影响更大）
    • 说明模型的 FFN 更敏感于前缀的结尾部分
  • 但在深层 FFN 中，删除最后一个词影响反而小
    • 说明：深层 key 并不依赖于具体词序，而更多关注语义结构

4. 值表示词汇分布

• 核心目标 ：证明++每个 FFN 的 value 向量 v i v_i vi 可以近似看作是一个词汇分布，即预测下一个词的概率分布++。

4.1 方法：把 value 映射到词汇表上

p i = s o f t m a x ( v i ⋅ E ) p_i= softmax(v_i \cdot E) pi=softmax(vi⋅E)

• 解释

  • v i v_i vi：某个 FFN 中的 value 向量
  • E E E：模型的输出 embedding 矩阵（每一行表示一个词的嵌入向量）
  • p i p_i pi：是一个概率分布，表示：如果只靠这个 v i v_i vi来预测，会最倾向于哪个词？

• 说明

  • 由于实际的模型预测不仅用了 v i v_i vi，还用了激活系数，所以这个 p i p_i pi 是一种理想化的预测分布，不能代表真实概率，但可以用来分析。

  • 也就是说：我们可以看它最喜欢哪个词（即 argmax），但不能直接当成语言模型输出概率。

4.2 value 的 top 预测是否匹配 key 激活句子的下一个词？

• 探究：如果一个 key 检测到了某个输入模式，那么它对应的 value 是否预测了这句话接下来的下一个词？

• 验证方式：

  1. 对每个 key k i ℓ k_i^\ell kiℓ，找到激活它最强的句子（top-1 trigger example），记作 x 1 , . . . , x j x_1, ..., x_j x1,...,xj

  2. 这句话的下一个token记为 w i ℓ w_i^\ell wiℓ

  3. 比较这个token是否就是 value 对应分布 p i p_i pi 中得分最高的词

     • 即： a r g m a x ( p i ) = = w i ℓ argmax(p_i) == w_i^\ell argmax(pi)==wiℓ 是否成立

• 结果

  • 层数从 1 到 10：匹配率接近 0%

  • 从第 11 层开始：匹配率迅速上升，到达约 3.5%

  • 虽然这个数值不高，但论文指出：

    远高于随机猜词的匹配率（0.0004%）

    说明这是++非随机的语言现象++

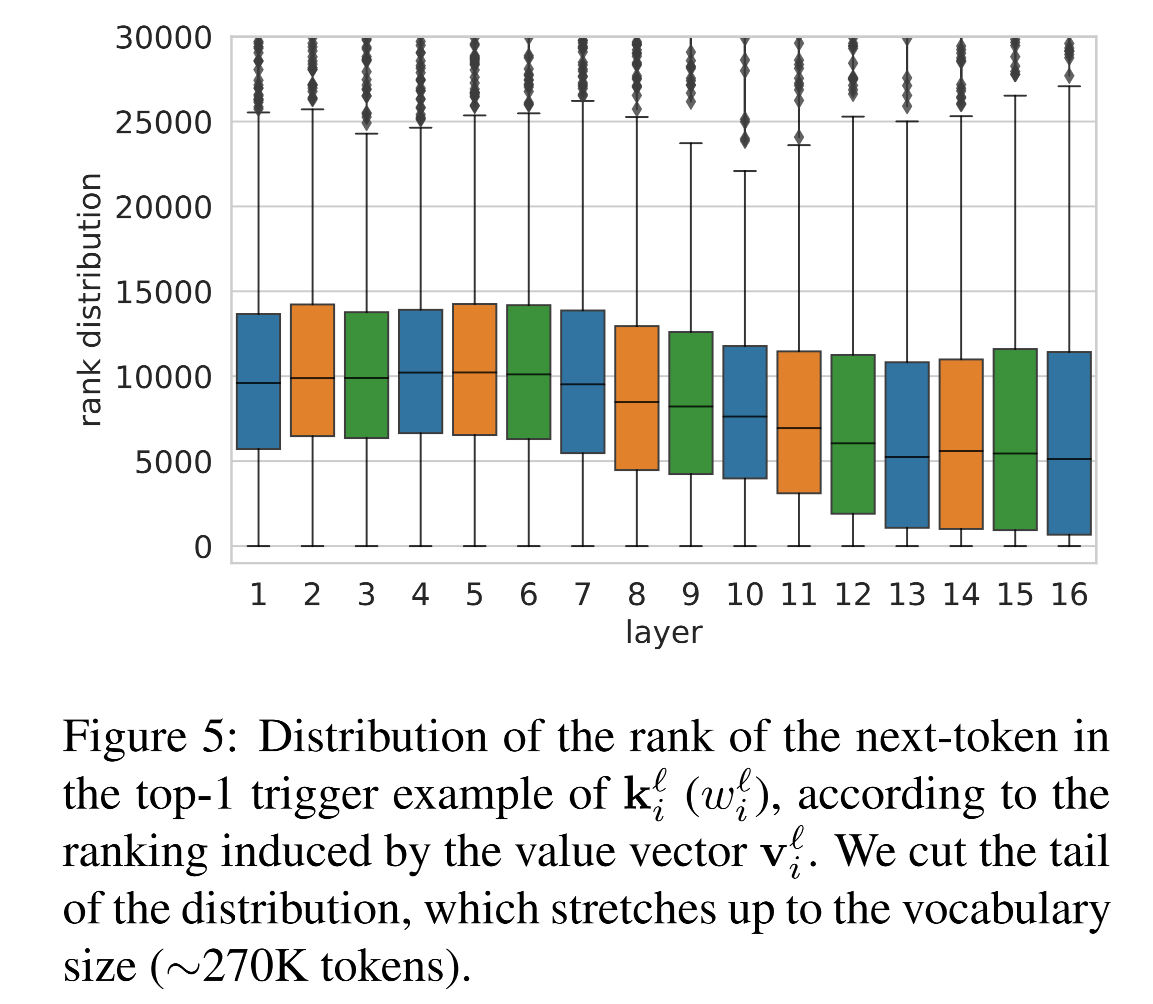
4.3 value 分布中预测词的排序越来越靠前

• 进一步探究：即使正确token不是top-1，那个正确的token在 value 预测分布中排第几？

  

  • 在上层，key 所对应句子的下一个token，在 value 的预测中，排序越来越靠前

  • 说明 value 越来越倾向于预测出 key 对应前缀之后的词

4.4 哪些value具有更强的预测性

• 探究：能否找出那些真正有预测能力的 value ？

• 方法：

  1. 观察每个 value 分布中 top-1 的概率值 （即 m a x ( p i ) max(p_i) max(pi)）

  2. 如果这个值很大，说明这个 value 特别偏向某一个token

  3. 检查这类 value 是否更可能匹配 key 的激活句子？

     • 即value预测的结果是否是key触发示例的下一个token

• 结果

  • 值向量的最大概率越高，其预测与关键向量模式的匹配率也越高。
  • 在所有层中，选取Top 100最高概率的值向量，发现：
    • 97个来自高层（11-16层），仅3个来自低层。
    • 46个值向量（46%） 的Top预测与至少一个关键向量触发示例的下一个token匹配。

4.5 讨论

• 高层值向量具有预测能力 ：
  • 高层的值向量 v i ℓ v_i^\ell viℓ倾向于预测关键向量 k i ℓ k_i^\ell kiℓ模式的下一个词token，表明它们存储了模式→预测的映射关系。
  • 例如，如果关键向量检测到模式 "The capital of France is" ，则对应值向量可能会高概率预测 "Paris"。
• 低层值向量无显著预测能力 ：
  • 低层的值向量与关键向量模式无关，可能因为：
    • 低层的值向量不在输出词嵌入空间，导致投影后的分布无意义。
    • 低层更关注局部语法，而非语义预测。
• 部分中间层可能共享高层空间 ：
  • 某些中间层（如10-11层）的值向量开始表现出预测能力，表明Transformer的表示空间可能逐渐对齐。

5. 累加记忆

• 本节探究的核心问题

  1. 在一个前馈层内部，多个激活的 memory cell 是如何组合起来输出一个向量的？

  2. 多个前馈层之间是如何通过残差连接将这些组合进一步细化、优化的？

5.1 单个前馈层中多个 memory 的组合行为

• 前馈层的输出：
  y ℓ = ∑ i ReLU ( x ℓ ⋅ k i ℓ ) ⋅ v i ℓ + b ℓ y^\ell = \sum_i \text{ReLU}(x^\ell \cdot k_i^\ell) · v_i^\ell + b^\ell yℓ=i∑ReLU(xℓ⋅kiℓ)⋅viℓ+bℓ

  • 每个 key 向量 k i ℓ k_i^\ell kiℓ 与输入 x ℓ x^\ell xℓ 点积，经过 ReLU 得到激活系数

  • 对应的 value v i ℓ v_i^\ell viℓ 被加权求和

  • 加上 bias，得到这一层 FFN 的输出 y ℓ y^\ell yℓ

    每一层的输出是很多子预测的组合结果。

• 探究问题

  • 这些 value 到底是如何组合成一个输出的？
    • 是某个单独的 memory 主导？
    • 还是多个记忆单元共同决定？

• 实验设计：

  • 从验证集中的随机采样 4,000 个前缀

  • 验证集用于模拟模型在推理时的行为（而不是记忆训练样本）

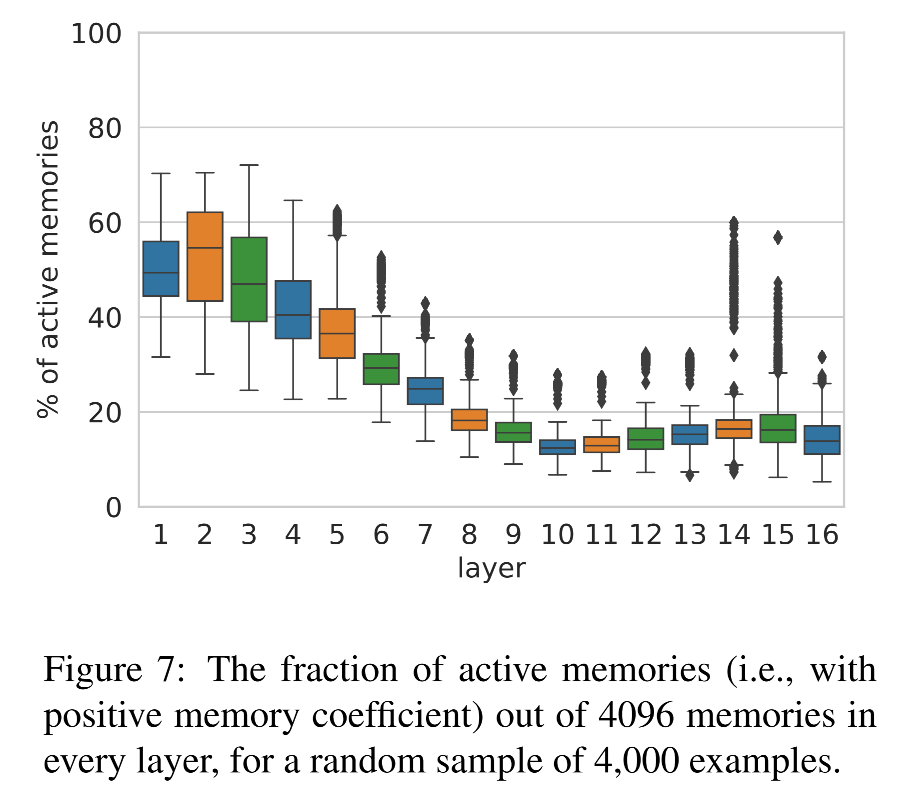
• 指标1：每层被激活的 memory 数量

  

  • 每一层中，大概有 10%--50%memory cell 被激活（也就是激活值 > 0）

  • 到了第 10 层，激活数量下降，正好对应之前在第3节提到++从浅层结构过渡到语义层++的临界点

• 指标2：输出是否由单一记忆主导的？

  • 定义 ： t o p ( h ) = a r g m a x ( h ⋅ E ) top(h) = argmax(h \cdot E) top(h)=argmax(h⋅E)

    • 即某个向量 h 的预测词是哪个（映射到词表）

  • 检验：当前层的输出向量 y ℓ y^\ell yℓ，是否等于某一个 value v i ℓ v_i^\ell viℓ 的预测结果？
    ∃ i : t o p ( v i ℓ ) = t o p ( y ℓ ) \exist i:top(v_i^\ell) = top(y^\ell) ∃i:top(viℓ)=top(yℓ)

    • 如果是，那就说明某个 memory 完全主导了预测。

  • 实验结果：在网络的任意层中，至少 68% 的预测和所有单个 memory 的预测都不一致。即：

    • 模型在大多数情况下，不会只依赖某个记忆单元来做预测

    • 而是将多个 memory 组合起来，产生了一个新分布

    • 这就是组合式预测

  • 补充分析：如果有单个memory的输出匹配，是为什么？

    • 在少数情况下，某个 memory cell 的预测正好是整层的预测，作者进一步分析这些例子：

      1. 60% 的预测是停用词（例如 "the", "of"）

      2. 43% 的输入前缀很短（少于 5 个词）

    • 观点：

      • 这些常见模式可能导致模型用某个 memory "缓存"了它们（类似缓存/记忆）

      • 因此对这些简单情况，不需要多个 memory 组合，单个 memory 就能给出准确预测

5.2 跨层预测改善

• 模型的前馈计算路径和残差机制
  x ℓ = L a y e r N o r m ( r ℓ ) y ℓ = F F ( x ℓ ) o ℓ = y ℓ + r ℓ x^\ell = LayerNorm(r^\ell)\\ y^\ell =FF(x^\ell)\\ o^\ell = y^\ell + r^\ell xℓ=LayerNorm(rℓ)yℓ=FF(xℓ)oℓ=yℓ+rℓ

  • r ℓ r^\ell rℓ：来自前一层的残差向量

  • 这些步骤说明：每一层并不会独立做决策，而是将上一层的"意见"作为基础，再进一步调整。

• 核心假设

  • 模型通过层层残差连接形成了一种逐层精化预测的机制
  • 早期层已经做出了部分决策，后续层只是慢慢地调整这些决策。

5.2.1 哪一层就已经决定了最终输出？

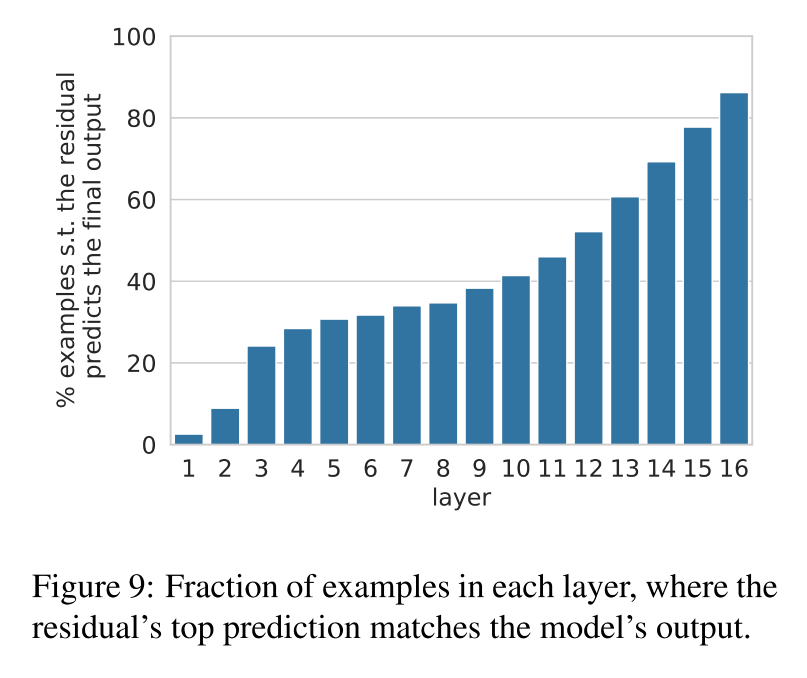
• 实验设计 ：对每一层 r ℓ r^\ell rℓ，检查它是否已经能预测出最终模型输出 o L o^L oL
  t o p ( r ℓ ) = t o p ( o L ) top(r^\ell) = top(o^L) top(rℓ)=top(oL)

• 结果：

  

  • 大约有三分之一的预测，早在底层（尤其是第10层之前）就已经确定了

  • 从第10层开始，这个比例迅速上升

• 说明：

  • 许多明确的预测在中层甚至底层就已经形成了

  • 上层更多在进行微调，而非决定性预测

5.2.2 每一层对最终预测的置信度是怎么变化的？

• 实验设计

  • 拿当前层的残差 r ℓ r^\ell rℓ

  • 对它做 softmax，得到词表分布 p p p

  • 查看它对最终预测词 w = t o p ( o L ) w = top(o^L) w=top(oL) 的概率是多少
    p = s o f t m a x ( r ℓ ⋅ E ) p w = p [ w ] p = softmax(r^\ell · E) \\ p_w = p[w] p=softmax(rℓ⋅E)pw=p[w]

• 结果：残差对最终预测的信心是逐层增强的

  

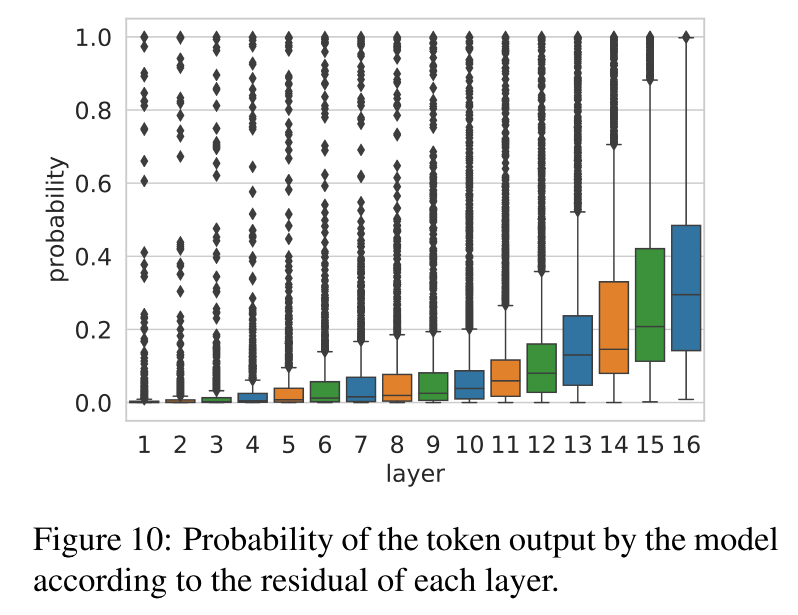
  • 模型逐层在收敛意见，越来越肯定这个预测是对的。

5.2.3 前馈层到底对残差做了什么事？

• 实验设计：检查三种情况，是哪个导致了输出的变化

  • t o p ( r ℓ ) top(r^\ell) top(rℓ)：残差原本的预测

  • t o p ( y ℓ ) top(y^\ell) top(yℓ)：前馈网络本层的预测

  • t o p ( o ℓ ) top(o^\ell) top(oℓ)：这两者相加之后的最终输出

• 三种交互类型：

  类型	条件	意义
  residual + agreement	t o p ( o ℓ ) = t o p ( r ℓ ) top(o^\ell) = top(r^\ell) top(oℓ)=top(rℓ)	前馈网络只是支持了残差的判断，没有改变它
  ffn override	KaTeX parse error: Undefined control sequence: \and at position 27: ... = top(y^\ell) \̲a̲n̲d̲ ̲top(o^\ell) \ne...	前馈层强势改变了残差的预测
  composition	t o p ( o ℓ ) ≠ t o p ( y ℓ ) ≠ t o p ( r ℓ ) top(o^\ell) \neq top(y^\ell) \neq top(r^\ell) top(oℓ)=top(yℓ)=top(rℓ)	输出是残差和前馈的折中

• 结果：

  

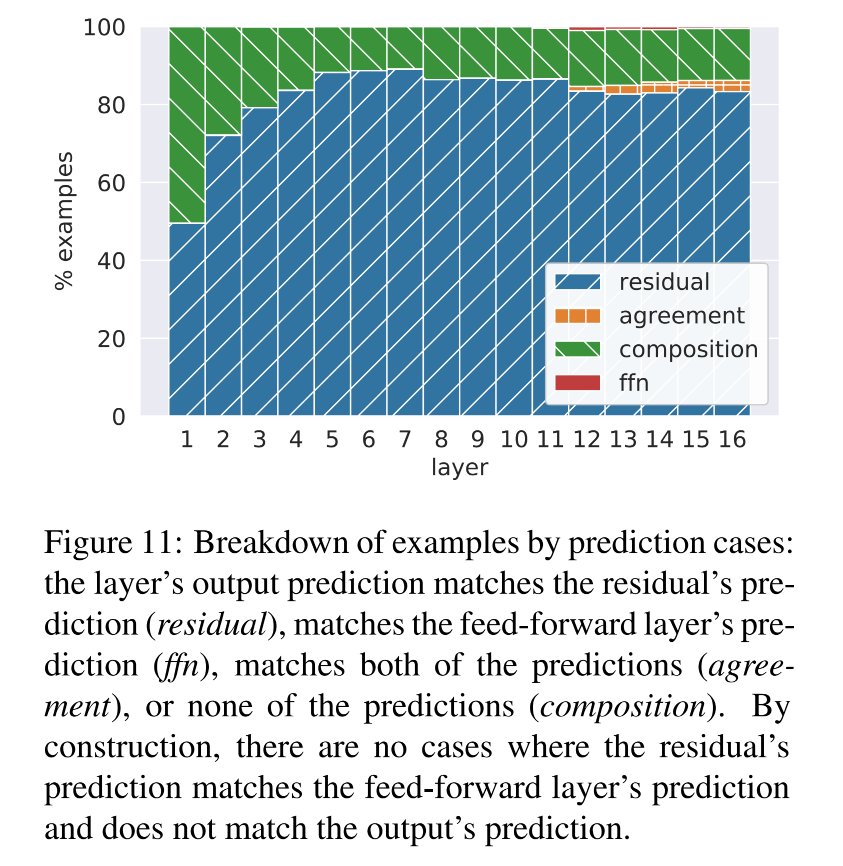
  • 绝大多数时候，最终输出等于残差预测（residual+agreement）

  • 只有极少数情况下是前馈预测主导（ffn override）

  • 有一定比例是二者的组合（composition）

• 结论：FFN 并不是直接替代残差预测，而是作为一种权重再分布机制，对残差输出进行修正或微调。

  • 现象：当前层的最终预测往往既不是残差向量的预测结果，也不是前馈层的预测结果，而是介于两者之间的折中预测
    • 猜测：前馈层有时会对 residual 中 top1 的token投否决票，从而把注意力引向其他候选词。

5.2.4 最后一层的改动是否有意义的？

• 人工看了 100 个最后一层中 FFN 改变残差预测的例子，发现：

  1. 66 个案例是语义上较远的跳变：

     • 例如："people" → "same"

  2. 34 个案例是语义相近的微调：

     • 例如："later" → "earlier"、"gastric" → "stomach"

• 即使在最后一层，前馈层仍然可以细调预测，表现出对语义的精细掌控能力。

6. 相关工作

• 神经元功能分析

  • 研究者通过分析单个神经元或神经元群体的激活情况，理解它们捕捉了哪些语言现象

  • 这些工作与模型架构无关，关注的是"神经元是否编码了语法、语义、世界知识等"。

• 卷积模型中的模式提取

  • Jacovi 分析了 CNN 在文本分类任务中，发现其能自动提取关键的 n-gram 模式。

  • 与本论文类似，也是寻找网络中自动学习到的可解释模式。

• Transformer 中的自注意力研究

  • 大量研究聚焦在 Transformer 的 self-attention 层的功能和可解释性

  • 也有一些研究探索 不同层级之间的功能差异

• 前馈层的研究仍然稀缺

  • 有少量论文提到 FFN可能具有独立重要性：
  • 但 它们都没有系统性地刻画 FFN 的机制，因此本论文填补了这一空白。