【数据结构与算法】刷题篇——环形链表的约瑟夫问题

文章目录

环形链表的约瑟夫问题：经典算法的实现与分析
- 问题背景
- 核心思路：环形链表解法
- - 算法特点
- 完整代码实现
- 代码执行流程解析
- - [1. 环形链表创建](#1. 环形链表创建)
  - [2. 约瑟夫求解过程](#2. 约瑟夫求解过程)
  - [3. 内存管理](#3. 内存管理)
- 算法优化方向
- 历史案例验证
- 总结

环形链表的约瑟夫问题：经典算法的实现与分析

问题背景

约瑟夫问题（Josephus problem）是一个著名的理论问题，源于公元1世纪犹太历史学家弗拉维奥·约瑟夫斯的记载。故事描述如下：

在罗马人占领乔塔帕特后，39个犹太人与Josephus及他的朋友躲到一个洞中。39个犹太人决定宁愿死也不要被人抓到，于是决定了一个自杀方式：41个人排成一个圆圈，由第1个人开始报数，每报数到第3人该人就必须自杀，然后再由下一个重新报数，直到所有人都自杀身亡为止。然而Josephus和他的朋友并不想遵从，Josephus将朋友与自己安排在第16个与第31个位置，于是逃过了这场死亡游戏。

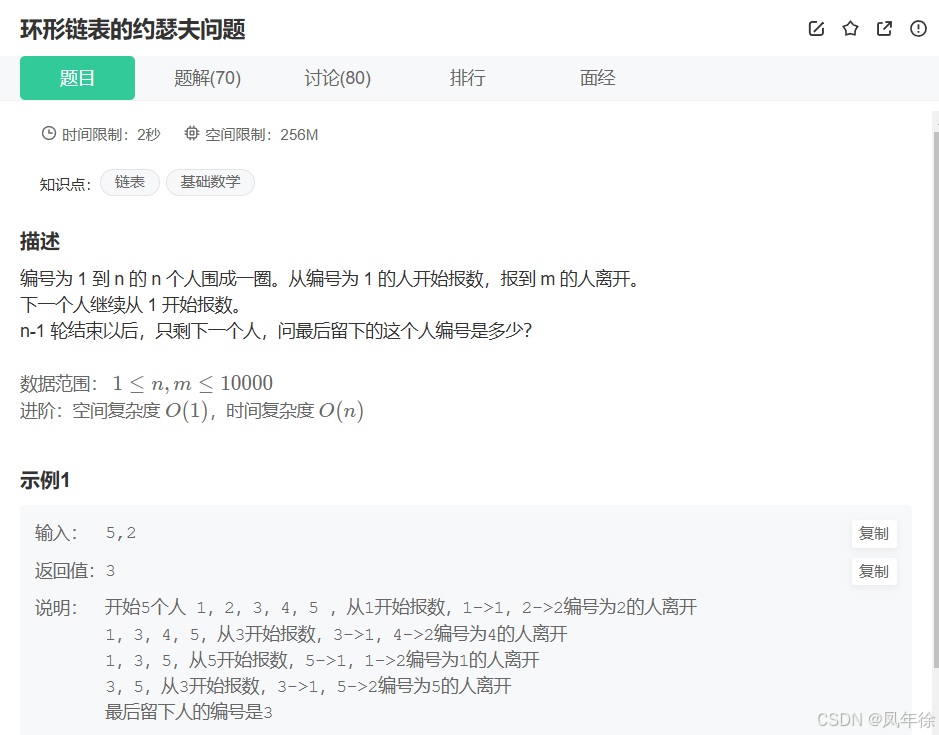
这个问题在计算机科学中被抽象为：

n个人围成一圈
从第一个人开始报数
每次数到m的人出局
从下一个人继续报数
求最后幸存者的编号

题目传送门

核心思路：环形链表解法

环形链表是解决约瑟夫问题的理想数据结构：

创建包含n个节点的环形链表
使用指针遍历链表，模拟报数过程
当计数达到m时，移除当前节点
重复上述过程，直到只剩一个节点
返回最后幸存节点的编号

算法特点

时间复杂度：O(n×m) - 最坏情况下需要遍历所有节点
空间复杂度：O(n) - 需要存储n个节点的链表
优点：直观模拟实际过程
缺点：当n很大时效率较低

完整代码实现

c 复制代码

#include <stdio.h>
#include <stdlib.h>

// 链表节点结构定义
typedef struct ListNode ListNode;
struct ListNode {
    int val;
    ListNode* next;
};

// 创建新节点
ListNode* buyNode(int i) {
    ListNode* newNode = (ListNode*)malloc(sizeof(ListNode));
    newNode->val = i;
    newNode->next = NULL;
    return newNode;
}

// 创建环形链表
ListNode* createCircularLinkedList(int n) {
    if (n <= 0) return NULL;
    
    ListNode* newHead = buyNode(1);  // 创建头节点
    ListNode* newTail = newHead;     // 尾指针初始指向头节点
    
    // 依次添加节点并形成环形
    for (int i = 2; i <= n; i++) {
        newTail->next = buyNode(i);  // 创建新节点并链接
        newTail = newTail->next;     // 移动尾指针
    }
    newTail->next = newHead;         // 首尾相连形成环
    return newTail;                  // 返回尾节点（方便后续操作）
}

// 约瑟夫环求解函数
int ysf(int n, int m) {
    if (n <= 0 || m <= 0) return 0;  // 处理无效输入
    
    // 创建环形链表并初始化指针
    ListNode* prev = createCircularLinkedList(n);
    ListNode* pcur = prev->next;     // 当前指针指向第一个节点
    int count = 1;                   // 报数计数器
    
    // 循环直到只剩一个节点
    while (prev != pcur) {
        if (count == m) {
            // 移除当前节点
            ListNode* nextNode = pcur->next;  // 保存下一个节点
            prev->next = nextNode;            // 跳过当前节点
            free(pcur);                       // 释放当前节点
            pcur = nextNode;                  // 移动到下一个节点
            count = 1;                        // 重置计数器
        } else {
            // 继续报数
            count++;
            prev = pcur;                      // 前驱指针跟进
            pcur = pcur->next;                // 当前指针后移
        }
    }
    
    // 处理最后剩余节点
    int result = prev->val;   // 保存结果值
    free(prev);               // 释放最后一个节点
    return result;            // 返回幸存者编号
}

代码执行流程解析

1. 环形链表创建

c 复制代码

ListNode* createCircularLinkedList(int n) {
    // 创建节点1作为头节点
    ListNode* newHead = buyNode(1);
    ListNode* newTail = newHead;
    
    // 添加后续节点
    for (int i = 2; i <= n; i++) {
        newTail->next = buyNode(i);
        newTail = newTail->next;
    }
    
    // 形成环形结构
    newTail->next = newHead;
    return newTail;  // 返回尾节点
}

创建包含n个节点的单向环形链表
每个节点存储其编号（从1开始）
返回尾节点指针，便于后续操作

2. 约瑟夫求解过程

c 复制代码

while (prev != pcur) {
    if (count == m) {
        // 移除当前节点
        ListNode* nextNode = pcur->next;
        prev->next = nextNode;
        free(pcur);
        pcur = nextNode;
        count = 1;
    } else {
        // 继续报数
        count++;
        prev = pcur;
        pcur = pcur->next;
    }
}

prev：指向当前节点的前驱节点
pcur：当前报数的节点
count：当前报数值（1到m）
当count达到m时，移除pcur指向的节点
否则继续移动指针报数

3. 内存管理

c 复制代码

int result = prev->val;  // 保存结果值
free(prev);              // 释放最后一个节点
return result;

最后幸存者存储在prev指向的节点
返回节点值后释放内存，避免泄漏
在移除节点过程中释放被淘汰节点

算法优化方向

虽然环形链表解法直观易懂，但有以下优化空间：

数学公式法：使用递推公式直接计算结果

c 复制代码

int josephus(int n, int m) {
    int result = 0;
    for (int i = 2; i <= n; i++) {
        result = (result + m) % i;
    }
    return result + 1;
}

时间复杂度：O(n)
空间复杂度：O(1)

位运算优化：当m=2时的特殊优化
递归解法：利用递归关系求解

历史案例验证

根据历史记载，当n=41，m=3时：

c 复制代码

printf("Josephus位置: %d\n", ysf(41, 3));  // 输出31

验证结果与历史记载一致：Josephus将自己的位置安排在第31号得以幸存。

总结

约瑟夫问题展示了数据结构在解决经典算法问题中的应用：

环形链表直观模拟了人员围成圆圈的场景
指针操作实现了报数和淘汰过程的模拟
注意边界条件处理和内存管理
理解不同解法的时空复杂度差异