目录

1.摘要
针对复杂应用场景下无人机集群路径规划效率和轨迹平滑性不足的问题,本文构建了一个包含多重约束条件的平滑覆盖路径规划模型,并在仿真环境中引入多形态障碍物以增强模型的工程适用性。通过采用 G2 连续的 Said-Ball 曲线对飞行路径进行参数化建模,并设置多个关键节点作为曲线端点,实现了更加灵活且平滑的轨迹生成。论文提出了一种多策略融合改进粒子群算法 ACDMRPSO,其有效提升了种群多样性和全局寻优能力。
2.无人机群平滑覆盖模型
本文建立了基于六项代价函数的平滑路径规划模型,并引入 G2 连续的 Said-Ball 曲线设计圆形检测轨迹以保证路径平滑性。其中,路径长度代价由各路径段欧氏距离之和确定,用于衡量飞行的能耗与时间成本。
F 1 = ∑ i = 1 N U ∑ j = 1 N P − 1 ∥ P i j P i j + 1 → ∥ F_1=\sum_{i=1}^{NU}\sum_{j=1}^{NP-1}\left\|\overrightarrow{P_{ij}P_{ij+1}}\right\| F1=i=1∑NUj=1∑NP−1 PijPij+1
其中, P i , j P_{i,j} Pi,j表示第 i i i架无人机的第 j j j个路径点, N U N_U NU为无人机数量, N P N_P NP为路径点数。为刻画复杂环境,本文构建了五类障碍物模型,包括三种底面分别平行于xoy 、xoz和zoy平面的圆柱体,以及长方体和球体。威胁代价:
F 2 = ∑ k = 1 N T ∑ i = 1 N U ∑ j = 1 N P − 1 T k ( P i , j P i , j + 1 → ) F_2 = \sum_{k=1}^{N_T} \sum_{i=1}^{N_U} \sum_{j=1}^{N_P-1} T_k\!\left(\overrightarrow{P_{i,j}P_{i,j+1}}\right) F2=k=1∑NTi=1∑NUj=1∑NP−1Tk(Pi,jPi,j+1 )
高度代价:
F 3 = ∑ i = 1 N U ∑ j = 1 N P H i , j F_3=\sum_{i=1}^{NU}\sum_{j=1}^{NP}H_{i,j} F3=i=1∑NUj=1∑NPHi,j
本文采用 Said-Ball 曲线构建无人机集群平滑覆盖路径模型,通过引入 G2 连续性条件保证多段曲线在连接处的曲率连续性,避免尖锐拐点,使轨迹更符合物理运动规律。利用自然启发式算法对 SBC 的控制顶点及 G2 连续参数进行联合优化,实现圆形检测路径的整体平滑生成。
将优化得到的参数转换为控制顶点后,对每条曲线离散生成路径点以计算平滑代价 F 4 F_{4} F4。其中,最大曲率和最大挠率分别反映轨迹形状变化和空间偏离程度,其数值越小,飞行轨迹越自然,路径整体平滑性越高。
F 4 = ∑ i = 1 N U ( w 1 ⋅ max ∣ k i ( t ) ∣ + w 2 ⋅ max ∣ τ i ( t ) ∣ ) , t ∈ [ 0 , 1 ] F_4=\sum_{i=1}^{NU}(w_1\cdot\max|k_i(t)|+w_2\cdot\max|\tau_i(t)|),t\in[0,1] F4=i=1∑NU(w1⋅max∣ki(t)∣+w2⋅max∣τi(t)∣),t∈[0,1]
无人机间避碰成本 F 5 F_5 F5:
F 5 = ∑ i = 1 N U ∑ j = 1 , j ≠ i N U ∑ k = 1 N P − 1 S i , j , k F_5=\sum_{i=1}^{NU}\sum_{j=1,j\neq i}^{NU}\sum_{k=1}^{NP-1}S_{i,j,k} F5=i=1∑NUj=1,j=i∑NUk=1∑NP−1Si,j,k
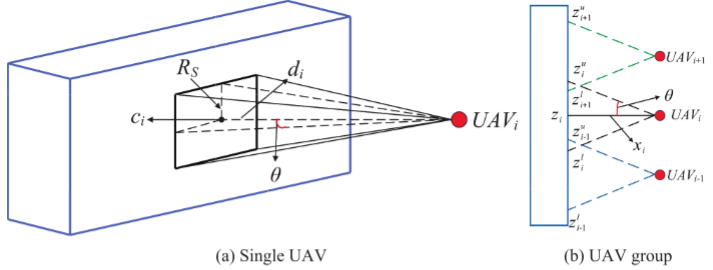
在检测任务中,无人机搭载水平相机形成固定尺寸的正方形视场,通过设定最大成像距离保证分辨率要求,并由几何关系确定覆盖角度。通过减少各无人机视场之间的重叠,提高集群对目标区域的整体覆盖效率。覆盖代价 F 6 F_{6} F6由协同覆盖高度和重叠高度共同决定:
F 6 = ϕ 1 ∑ j = 1 N P ( H w − C C H j ) + ϕ 2 ∑ j = 1 N P T O H j F_6=\phi_1\sum_{j=1}^{NP}\left(H_w-CCH_j\right)+\phi_2\sum_{j=1}^{NP}TOH_j F6=ϕ1j=1∑NP(Hw−CCHj)+ϕ2j=1∑NPTOHj
C C H j = ∑ i = 1 N U [ max ( 0 , min ( z i j μ , H w ) − max ( z i j l , z i − 1 , j μ ) ) ] CCH_j=\sum_{i=1}^{NU}\left[\max\left(0,\min(z_{ij}^\mu,H_w)-\max(z_{ij}^l,z_{i-1,j}^\mu)\right)\right] CCHj=i=1∑NU[max(0,min(zijμ,Hw)−max(zijl,zi−1,jμ))]
T O H j = ∑ i = 1 N U ∣ O P max ⋅ ( z i , j u − z i , j l ) − max ( z i , j l − z i − 1 , j u , 0 ) ∣ TOH_j=\sum_{i=1}^{NU}|OP_{\max}\cdot(z_{i,j}^u-z_{i,j}^l)-\max(z_{i,j}^l-z_{i-1,j}^u,0)| TOHj=i=1∑NU∣OPmax⋅(zi,ju−zi,jl)−max(zi,jl−zi−1,ju,0)∣
3.ACDMRPSO算法
其他常见策略,略~
变异进化种群动态策略
进化种群动力学(EPD)源于自组织临界性理论,通过淘汰适应度较差的个体以维持种群演化平衡。该机制在优良或劣质个体附近随机生成新个体,并用其替换原有劣质个体,从而加速种群向全局最优解收敛。改进EPD(MEPDS)针对劣质个体引入最优个体引导的更新策略,使其向最优解靠拢:
A X i t = C X i t + s i g n ( r 8 − 0.5 ) × ( U b − L b × R 6 + L b ) AX_i^t=CX_i^t+sign(r_8-0.5)\times(Ub-Lb\times R_6+Lb) AXit=CXit+sign(r8−0.5)×(Ub−Lb×R6+Lb)
C X i t = { X i t i = 1 , ⋯ , r o u n d ( 0.5 × N ) B P t i = r o u n d ( 0.5 × N ) + 1 , ⋯ , N \left.CX_i^t=\left\{\begin{array}{c}X_i^ti=1,\cdots,round(0.5\times N)\\BP^ti=round(0.5\times N)+1,\cdots,N\end{array}\right.\right. CXit={Xiti=1,⋯,round(0.5×N)BPti=round(0.5×N)+1,⋯,N
X i t + 1 = { D X i t i f f ( A X i t ) > f ( X i t ) A X i t e l s e \left.\boldsymbol{X}_i^{t+1}=\left\{\begin{array}{c}\boldsymbol{D}\boldsymbol{X}_i^t\mathrm{~if~f}(\boldsymbol{A}\boldsymbol{X}i^t)>\mathbf{f}(\boldsymbol{X}i^t)\\\boldsymbol{A}\boldsymbol{X}i^t\mathrm{~else}\end{array}\right.\right. Xit+1={DXit if f(AXit)>f(Xit)AXit else
D X i t = { X i t + J t × [ L b + R 7 × ( U b − L b ) ] × U 2 , if r 10 < A F , X i t + [ r 9 + A F × ( 1 − r 9 ) ] × ( X l 6 t − X l 7 t ) , else . DX_i^t = \begin{cases} X_i^t + J^t \times \bigl[\,Lb + R_7 \times (Ub - Lb)\,\bigr] \times U_2, & \text{if } r{10} < AF, \\[6pt] X_i^t + \bigl[r_9 + AF \times (1 - r_9)\bigr] \times \left( X{l_6}^t - X{l_7}^t \right), & \text{else}. \end{cases} DXit=⎩ ⎨ ⎧Xit+Jt×[Lb+R7×(Ub−Lb)]×U2,Xit+[r9+AF×(1−r9)]×(Xl6t−Xl7t),if r10<AF,else.
重启整数转换策略
重启整数转换策略通过能量因子实现探索与开发阶段的自适应切换:在探索阶段增强全局搜索能力,在开发阶段结合最优引导与 Levy 变异提高局部寻优精度。同时引入基于个体差异度的重启机制,对陷入局部最优的劣质个体进行随机重初始化,以恢复种群多样性并提升全局优化性能。

4.结果展示
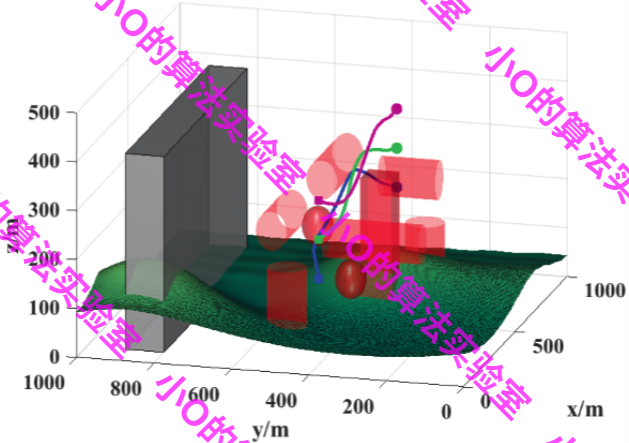

5.参考文献
1\] Hu G, Huang F, Houssein E H, et al. Smooth coverage path planning of unmanned aerial vehicles utilizing a novel multi-strategy integrated particle swarm optimization\[J\]. Advanced Engineering Informatics, 2026, 69: 104071. ### 6.代码获取 xx ### 7.算法辅导·应用定制·读者交流 xx