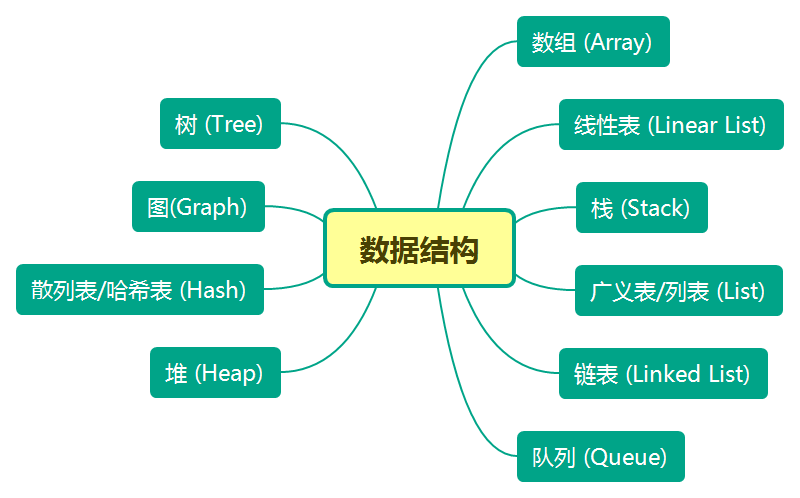
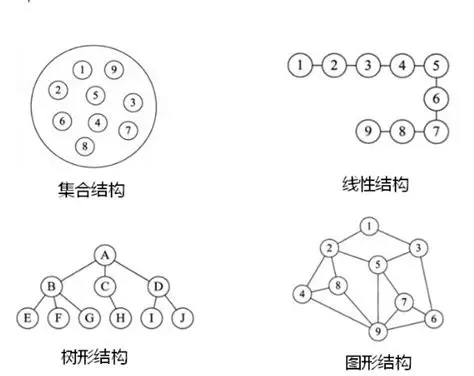
大家好!今天我们来深入学习《算法导论》第 10 章的内容 ------ 基本数据结构。这一章介绍了计算机科学中最基础也最常用的数据结构,包括栈、队列、链表、树等。这些结构是构建更复杂算法和系统的基石,掌握它们对于编程能力的提升至关重要。
本文不仅会讲解理论知识,还会提供完整可编译运行的 C++ 代码 ,每个知识点都配有综合应用案例,方便大家动手实践。话不多说,让我们开始吧!
思维导图
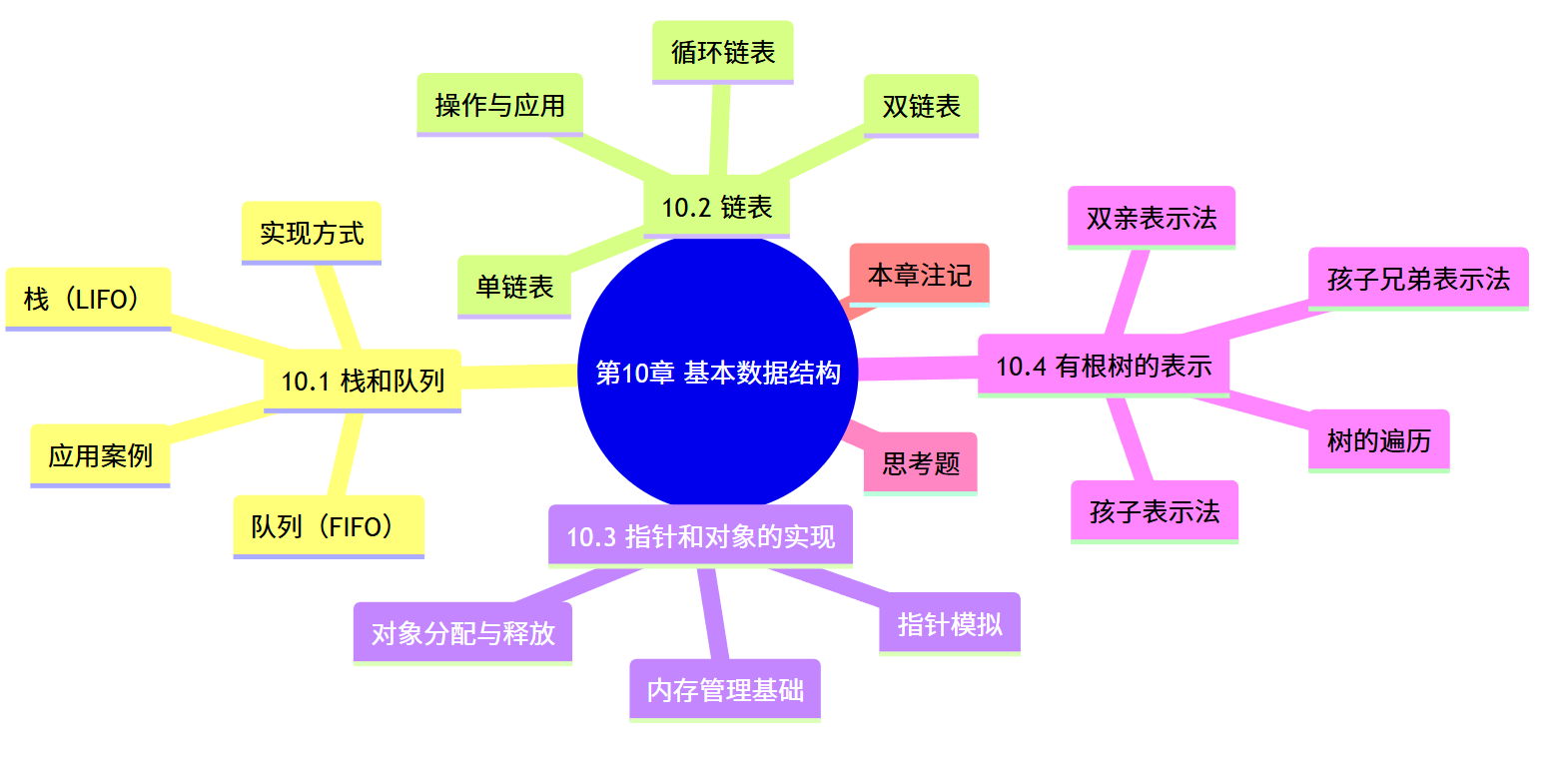
10.1 栈和队列
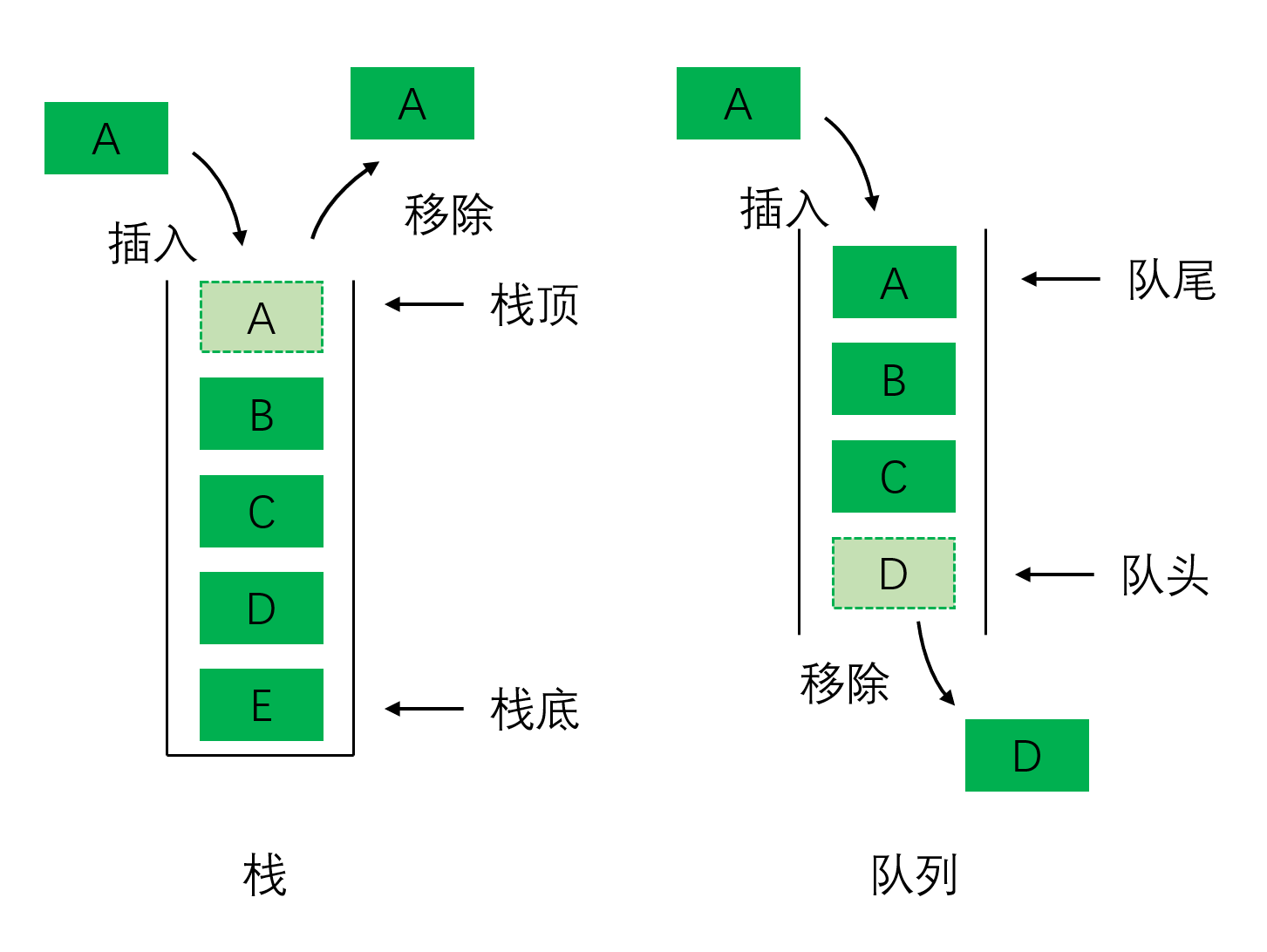
栈和队列是两种最基本的动态集合,它们的操作受到限制,是 "受限的线性表"。
10.1.1 栈(Stack)
栈是一种遵循后进先出(LIFO, Last In First Out) 原则的线性数据结构。想象一摞盘子,最后放上去的盘子总是最先被拿走,这就是栈的工作方式。
栈的基本操作:
push(S, x):将元素 x 压入栈 Spop(S):移除并返回栈 S 的栈顶元素top(S):返回栈 S 的栈顶元素(不删除)isEmpty(S):判断栈 S 是否为空
栈的实现(C++ 代码):
我们可以用数组或链表来实现栈,这里展示数组实现:
#include <iostream>
#include <stdexcept> // 用于异常处理
using namespace std;
const int MAX_SIZE = 100; // 栈的最大容量
class Stack {
private:
int data[MAX_SIZE]; // 存储栈元素的数组
int topIndex; // 栈顶指针(索引)
public:
// 构造函数:初始化空栈
Stack() : topIndex(-1) {}
// 判断栈是否为空
bool isEmpty() const {
return topIndex == -1;
}
// 判断栈是否已满
bool isFull() const {
return topIndex == MAX_SIZE - 1;
}
// 入栈操作
void push(int value) {
if (isFull()) {
throw runtime_error("栈已满,无法入栈");
}
data[++topIndex] = value; // 先移动指针,再存入元素
}
// 出栈操作
int pop() {
if (isEmpty()) {
throw runtime_error("栈为空,无法出栈");
}
return data[topIndex--]; // 先返回元素,再移动指针
}
// 获取栈顶元素
int top() const {
if (isEmpty()) {
throw runtime_error("栈为空,无法获取栈顶元素");
}
return data[topIndex];
}
// 获取栈的大小
int size() const {
return topIndex + 1;
}
// 打印栈中所有元素(从栈底到栈顶)
void print() const {
if (isEmpty()) {
cout << "栈为空" << endl;
return;
}
cout << "栈元素(栈底到栈顶):";
for (int i = 0; i <= topIndex; ++i) {
cout << data[i] << " ";
}
cout << endl;
}
};
// 测试栈的功能
int main() {
try {
Stack stack;
// 入栈操作
stack.push(10);
stack.push(20);
stack.push(30);
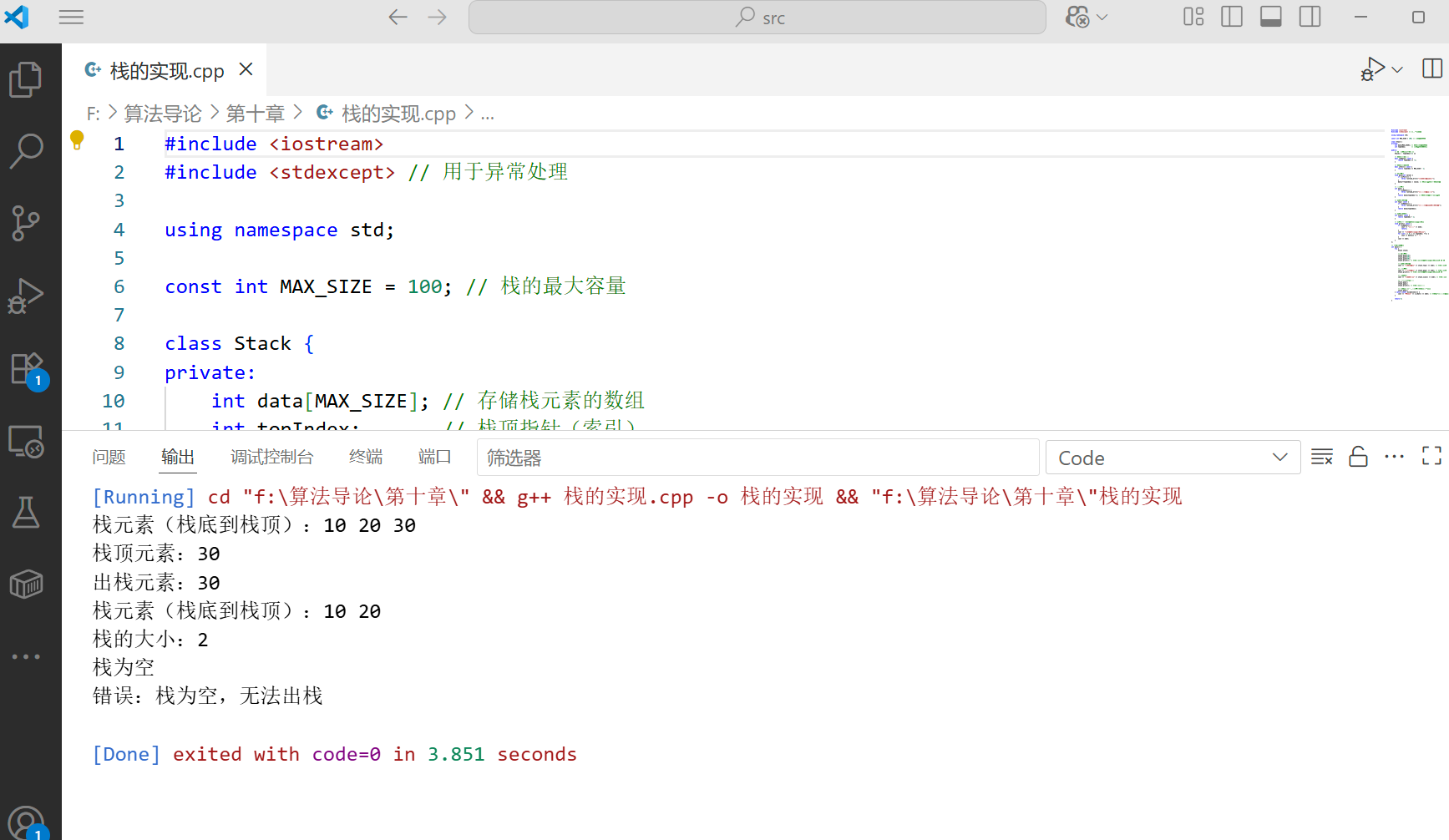
stack.print(); // 应输出:栈元素(栈底到栈顶):10 20 30
// 获取栈顶元素
cout << "栈顶元素:" << stack.top() << endl; // 应输出:30
// 出栈操作
cout << "出栈元素:" << stack.pop() << endl; // 应输出:30
stack.print(); // 应输出:栈元素(栈底到栈顶):10 20
// 栈的大小
cout << "栈的大小:" << stack.size() << endl; // 应输出:2
// 继续出栈直到为空
stack.pop();
stack.pop();
stack.print(); // 应输出:栈为空
// 尝试对空栈执行出栈操作(会抛出异常)
stack.pop();
} catch (const exception& e) {
cout << "错误:" << e.what() << endl; // 应捕获"栈为空,无法出栈"异常
}
return 0;
}栈操作流程图:
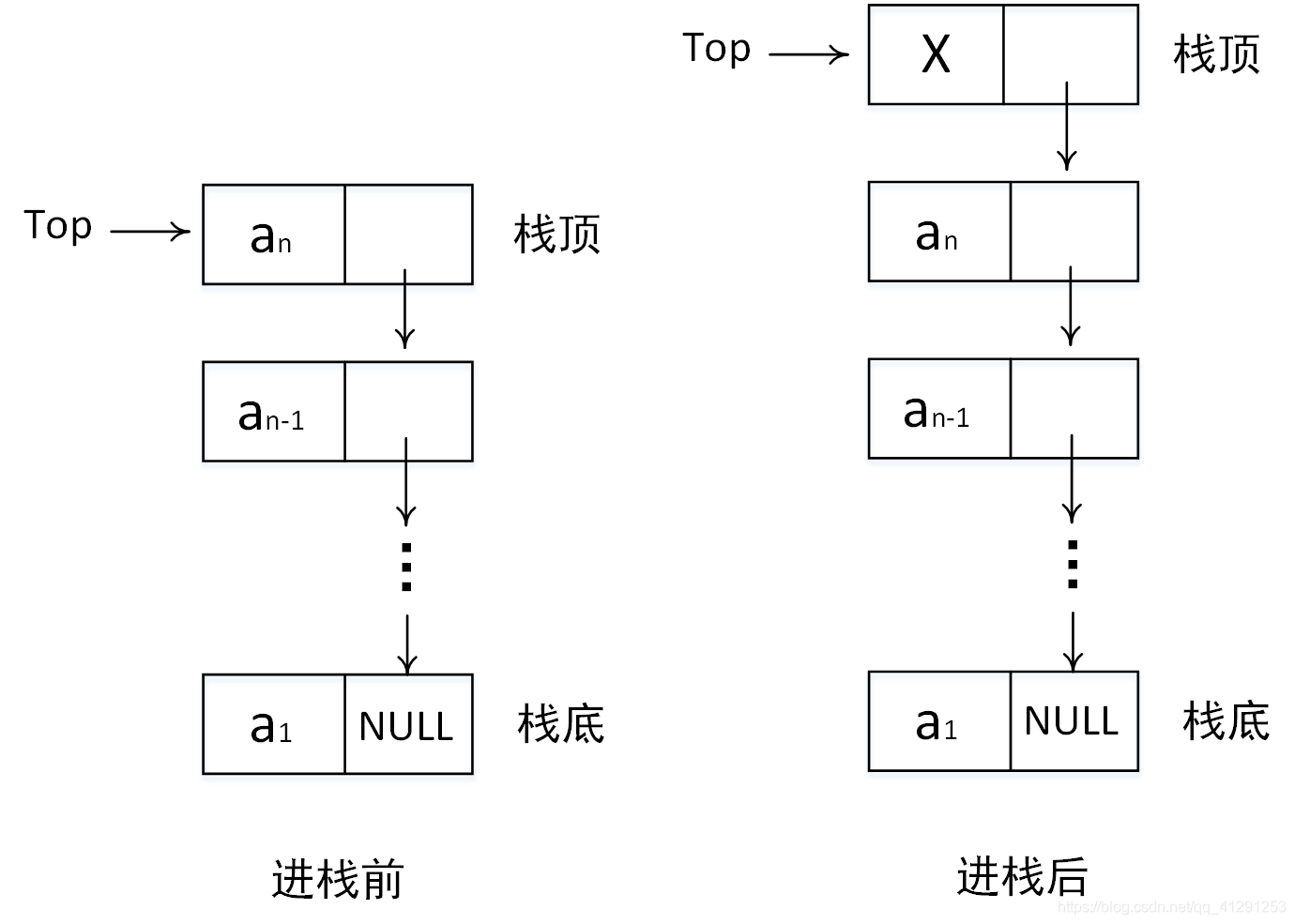
10.1.2 队列(Queue)
队列是一种遵循先进先出(FIFO, First In First Out) 原则的线性数据结构。就像排队买票,先到的人先买到票,这就是队列的工作方式。
队列的基本操作:
enqueue(Q, x):将元素 x 加入队列 Q 的队尾dequeue(Q):移除并返回队列 Q 的队头元素front(Q):返回队列 Q 的队头元素(不删除)isEmpty(Q):判断队列 Q 是否为空
队列的实现(C++ 代码):
队列可以用数组或链表实现,这里展示循环数组实现(解决普通数组实现的 "假溢出" 问题):
#include <iostream>
#include <stdexcept>
using namespace std;
const int MAX_SIZE = 100; // 队列的最大容量
class Queue {
private:
int data[MAX_SIZE]; // 存储队列元素的数组
int frontIndex; // 队头指针(索引)
int rearIndex; // 队尾指针(索引)
int count; // 队列中元素的数量
public:
// 构造函数:初始化空队列
Queue() : frontIndex(0), rearIndex(0), count(0) {}
// 判断队列是否为空
bool isEmpty() const {
return count == 0;
}
// 判断队列是否已满
bool isFull() const {
return count == MAX_SIZE;
}
// 入队操作:将元素添加到队尾
void enqueue(int value) {
if (isFull()) {
throw runtime_error("队列已满,无法入队");
}
data[rearIndex] = value; // 将元素存入队尾
rearIndex = (rearIndex + 1) % MAX_SIZE; // 循环移动队尾指针
count++; // 元素数量加1
}
// 出队操作:移除并返回队头元素
int dequeue() {
if (isEmpty()) {
throw runtime_error("队列为空,无法出队");
}
int frontValue = data[frontIndex]; // 保存队头元素
frontIndex = (frontIndex + 1) % MAX_SIZE; // 循环移动队头指针
count--; // 元素数量减1
return frontValue;
}
// 获取队头元素(不删除)
int front() const {
if (isEmpty()) {
throw runtime_error("队列为空,无法获取队头元素");
}
return data[frontIndex];
}
// 获取队列的大小
int size() const {
return count;
}
// 打印队列中所有元素(从队头到队尾)
void print() const {
if (isEmpty()) {
cout << "队列为空" << endl;
return;
}
cout << "队列元素(队头到队尾):";
int index = frontIndex;
for (int i = 0; i < count; ++i) {
cout << data[index] << " ";
index = (index + 1) % MAX_SIZE;
}
cout << endl;
}
};
// 测试队列的功能
int main() {
try {
Queue queue;
// 入队操作
queue.enqueue(10);
queue.enqueue(20);
queue.enqueue(30);
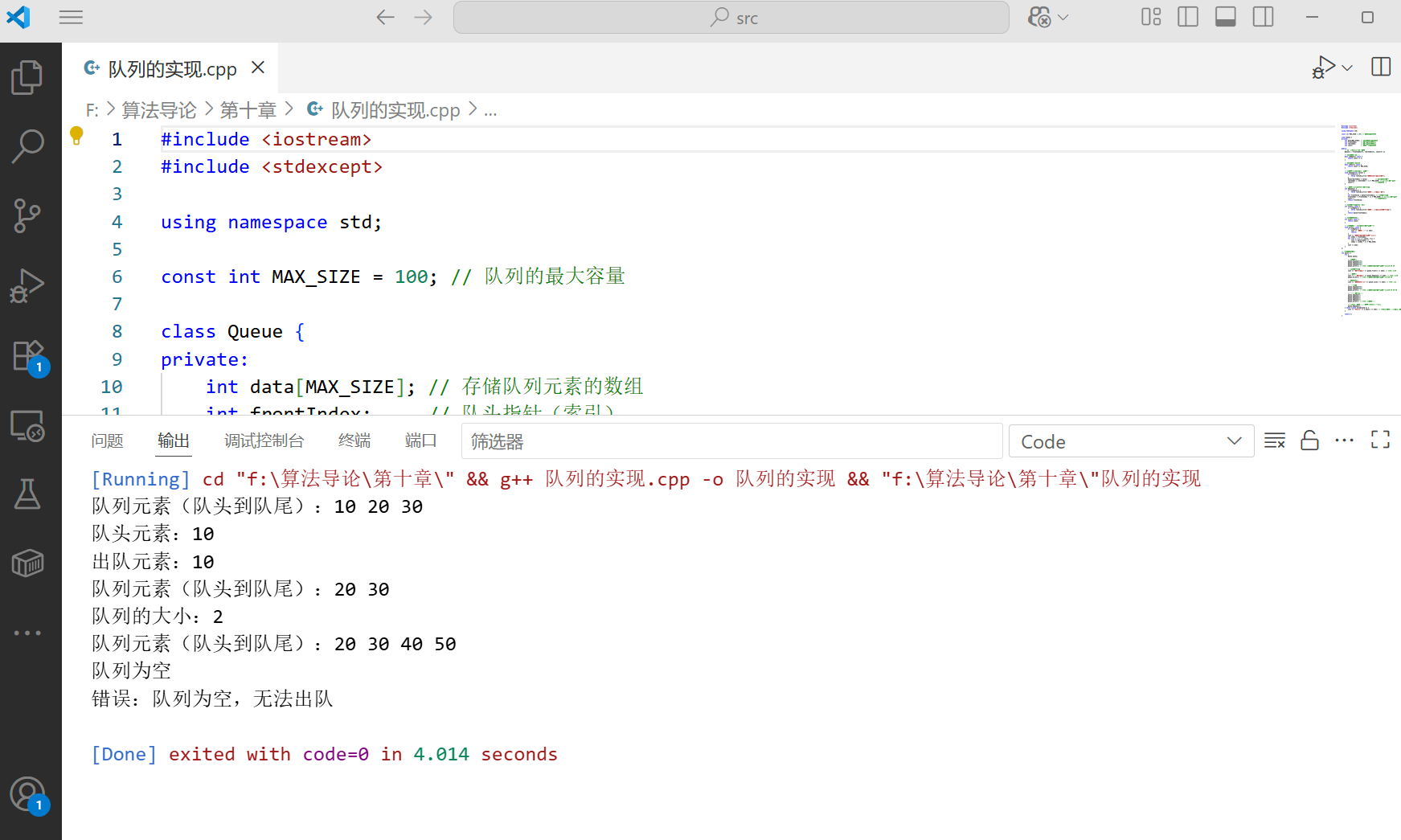
queue.print(); // 应输出:队列元素(队头到队尾):10 20 30
// 获取队头元素
cout << "队头元素:" << queue.front() << endl; // 应输出:10
// 出队操作
cout << "出队元素:" << queue.dequeue() << endl; // 应输出:10
queue.print(); // 应输出:队列元素(队头到队尾):20 30
// 队列的大小
cout << "队列的大小:" << queue.size() << endl; // 应输出:2
// 继续入队
queue.enqueue(40);
queue.enqueue(50);
queue.print(); // 应输出:队列元素(队头到队尾):20 30 40 50
// 继续出队直到为空
queue.dequeue();
queue.dequeue();
queue.dequeue();
queue.dequeue();
queue.print(); // 应输出:队列为空
// 尝试对空队列执行出队操作(会抛出异常)
queue.dequeue();
} catch (const exception& e) {
cout << "错误:" << e.what() << endl; // 应捕获"队列为空,无法出队"异常
}
return 0;
}队列操作流程图:
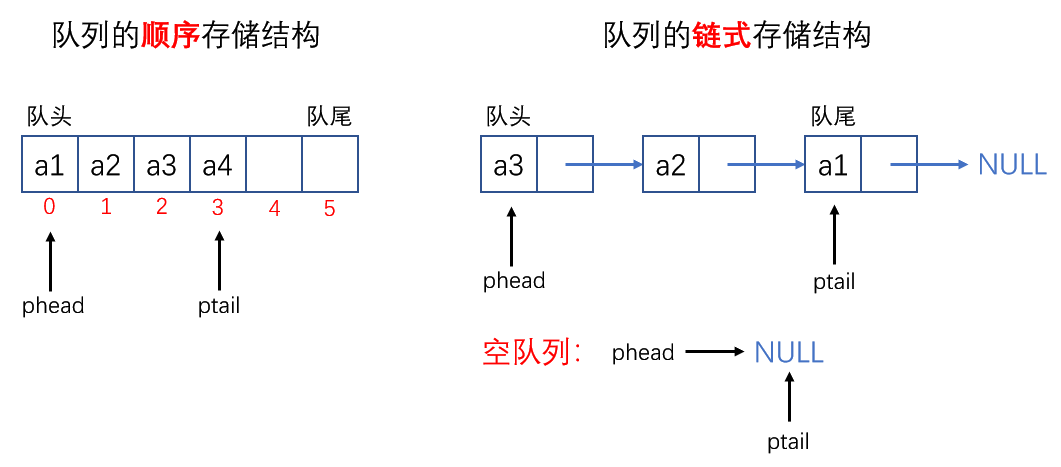
10.1.3 栈和队列的综合应用案例
案例 1:括号匹配问题(栈的应用)
括号匹配是栈的经典应用。给定一个包含括号()[]{} 的字符串,判断字符串中的括号是否匹配。
cpp
#include <iostream>
#include <string>
#include <stdexcept> // 用于异常处理
using namespace std;
// 栈的实现
const int MAX_SIZE = 100; // 栈的最大容量
class Stack {
private:
char data[MAX_SIZE]; // 存储栈元素的数组(改为char类型,因为要存储括号)
int topIndex; // 栈顶指针(索引)
public:
// 构造函数:初始化空栈
Stack() : topIndex(-1) {}
// 判断栈是否为空
bool isEmpty() const {
return topIndex == -1;
}
// 判断栈是否已满
bool isFull() const {
return topIndex == MAX_SIZE - 1;
}
// 入栈操作
void push(char value) {
if (isFull()) {
throw runtime_error("栈已满,无法入栈");
}
data[++topIndex] = value; // 先移动指针,再存入元素
}
// 出栈操作
char pop() {
if (isEmpty()) {
throw runtime_error("栈为空,无法出栈");
}
return data[topIndex--]; // 先返回元素,再移动指针
}
// 获取栈顶元素
char top() const {
if (isEmpty()) {
throw runtime_error("栈为空,无法获取栈顶元素");
}
return data[topIndex];
}
// 获取栈的大小
int size() const {
return topIndex + 1;
}
};
// 判断括号是否匹配
bool isBracketMatching(const string& s) {
Stack stack;
for (char c : s) {
// 如果是左括号,入栈
if (c == '(' || c == '[' || c == '{') {
stack.push(c);
}
// 如果是右括号
else if (c == ')' || c == ']' || c == '}') {
if (stack.isEmpty()) {
return false; // 右括号多了
}
char topChar = stack.pop();
// 检查是否匹配
if ((c == ')' && topChar != '(') ||
(c == ']' && topChar != '[') ||
(c == '}' && topChar != '{')) {
return false; // 括号类型不匹配
}
}
}
// 循环结束后栈应该为空,否则左括号多了
return stack.isEmpty();
}
int main() {
string test1 = "()[]{}";
string test2 = "([)]";
string test3 = "{[]}";
string test4 = "((()))";
string test5 = "(()";
cout << test1 << " 是否匹配:" << (isBracketMatching(test1) ? "是" : "否") << endl; // 是
cout << test2 << " 是否匹配:" << (isBracketMatching(test2) ? "是" : "否") << endl; // 否
cout << test3 << " 是否匹配:" << (isBracketMatching(test3) ? "是" : "否") << endl; // 是
cout << test4 << " 是否匹配:" << (isBracketMatching(test4) ? "是" : "否") << endl; // 是
cout << test5 << " 是否匹配:" << (isBracketMatching(test5) ? "是" : "否") << endl; // 否
return 0;
}案例 2:滑动窗口最大值(队列的应用)
给定一个整数数组和一个滑动窗口大小,找出所有滑动窗口里的最大值。
#include <iostream>
#include <vector>
#include <deque> // 双端队列,可高效地在两端进行插入和删除操作
using namespace std;
// 滑动窗口最大值
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
vector<int> result;
deque<int> q; // 存储索引,队列中对应的元素是单调递减的
for (int i = 0; i < nums.size(); ++i) {
// 移除队列中所有小于当前元素的元素,因为它们不可能成为最大值
while (!q.empty() && nums[i] >= nums[q.back()]) {
q.pop_back();
}
// 将当前元素的索引加入队列
q.push_back(i);
// 移除超出窗口范围的元素(窗口左边界为i - k + 1)
while (!q.empty() && q.front() <= i - k) {
q.pop_front();
}
// 当窗口大小达到k时,开始记录最大值(队列的 front 就是当前窗口的最大值)
if (i >= k - 1) {
result.push_back(nums[q.front()]);
}
}
return result;
}
// 打印向量
void printVector(const vector<int>& v) {
for (int num : v) {
cout << num << " ";
}
cout << endl;
}
int main() {
vector<int> nums1 = {1, 3, -1, -3, 5, 3, 6, 7};
int k1 = 3;
vector<int> result1 = maxSlidingWindow(nums1, k1);
cout << "滑动窗口最大值:";
printVector(result1); // 应输出:3 3 5 5 6 7
vector<int> nums2 = {1};
int k2 = 1;
vector<int> result2 = maxSlidingWindow(nums2, k2);
cout << "滑动窗口最大值:";
printVector(result2); // 应输出:1
return 0;
}10.2 链表
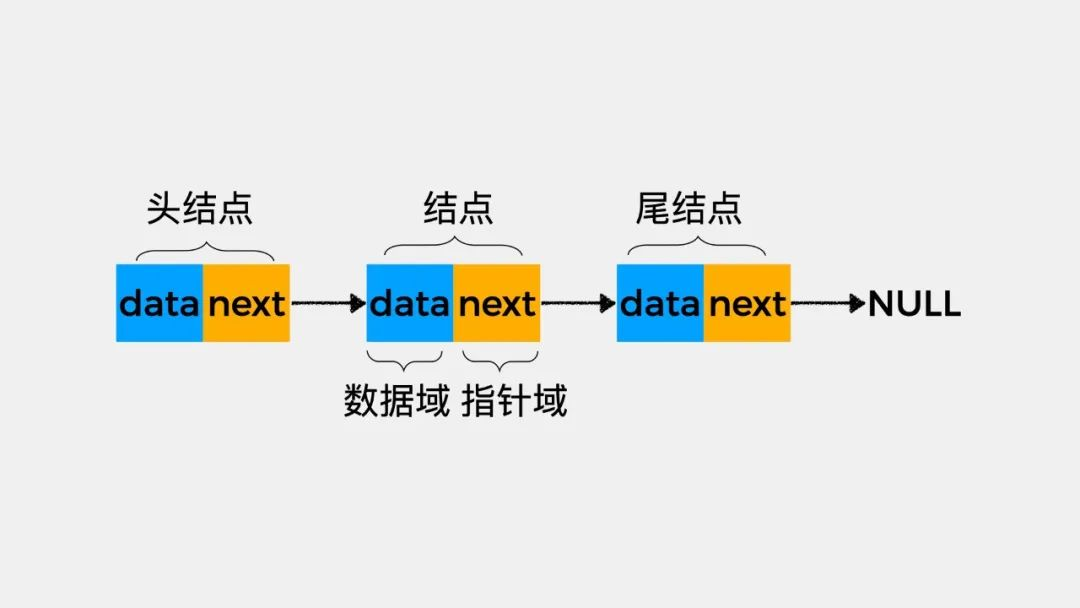
链表是一种线性数据结构,它由一系列节点组成,每个节点包含数据和指向下一个(或上一个)节点的指针。与数组相比,链表的优势是可以动态分配内存,插入和删除操作不需要移动大量元素。
10.2.1 单链表(Singly Linked List)
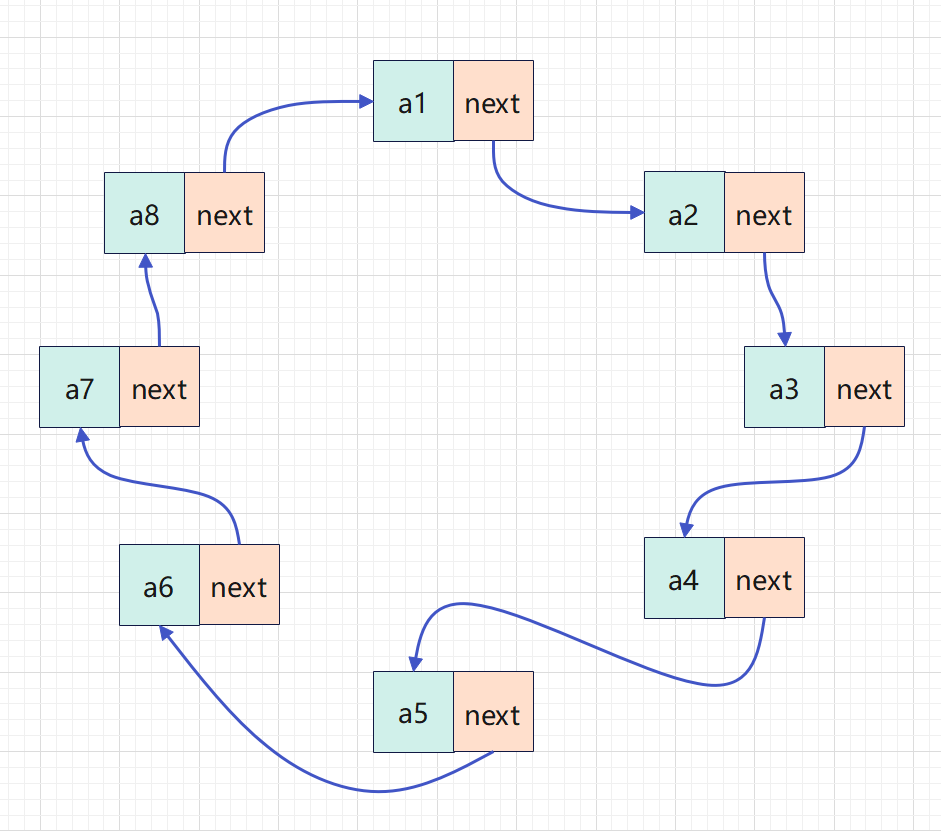
单链表是最简单的链表形式,每个节点只包含数据和一个指向下一个节点的指针。
单链表的基本操作:
- 初始化链表
- 插入节点(头部、尾部、指定位置)
- 删除节点(头部、尾部、指定值或位置)
- 查找节点
- 遍历链表
- 销毁链表
单链表的实现(C++ 代码):
#include <iostream>
#include <stdexcept>
using namespace std;
// 单链表节点结构
template <typename T>
struct Node {
T data; // 节点数据
Node* next; // 指向下一个节点的指针
// 构造函数
Node(T val) : data(val), next(nullptr) {}
};
// 单链表类
template <typename T>
class SinglyLinkedList {
private:
Node<T>* head; // 头指针,指向链表的第一个节点
int size; // 链表中节点的数量
public:
// 构造函数:初始化空链表
SinglyLinkedList() : head(nullptr), size(0) {}
// 析构函数:销毁链表,释放内存
~SinglyLinkedList() {
clear();
}
// 判断链表是否为空
bool isEmpty() const {
return size == 0;
}
// 获取链表的大小
int getSize() const {
return size;
}
// 在链表头部插入节点
void insertAtHead(T val) {
Node<T>* newNode = new Node<T>(val); // 创建新节点
newNode->next = head; // 新节点指向原来的头节点
head = newNode; // 头指针指向新节点
size++; // 节点数量加1
}
// 在链表尾部插入节点
void insertAtTail(T val) {
Node<T>* newNode = new Node<T>(val); // 创建新节点
if (isEmpty()) {
// 如果链表为空,新节点就是头节点
head = newNode;
} else {
// 否则,找到最后一个节点
Node<T>* current = head;
while (current->next != nullptr) {
current = current->next;
}
current->next = newNode; // 最后一个节点指向新节点
}
size++; // 节点数量加1
}
// 在指定位置插入节点(位置从0开始)
void insertAtPosition(int pos, T val) {
if (pos < 0 || pos > size) {
throw runtime_error("插入位置无效");
}
if (pos == 0) {
// 在头部插入
insertAtHead(val);
} else if (pos == size) {
// 在尾部插入
insertAtTail(val);
} else {
// 在中间位置插入
Node<T>* newNode = new Node<T>(val);
Node<T>* current = head;
// 找到要插入位置的前一个节点
for (int i = 0; i < pos - 1; ++i) {
current = current->next;
}
newNode->next = current->next; // 新节点指向当前节点的下一个节点
current->next = newNode; // 当前节点指向新节点
size++; // 节点数量加1
}
}
// 删除头部节点
void deleteAtHead() {
if (isEmpty()) {
throw runtime_error("链表为空,无法删除节点");
}
Node<T>* temp = head; // 保存头节点
head = head->next; // 头指针指向第二个节点
delete temp; // 释放原来头节点的内存
size--; // 节点数量减1
}
// 删除尾部节点
void deleteAtTail() {
if (isEmpty()) {
throw runtime_error("链表为空,无法删除节点");
}
if (size == 1) {
// 只有一个节点,直接删除头节点
delete head;
head = nullptr;
} else {
// 找到倒数第二个节点
Node<T>* current = head;
while (current->next->next != nullptr) {
current = current->next;
}
delete current->next; // 释放最后一个节点的内存
current->next = nullptr; // 倒数第二个节点的next设为nullptr
}
size--; // 节点数量减1
}
// 删除指定值的第一个节点
void deleteByValue(T val) {
if (isEmpty()) {
throw runtime_error("链表为空,无法删除节点");
}
// 特殊情况:要删除的是头节点
if (head->data == val) {
deleteAtHead();
return;
}
// 查找要删除节点的前一个节点
Node<T>* current = head;
while (current->next != nullptr && current->next->data != val) {
current = current->next;
}
// 如果找到了要删除的节点
if (current->next != nullptr) {
Node<T>* temp = current->next; // 保存要删除的节点
current->next = current->next->next; // 跳过要删除的节点
delete temp; // 释放内存
size--; // 节点数量减1
} else {
throw runtime_error("未找到要删除的值");
}
}
// 查找指定值的节点是否存在
bool search(T val) const {
Node<T>* current = head;
while (current != nullptr) {
if (current->data == val) {
return true; // 找到节点
}
current = current->next;
}
return false; // 未找到节点
}
// 获取指定位置的节点值(位置从0开始)
T getValueAt(int pos) const {
if (pos < 0 || pos >= size) {
throw runtime_error("位置无效");
}
Node<T>* current = head;
for (int i = 0; i < pos; ++i) {
current = current->next;
}
return current->data;
}
// 遍历并打印链表
void print() const {
if (isEmpty()) {
cout << "链表为空" << endl;
return;
}
cout << "链表元素:";
Node<T>* current = head;
while (current != nullptr) {
cout << current->data << " -> ";
current = current->next;
}
cout << "nullptr" << endl;
}
// 清空链表,释放所有节点的内存
void clear() {
while (!isEmpty()) {
deleteAtHead();
}
}
};
// 测试单链表的功能
int main() {
try {
SinglyLinkedList<int> list;
// 插入操作
list.insertAtHead(30);
list.insertAtHead(20);
list.insertAtHead(10);
list.print(); // 应输出:链表元素:10 -> 20 -> 30 -> nullptr
list.insertAtTail(40);
list.insertAtTail(50);
list.print(); // 应输出:链表元素:10 -> 20 -> 30 -> 40 -> 50 -> nullptr
list.insertAtPosition(2, 25);
list.print(); // 应输出:链表元素:10 -> 20 -> 25 -> 30 -> 40 -> 50 -> nullptr
// 查找操作
cout << "是否包含30:" << (list.search(30) ? "是" : "否") << endl; // 是
cout << "是否包含100:" << (list.search(100) ? "是" : "否") << endl; // 否
// 获取指定位置的值
cout << "位置3的值:" << list.getValueAt(3) << endl; // 30
// 删除操作
list.deleteAtHead();
list.print(); // 应输出:链表元素:20 -> 25 -> 30 -> 40 -> 50 -> nullptr
list.deleteAtTail();
list.print(); // 应输出:链表元素:20 -> 25 -> 30 -> 40 -> nullptr
list.deleteByValue(25);
list.print(); // 应输出:链表元素:20 -> 30 -> 40 -> nullptr
// 链表大小
cout << "链表大小:" << list.getSize() << endl; // 3
} catch (const exception& e) {
cout << "错误:" << e.what() << endl;
}
return 0;
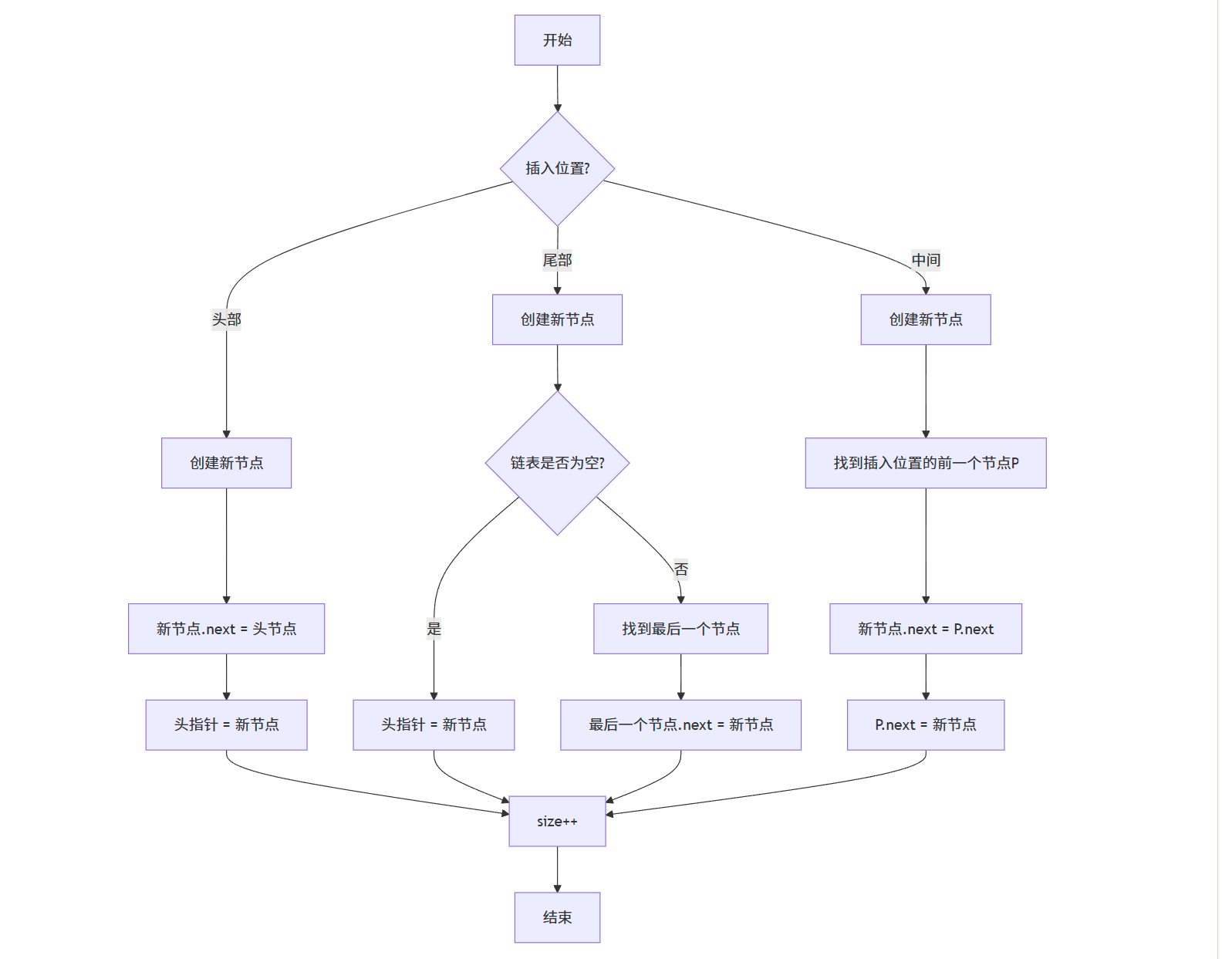
}单链表插入操作流程图:
10.2.2 双链表(Doubly Linked List)
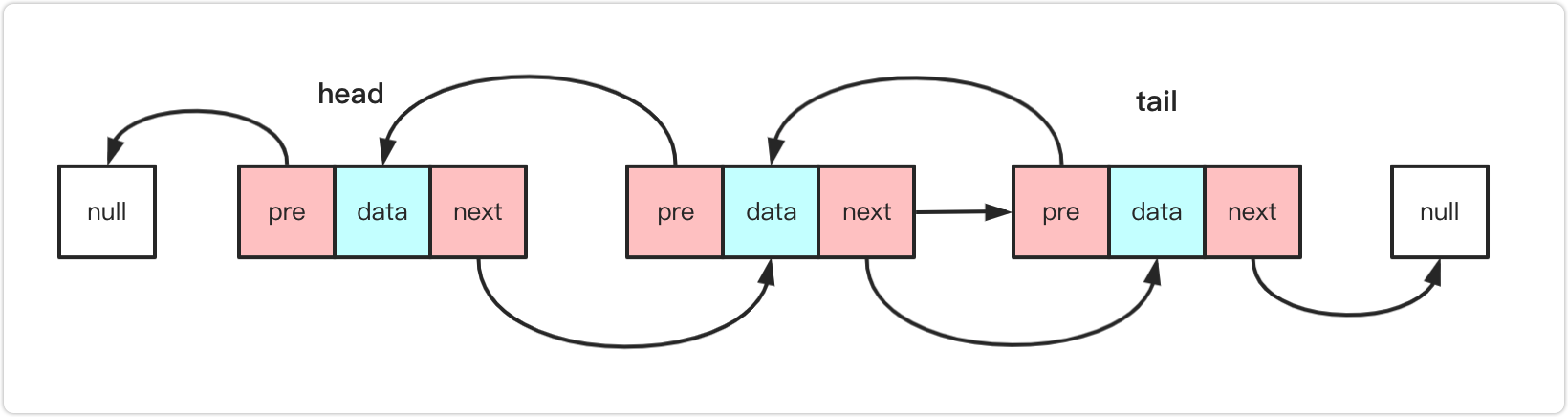
双链表与单链表的区别在于,每个节点不仅有指向下一个节点的指针,还有一个指向前一个节点 的指针。这使得双链表可以双向遍历,某些操作(如删除指定节点)更加高效。
双链表的实现(C++ 代码):
#include <iostream>
#include <stdexcept>
using namespace std;
// 双链表节点结构
template <typename T>
struct DNode {
T data; // 节点数据
DNode* prev; // 指向前一个节点的指针
DNode* next; // 指向下一个节点的指针
// 构造函数
DNode(T val) : data(val), prev(nullptr), next(nullptr) {}
};
// 双链表类
template <typename T>
class DoublyLinkedList {
private:
DNode<T>* head; // 头指针
DNode<T>* tail; // 尾指针
int size; // 链表中节点的数量
public:
// 构造函数:初始化空链表
DoublyLinkedList() : head(nullptr), tail(nullptr), size(0) {}
// 析构函数:销毁链表,释放内存
~DoublyLinkedList() {
clear();
}
// 判断链表是否为空
bool isEmpty() const {
return size == 0;
}
// 获取链表的大小
int getSize() const {
return size;
}
// 在链表头部插入节点
void insertAtHead(T val) {
DNode<T>* newNode = new DNode<T>(val); // 创建新节点
if (isEmpty()) {
// 如果链表为空,新节点既是头节点也是尾节点
head = newNode;
tail = newNode;
} else {
newNode->next = head; // 新节点的next指向原来的头节点
head->prev = newNode; // 原来头节点的prev指向新节点
head = newNode; // 头指针指向新节点
}
size++; // 节点数量加1
}
// 在链表尾部插入节点
void insertAtTail(T val) {
DNode<T>* newNode = new DNode<T>(val); // 创建新节点
if (isEmpty()) {
// 如果链表为空,新节点既是头节点也是尾节点
head = newNode;
tail = newNode;
} else {
newNode->prev = tail; // 新节点的prev指向原来的尾节点
tail->next = newNode; // 原来尾节点的next指向新节点
tail = newNode; // 尾指针指向新节点
}
size++; // 节点数量加1
}
// 在指定位置插入节点(位置从0开始)
void insertAtPosition(int pos, T val) {
if (pos < 0 || pos > size) {
throw runtime_error("插入位置无效");
}
if (pos == 0) {
// 在头部插入
insertAtHead(val);
} else if (pos == size) {
// 在尾部插入
insertAtTail(val);
} else {
// 在中间位置插入
DNode<T>* newNode = new DNode<T>(val);
DNode<T>* current;
// 优化:根据位置选择从头部还是尾部开始查找
if (pos <= size / 2) {
current = head;
for (int i = 0; i < pos; ++i) {
current = current->next;
}
} else {
current = tail;
for (int i = size - 1; i > pos; --i) {
current = current->prev;
}
}
// 插入新节点
newNode->prev = current->prev;
newNode->next = current;
current->prev->next = newNode;
current->prev = newNode;
size++; // 节点数量加1
}
}
// 删除头部节点
void deleteAtHead() {
if (isEmpty()) {
throw runtime_error("链表为空,无法删除节点");
}
DNode<T>* temp = head; // 保存头节点
if (size == 1) {
// 只有一个节点,头指针和尾指针都设为nullptr
head = nullptr;
tail = nullptr;
} else {
head = head->next; // 头指针指向第二个节点
head->prev = nullptr; // 新头节点的prev设为nullptr
}
delete temp; // 释放原来头节点的内存
size--; // 节点数量减1
}
// 删除尾部节点
void deleteAtTail() {
if (isEmpty()) {
throw runtime_error("链表为空,无法删除节点");
}
DNode<T>* temp = tail; // 保存尾节点
if (size == 1) {
// 只有一个节点,头指针和尾指针都设为nullptr
head = nullptr;
tail = nullptr;
} else {
tail = tail->prev; // 尾指针指向倒数第二个节点
tail->next = nullptr; // 新尾节点的next设为nullptr
}
delete temp; // 释放原来尾节点的内存
size--; // 节点数量减1
}
// 删除指定值的第一个节点
void deleteByValue(T val) {
if (isEmpty()) {
throw runtime_error("链表为空,无法删除节点");
}
DNode<T>* current = head;
while (current != nullptr && current->data != val) {
current = current->next;
}
if (current == nullptr) {
throw runtime_error("未找到要删除的值");
}
// 如果是头节点
if (current == head) {
deleteAtHead();
}
// 如果是尾节点
else if (current == tail) {
deleteAtTail();
}
// 中间节点
else {
current->prev->next = current->next;
current->next->prev = current->prev;
delete current;
size--;
}
}
// 正向遍历并打印链表
void printForward() const {
if (isEmpty()) {
cout << "链表为空" << endl;
return;
}
cout << "正向遍历:";
DNode<T>* current = head;
while (current != nullptr) {
cout << current->data << " <-> ";
current = current->next;
}
cout << "nullptr" << endl;
}
// 反向遍历并打印链表(双链表的优势)
void printBackward() const {
if (isEmpty()) {
cout << "链表为空" << endl;
return;
}
cout << "反向遍历:";
DNode<T>* current = tail;
while (current != nullptr) {
cout << current->data << " <-> ";
current = current->prev;
}
cout << "nullptr" << endl;
}
// 清空链表,释放所有节点的内存
void clear() {
while (!isEmpty()) {
deleteAtHead();
}
}
};
// 测试双链表的功能
int main() {
try {
DoublyLinkedList<int> list;
// 插入操作
list.insertAtHead(30);
list.insertAtHead(20);
list.insertAtHead(10);
list.printForward(); // 应输出:正向遍历:10 <-> 20 <-> 30 <-> nullptr
list.printBackward(); // 应输出:反向遍历:30 <-> 20 <-> 10 <-> nullptr
list.insertAtTail(40);
list.insertAtTail(50);
list.printForward(); // 应输出:正向遍历:10 <-> 20 <-> 30 <-> 40 <-> 50 <-> nullptr
list.insertAtPosition(2, 25);
list.printForward(); // 应输出:正向遍历:10 <-> 20 <-> 25 <-> 30 <-> 40 <-> 50 <-> nullptr
// 删除操作
list.deleteAtHead();
list.printForward(); // 应输出:正向遍历:20 <-> 25 <-> 30 <-> 40 <-> 50 <-> nullptr
list.deleteAtTail();
list.printForward(); // 应输出:正向遍历:20 <-> 25 <-> 30 <-> 40 <-> nullptr
list.deleteByValue(25);
list.printForward(); // 应输出:正向遍历:20 <-> 30 <-> 40 <-> nullptr
list.printBackward(); // 应输出:反向遍历:40 <-> 30 <-> 20 <-> nullptr
// 链表大小
cout << "链表大小:" << list.getSize() << endl; // 3
} catch (const exception& e) {
cout << "错误:" << e.what() << endl;
}
return 0;
}10.2.3 链表的综合应用案例
案例:两数相加(链表应用)
给你两个非空 的链表,表示两个非负的整数。它们每位数字都是按照逆序 的方式存储的,并且每个节点只能存储一位数字。请你将两个数相加,并以相同形式返回一个表示和的链表。
#include <iostream>
using namespace std;
// 定义链表节点
struct ListNode {
int val;
ListNode *next;
ListNode() : val(0), next(nullptr) {}
ListNode(int x) : val(x), next(nullptr) {}
ListNode(int x, ListNode *next) : val(x), next(next) {}
};
// 创建链表(从数组)
ListNode* createList(int arr[], int n) {
if (n == 0) return nullptr;
ListNode* head = new ListNode(arr[0]);
ListNode* current = head;
for (int i = 1; i < n; ++i) {
current->next = new ListNode(arr[i]);
current = current->next;
}
return head;
}
// 打印链表
void printList(ListNode* head) {
ListNode* current = head;
while (current != nullptr) {
cout << current->val;
if (current->next != nullptr) {
cout << " -> ";
}
current = current->next;
}
cout << endl;
}
// 两数相加
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
ListNode* dummyHead = new ListNode(0); // 哑节点,简化边界情况处理
ListNode* current = dummyHead;
int carry = 0; // 进位
// 遍历两个链表,直到两个链表都为空且没有进位
while (l1 != nullptr || l2 != nullptr || carry > 0) {
int sum = carry; // 先加上进位
// 加上l1当前节点的值(如果l1不为空)
if (l1 != nullptr) {
sum += l1->val;
l1 = l1->next; // 移动到l1的下一个节点
}
// 加上l2当前节点的值(如果l2不为空)
if (l2 != nullptr) {
sum += l2->val;
l2 = l2->next; // 移动到l2的下一个节点
}
carry = sum / 10; // 计算新的进位
current->next = new ListNode(sum % 10); // 当前位的和(取模10)
current = current->next; // 移动到下一个节点
}
ListNode* result = dummyHead->next;
delete dummyHead; // 释放哑节点的内存
return result;
}
int main() {
// 示例1:342 + 465 = 807
// 链表表示:2 -> 4 -> 3 和 5 -> 6 -> 4
int arr1[] = {2, 4, 3};
int arr2[] = {5, 6, 4};
ListNode* l1 = createList(arr1, 3);
ListNode* l2 = createList(arr2, 3);
cout << "l1: ";
printList(l1); // 2 -> 4 -> 3
cout << "l2: ";
printList(l2); // 5 -> 6 -> 4
ListNode* result = addTwoNumbers(l1, l2);
cout << "和: ";
printList(result); // 7 -> 0 -> 8
// 示例2:9999999 + 9999 = 10009998
// 链表表示:9->9->9->9->9->9->9 和 9->9->9->9
int arr3[] = {9, 9, 9, 9, 9, 9, 9};
int arr4[] = {9, 9, 9, 9};
ListNode* l3 = createList(arr3, 7);
ListNode* l4 = createList(arr4, 4);
cout << "\nl3: ";
printList(l3); // 9->9->9->9->9->9->9
cout << "l4: ";
printList(l4); // 9->9->9->9
ListNode* result2 = addTwoNumbers(l3, l4);
cout << "和: ";
printList(result2); // 8->9->9->9->0->0->0->1
return 0;
}10.3 指针和对象的实现
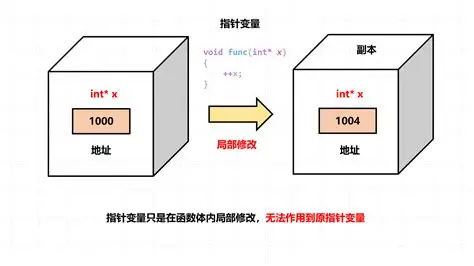
在许多编程语言中,指针是直接提供的,但在一些没有显式指针的语言中,我们需要模拟指针的功能。即使在有指针的语言中,了解指针的底层实现原理也有助于我们更好地理解数据结构的工作方式。
指针本质上是内存地址,我们可以用数组的索引来模拟指针。下面我们实现一个简单的 "内存管理器",用数组模拟内存空间,用索引模拟指针。
10.3.1 指针模拟实现(C++ 代码)
#include <iostream>
#include <vector>
#include <cstring>
using namespace std;
// 模拟内存块的状态
enum BlockStatus {
FREE, // 空闲
USED // 已使用
};
// 内存块结构
struct MemoryBlock {
BlockStatus status; // 块状态
int size; // 块大小(仅对空闲块有效)
char data[32]; // 数据区域(固定大小,简化实现)
int next; // 指向下一个块的"指针"(数组索引)
};
// 内存管理器类
class MemoryManager {
private:
vector<MemoryBlock> memory; // 模拟内存空间
const int BLOCK_SIZE; // 每个块的大小(字节)
int freeList; // 空闲块链表的头指针(索引)
public:
// 构造函数:初始化内存管理器
MemoryManager(int totalBlocks, int blockSize)
: BLOCK_SIZE(blockSize), freeList(0) {
// 初始化内存块
memory.resize(totalBlocks);
for (int i = 0; i < totalBlocks; ++i) {
memory[i].status = FREE;
memory[i].size = 1; // 每个空闲块初始大小为1个块
memory[i].next = i + 1; // 指向下一个块
memset(memory[i].data, 0, BLOCK_SIZE); // 初始化数据区域
}
memory[totalBlocks - 1].next = -1; // 最后一个块的next为-1(nullptr)
}
// 分配内存(模拟malloc)
int allocate(int numBlocks) {
if (numBlocks <= 0) return -1;
int prev = -1;
int current = freeList;
// 查找足够大的空闲块
while (current != -1) {
if (memory[current].size >= numBlocks) {
// 找到足够大的块
if (memory[current].size == numBlocks) {
// 块大小正好匹配,直接分配
if (prev == -1) {
freeList = memory[current].next;
} else {
memory[prev].next = memory[current].next;
}
} else {
// 块太大,需要分割
int splitBlock = current + numBlocks;
memory[splitBlock].status = FREE;
memory[splitBlock].size = memory[current].size - numBlocks;
memory[splitBlock].next = memory[current].next;
memory[current].size = numBlocks;
if (prev == -1) {
freeList = splitBlock;
} else {
memory[prev].next = splitBlock;
}
}
// 标记为已使用
memory[current].status = USED;
return current; // 返回分配的块的"指针"(索引)
}
// 继续查找下一个块
prev = current;
current = memory[current].next;
}
// 没有足够的内存
return -1;
}
// 释放内存(模拟free)
void deallocate(int ptr) {
if (ptr < 0 || ptr >= memory.size() || memory[ptr].status != USED) {
return; // 无效的指针
}
// 标记为空闲
memory[ptr].status = FREE;
// 将释放的块插入到空闲链表的头部
memory[ptr].next = freeList;
freeList = ptr;
// 合并相邻的空闲块(可选优化)
mergeFreeBlocks();
}
// 合并相邻的空闲块
void mergeFreeBlocks() {
int current = freeList;
while (current != -1 && memory[current].next != -1) {
int nextBlock = memory[current].next;
// 检查当前块和下一个块是否相邻
if (current + memory[current].size == nextBlock) {
// 合并两个块
memory[current].size += memory[nextBlock].size;
memory[current].next = memory[nextBlock].next;
} else {
// 不相邻,继续下一个块
current = nextBlock;
}
}
}
// 向指定内存地址写入数据
bool writeData(int ptr, const char* data, int dataSize) {
if (ptr < 0 || ptr >= memory.size() || memory[ptr].status != USED ||
dataSize > BLOCK_SIZE * memory[ptr].size) {
return false; // 无效的指针或数据太大
}
// 写入数据
int totalSize = 0;
int currentBlock = ptr;
while (totalSize < dataSize && currentBlock != -1) {
int blockDataSize = min(BLOCK_SIZE, dataSize - totalSize);
memcpy(memory[currentBlock].data, data + totalSize, blockDataSize);
totalSize += blockDataSize;
currentBlock++; // 下一个块(假设连续分配)
}
return totalSize == dataSize;
}
// 从指定内存地址读取数据
bool readData(int ptr, char* buffer, int bufferSize) {
if (ptr < 0 || ptr >= memory.size() || memory[ptr].status != USED || buffer == nullptr) {
return false; // 无效的指针
}
// 读取数据
int totalSize = 0;
int currentBlock = ptr;
int maxReadSize = BLOCK_SIZE * memory[ptr].size;
if (bufferSize > maxReadSize) {
bufferSize = maxReadSize; // 限制读取大小
}
while (totalSize < bufferSize && currentBlock != -1) {
int blockDataSize = min(BLOCK_SIZE, bufferSize - totalSize);
memcpy(buffer + totalSize, memory[currentBlock].data, blockDataSize);
totalSize += blockDataSize;
currentBlock++; // 下一个块(假设连续分配)
}
return totalSize == bufferSize;
}
// 打印内存状态
void printMemoryStatus() {
cout << "内存状态:" << endl;
for (int i = 0; i < memory.size(); ++i) {
cout << "块 " << i << ": ";
if (memory[i].status == USED) {
cout << "已使用,大小: " << memory[i].size << " 块";
} else {
cout << "空闲,大小: " << memory[i].size << " 块,下一个: " << memory[i].next;
}
cout << endl;
}
cout << "空闲链表头: " << freeList << endl << endl;
}
};
// 测试内存管理器
int main() {
// 创建一个有10个块,每个块32字节的内存管理器
MemoryManager manager(10, 32);
cout << "初始内存状态:" << endl;
manager.printMemoryStatus();
// 分配内存
int ptr1 = manager.allocate(2); // 分配2个块
cout << "分配2个块,指针: " << ptr1 << endl;
manager.printMemoryStatus();
int ptr2 = manager.allocate(3); // 分配3个块
cout << "分配3个块,指针: " << ptr2 << endl;
manager.printMemoryStatus();
// 写入数据
const char* message = "Hello, Memory Manager!";
bool writeSuccess = manager.writeData(ptr1, message, strlen(message) + 1);
cout << "写入数据" << (writeSuccess ? "成功" : "失败") << endl;
// 读取数据
char buffer[100];
bool readSuccess = manager.readData(ptr1, buffer, 100);
if (readSuccess) {
cout << "读取的数据: " << buffer << endl;
} else {
cout << "读取数据失败" << endl;
}
// 释放内存
manager.deallocate(ptr1);
cout << "释放指针 " << ptr1 << " 后的内存状态:" << endl;
manager.printMemoryStatus();
// 再次分配内存
int ptr3 = manager.allocate(4); // 分配4个块
cout << "分配4个块,指针: " << ptr3 << endl;
manager.printMemoryStatus();
return 0;
}10.3.2 指针模拟的应用场景
指针模拟在以下场景中非常有用:
- 内存受限的环境:如嵌入式系统,需要手动管理内存
- 自定义内存分配器:优化特定应用的内存使用
- 垃圾回收算法实现:跟踪对象引用关系
- 编程语言实现:在没有内置指针的语言中模拟指针功能
- 数据结构序列化:将包含指针的数据结构转换为可传输或存储的格式
10.4 有根树的表示

树是一种重要的非线性数据结构,它由 n(n≥0)个节点组成。有根树是指其中一个节点被指定为根节点,其余节点都是根节点的后代。
10.4.1 树的表示方法
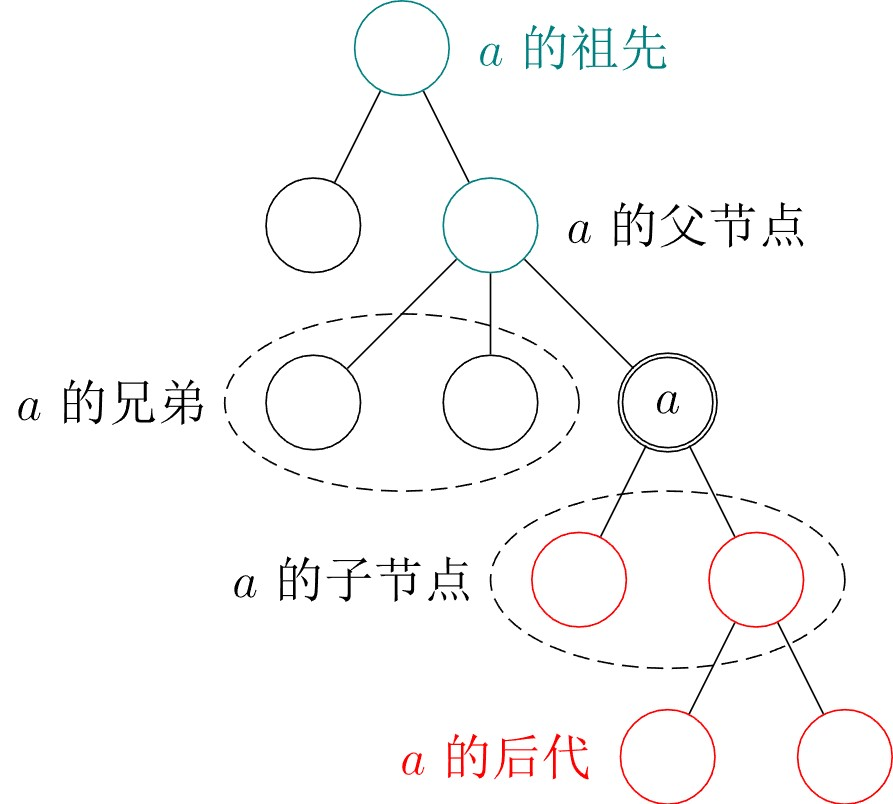
树有多种表示方法,各有优缺点,适用于不同的场景:
- 双亲表示法:每个节点存储其父节点的指针
- 孩子表示法:每个节点存储其所有子节点的指针列表
- 孩子 - 兄弟表示法:每个节点存储其第一个子节点和下一个兄弟节点的指针(最常用)
孩子 - 兄弟表示法(C++ 代码):
孩子 - 兄弟表示法是最灵活的树表示方法,它可以很方便地将树转换为二叉树,从而利用二叉树的算法。
cpp
#include <iostream>
#include <vector>
#include <string>
using namespace std;
// 树节点结构(孩子-兄弟表示法)
template <typename T>
struct TreeNode {
T data; // 节点数据
TreeNode* firstChild; // 指向第一个孩子节点
TreeNode* nextSibling;// 指向相邻的下一个兄弟节点
// 构造函数
TreeNode(T val) : data(val), firstChild(nullptr), nextSibling(nullptr) {}
};
// 树类
template <typename T>
class Tree {
private:
TreeNode<T>* root; // 根节点
// 递归销毁树
void destroy(TreeNode<T>* node) {
if (node == nullptr) return;
// 先销毁所有孩子节点
destroy(node->firstChild);
// 再销毁所有兄弟节点
destroy(node->nextSibling);
// 最后销毁当前节点
delete node;
}
// 递归前序遍历
void preOrder(TreeNode<T>* node, vector<T>& result) const {
if (node == nullptr) return;
// 先访问当前节点
result.push_back(node->data);
// 再遍历所有孩子节点(通过firstChild和nextSibling)
preOrder(node->firstChild, result);
preOrder(node->nextSibling, result);
}
// 递归后序遍历
void postOrder(TreeNode<T>* node, vector<T>& result) const {
if (node == nullptr) return;
// 先遍历所有孩子节点
postOrder(node->firstChild, result);
// 再访问当前节点
result.push_back(node->data);
// 最后遍历所有兄弟节点
postOrder(node->nextSibling, result);
}
// 递归查找节点
TreeNode<T>* findNode(TreeNode<T>* node, T val) const {
if (node == nullptr) return nullptr;
// 如果当前节点是要找的节点,返回它
if (node->data == val) return node;
// 先在孩子节点中查找
TreeNode<T>* found = findNode(node->firstChild, val);
if (found != nullptr) return found;
// 再在兄弟节点中查找
return findNode(node->nextSibling, val);
}
public:
// 构造函数
Tree() : root(nullptr) {}
// 带根节点的构造函数
Tree(T rootVal) : root(new TreeNode<T>(rootVal)) {}
// 析构函数
~Tree() {
destroy(root);
root = nullptr;
}
// 判断树是否为空
bool isEmpty() const {
return root == nullptr;
}
// 获取根节点
TreeNode<T>* getRoot() const {
return root;
}
// 设置根节点
void setRoot(T val) {
if (root != nullptr) {
destroy(root);
}
root = new TreeNode<T>(val);
}
// 给指定节点添加子节点
void addChild(TreeNode<T>* parent, T childVal) {
if (parent == nullptr) return;
TreeNode<T>* newNode = new TreeNode<T>(childVal);
// 如果父节点没有孩子,直接作为第一个孩子
if (parent->firstChild == nullptr) {
parent->firstChild = newNode;
} else {
// 否则,找到最后一个孩子,添加为其兄弟
TreeNode<T>* lastChild = parent->firstChild;
while (lastChild->nextSibling != nullptr) {
lastChild = lastChild->nextSibling;
}
lastChild->nextSibling = newNode;
}
}
// 查找值为val的节点
TreeNode<T>* find(T val) const {
return findNode(root, val);
}
// 前序遍历(根 -> 孩子 -> 兄弟)
vector<T> preOrderTraversal() const {
vector<T> result;
preOrder(root, result);
return result;
}
// 后序遍历(孩子 -> 根 -> 兄弟)
vector<T> postOrderTraversal() const {
vector<T> result;
postOrder(root, result);
return result;
}
// 打印遍历结果
void printTraversal(const vector<T>& traversal, const string& traversalName) const {
cout << traversalName << "遍历: ";
for (size_t i = 0; i < traversal.size(); ++i) {
cout << traversal[i];
if (i != traversal.size() - 1) {
cout << " -> ";
}
}
cout << endl;
}
};
// 测试树的功能
int main() {
// 创建一棵树,根节点为"根"
Tree<string> tree("根");
// 获取根节点
TreeNode<string>* root = tree.getRoot();
// 给根节点添加子节点
tree.addChild(root, "子节点1");
tree.addChild(root, "子节点2");
tree.addChild(root, "子节点3");
// 找到"子节点1",给它添加子节点
TreeNode<string>* child1 = tree.find("子节点1");
if (child1 != nullptr) {
tree.addChild(child1, "孙节点1-1");
tree.addChild(child1, "孙节点1-2");
}
// 找到"子节点3",给它添加子节点
TreeNode<string>* child3 = tree.find("子节点3");
if (child3 != nullptr) {
tree.addChild(child3, "孙节点3-1");
}
// 找到"孙节点3-1",给它添加子节点
TreeNode<string>* grandchild31 = tree.find("孙节点3-1");
if (grandchild31 != nullptr) {
tree.addChild(grandchild31, "曾孙节点3-1-1");
}
// 遍历树
vector<string> preOrder = tree.preOrderTraversal();
tree.printTraversal(preOrder, "前序");
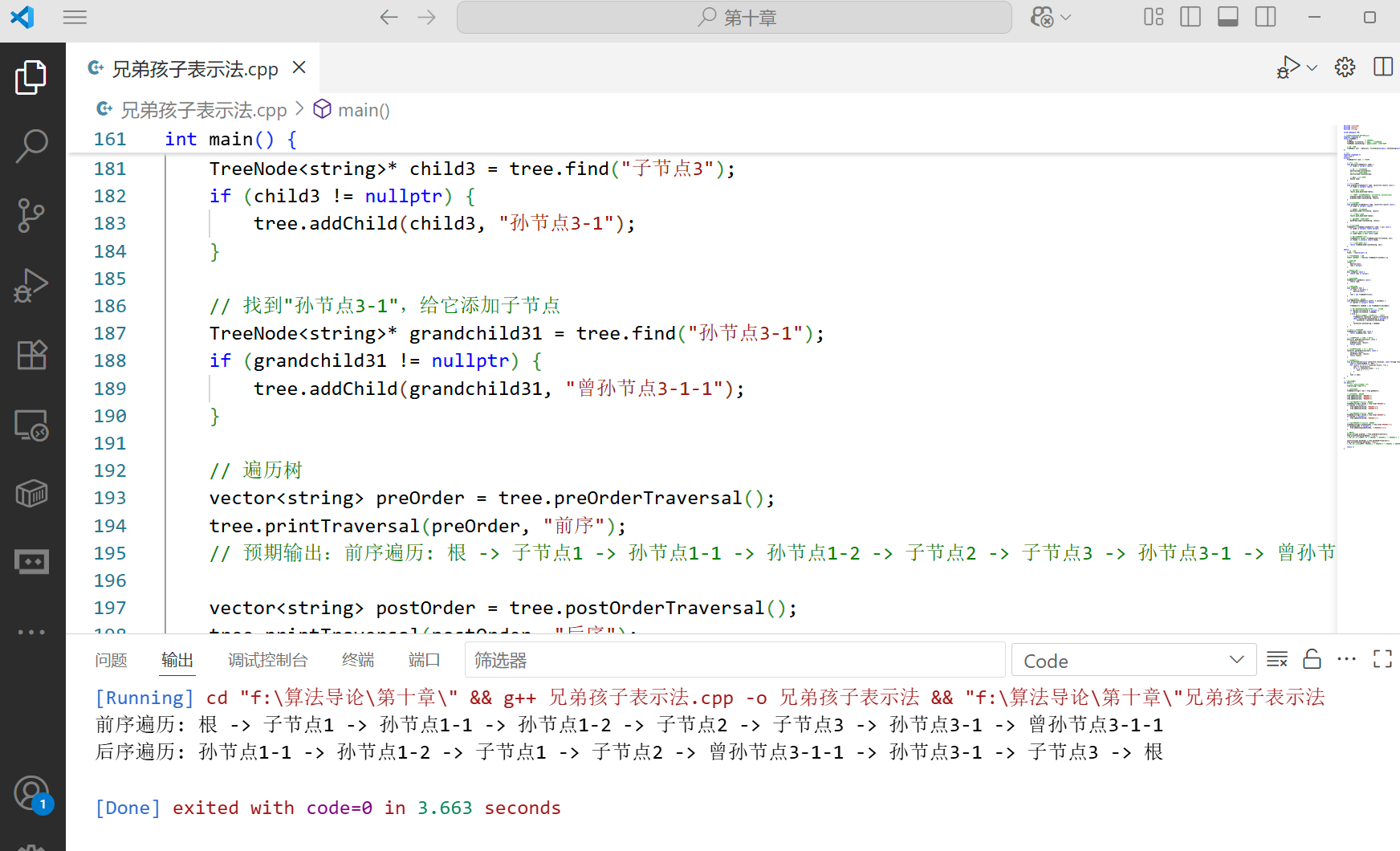
// 预期输出:前序遍历: 根 -> 子节点1 -> 孙节点1-1 -> 孙节点1-2 -> 子节点2 -> 子节点3 -> 孙节点3-1 -> 曾孙节点3-1-1
vector<string> postOrder = tree.postOrderTraversal();
tree.printTraversal(postOrder, "后序");
// 预期输出:后序遍历: 孙节点1-1 -> 孙节点1-2 -> 子节点1 -> 子节点2 -> 曾孙节点3-1-1 -> 孙节点3-1 -> 子节点3 -> 根
return 0;
}树的孩子 - 兄弟表示法类图:
@startuml
title 树的孩子-兄弟表示法类图
class TreeNode<T> {
- T data
- TreeNode<T>* firstChild
- TreeNode<T>* nextSibling
+ TreeNode(T val)
}
class Tree<T> {
- TreeNode<T>* root
- void destroy(TreeNode<T>* node)
- void preOrder(TreeNode<T>* node, vector<T>& result)
- void postOrder(TreeNode<T>* node, vector<T>& result)
- TreeNode<T>* findNode(TreeNode<T>* node, T val)
+ Tree()
+ Tree(T rootVal)
+ ~Tree()
+ bool isEmpty()
+ TreeNode<T>* getRoot()
+ void setRoot(T val)
+ void addChild(TreeNode<T>* parent, T childVal)
+ TreeNode<T>* find(T val)
+ vector<T> preOrderTraversal()
+ vector<T> postOrderTraversal()
+ void printTraversal(const vector<T>&, const string&)
}
Tree<T> "1" *-- "0..1" TreeNode<T> : has root
TreeNode<T> "1" *-- "0..1" TreeNode<T> : has firstChild
TreeNode<T> "1" *-- "0..1" TreeNode<T> : has nextSibling
@enduml10.4.2 树的综合应用案例
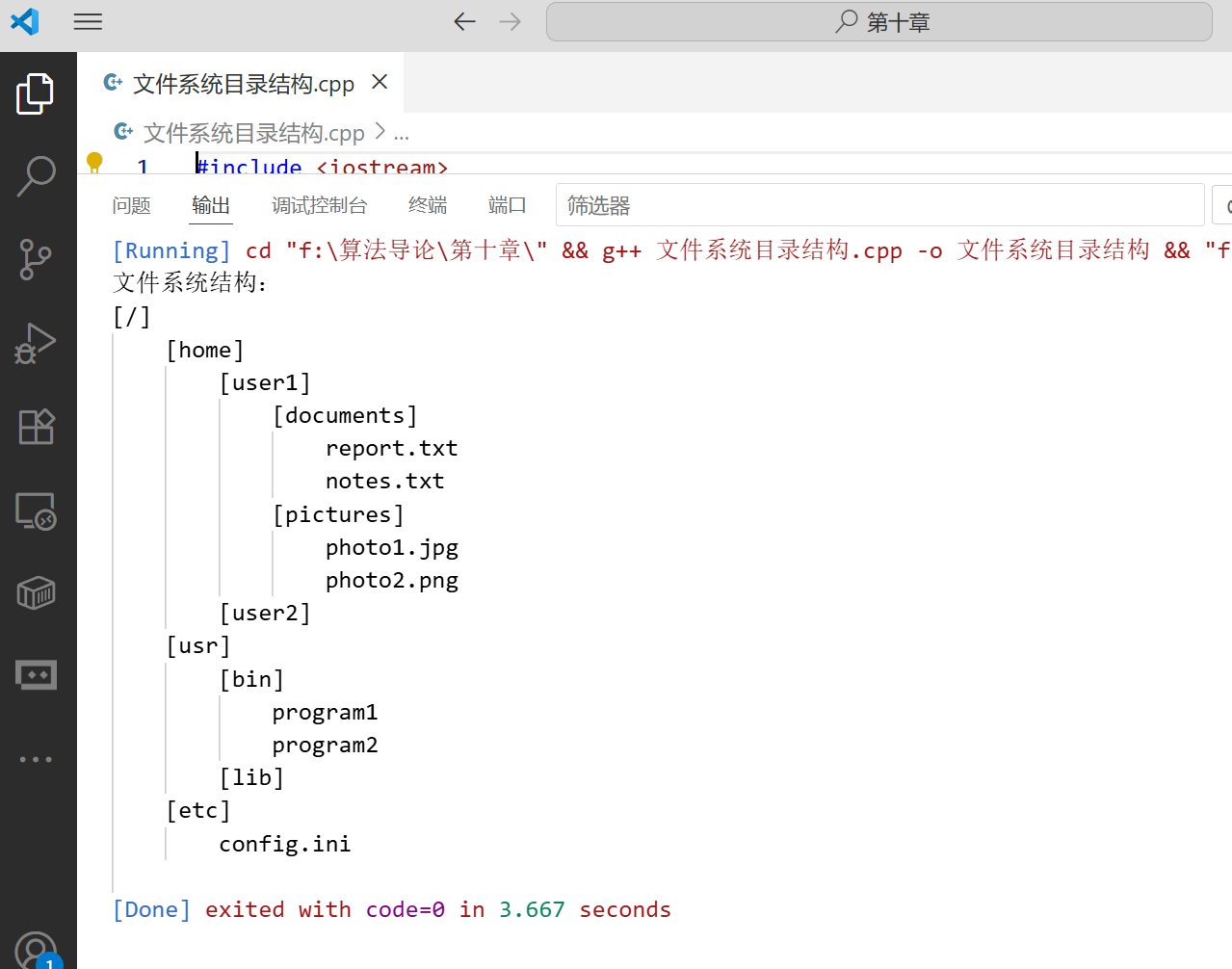
案例:文件系统目录结构(树的应用)
文件系统是树结构的典型应用,我们可以用树来模拟文件系统的目录结构:
#include <iostream>
#include <vector>
#include <string>
#include <iomanip>
using namespace std;
// 文件/目录节点
struct FileNode {
string name; // 名称
bool isDirectory; // 是否为目录
FileNode* firstChild; // 第一个子节点
FileNode* nextSibling;// 下一个兄弟节点
// 构造函数
FileNode(string n, bool isDir)
: name(n), isDirectory(isDir), firstChild(nullptr), nextSibling(nullptr) {}
};
// 文件系统类
class FileSystem {
private:
FileNode* root; // 根目录
// 递归销毁节点
void destroy(FileNode* node) {
if (node == nullptr) return;
// 先销毁所有子节点
destroy(node->firstChild);
// 再销毁所有兄弟节点
destroy(node->nextSibling);
// 最后销毁当前节点
delete node;
}
// 递归添加节点
bool addNode(FileNode* parent, FileNode* newNode) {
if (parent == nullptr || !parent->isDirectory) {
return false; // 父节点不存在或不是目录
}
// 如果父节点没有子节点,直接作为第一个子节点
if (parent->firstChild == nullptr) {
parent->firstChild = newNode;
} else {
// 否则,找到最后一个子节点,添加为其兄弟
FileNode* lastChild = parent->firstChild;
while (lastChild->nextSibling != nullptr) {
lastChild = lastChild->nextSibling;
}
lastChild->nextSibling = newNode;
}
return true;
}
// 递归查找节点
FileNode* findNode(FileNode* current, const string& name) {
if (current == nullptr) return nullptr;
// 如果当前节点是要找的节点,返回它
if (current->name == name) return current;
// 先在子节点中查找
FileNode* found = findNode(current->firstChild, name);
if (found != nullptr) return found;
// 再在兄弟节点中查找
return findNode(current->nextSibling, name);
}
// 递归打印目录结构
void printStructure(FileNode* node, int depth) const {
if (node == nullptr) return;
// 打印缩进
cout << setw(depth * 4) << "";
// 打印节点信息
if (node->isDirectory) {
cout << "[" << node->name << "]" << endl;
} else {
cout << node->name << endl;
}
// 先打印子节点
printStructure(node->firstChild, depth + 1);
// 再打印兄弟节点
printStructure(node->nextSibling, depth);
}
public:
// 构造函数
FileSystem() : root(new FileNode("/", true)) {}
// 析构函数
~FileSystem() {
destroy(root);
root = nullptr;
}
// 创建目录
bool createDirectory(const string& parentDir, const string& dirName) {
FileNode* parent = findNode(root, parentDir);
return addNode(parent, new FileNode(dirName, true));
}
// 创建文件
bool createFile(const string& parentDir, const string& fileName) {
FileNode* parent = findNode(root, parentDir);
return addNode(parent, new FileNode(fileName, false));
}
// 打印文件系统结构
void printFileSystem() const {
cout << "文件系统结构:" << endl;
printStructure(root, 0);
}
};
int main() {
FileSystem fs;
// 创建目录结构
fs.createDirectory("/", "home");
fs.createDirectory("/", "usr");
fs.createDirectory("/", "etc");
fs.createDirectory("home", "user1");
fs.createDirectory("home", "user2");
fs.createDirectory("user1", "documents");
fs.createDirectory("user1", "pictures");
fs.createDirectory("usr", "bin");
fs.createDirectory("usr", "lib");
// 创建文件
fs.createFile("documents", "report.txt");
fs.createFile("documents", "notes.txt");
fs.createFile("pictures", "photo1.jpg");
fs.createFile("pictures", "photo2.png");
fs.createFile("bin", "program1");
fs.createFile("bin", "program2");
fs.createFile("etc", "config.ini");
// 打印文件系统结构
fs.printFileSystem();
return 0;
}运行上述代码,将输出如下的文件系统结构: