第九章：空间网络模型（空间网络查询、数据模型、Connected、with Recursive、pgRouting）

第九章：空间网络模型

1. 基于位置的服务（Location Based Services）

• 位置（Location）：确定"我在哪里"。
• 目录（Directory）：查询"我周围有什么"。
• 路线（Routes）：规划"我如何到达那里"。

2. 空间网络分析（Spatial Network Analysis）

• 路径（Route）：从一个起点到一个或多个目的地。
• 分配（Allocation）：将一组服务点分配给一组客户。
• 站点选择（Site Selection）：在给定客户集和新服务点数量的情况下，选择最佳的站点位置。

3. 空间网络示例

• 道路、铁路、河流：这些是空间网络的典型例子。

空间网络的数据模型

1. 概念模型（Conceptual Model）

• 信息模型：实体关系图（Entity Relationship Diagrams）。
• 数学模型：图论（Graphs），包括道路转弯、河流、铁路等。

2. 逻辑数据模型（Logical Data Model）

• 抽象数据类型：传递闭包（Transitive Closure）。
• 自定义SQL语句 ：
  • SQL2：CONNECT子句用于SELECT语句。
  • SQL3：WITH RECURSIVE语句。

3. 物理数据模型（Physical Data Model）

• 存储结构和文件结构 ：
  • 邻接矩阵、邻接列表、规范化/非规范化表。
• 目标：最小化CRR（Cost, Redundancy, and Repetition）。

空间网络的查询处理

1. 主存查询处理

• 连通性：广度优先搜索、深度优先搜索。
• 最短路径：Dijkstra算法、A*算法。

2. 基于磁盘的查询处理

• 连通性策略：在SQL3中实现。
• 最短路径：分层路由算法。

3. pgRouting工具

• 主要功能 ：
  • pgr_createTopology：创建拓扑结构。
  • pgr_analyzeGraph：分析图结构。
  • pgr_nodeNetwork：节点网络处理。
  • pgr_dijkstra(text edges_sql, bigint start_vid, bigint end_vid, boolean directed:=true)：实现Dijkstra算法计算最短路径。

总结

空间网络模型及其应用涵盖了从基于位置的服务到复杂的网络分析。通过合理的数据模型设计和高效的查询处理算法，可以有效地解决诸如路径规划、资源分配和服务选址等问题。特别是利用SQL中的递归查询和专用的空间分析工具如pgRouting，能够极大地提升空间数据分析的能力和效率。

这段代码展示了 PostgreSQL 中使用 WITH RECURSIVE 进行图遍历查询的两个相关示例，重点是检测环路。

下面逐部分解析：

---

一、第一段代码（Example 4 完整版）

WITH RECURSIVE search_graph(id, link, data, depth, path, cycle) AS (
    SELECT g.id, g.link, g.data, 1,
           array[row(g.f1, g.f2)],
           false
    FROM graph g
    UNION ALL
    SELECT g.id, g.link, g.data, sg.depth + 1,
           path || row(g.f1, g.f2),
           row(g.f1, g.f2) = any(path)
    FROM graph g, search_graph sg
    WHERE g.id = sg.link AND NOT cycle
)
SELECT * FROM search_graph;

结构解析

1. WITH RECURSIVE search_graph(...) AS (...)

   定义一个递归公用表表达式，名为 search_graph，包含字段：

   • id：当前节点 ID（可能是 g.id）

   • link：指向的下一个节点 ID

   • data：节点数据

   • depth：递归深度

   • path：路径数组，记录已访问的 (f1, f2) 组合

   • cycle：布尔值，表示是否出现环路

2. 非递归项（初始查询）

   SELECT g.id, g.link, g.data, 1,
          array[row(g.f1, g.f2)],
          false
   FROM graph g

   • 从 graph 表取每一行作为起始点。

   • depth 初始化为 1。

   • path 初始化为一个数组，包含当前行的 row(g.f1, g.f2) 组合（row(...) 是 PostgreSQL 的行构造器）。

   • cycle 初始为 false。

3. 递归项

   SELECT g.id, g.link, g.data, sg.depth + 1,
          path || row(g.f1, g.f2),
          row(g.f1, g2) = any(path)
   FROM graph g, search_graph sg
   WHERE g.id = sg.link AND NOT cycle

   • 将上一次递归结果 sg 与原始 graph 表连接，条件是 g.id = sg.link，即沿着边往下走。

   • sg.depth + 1：深度加一。

   • path || row(g.f1, g2)：将当前节点的 (f1, f2) 追加到路径数组。

   • row(g.f1, g.f2) = any(path)：判断当前节点的 (f1, f2) 是否已在 path 中出现过，若出现过，则 cycle 为 true，否则 false。

   • AND NOT cycle：当 cycle 为 true 时停止该路径的递归，避免无限循环。

4. 最终查询

   SELECT * FROM search_graph;

   输出递归过程中的所有行。

---

二、第二段代码（简化版，有循环风险）

WITH RECURSIVE search_graph(id, link, data, depth) AS (
    SELECT g.id, g.link, g.data, 1
    FROM graph g
    UNION ALL
    SELECT g.id, g.link, g.data, sg.depth + 1
    FROM graph g, search_graph sg
    WHERE g.id = sg.link
)
SELECT * FROM search_graph;

解析

1. 没有 path 和 cycle 检测机制。

2. 如果图中有环（link 指向已访问过的节点），则递归会无限循环直到超出递归深度限制。

3. 注释提到：

   如果 link 关系包含环，这个查询会死循环。

   将 UNION ALL 改成 UNION 并不能消除循环，因为 depth 不同，UNION 认为它们是不同的行。

---

三、关键点总结

1. 环路检测原理

   第一段代码使用 path 数组记录行的字段组合 (f1, f2)，并用 cycle 布尔值判断是否重复，通过 AND NOT cycle 提前终止循环路径。

2. ROW(...) 与 ANY(path)
ROW(g.f1, g.f2) 构造一个复合类型值（或元组），= ANY(path) 检查该值是否在数组 path 中。

3. 递归停止条件

   ① 没有满足 g.id = sg.link 的行；

   ② 遇到 cycle = true 的行不再递归。

一、数据结构示例

假设 graph 表有如下数据：

| id | link | data | f1 | f2 |
|----|------|--------|--------|--------|------------------------|
| A | B | d1 | x1 | y1 |
| B | C | d2 | x2 | y2 |
| C | D | d3 | x3 | y3 |
| D | B | d4 | x2 | y2 | ← 这里创建了环 (B→C→D→B) |

二、递归执行过程图

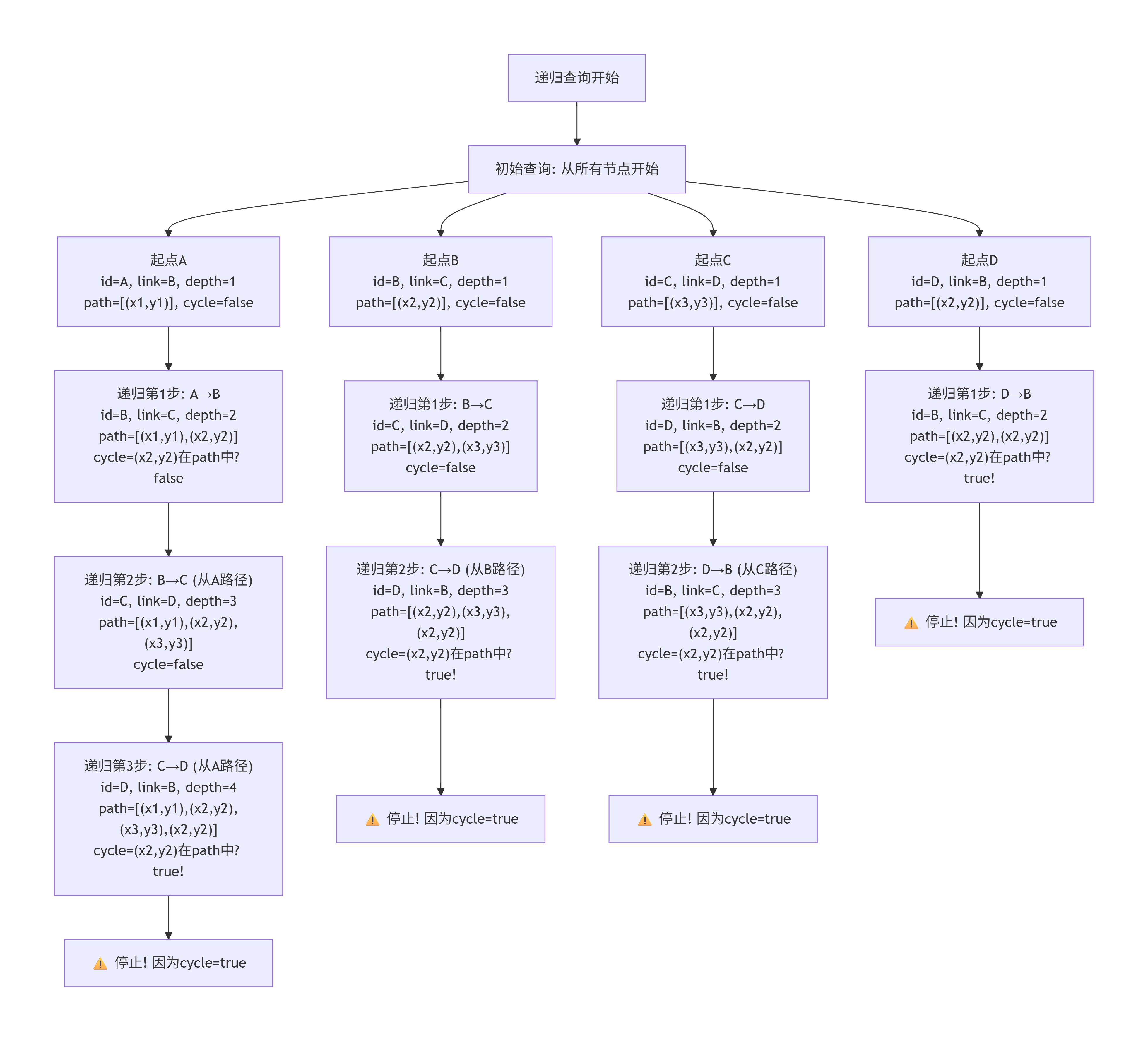
三、关键步骤详细说明

第0轮（初始查询）：

SELECT 'A', 'B', 'd1', 1, array[('x1','y1')], false
SELECT 'B', 'C', 'd2', 1, array[('x2','y2')], false
SELECT 'C', 'D', 'd3', 1, array[('x3','y3')], false
SELECT 'D', 'B', 'd4', 1, array[('x2','y2')], false

第1轮递归（从起点A出发）：

text

当前: sg = (A, B, d1, 1, [(x1,y1)], false)
连接: graph中 id = 'B' 的行是 (B, C, d2, x2, y2)
结果:
  id = 'B'
  link = 'C'
  data = 'd2'
  depth = 2
  path = [(x1,y1)] || (x2,y2) = [(x1,y1), (x2,y2)]
  cycle = (x2,y2) IN [(x1,y1)]? = false

第1轮递归（从起点D出发）：

text

当前: sg = (D, B, d4, 1, [(x2,y2)], false)
连接: graph中 id = 'B' 的行是 (B, C, d2, x2, y2)
结果:
  id = 'B'
  link = 'C'
  data = 'd2'
  depth = 2
  path = [(x2,y2)] || (x2,y2) = [(x2,y2), (x2,y2)]
  cycle = (x2,y2) IN [(x2,y2)]? = true! ⚠️ 检测到环!

四、最终输出结果示例

| id | link | data | depth | path | cycle |
|-------|-------|--------|-------|-----------------------------------------|-----------|------------------|
| A | B | d1 | 1 | [(x1,y1)] | false |
| B | C | d2 | 1 | [(x2,y2)] | false |
| C | D | d3 | 1 | [(x3,y3)] | false |
| D | B | d4 | 1 | [(x2,y2)] | false |
| B | C | d2 | 2 | [(x1,y1),(x2,y2)] | false | ← 从A→B |
| C | D | d2 | 2 | [(x2,y2),(x3,y3)] | false | ← 从B→C |
| D | B | d3 | 2 | [(x3,y3),(x2,y2)] | false | ← 从C→D |
| B | C | d2 | 2 | [(x2,y2),(x2,y2)] | true | ← 从D→B（检测到环） |
| C | D | d2 | 3 | [(x1,y1),(x2,y2),(x3,y3)] | false | ← 从A→B→C |
| D | B | d3 | 3 | [(x2,y2),(x3,y3),(x2,y2)] | true | ← 从B→C→D |
| B | C | d2 | 3 | [(x3,y3),(x2,y2),(x2,y2)] | true | ← 从C→D→B |
| D | B | d3 | 4 | [(x1,y1),(x2,y2),(x3,y3),(x2,y2)] | true | ← 从A→B→C→D |

五、环路检测机制总结

1. 检测依据 ：通过检查 (f1, f2) 的组合是否在 path 数组中重复出现

2. 停止条件 ：当 cycle = true 时，AND NOT cycle 会阻止该路径继续递归

3. 重要细节 ：检测的是字段值组合 的重复，而不是节点ID的重复（如果只检测节点ID，只需 id = ANY(path) 即可）

这种机制特别适用于需要根据多个字段判断是否形成环路的情况，例如在复合键图遍历中。