卷积,一个让cv新手又爱又恨的东西。爱的是他的效果真的很好,恨的是他到底在卷什么呢?今天三水儿就从数学原理,到传统视觉,到卷积神经网络带你看看这个他到底在卷点什么。
1. 从数学原理出发
1.1 公式
当一个函数翻转并划过另一个函数的时候,两个函数在重叠的区域的乘积的积分或求和。
连续卷积:
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> ( f ∗ g ) ( t ) = i n t − ∞ ∞ f ( τ ) ⋅ g ( t − τ ) d τ (f * g)(t) = int_{-\infty}^{\infty} f(\tau) \cdot g(t - \tau) d\tau </math>(f∗g)(t)=int−∞∞f(τ)⋅g(t−τ)dτ
其中:
- f (t): 输入信号(例如音频、传感器数据)
- g (t): 核函数(也称为滤波器、冲激响应、点扩散函数)
- t: 时间(或空间位置)
- τ: 积分变量("滑动"核的时间偏移)
- g (t −τ ): 表示对函数 g 进行翻转(围绕纵轴)和平移 t。
离散卷积:
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> ( f ∗ g ) [ n ] = ∑ k = − ∞ ∞ f [ k ] ⋅ g [ n − k ] (f * g)[n] = \sum_{k=-\infty}^{\infty} f[k] \cdot g[n - k] </math>(f∗g)[n]=k=−∞∑∞f[k]⋅g[n−k]
其中:
- <math xmlns="http://www.w3.org/1998/Math/MathML"> f [ n ] 和 g [ n ] f[n] 和 g[n] </math>f[n]和g[n] 是两个离散序列
二维卷积(图像处理):
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> ( I ∗ K ) [ i , j ] = ∑ m ∑ n I [ m , n ] ⋅ K [ i − m , j − n ] (I * K)[i, j] = \sum_{m} \sum_{n} I[m, n] \cdot K[i - m, j - n] </math>(I∗K)[i,j]=m∑n∑I[m,n]⋅K[i−m,j−n]
即将卷积核反转后再做滑动点积
其中:
- <math xmlns="http://www.w3.org/1998/Math/MathML"> I [ m , n ] I[m, n] </math>I[m,n]:输入图像像素值。
- <math xmlns="http://www.w3.org/1998/Math/MathML"> K [ i − m , j − n ] K[i - m, j - n] </math>K[i−m,j−n]:卷积核(或滤波器),通常是较小的矩阵(如 3x3, 5x5),翻转后在图像上滑动。
在这里对于从事CV的朋友们,我们要关心的是离散卷积和**二维卷积。**离散卷积帮助我们理解原理,二维卷积是我们在图像处理中要使用的内容。
1.2 积
首先我们来理解积,也就是点乘,这个运算其实一直包含在卷积里。点乘很简单,我们在中学就学习过,对应位置相乘然后再相加。但我们忽略了其中两个很重要的应用。
- 点乘可以衡量两个向量的相似程度,点乘结果越大越相似。
- 点乘可以起到滤波的作用,即提取我们关心的内容。
相似度
首先我们来看衡量相似度:
python
# 1. 定义二维向量
ref_vec_2d = np.array([3, 2])
vec_a_2d = np.array([2.8, 1.9])
vec_b_2d = np.array([2, 3])
vec_c_2d = np.array([-1, 1.5])
dot_a_2d = np.dot(ref_vec_2d, vec_a_2d)
dot_b_2d = np.dot(ref_vec_2d, vec_b_2d)
dot_c_2d = np.dot(ref_vec_2d, vec_c_2d)
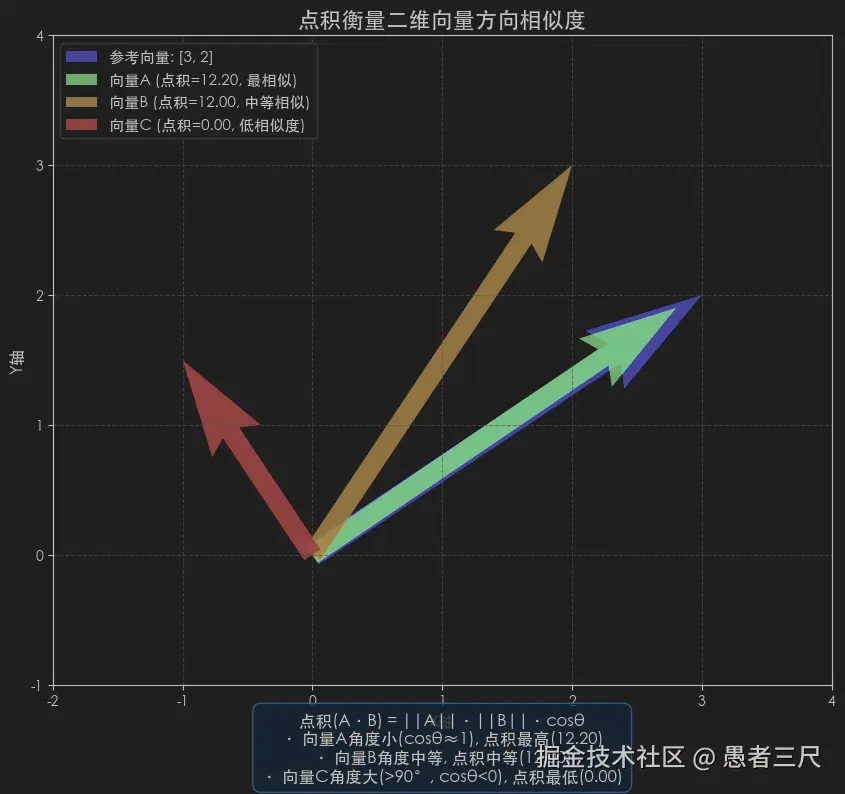
print(f"向量A点积: {dot_a_2d:.2f}") # 向量A点积: 12.20
print(f"向量B点积: {dot_b_2d:.2f}") # 向量B点积: 12.00
print(f"向量C点积: {dot_c_2d:.2f}") # 向量C点积: 0.00我们可以看出向量A与目标向量ref的点积更大,也即A与ref更加相似,反应到图像中我们可以看到如下图,A与参考向量几乎重叠。
我们再换一种展现方式,我们将向量变成平面上的离散点,用线将各点连接,可以很直观的看到各向量的相似度。
python
ref_vec_7d = np.array([0.8, 1.2, 1.0, 1.5, 0.7, 1.3, 1.1])
vec_a_7d = np.array([0.9, 1.3, 1.1, 1.4, 0.8, 1.2, 1.0])
vec_b_7d = np.array([0.6, 0.9, 0.8, 1.0, 0.9, 0.7, 1.3])
vec_c_7d = np.array([-0.7, 0.8, -1.2, 1.1, 0.9, -0.5, -1.0])
# 2. 计算点积
dot_a_7d = np.dot(ref_vec_7d, vec_a_7d)
dot_b_7d = np.dot(ref_vec_7d, vec_b_7d)
dot_c_7d = np.dot(ref_vec_7d, vec_c_7d)
print(f"向量A点积: {dot_a_7d:.2f}") # 向量A点积: 8.70
print(f"向量B点积: {dot_b_7d:.2f}") # 向量B点积: 6.83
print(f"向量C点积: {dot_c_7d:.2f}") # 向量C点积: -0.27如下图:
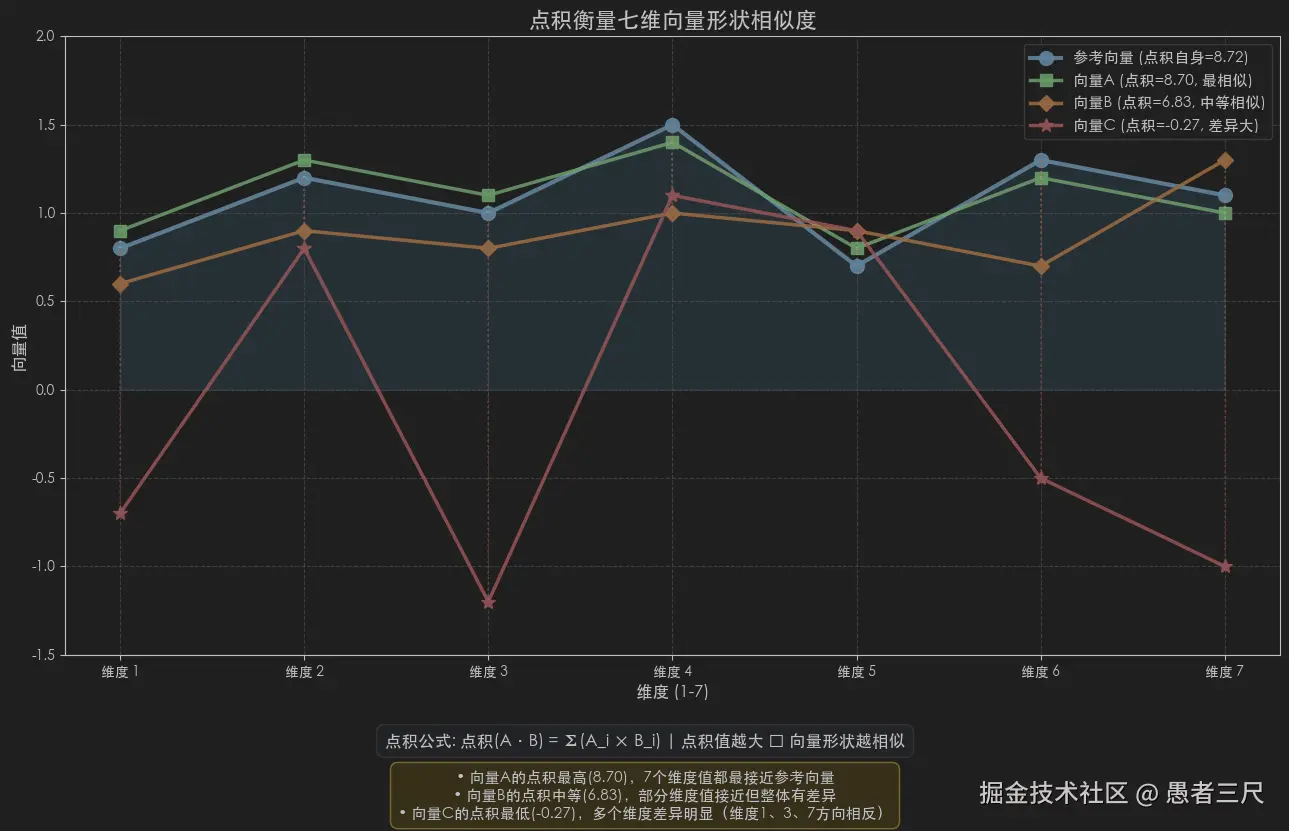
我们可以很明显的看出参考向量和向量A有一样的变化趋势。
滤波
首先我们来理解滤波的含义。所谓滤波就是过滤掉你不想要的东西,保留下你想要的东西,但最终的结果他还是个波。不能变成馒头。
首先让我们来理解过滤,卷积核其实就相当于一个没有总数限制的权制,我们在对一个序列中的部分数据做加权求和。
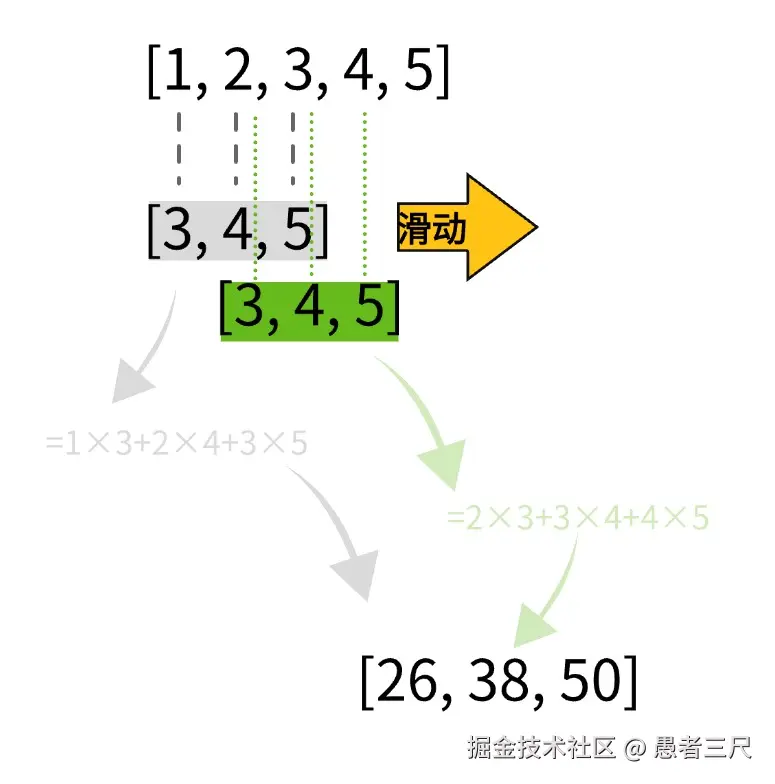
我们向后滑动,就会对每个位置的相关数据做了增强或者抑制。经过滑动我们就得到了一个被"卷积"过滤过的数据。
1.2 卷
积讲完了,我们接着将卷,卷体现在我们要将卷积核进行翻转后求点积。那么为什么要翻转呢?从滤波的角度来解释,波实际是一个时序的数据,即其当前的输出取决于过去的输入。我们翻转卷积就是在实现这种时间的反演关系,从而过滤掉我们不想要的波。
但这个卷在图像处理领域,其实体现的并不明显。在传统图像处理的卷积中,我们一般遵循数学上的定义对卷积核进行翻转;但在深度学习中我们就不会做这个翻转了,我们主要利用的实际上是积强化的性质。由于我们主要是做图像处理的这里就不深入介绍了。
2.传统图像处理中的卷积
接下来就让我们了解几个传统图像处理中的卷积核,来验证一下这些理论。有请我们这次的受害嘉宾,来自于铁甲小宝中的鲨鱼辣椒。

下面我会使用几个卷积核分别对这张图片进行卷积处理。大家在看卷积核介绍的时候可以先思考一下这个图片接下来会变成什么样子,注意传统图像处理中卷积核是要翻转的。
2.1 Sobel核
Sobel核的样子如下:
python
# 创建Sobel边缘检测核(水平方向)
sobel_kernel_x = np.array([
[-1, 0, 1],
[-2, 0, 2],
[-1, 0, 1]
], dtype=np.float32)
# 创建Sobel边缘检测核(垂直方向)
sobel_kernel_y = np.array([
[-1, -2, -1],
[0, 0, 0],
[1, 2, 1]
], dtype=np.float32)其主要特性是:
- 权重分布:正负权重交替,形成梯度
- 效果:突出图像中的边缘和轮廓
- 应用:边缘检测、特征提取、图像分割
我们将鲨鱼辣椒转为灰度图片,然后对其进行分别应用Sobel水平和垂直核后可以看到我们获得了其的边缘图像。
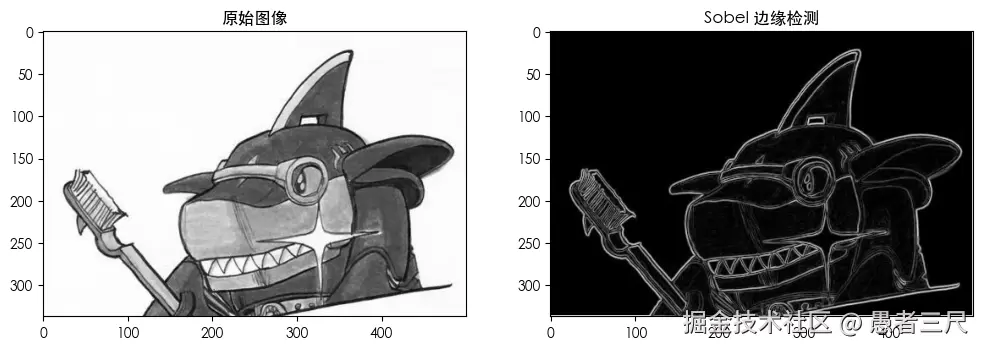
效果:
- 图像中的边缘和轮廓被强化
- 边界清晰可见
- 纹理细节被抑制
2.2 高斯模糊核
高斯模糊核一般为:
python
# 7*7 的高斯模糊核
[[0.0013 0.0041 0.0079 0.0099 0.0079 0.0041 0.0013]
[0.0041 0.0124 0.0241 0.0301 0.0241 0.0124 0.0041]
[0.0079 0.0241 0.047 0.0587 0.047 0.0241 0.0079]
[0.0099 0.0301 0.0587 0.0733 0.0587 0.0301 0.0099]
[0.0079 0.0241 0.047 0.0587 0.047 0.0241 0.0079]
[0.0041 0.0124 0.0241 0.0301 0.0241 0.0124 0.0041]
[0.0013 0.0041 0.0079 0.0099 0.0079 0.0041 0.0013]]其主要特性为:
- 权重分布:中心权重最大,向外递减
- 效果:抑制高频噪声,保留低频信息
- 应用:图像降噪,预处理、背景平滑
同样我们将鲨鱼辣椒变成灰度图,然后分别用33、55、7*7的核对他进行卷积,我们可以明显的发现高斯核越大,鲨鱼辣椒越模糊。

效果:
- 图像中的细节和纹理被平滑处理
- 主体轮廓和主要特征得到保留
- 噪点和微小纹理被有效抑制
2.3 拉普拉斯锐化核
拉普拉斯锐华核为:
python
# 使用的拉普拉斯核 (4-neighbor):
[[ 0. 1. 0.]
[ 1. -4. 1.]
[ 0. 1. 0.]]其主要特性为:
- 权重分布:中心高权重,周围负权重
- 效果:增强图像中的高频细节
- 应用:图像锐化、细节增强、纹理分析
这次我们不让鲨鱼辣椒变成灰度了,保留他的色彩,我们可以看出在添加了之后鲨鱼辣椒的所有边缘都变得更加清晰了。

效果:
- 图像中的细节和纹理被平滑处理
- 主体轮廓和主要特征得到保留
- 噪点和微小纹理被有效抑制
3. 卷积神经网络
在卷积神经网络中,我们一般只设定卷积核的大小,然后通过返现传播让卷积核根据数据自己拟合出来最适合的卷积核。
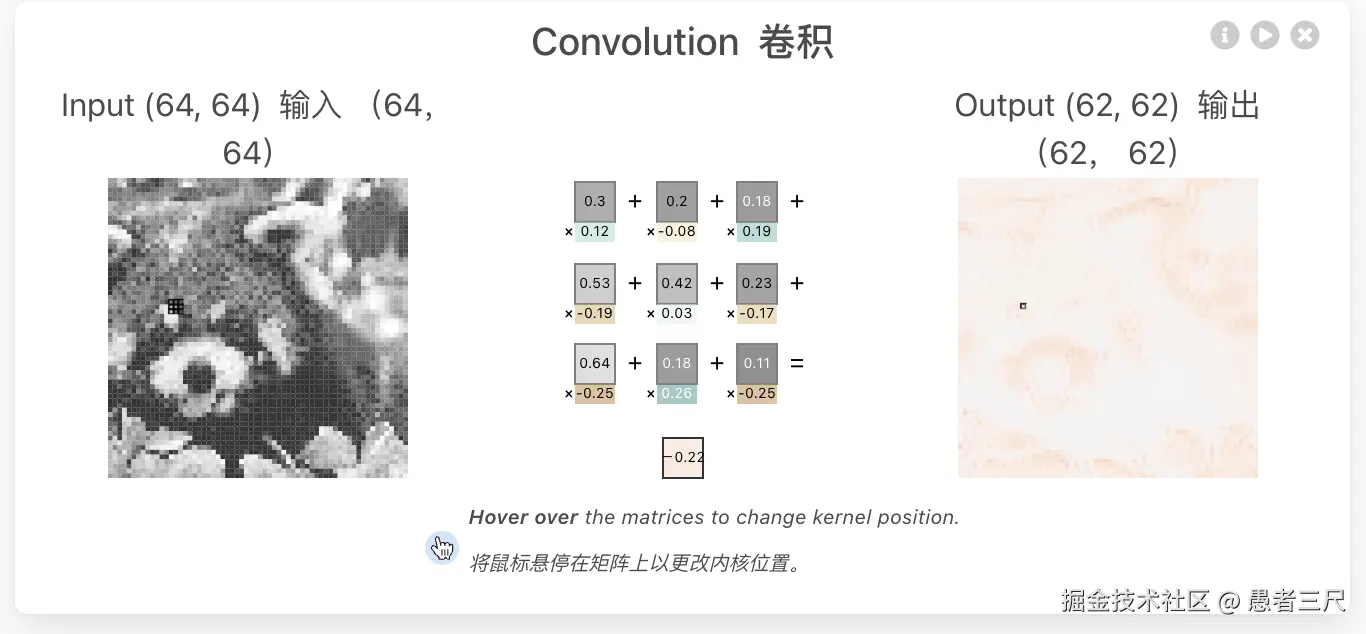
所以在这里我们只放一张大致的示意图,向要仔细查看的可以到CNN Explainer中去自行查看。
4. 总结
我们今天从数学的原理出发,理解了卷积为什么叫卷积以及积在现实中的一些作用,也就是找相似和过滤。之后我们带着这个理解了解了传统中的几个卷积核以及神经网络的卷积核。所以在图像处理中我们的卷积核的主要作用就是帮助我们进行特征提取,特征筛选。好啦今天的文章就到这里了。愿我们一起变得更强。
5. 推荐阅读
卷积核相关的论文
- 《Deformable Convolutional Networks》
- DOI: 10.1007/978-3-319-46466-4_28
- 《Large Kernel Matters - Improve Semantic Segmentation by Global Convolutional Network》
- DOI: 10.1109/CVPR.2017.189
- 《Scaling up Kernels in 3D CNNs》
- DOI: 10.48550/arXiv.2206.10555
图书推荐
- 《数字图像处理》(冈萨雷斯)
- 《Python图像处理实战》
- 《OpenCV 4计算机视觉项目实践(原书第2版)》
参考链接
【官方双语】那么......什么是卷积?_哔哩哔哩_bilibili
一个视频20分钟讲透:卷积底层数学逻辑是什么?为什么要卷?不卷行不行?它竟然和傅里叶变换拉普拉斯变换小波变换同宗同源?计算实例,应用演示!_哔哩哔哩_bilibili
文章首发gzh【破茧plan】,欢迎关注。