找到图中代价最低路径的问题,可以用路径中边权重总和来衡量,这与现实中各种路径规划和优化任务非常相似。比如,我们可能想规划两座城市间卡车的运输路线,使燃料总成本最小化。本章将讨论从指定起点出发,寻找最低成本路径的算法。
虽然这个问题通常称为"最短路径问题",但更准确的说法应该是"最低成本路径问题",因为路径的成本不一定是距离的函数。例如,本章还会考虑允许负权边的情况。本文中"最短路径"和"最低成本路径"两个术语可以互换使用,它们的表达和实现方法相同。
本章介绍三种寻找最短路径的算法。首先是迪杰斯特拉(Dijkstra)算法,它和前面章节的搜索算法类似,从起点节点向外探索。然后是贝尔曼-福特(Bellman-Ford)算法,通过迭代考虑每条边不断优化路径。最后是弗洛伊德-沃舍尔(Floyd-Warshall)算法,能找到所有节点对之间的最短路径。
最低成本路径的定义
在深入算法之前,我们先正式定义"最低成本路径"的含义。回顾第三章,路径的总成本是路径上所有边权重的和。对路径 <math xmlns="http://www.w3.org/1998/Math/MathML"> p = [ e 0 , e 1 , ... , e k ] p = [e_0, e_1, \ldots, e_k] </math>p=[e0,e1,...,ek],定义成本为:
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> PathCost ( p ) = ∑ i = 0 k e i . weight \text{PathCost}(p) = \sum_{i=0}^k e_i.\text{weight} </math>PathCost(p)=i=0∑kei.weight
我们定义从给定起点 <math xmlns="http://www.w3.org/1998/Math/MathML"> u u </math>u 到终点 <math xmlns="http://www.w3.org/1998/Math/MathML"> v v </math>v 的最短路径为一条边序列 <math xmlns="http://www.w3.org/1998/Math/MathML"> p = [ e 0 , e 1 , ... , e k ] p = [e_0, e_1, \ldots, e_k] </math>p=[e0,e1,...,ek],满足起点为 <math xmlns="http://www.w3.org/1998/Math/MathML"> u u </math>u,终点为 <math xmlns="http://www.w3.org/1998/Math/MathML"> v v </math>v,且路径成本最小:
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> ShortestPath ( u , v ) = min p PathCost ( p ) such that e 0 . from_node = u and e k . to_node = v \text{ShortestPath}(u, v) = \min_{p} \text{PathCost}(p) \quad \text{such that} \quad e_0.\text{from\_node} = u \quad \text{and} \quad e_k.\text{to\_node} = v </math>ShortestPath(u,v)=pminPathCost(p)such thate0.from_node=uandek.to_node=v
两个节点间的距离定义为它们之间最短路径的成本:
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> dist ( u , v ) = PathCost ( ShortestPath ( u , v ) ) \text{dist}(u, v) = \text{PathCost}(\text{ShortestPath}(u, v)) </math>dist(u,v)=PathCost(ShortestPath(u,v))
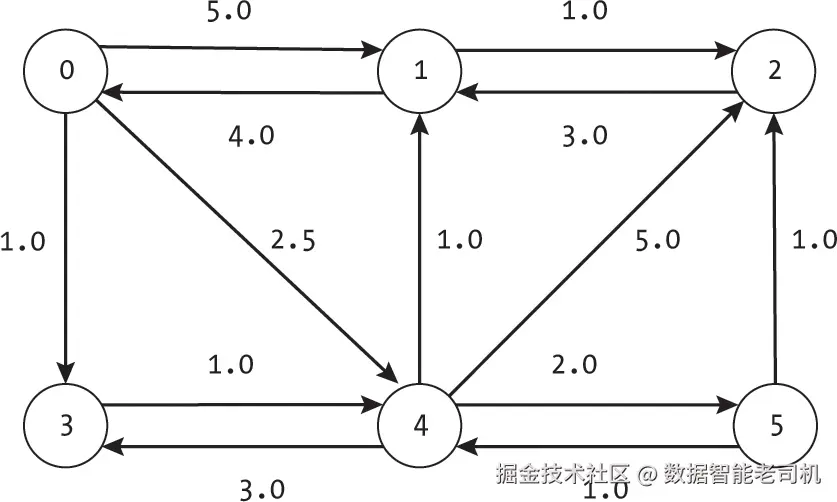
举个具体例子,考虑图7-1中有6个节点的有向图,从节点0到节点5的路径有多种,边上标有权重。我们的目标是找出从节点0到节点5的边序列,使总成本最低。
翻译如下:
表7-1列出了图7-1中从节点0到节点5的几条可能路径的成本,展示了不同路径具有不同的成本。在这个例子中,最短路径是0,3,4,50, 3, 4, 5,其距离为
dist(0,5)=PathCost([0,3,4,5])=4.0\text{dist}(0, 5) = \text{PathCost}([0, 3, 4, 5]) = 4.0。
两个节点之间的最低成本路径不一定是经过最少边数的路径,而可能是经过更多低成本边的路径。
表7-1:从节点0到节点5的路径及其成本
| 路径 | 成本 |
|---|---|
| 0, 3, 4, 5 | 4.0 |
| 0, 4, 5 | 4.5 |
| 0, 1, 0, 3, 4, 5 | 13.0 |
| 0, 3, 4, 3, 4, 5 | 8.0 |
如表7-1所示,路径可以包含环路。如果限制问题只使用正权重边,则环路会严格增加路径成本,因此最短路径算法会避免它们。这一点从现实世界的例子中可以直接看出,比如第4章中冒险者探索迷宫的例子:在迷宫里绕回相同的房间不仅要多走路,还要多次面对重新生成的怪物,增加额外成本。
但是,如果允许负权重边,这个问题变得更加复杂(也不易直观理解)。因此,本章中的算法对负权重使用做了限制,要求路径中不能有负成本的环路。
一个图中两个节点之间可能存在多条最低成本路径。本章的算法只会输出其中一条最低成本路径。
Dijkstra算法
Dijkstra算法由计算机科学家Edsger W. Dijkstra发明,用于找到给定起始节点到图中所有其他节点的最低成本路径。它既适用于无权图,也适用于权重图,但前提是所有边权重均为非负。这个限制反映了现实路径规划问题,我们不能通过多走一步来减少总成本。一个最典型的例子是规划一条公路旅行路线,距离不可能为负,所以不可能通过增加路线长度来缩短旅行距离。
Dijkstra算法的工作原理是维护一组未访问节点,并不断更新每个节点当前估计的最小成本。算法不断减少未访问节点数,每次选择未访问中成本最低的节点访问,然后检查通过该节点到达其未访问邻居节点的路径是否更优。如果更优,则更新邻居节点的成本估计。
由于算法每次都选择当前成本最低的节点访问,因此每访问一个节点时,已经找到了该节点的最短路径。这是因为不允许负权边,路径长度总是递增的。
为了形象说明,考虑算法访问节点vv之前的状态。虽然还没有访问vv的所有邻居,也没有检查所有可能到达vv的路径,但任何一条通向vv的更优路径都必须经过一个未访问节点ww。而由于算法先选择成本最低的节点访问,意味着从起点uu到ww的路径成本至少不小于从uu到vv的路径成本,后续从ww到vv的路径只会增加总成本。
回到第4章中冒险者探索迷宫的例子,Dijkstra算法就像是冒险者逐间房间清理迷宫,详细记录到每个房间的最短路径,方便后续制作地下城指南。冒险者规划下一步时,会考虑能到达哪些未访问的房间,然后确定从起点(迷宫入口)到这些房间的最优路径。路径长度对应从当前房间到相邻房间的花费。
代码示例
下面的代码实现了Dijkstra算法,使用优先队列管理未访问节点:
ini
def Dijkstras(g: Graph, start_index: int) -> list:
cost: list = [math.inf] * g.num_nodes
last: list = [-1] * g.num_nodes
pq: PriorityQueue = PriorityQueue(min_heap=True)
pq.enqueue(start_index, 0.0) # ❶
for i in range(g.num_nodes):
if i != start_index:
pq.enqueue(i, math.inf)
cost[start_index] = 0.0
while not pq.is_empty():
index: int = pq.dequeue() # ❷
for edge in g.nodes[index].get_edge_list():
neighbor: int = edge.to_node
if pq.in_queue(neighbor): # ❸
new_cost: float = cost[index] + edge.weight
if new_cost < cost[neighbor]: # ❹
pq.update_priority(neighbor, new_cost) # ❺
last[neighbor] = index
cost[neighbor] = new_cost
return last这段代码依赖附录B中的优先队列实现,支持动态更新优先级。简单理解,PriorityQueue是支持快速插入带优先级元素、删除优先级最低元素、查询和更新元素优先级的数据结构。
代码先创建辅助数据结构:保存当前最优路径成本的列表cost,保存每个节点上一个节点的列表last,和管理未访问节点的最小堆优先队列pq。起点节点start_index的优先级为0,其余节点初始化为无穷大 ❶。
然后进入循环,依次从优先队列取出成本最低的节点 ❷。对该节点的每条边检查邻居节点是否仍未访问(在队列中) ❸。如果找到通过当前节点到邻居的更优路径,则更新邻居节点的优先级、前驱节点和成本 ❹❺。
当所有节点都被访问后,返回表示路径的前驱节点列表last。
复杂度分析
基于堆的Dijkstra算法中,每个节点被访问一次,节点数为 <math xmlns="http://www.w3.org/1998/Math/MathML"> ∣ V ∣ |V| </math>∣V∣。每次从优先队列取节点和更新优先级的操作时间复杂度为 <math xmlns="http://www.w3.org/1998/Math/MathML"> O ( log ∣ V ∣ ) O(\log |V|) </math>O(log∣V∣)。
遍历所有节点耗时为 <math xmlns="http://www.w3.org/1998/Math/MathML"> ∣ V ∣ log ∣ V ∣ |V| \log |V| </math>∣V∣log∣V∣。
访问每个节点时,遍历其邻居节点的边,边数为 <math xmlns="http://www.w3.org/1998/Math/MathML"> ∣ E ∣ |E| </math>∣E∣,每条边最多更新一次优先级,耗时 <math xmlns="http://www.w3.org/1998/Math/MathML"> O ( log ∣ V ∣ ) O(\log |V|) </math>O(log∣V∣)。
总复杂度为
<math xmlns="http://www.w3.org/1998/Math/MathML"> O ( ( ∣ V ∣ + ∣ E ∣ ) log ∣ V ∣ ) O\big((|V| + |E|) \log |V|\big) </math>O((∣V∣+∣E∣)log∣V∣)
示例说明
图7-2展示了Dijkstra算法在一个5节点图上的执行过程。每个子图显示完成一步后的状态。虚线圆圈表示刚访问的节点,阴影节点表示已访问节点。优先队列pq显示为排序状态(实际存储为堆),方便观察优先级变化。

图7-2(a)表示算法在探索第一个节点之前的状态。冒险者站在入口,准备开始他们的探险。所有节点的last值都是-1,表示我们还不知道如何到达这些节点。节点0的成本是0,因为我们的搜索从这里开始,其他节点的估计成本都是无穷大,因为我们还不知道任何可能的路径。与深度优先搜索和广度优先搜索算法不同,我们从优先队列中加入了所有节点。
在每一步,算法都会探索队列中剩余的最优节点。在图7-2(b)中,算法选择了节点0(唯一一个成本不是无穷大的节点)并访问它。它发现了三个邻居节点:节点1、节点2和节点3。搜索将通过节点0的路径成本与当前成本进行比较。由于新路径的成本都比无穷小,算法更新了这三个节点在last、cost和优先队列pq中的记录。这一更新导致优先队列中节点的顺序发生变化,调整了下一步要探索的节点顺序。
图7-2(c)展示了搜索访问节点2时的情况。节点2只有一个邻居节点3,估计成本为2.0。但是,通过节点2到达节点3的路径现在更优,总成本是0.5 + 1.0 = 1.5。算法将节点3的成本更新为1.5,并将其last更新为2。
对于我们的冒险者来说,房间2为通往房间3提供了一条更好的路径。也许从房间0直接到房间3的路上有一个特别强大的怪物守护。冒险者考虑到未来探险者的需要,重新规划了前往房间3的建议路径,改为通过房间2。
搜索继续进行,图7-2(d)中访问节点3时,发现了通往节点1的更优路径。类似地,图7-2(e)访问节点1时,找到了通往节点4的更好路径。搜索在图7-2(f)访问最后一个节点后完成。
不连通图
如果部分节点从起始节点不可达,会发生什么情况?这有助于我们理解Dijkstra算法在不连通图上的表现。考虑图7-3中的四节点图,从节点0出发时,只有节点0和节点1是可达的。
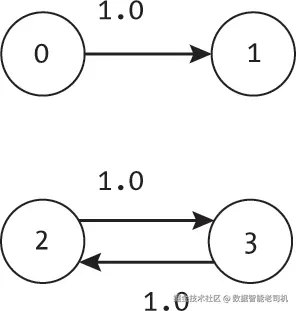
这对应于迷宫中无法到达的房间。根据传说,冒险者知道迷宫有四个房间,但他们只能到达两个。从房间0到房间2或房间3没有路径,因此冒险者只能在笔记中注明这一点。
Dijkstra算法能够轻松处理这种情况。节点2和节点3初始时的last值都是-1,成本为无穷大。因为从节点0无法到达这两个节点,当它们从优先队列中被取出时,成本依然是无穷大。当算法考虑这些节点的邻居时,通过这些节点的估计成本仍然是无穷大,所以算法不会更新它们的cost或last。算法结束时,节点2和节点3的last指针仍是-1。
负权边
在现实问题中,边权可以为负,表示负成本(即收益)。比如在社交网络中的通信,每个好友之间的连接是一条边。每条边的权重代表从一个人传递谣言到另一个人的成本,这个成本可能是发短信或聊天所花费的时间。然而,有时边权可以为负,表示使用该通信渠道的好处。如果两个朋友有一段时间没联系了,重新联络以传递八卦的"成本"可能实际上是负的。
另一种情况是电动车路径规划以最小化电池使用量。如果一条边代表一段陡峭的下坡路,我们可以利用重力和再生制动给电池充电,这段路的电池使用成本就是负的。
需要注意的是,关于负权边,称其为"最短路径"其实不太合理,因为距离不可能为负。无论路径规划多么巧妙,你都不可能安排一次骑行在出发前就回到家。不过,为了与更广泛的文献保持一致,我们仍然用"最短路径"来称呼这些问题。
在考虑带负权边的图的最短路径问题时,我们必须保持一个约束:图中不能包含负环。负环指的是存在一条从某节点回到自身的路径,且这条路径上所有边权之和为负数。在存在负环的情况下,最低成本路径的概念就失去了意义。例如,图7-4中,边(0, 1)的权重是1.0,而边(1, 0)的权重是-2.0。
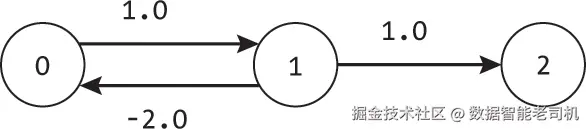
如果我们尝试在图7-4中找到从节点0到节点2的最低成本路径,马上就会遇到问题。如表7-2所示,我们可以不断地增加从节点0到节点1再回到节点0的循环,以进一步降低路径成本。最低成本路径将无限地来回循环下去。
表7-2:图7-4中路径的成本
| 路径 | 成本 |
|---|---|
| 0, 1, 2 | 2 |
| 0, 1, 0, 1, 2 | 1 |
| 0, 1, 0, 1, 0, 1, 2 | 0 |
| 0, 1, 0, 1, 0, 1, 0, 1, 2 | --1 |
| ... | ... |
相比之下,图7-5展示了一个带有负边权但没有负环的图。虽然可以以负成本从节点1到节点0移动,但从节点0回到自身或从节点1回到自身的任何路径的总成本都是正的。
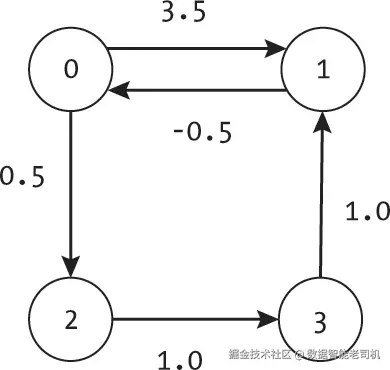
我们如何判断一个图中是否存在负环呢?负环可能非常长,甚至会绕过图中的每一个节点,因此并不容易被立即发现。Bellman-Ford算法通过检测图中是否存在负环来解决了这个问题。
Bellman-Ford算法
Dijkstra算法的一个主要缺点是它只适用于边权为正的图。而Bellman-Ford算法则打破了这一限制,但代价是增加了计算开销。
Bellman-Ford算法的工作方式是反复遍历边的列表,利用边的信息来更新到每个节点的最优成本(这一过程称为松弛)。与Dijkstra算法类似,它维护一个名为cost的列表,存储从起点到每个节点的当前最佳成本估计。每次Bellman-Ford处理一条边时,它会检查是否通过这条边可以找到一条更优路径到该边的终点节点,这通过比较该节点当前的成本估计(cost中的值)与通过这条边的起点节点(加上边权重)到达该终点节点的成本来实现。算法不断重复此过程,逐步优化路径的估计。
我们可以把这个算法想象成一个极为细致的旅行代理,正在为即将到来的旅行季规划最便宜的航班。代理从一个起点城市(比如芝加哥)开始,寻找到世界各地目的地的最低成本路径。显然,代理本人不可能亲自乘坐所有航班(即不可能走遍整个图),但他们可以快速浏览航班列表和价格,更新自己的路径估计表。
经过一次完整浏览航班列表后,代理就知道了从芝加哥出发到每个城市的最佳直达航班。接着代理再一次浏览航班列表,询问是否可以利用已有的最佳路径构建出更优的组合路径。他们反复扫描列表,更新估计值,直到找到到每个目的地的最佳路径。
就像这位旅行代理一样,Bellman-Ford算法的每一次外层循环迭代,都是在逐步构建更优的路径。图7-6展示了这一过程,其中粗线表示每次迭代后,从节点2到节点0的已知最佳路径。
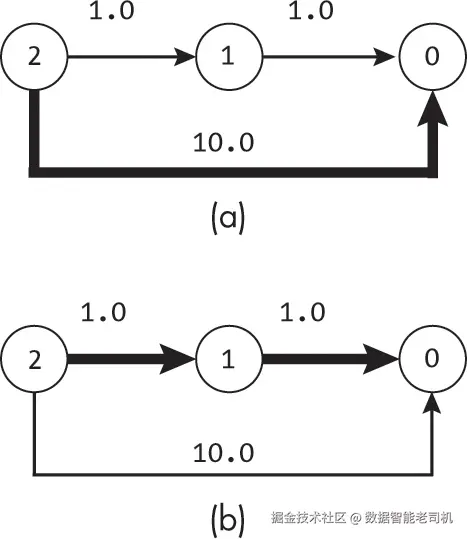
图7-6(a)展示了经过对每条边进行一次迭代后,从节点2到节点0的最佳路径。由于算法只看过每条边一次,它只发现了从节点2直接到节点0的路径,路径成本为10.0。算法还没有机会意识到可以利用边(2, 1)和(1, 0)构建一条更优的路径。在第二次迭代中,算法利用了从节点2到节点1成本为1.0的路径,进而构建了一条到节点0的路径。到节点0的最佳路径被更新为经过节点1,成本为2.0,如图7-6(b)所示。
我们可以将总迭代次数限制为|V| -- 1,其中|V|是图中节点的数量。由于不允许存在负环,最低成本路径绝不会回到同一个节点,因为这样做会严格增加路径成本。这也解释了现实世界中不同城市之间的旅行行程不会包含环路------即不会多次中转同一个机场。
因为最低成本路径不会重复访问节点,它最多只能经过所有|V|个节点,并使用|V| -- 1条边。例如,在图7-7的六节点图中,从节点0到节点1的最低成本路径是[0, 3, 4, 5, 2, 1]。尽管存在步数更少的备选路径,但从节点0到节点1的最低成本路径使用了五条边,且访问了图中的所有节点。
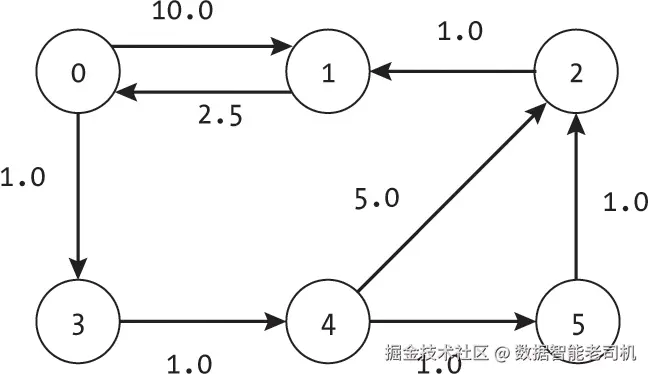
Bellman-Ford算法利用这个约束既用来停止算法,也用来检测负环。经过|V| -- 1次外层循环后,它已经找到了所有可能的最低成本路径。由于该算法使用了两个嵌套的for循环(一个遍历节点数,一个遍历每条边),其时间复杂度为|E| × |V|。
除非存在负环,否则多余的遍历不会带来帮助。算法利用这一点,进行一次额外的遍历,检测是否还有路径成本降低。如果发现成本仍在下降,则说明图中存在负环。
我们可以把这个检测过程想象成旅行代理做的最后一次核查。他们发现,在匹兹堡和波士顿之间再加一段航程竟然能进一步降低价格。感到困惑的代理查看航班数据,发现芝加哥到波士顿,再到匹兹堡,再回到波士顿,最后到西雅图的路线是目前最便宜的选择。波士顿到匹兹堡再回波士顿的循环构成了一个负环。显然航班定价出现了问题,形成了一个实际上"负收费"的循环。旅行代理赶紧联系客户,提醒在航空公司修正问题前,有可能免费来一次10站的旅行。
代码示例:
Bellman-Ford算法对所有边进行|V| -- 1次迭代。每次迭代都会问一个简单的问题:"当前这条边能否提供到其目标节点更优的路径?"以下代码使用两个for循环来完成该搜索:
ini
def BellmanFord(g: Graph, start_index: int) -> Union[list, None]:
cost: list = [math.inf] * g.num_nodes
last: list = [-1] * g.num_nodes
all_edges: list = g.make_edge_list()
cost[start_index] = 0.0
for itr in range(g.num_nodes - 1):
for edge in all_edges:
❶ cost_thr_node: float = cost[edge.from_node] + edge.weight
❷ if cost_thr_node < cost[edge.to_node]:
cost[edge.to_node] = cost_thr_node
last[edge.to_node] = edge.from_node
for edge in all_edges:
❸ if cost[edge.to_node] > cost[edge.from_node] + edge.weight:
return None
return lastBellmanFord()函数接收一个图和起始节点索引,返回到每个节点的最佳路径(通过last数组表示),如果图中存在负环则返回None。这里需要从Python的typing库导入Union以支持多类型返回值的类型提示。
代码开始时创建了辅助数据结构,包括当前到各节点的最佳成本(cost)和路径上前一个节点(last)。它还通过make_edge_list()函数提取了图中所有边的列表,该函数遍历每个节点并收集图中所有边。最后将起始节点的成本设为0.0。
两个嵌套的for循环驱动着对所有边进行|V| -- 1次迭代。对每条边,代码计算通过该边到达目标节点的成本 ❶。如果这个成本低于当前已知的最佳成本 ❷,则更新目标节点的成本和路径。需要注意的是,成本的降低不一定意味着路径上的前驱节点发生改变,也可能是前驱节点的成本因为更优路径被更新了。
完成|V| -- 1次迭代后,算法完成了路径优化。在结束前,算法会检查解是否有效。如果还有任意一条边可以使成本降低 ❸,则说明图中存在负环,算法返回None;否则返回last数组。
案例说明:
图7-8展示了Bellman-Ford算法外层循环的第一次迭代。由于算法总共需要进行 (|V| -- 1) × |E| 次步骤(|E|为边数),全部36步不便展示。这里仅展示第一轮外层循环中路径(last数组)和估算成本的变化情况。每个子图表示检查加粗边后的算法状态。
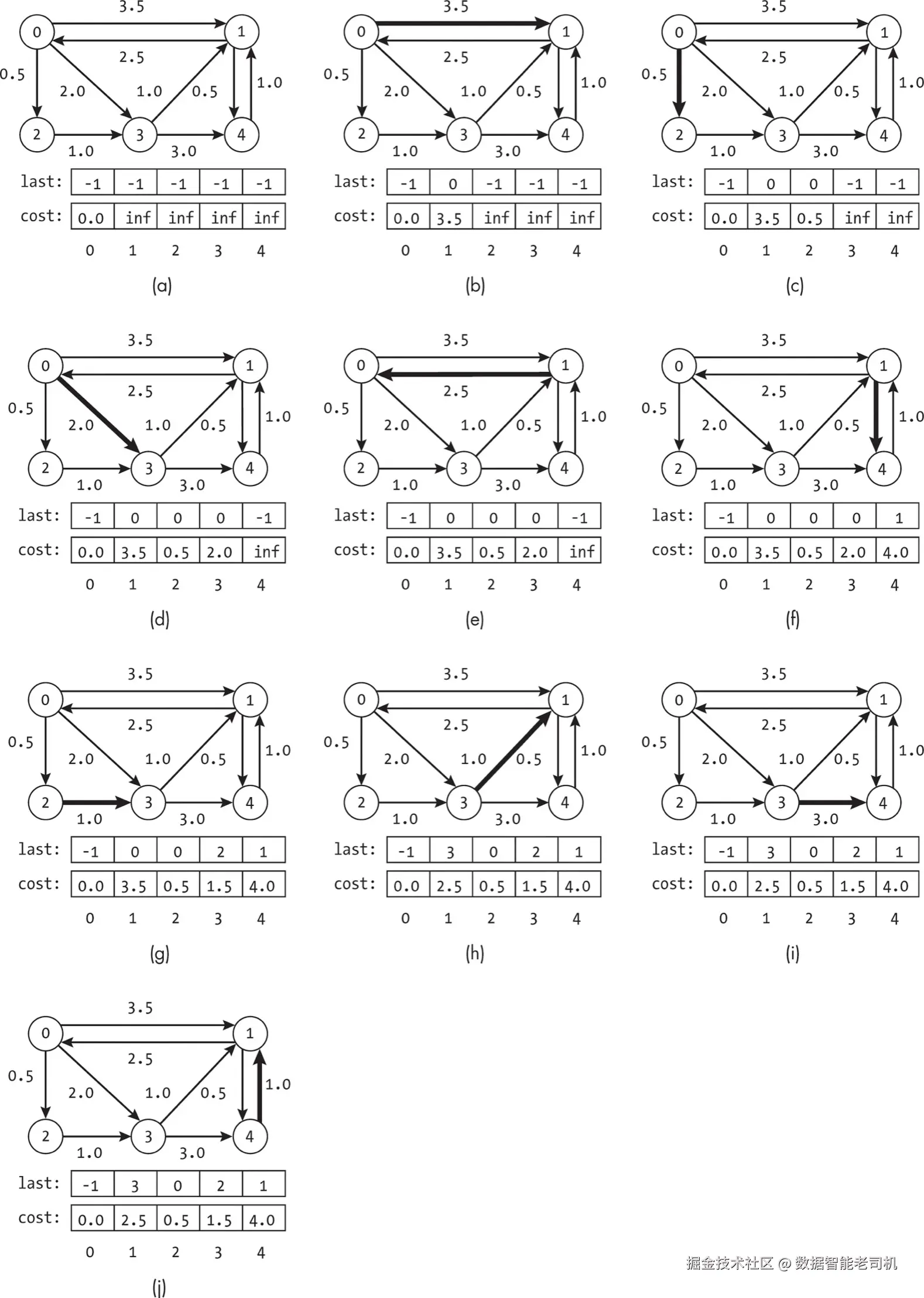
图7-8(a)展示了算法在检查任何边之前的状态。除了起始节点外,所有节点的估计成本都是无穷大。在图7-8(b)中,算法测试了第一条边,发现它能为目标节点1提供更优路径,于是将节点1的路径更新为从节点0出发,最佳成本更新为3.5。
搜索继续遍历图中的每条边,每次迭代都考虑当前边的目标节点的成本。在图7-8(c)中,算法找到了到节点2的更优路径;在图7-8(d)中,找到了到节点3的更优路径。图7-8(e)中没有更新,因为从节点0到节点0的最佳成本是0.0,且不需要通过节点1做无谓的环路回到起点。
在外层循环第一次迭代结束时,如图7-8(j)所示,搜索已经检查了每条边并更新了最佳路径和成本估计。然而算法尚未完成。到节点4的真正最佳路径是[0, 2, 3, 1, 4],成本为3.0。只有在重新考虑边(1, 4)时,算法才会找到这个最终成本。因为在第一轮考虑这条边时,节点1的最佳路径尚未确定,其成本估计仍然偏大。
随着算法的继续,它不断地重新访问边并持续更新最佳路径及其成本。图7-9展示了算法的最终步骤。
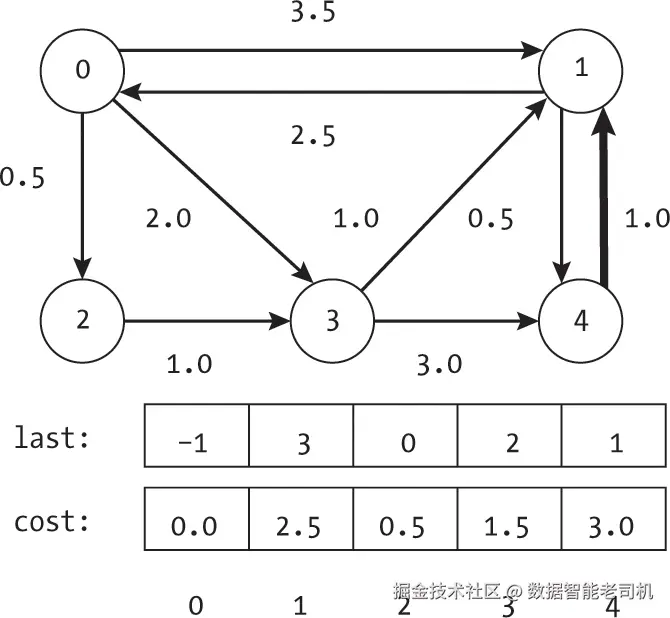
在第四次检查边 (4, 1) 之后,算法完成了两层循环。此时,成本和路径已经收敛到它们的真实值。
所有节点对最短路径问题
无论是我们的探险者,还是旅行代理人的例子,都满足于找到从给定起点节点到图中所有其他节点的最低成本路径。然而,如果我们想找到图中任意两个节点之间的最短路径怎么办?即使在前面两个类比的情境下,也能体会到这种需求的吸引力。探险者绘制完整个魔法迷宫的地图后,可能希望在任意房间之间来回移动,以帮助遇险的其他探险者。类似地,旅行代理人可能希望进行全球规划,安排从任何出发地到世界任何目的地的行程。在这两种情况下,我们都需要找到任意两节点间的最低成本路径。
所有节点对最短路径问题旨在求出图中每一对节点之间的最短路径。换句话说,我们希望构建一个矩阵 last,使得每一行 last[i] 包含从节点 i 出发路径上的前驱节点列表。在这种表示中,矩阵中的元素 last[i][j] 表示从 i 到 j 的路径中,节点 j 前面的那个节点。就像前面各种搜索算法和最短路径算法中使用的 last 数组一样,给定固定起点,我们可以从目标节点开始,沿着前驱节点一路回溯到起点。
我们可以通过在本章讨论的任一算法外层再加一个循环,解决所有节点对最短路径问题。例如,可以用单层循环配合 Bellman-Ford 算法填充 last 矩阵:
sql
last: list = []
for n in range(g.num_nodes):
last.append(BellmanFord(g, n))
return last由于 Bellman-Ford 算法的时间复杂度是 |E|×|V|,因此这种做法的总复杂度是 |E|×|V|²。类似地,我们也可以用 Dijkstra 算法(本章实现的版本)进行多次调用,其复杂度为 |V| × (|V| + |E|) × log(|V|)。这相当于在每个城市打电话给旅行代理,询问从该城市出发的最低成本行程。借助每个起点到所有可能目的地的最短路径信息,我们可以组装出任意两城市间的旅行成本。
下一节介绍一种寻找所有最短路径的替代算法:Floyd-Warshall 算法。该算法非常适合于边数 |E| 远大于节点数 |V| 的稠密图。它不再迭代未访问节点或所有边,而是考虑每个可能出现在路径中间的节点,并决定是否将其包含。
Floyd-Warshall 算法
Floyd-Warshall 算法通过迭代地考虑并优化每对起点和终点之间的中间节点来解决所有节点对最短路径问题。所谓中间路径,是指起点之后、终点之前经过的节点。算法通过不断考虑将节点加入中间路径,逐步构建更优路径。外层循环遍历每个节点 u,询问:"如果路径中包含停靠点 u,是否会得到更优路径?"对每个中间节点 u,算法检测所有待考虑路径,看是否会有帮助,如果有,则更新路径。
过程中,我们维护了 last 和 cost 矩阵,它们是之前 Dijkstra 和 Bellman-Ford 中使用的数组的矩阵版本。矩阵的每一行对应单一起点的数组,每个元素表示特定终点的值(成本或路径上的前驱节点)。初始化时,cost[u][v] 若存在边 (u, v) 则为该边权重,若 u = v 则为0,否则为无穷大。类似地,last[u][v] 若存在边 (u, v) 且 u ≠ v,则为 u,否则为 -1 表示路径不存在。
图7-10展示了 Floyd-Warshall 算法的一个示例状态。左侧的图用于参考,右侧两个矩阵显示当前估计的成本和最佳路径。这一初始状态相当于旅行代理仅规划客户直达航班的情况。只有当存在从 u 到 v 的直飞航班时,城市对 (u, v) 才被考虑。其他城市间的成本视为无穷大。

Floyd-Warshall 算法利用一种称为动态规划的计算技术,有效地通过包含中间节点集合 {0, 1, ..., k} 的路径,基于仅包含中间节点集合 {0, 1, ..., k -- 1} 的路径,逐步构建最优路径。由于不允许负环路,每个节点在路径中最多只能使用一次。对于每一对起点和终点 (u, v),算法检查是否存在一条通过节点 k 的更优路径,该路径仅使用中间节点集合 {0, 1, ..., k}。我们可以通过复用前一次迭代(k -- 1)的 cost 和 last 矩阵来实现这一点。如果存在通过 k 的更优路径,那么从 u 到 k 的最佳路径成本与从 k 到 v 的最佳路径成本之和,必须小于当前从 u 到 v 的路径成本。我们可以直接从上一次迭代的 cost 和 last 矩阵中读取这些路径及其成本。
为了理解其工作原理,来看图7-11中的图和算法状态,该状态发生在图中潜在中间节点为 0、1 和 2 的路径已被测试之后。此时,cost 和 last 矩阵表示允许中间节点属于集合 {0, 1, 2} 的最佳路径。从节点 0 到节点 1 的最佳路径仍然是直接路径 [0, 1],因为此时尚不能使用节点 3。
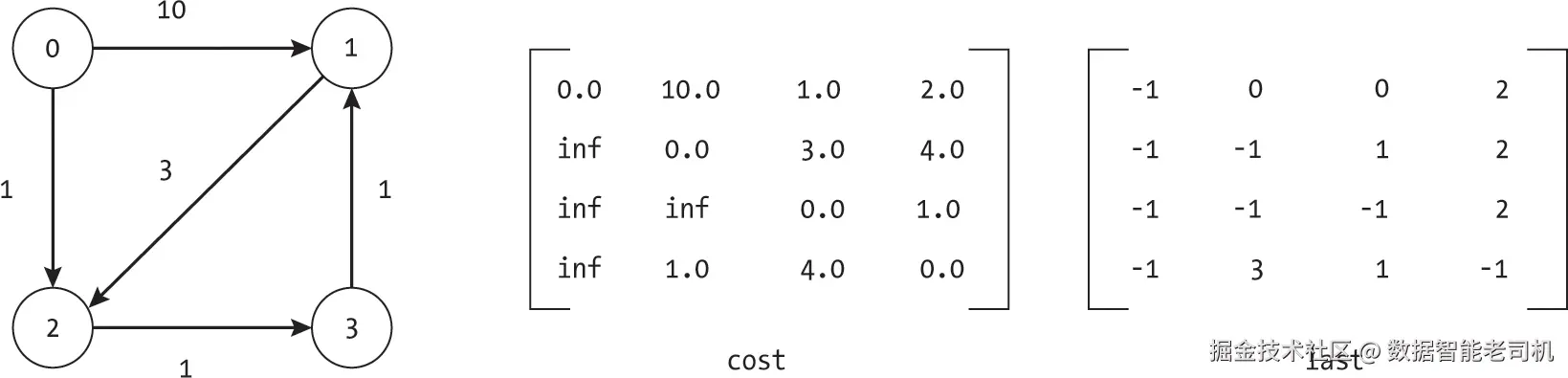
当我们考虑可以使用节点 3 作为中间节点的路径时,发现了几条更优路径,如图 7-12 所示。我们再次来看从节点 0 到节点 1 的路径。当我们询问是否存在一条通过节点 3 的更优路径时,发现确实存在。通过节点 3 的路径总成本为 3.0,因为从节点 0 到节点 3(经过节点 2)的路径成本是 2.0,而从节点 3 到节点 1 的路径成本是 1.0。
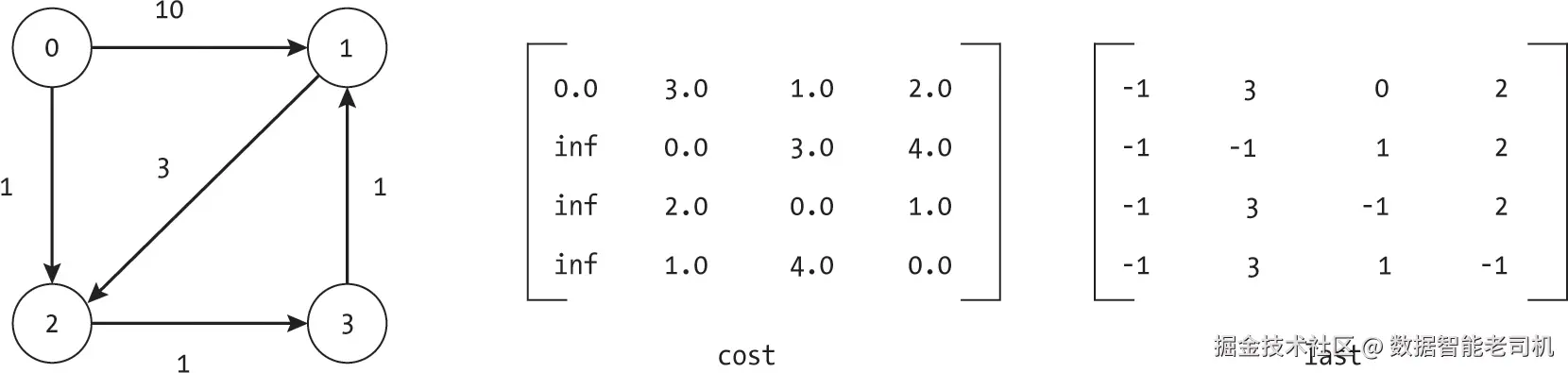
通过将节点 3 作为从节点 0 到节点 1 路径中的中间节点,我们也将节点 2 包含进来了。此时的最优路径变为 [0, 2, 3, 1]。这展示了 Floyd-Warshall 迭代方法的强大之处:我们不仅仅孤立地考虑中间节点,还考虑了通往该节点和从该节点出发的最优路径。
由于算法需要对每对节点之间的路径,针对所有可能的中间节点进行改进测试,因此需要三重嵌套循环遍历所有节点。算法的时间复杂度因此是 |V|³。虽然看起来计算成本较高,但之前的方法的运行时间也依赖于边数和节点数的相对关系。
代码
Floyd-Warshall 算法的核心是三重嵌套的 for 循环,先遍历要加入的中间节点 k,再遍历需要路径的每一对节点 (i, j),代码如下:
ini
def FloydWarshall(g: Graph) -> list:
N: int = g.num_nodes
cost: list = [[math.inf] * N for _ in range(N)]
last: list = [[-1] * N for _ in range(N)]
❶ for i in range(N):
for j in range(N):
if i == j:
cost[i][j] = 0.0
else:
edge: Union[Edge, None] = g.get_edge(i, j)
if edge is not None:
cost[i][j] = edge.weight
❷ last[i][j] = i
for k in range(N):
for i in range(N):
for j in range(N):
❸ if cost[i][j] > cost[i][k] + cost[k][j]:
cost[i][j] = cost[i][k] + cost[k][j]
❹ last[i][j] = last[k][j]
return last代码首先初始化 cost 和 last 矩阵。使用一对嵌套循环遍历每个元素 ❶。对角线元素(i == j)的最优代价设为 0.0,两个节点间有边连接时设为边权重,否则为无穷大。代码通过调用 Graph 类的 get_edge() 函数来检查并获取边,因此需要额外导入 Python 的 typing 库中的 Union。同样,任何有边连接的节点对,其 last 矩阵的值设为起点 i,其他(包括对角线)设为 -1 ❷。
主要计算过程在三重嵌套循环中进行。外层循环遍历当前考虑的中间节点 k,内层两个循环遍历节点对 (i, j)。代码判断是否能通过中间节点 k 找到更优路径 ❸,若能,则更新 cost 和 last 矩阵 ❹。与书中之前的算法不同,last[i][j] 更新为路径中从 k 到 j 的最后一步节点。
当算法检查完所有可能的中间节点和所有起点-终点对后,返回最终的 last 矩阵。
示例
图 7-13 展示了 Floyd-Warshall 算法在一个五节点图上的运行示例。前五个子图分别展示了加入对应虚线节点作为可能中间节点后,数据结构的状态。阴影节点表示已被加入。图 7-13(a) 显示第一次迭代前的状态,图 7-13(b) 显示第一次迭代结束后,节点 0 被作为中间节点考虑后的状态。
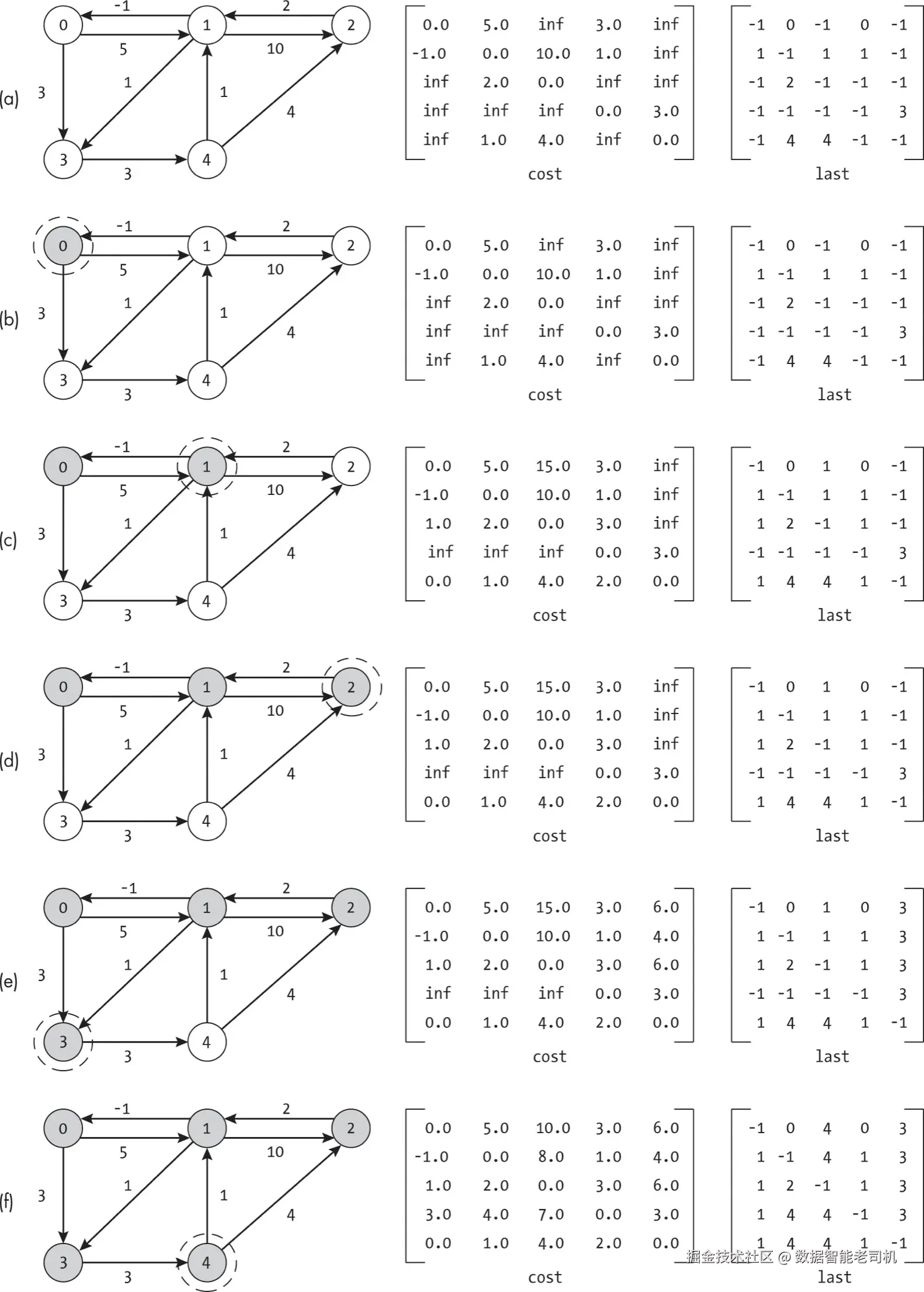
考虑这个例子,放在我们旅行代理征服全球市场的背景下。他们建立了两张电子表格,第一张(cost)记录起点和终点的城市对及其总费用,第二张(last)记录同样的城市对以及行程中终点前面紧挨着的城市。由于不知从何开始,代理先填写了直达航班,如图 7-13(a) 所示。cost 矩阵包含任意两城市间航班的费用(飞往同一城市为 0.0),如果没有直达航班则为无穷大。last 矩阵记录航班起点城市,若无前一个城市则为 -1。这就是算法的初始状态。
接下来,旅行代理考虑芝加哥(节点 0),问自己:"如果我让客户经停这个城市会怎样?当然,我会用目前已知的从起点到芝加哥的最佳路径,再加上从芝加哥到目的地的最佳路径。这里只添加一个中转城市。"如图 7-13(b) 所示,这并没有改善任何路径,代理的矩阵没有变化。
代理接着考虑纽约(节点 1),同样提问。如图 7-13(c),可能性增加了。通过在纽约中转,芝加哥(节点 0)出发的旅客现在可以到达缅因州波特兰(节点 2)。同样,从波特兰(节点 2)和夏洛特(节点 4)出发的旅客,可以到达芝加哥(节点 0)和匹兹堡(节点 3)。
代理的成功激励他们立刻考虑在波特兰(节点 2)中转。但这没有带来多少帮助,因为以波特兰作为中转并未降低任何路径的费用。代理叹息,怀疑纽约的成功是偶然的,但仍继续搜索。
经过考虑匹兹堡(节点 3)后,代理的坚持得到了回报,图 7-13(e) 的矩阵显示,代理发现了从芝加哥(节点 0)、纽约(节点 1)和波特兰(节点 2)出发到夏洛特(节点 4)的新路径。
不过,到目前为止,代理只找到了通往新城市的路径,没有任何中转降低了已有路径的费用。因此,考虑夏洛特(节点 4)成为一个重要转折点,因为它为多条旅行线路提供了更优中转。此前,从芝加哥到波特兰的路径是 [0, 1, 2],费用为 15。现在旅客可以走 [0, 3, 4, 2],费用仅为 10。甚至从纽约到波特兰的路线,通过 [1, 3, 4, 2] 中转,也比直飞更便宜。
计算图的直径
图的直径是衡量图中节点最大距离的指标。定义为图中任意两节点之间最短路径代价的最大值:
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> diameter = max u ∈ E , v ∈ E dist ( u , v ) \text{diameter} = \max_{u \in E, v \in E} \text{dist}(u, v) </math>diameter=u∈E,v∈Emaxdist(u,v)
其中,dist(u, v) 是 u 到 v 的最短路径代价。本章中的算法可以用来计算这一指标,以便分析或比较不同图结构。
举例来说,我们的迷宫探险者经过多年征战,征服了上百个地下迷宫和无数怪物,决定退休并开设迷宫援助服务。他们希望选一个迷宫长期驻守,帮助其他探险者(收费合理)。关键是能多快赶到遇险客户身边,因为如果怪物先到,援助就无意义(客户也付不了钱)。复杂的是,援助者和客户可能同时在迷宫中的任意节点,如果有多个客户,援助者还得在房间间奔波。
探险者决定选择直径介于 5 到 10 个房间的迷宫。直径太大赶不及援助,太小又没挑战意义。确认后,他们计算附近所有迷宫的直径,选择合适的一个。
我们可以直接从 Floyd-Warshall 算法中的 cost 矩阵里找出最大值,或通过 last 矩阵反向遍历每条路径计算总成本。下面是第二种方法的示例代码,演示如何用 last 矩阵:
ini
def GraphDiameter(g: Graph) -> float:
❶ last: list = FloydWarshall(g)
max_cost: float = -math.inf
for i in range(g.num_nodes):
for j in range(g.num_nodes):
cost: float = 0.0
current: int = j
❷ while current != i:
prev: int = last[i][current]
❸ if prev == -1:
return math.inf
edge: Union[Edge, None] = g.get_edge(prev, current)
cost = cost + edge.weight
current = prev
❹ if cost > max_cost:
max_cost = cost
return max_cost这段代码先用 Floyd-Warshall 算法计算出路径矩阵 last ❶。然后对所有起点和终点配对 (i, j) 进行双重循环。对每对节点,从终点开始反向遍历 last 矩阵,直到回到起点 ❷。遍历过程中取出每条边并累加权重。如果途中遇到死路(即 last[i][current] == -1 但 current 不等于 i),说明两点间无路径,函数返回无穷大 ❸。遍历完所有配对后,返回路径成本最大值,即图的直径 ❹。
这为什么重要
最低成本算法直接应用于许多现实世界的问题中,从路径规划到优化都有广泛用途。本章介绍的算法提供了高效寻找此类路径的实用方法。无论是 Dijkstra 算法还是 Bellman-Ford 算法,都能返回图中所有可能终点的最优解。Floyd-Warshall 算法则更进一步,能返回所有可能起点和终点之间的最短路径。
本章介绍的三种算法还展示了可适用于解决其他图论问题的通用技巧。Dijkstra 算法维护一个优先队列,存放未访问的节点,这些节点代表了探索的前沿。在第10章,我们将看到另一种算法也采用了类似的方法来解决不同的优化问题。Bellman-Ford 算法则展示了基于边集合操作的算法思路。Floyd-Warshall 算法体现了一种更复杂的动态规划方法------它通过从较小的中间节点子集构造最优路径,逐步扩展到包含更多中间节点的路径。
下一章将介绍一些算法,这些算法可以利用额外的启发式信息,减少寻找给定起点到终点的最低成本路径时需要访问的节点数量。虽然这些算法不能找到比本章算法更短的路径,但通过聚焦于最有希望的节点,它们能实现更快的运行速度。