《信息学奥赛一本通》第52题:求一元二次方程
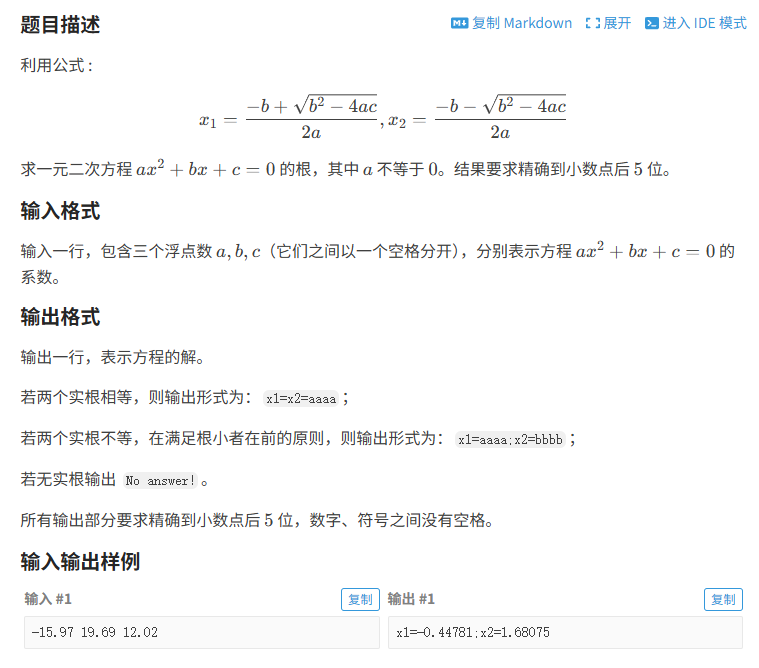
题目描述
利用公式 :
x 1 = − b + b 2 − 4 a c 2 a , x 2 = − b − b 2 − 4 a c 2 a x_1=\frac{-b+\sqrt{b^2-4ac}}{2a} , x_2=\frac{-b-\sqrt{b^2-4ac}}{2a} x1=2a−b+b2−4ac ,x2=2a−b−b2−4ac求一元二次方程 a x 2 + b x + c = 0 ax^2+bx+c=0 ax2+bx+c=0 的根,其中 a a a 不等于 0 0 0。结果要求精确到小数点后 5 5 5 位。
输入格式
输入一行,包含三个浮点数 a , b , c a,b,c a,b,c(它们之间以一个空格分开),分别表示方程 a x 2 + b x + c = 0 ax^2+bx+c=0 ax2+bx+c=0 的系数。
输出格式
输出一行,表示方程的解。
若两个实根相等,则输出形式为:
x1=x2=aaaa;若两个实根不等,在满足根小者在前的原则,则输出形式为:
x1=aaaa;x2=bbbb;若无实根输出
No answer!。所有输出部分要求精确到小数点后 5 5 5 位,数字、符号之间没有空格。
输入输出样例 #1
输入 #1
-15.97 19.69 12.02
输出 #1
x1=-0.44781;x2=1.68075
大家好,我是莫小特。
这篇文章给大家带来《信息学奥赛一本通》中的第 52 题:求一元二次方程。

一、题目描述
洛谷的题号是:B2053 求一元二次方程
二、题意分析
这道题是信息学奥赛一本通练习题的第 52 题。
输入一行,包括三个浮点数 a、b、c,数据范围未说明,因此先试用 double 类型。
cpp
double a,b,c;
cin>>a>>b>>c;输入完成后,我们来分析题意,根据题目意思,要根据输入的三个浮点数来求一元二次防尘袋根,结果要精确到小数点后 5 位,题目中也给定了具体的计算公式,因此只需要将计算公式转换为程序语言即可。
考虑到都是小数,因此两个根也定义为 double 类型。
公式中有 b 2 − 4 a c \sqrt{b^2-4ac} b2−4ac ,需要用到 #include<camth> 头文件中的 sqrt() 函数。
cpp
double x1=(-b+sqrt(b*b-4*a*c))/(2*a);
double x2=(-b-sqrt(b*b-4*a*c))/(2*a); 但这样不能直接输出,要根据输出格式的要求输出,即如果两个实根相等,要按样式输出 x1=x2=aaaa,如果没有实根,则输出 No answer!,所以不能简单的判断 x1 和 x2 的值,应该先判断是否有实根,根据一元二次方程的特点,想要判断是否存在实根,需要 ∆ 的值,也就是 b 2 − 4 a c b^2-4ac b2−4ac 的值,所以定义一个新的 double 变量存储 ∆ 的值。
cpp
double detal=b*b-4*a*c;如果 detal 变量的值小于 0,证明没有实根,输出 No answer!。
cpp
if(detal<0)
{
cout<<"No answer!";
}如果 detal 变量等于 0,证明两个实根相等,需要按要求的格式输出,并要精确到小数点后 5 位,精确到小数点后 5 位,使用 printf(%.5lf) 实现。
cpp
else
{
if(x1==x2)
{
printf("x1=x2=%.5lf",x1);
}
}剩下的只需要对 x1 和 x2 的值进行判断即可,如果 x1 大于 x2,则 x2 的值在前,如果 x1 小于 x2,则 x1 的值在前。
cpp
else if(x1>x2)
{
printf("x1=%.5lf;x2=%.5lf",x2,x1);
}
else
{
printf("x1=%.5lf;x2=%.5lf",x1,x2);
}按照样例输入对数据进行验证。

符合样例输出,到网站提交测评。
测试通过!
三、完整代码
该题的完整代码如下:
cpp
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
int main()
{
double a,b,c;
cin>>a>>b>>c;
double x1=(-b+sqrt(b*b-4*a*c))/(2*a);
double x2=(-b-sqrt(b*b-4*a*c))/(2*a);
double detal=b*b-4*a*c;
if(detal<0)
{
cout<<"No answer!";
}
else
{
if(x1==x2)
{
printf("x1=x2=%.5lf",x1);
}
else if(x1>x2)
{
printf("x1=%.5lf;x2=%.5lf",x2,x1);
}
else
{
printf("x1=%.5lf;x2=%.5lf",x1,x2);
}
}
return 0;
}四、总结
本题是经典的公式转换,考察了以下知识点:
1、数学公式应用:熟练使用一元二次方程根公式
x 1 , 2 = − b ± b 2 − 4 a c 2 a x_{1,2}=\frac{-b\pm \sqrt{b^2-4ac}}{2a} x1,2=2a−b±b2−4ac
在使用时要保证变量都在 double 类型内,避免出现精度错误。
2、判别式计算,即 ∆ 的值。
Δ > 0 \Delta > 0 Δ>0 → 两个不等实根
Δ = 0 \Delta = 0 Δ=0 → 两个相等实根
Δ < 0 \Delta < 0 Δ<0 → 无实根
也就是以下公式:
cpp
double delta = b*b - 4*a*c;---end---
如果你觉得这篇文章对你有帮助,欢迎点赞、收藏、关注我哦!
如果有更好的方法也可以在评论区评论哦,我都会看哒~
我们下集见~