【大语言模型 17】高效Transformer架构革命:Reformer、Linformer、Performer性能突破解析
关键词:Transformer变种、Reformer、Linformer、Performer、注意力机制优化、长序列处理、计算复杂度、LSH注意力、线性注意力、Kernel方法、内存优化、序列建模
摘要:本文深度解析三种突破性的Transformer变种架构:Reformer、Linformer和Performer。通过费曼学习法,从计算复杂度问题出发,详细解释每种架构的核心创新点、实现原理和适用场景。重点讲解LSH注意力、线性复杂度近似和Kernel方法在注意力机制中的应用,帮助读者理解如何突破传统Transformer的计算瓶颈,实现高效的长序列处理。
文章目录
- [【大语言模型 17】高效Transformer架构革命:Reformer、Linformer、Performer性能突破解析](#【大语言模型 17】高效Transformer架构革命:Reformer、Linformer、Performer性能突破解析)
-
- 引言:传统Transformer的困境与变革需求
- 第一部分:传统Transformer的复杂度瓶颈
- [第二部分:Reformer - 局部敏感哈希的智慧](#第二部分:Reformer - 局部敏感哈希的智慧)
- [第三部分:Linformer - 线性复杂度的优雅解决方案](#第三部分:Linformer - 线性复杂度的优雅解决方案)
- [第四部分:Performer - Kernel方法的创新应用](#第四部分:Performer - Kernel方法的创新应用)
- 第五部分:三种方法的深度对比与选择指南
- 第六部分:实际应用案例与最佳实践
- 第七部分:未来发展趋势与思考
- 总结:架构选择的智慧
引言:传统Transformer的困境与变革需求
想象一下,你正在阅读一本10万字的小说,需要理解每个词与其他所有词之间的关系。传统的Transformer模型就像一个需要同时记住所有词汇关系的超级大脑,但随着文本长度的增加,这个"大脑"的负担呈平方级增长。
这就是传统Transformer面临的核心问题:二次复杂度困境。当序列长度翻倍时,计算量和内存需求会增加4倍!这使得处理长文档、长对话或长序列数据变得极其困难。
今天,我们将探索三种革命性的解决方案:Reformer、Linformer和Performer。它们就像三位不同的建筑师,各自用独特的方法重新设计了注意力机制这座"大厦"。
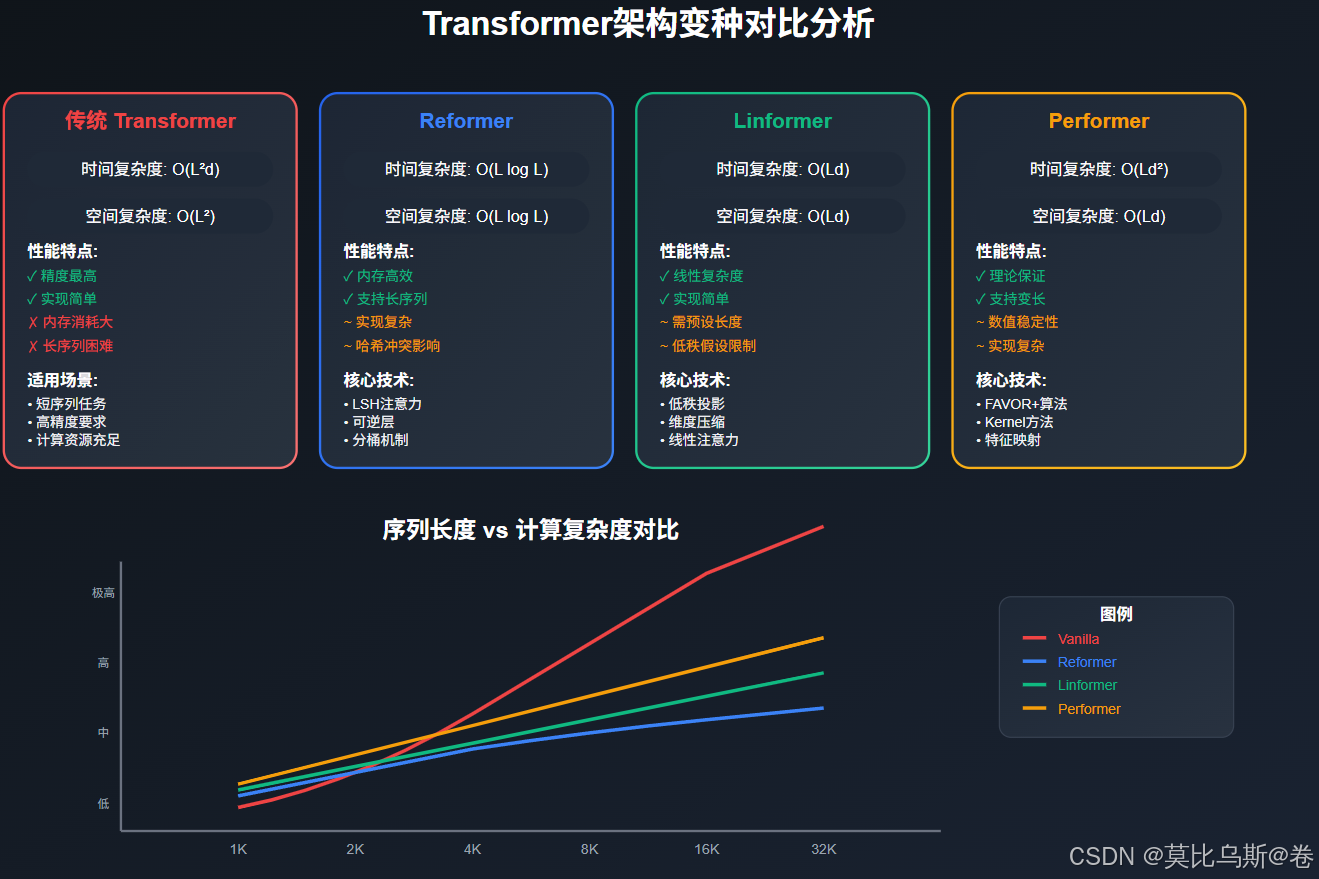
第一部分:传统Transformer的复杂度瓶颈
为什么传统Transformer会遇到瓶颈?
让我们先理解问题的根源。在传统的Self-Attention机制中:
python
# 传统Self-Attention的计算过程
def vanilla_attention(Q, K, V, seq_len, d_model):
"""
传统注意力机制
Q, K, V: [batch_size, seq_len, d_model]
"""
# 1. 计算注意力分数矩阵
attention_scores = torch.matmul(Q, K.transpose(-2, -1)) # [batch, seq_len, seq_len]
# 2. 缩放
attention_scores = attention_scores / math.sqrt(d_model)
# 3. Softmax归一化
attention_weights = F.softmax(attention_scores, dim=-1)
# 4. 计算输出
output = torch.matmul(attention_weights, V) # [batch, seq_len, d_model]
return output
# 复杂度分析
# 时间复杂度: O(seq_len²)
# 空间复杂度: O(seq_len²) - 需要存储注意力矩阵具体的复杂度问题
让我们用具体数字来理解这个问题:
python
def analyze_complexity(seq_len, d_model=512):
"""分析不同序列长度下的计算复杂度"""
# 注意力矩阵大小
attention_matrix_size = seq_len * seq_len
# 内存需求(假设float32,4字节)
memory_gb = (attention_matrix_size * 4) / (1024**3)
# 计算量(FLOPs)
flops = seq_len * seq_len * d_model
print(f"序列长度: {seq_len}")
print(f"注意力矩阵大小: {attention_matrix_size:,}")
print(f"内存需求: {memory_gb:.2f} GB")
print(f"计算量: {flops:,} FLOPs")
print("-" * 40)
# 不同序列长度的复杂度对比
for length in [512, 1024, 2048, 4096, 8192]:
analyze_complexity(length)输出结果会显示,当序列长度从512增加到8192时,内存需求从1MB增长到256MB,计算量增长了256倍!
第二部分:Reformer - 局部敏感哈希的智慧
Reformer的核心思想
Reformer就像一个聪明的图书管理员,不需要检查图书馆中的每一本书,而是使用一套巧妙的索引系统来快速找到相关的书籍。
Reformer的两大核心创新:
- LSH注意力(Locality-Sensitive Hashing Attention):将相似的查询和键分组
- 可逆层(Reversible Layers):减少内存消耗
LSH注意力机制详解
python
import torch
import torch.nn as nn
import numpy as np
class LSHAttention(nn.Module):
def __init__(self, d_model, n_hashes=8, bucket_size=64):
super().__init__()
self.d_model = d_model
self.n_hashes = n_hashes
self.bucket_size = bucket_size
# 随机投影矩阵
self.hash_weights = nn.Parameter(
torch.randn(n_hashes, d_model // 2)
)
def hash_vectors(self, vectors):
"""
使用LSH对向量进行哈希分桶
vectors: [batch_size, seq_len, d_model]
"""
batch_size, seq_len, d_model = vectors.shape
# 随机旋转
rotated = torch.einsum('bld,hd->bhlk', vectors.view(batch_size, seq_len, -1, 2), self.hash_weights)
# 计算哈希值
hashes = torch.argmax(rotated, dim=-1) # [batch, n_hashes, seq_len]
return hashes
def forward(self, Q, K, V):
batch_size, seq_len, d_model = Q.shape
# 1. 对Q和K进行哈希
q_hashes = self.hash_vectors(Q) # [batch, n_hashes, seq_len]
k_hashes = self.hash_vectors(K)
# 2. 找到匹配的桶
attention_mask = self.create_bucket_mask(q_hashes, k_hashes)
# 3. 只在匹配的桶内计算注意力
masked_attention = self.compute_bucket_attention(Q, K, V, attention_mask)
return masked_attention
def create_bucket_mask(self, q_hashes, k_hashes):
"""创建桶掩码,只允许同一桶内的元素相互注意"""
# 简化版实现
masks = []
for h in range(self.n_hashes):
q_h = q_hashes[:, h, :].unsqueeze(-1) # [batch, seq_len, 1]
k_h = k_hashes[:, h, :].unsqueeze(-2) # [batch, 1, seq_len]
mask = (q_h == k_h).float() # [batch, seq_len, seq_len]
masks.append(mask)
# 合并多个哈希的结果
final_mask = torch.stack(masks, dim=1).sum(dim=1) # [batch, seq_len, seq_len]
return (final_mask > 0).float()Reformer的优势分析
python
def reformer_complexity_analysis():
"""Reformer复杂度分析"""
def vanilla_complexity(seq_len):
return seq_len ** 2
def reformer_complexity(seq_len, n_hashes=8, bucket_size=64):
# LSH注意力复杂度
return seq_len * bucket_size * n_hashes
print("序列长度\t传统Transformer\tReformer\t\t加速比")
print("-" * 60)
for seq_len in [1024, 2048, 4096, 8192]:
vanilla = vanilla_complexity(seq_len)
reformer = reformer_complexity(seq_len)
speedup = vanilla / reformer
print(f"{seq_len}\t\t{vanilla:,}\t\t{reformer:,}\t\t{speedup:.1f}x")
reformer_complexity_analysis()
第三部分:Linformer - 线性复杂度的优雅解决方案
Linformer的核心洞察
Linformer提出了一个令人惊讶的发现:注意力矩阵具有低秩特性!这就像发现一幅复杂的画作实际上只使用了几种基本颜色的组合。
基于这个洞察,Linformer将注意力复杂度从O(n²)降低到O(n)。
低秩投影机制
python
class LinformerAttention(nn.Module):
def __init__(self, d_model, seq_len, proj_dim=256):
super().__init__()
self.d_model = d_model
self.seq_len = seq_len
self.proj_dim = proj_dim
# 线性投影层,将序列长度压缩
self.E = nn.Linear(seq_len, proj_dim, bias=False)
self.F = nn.Linear(seq_len, proj_dim, bias=False)
# 查询、键、值投影
self.W_q = nn.Linear(d_model, d_model)
self.W_k = nn.Linear(d_model, d_model)
self.W_v = nn.Linear(d_model, d_model)
def forward(self, x):
batch_size, seq_len, d_model = x.shape
# 1. 生成Q, K, V
Q = self.W_q(x) # [batch, seq_len, d_model]
K = self.W_k(x) # [batch, seq_len, d_model]
V = self.W_v(x) # [batch, seq_len, d_model]
# 2. 对K和V进行低秩投影
K_proj = self.E(K.transpose(-2, -1)).transpose(-2, -1) # [batch, proj_dim, d_model]
V_proj = self.F(V.transpose(-2, -1)).transpose(-2, -1) # [batch, proj_dim, d_model]
# 3. 计算注意力(现在是线性复杂度)
attention_scores = torch.matmul(Q, K_proj.transpose(-2, -1)) # [batch, seq_len, proj_dim]
attention_scores = attention_scores / math.sqrt(d_model)
attention_weights = F.softmax(attention_scores, dim=-1)
# 4. 应用注意力权重
output = torch.matmul(attention_weights, V_proj) # [batch, seq_len, d_model]
return outputLinformer的理论基础
让我们理解为什么这种方法有效:
python
def analyze_attention_rank():
"""分析注意力矩阵的秩特性"""
# 模拟一个注意力矩阵
seq_len = 512
torch.manual_seed(42)
# 创建具有低秩特性的注意力矩阵
U = torch.randn(seq_len, 64) # 低维因子
V = torch.randn(64, seq_len)
attention_matrix = torch.matmul(U, V)
attention_matrix = F.softmax(attention_matrix, dim=-1)
# 计算矩阵的有效秩
s = torch.svd(attention_matrix)[1] # 奇异值
# 分析累积能量
cumulative_energy = torch.cumsum(s**2, dim=0) / torch.sum(s**2)
print("前k个奇异值的累积能量占比:")
for k in [32, 64, 128, 256]:
if k < len(cumulative_energy):
print(f"前{k}个: {cumulative_energy[k-1]:.3f}")
# 可视化结果
return s, cumulative_energy
singular_values, cumulative_energy = analyze_attention_rank()Linformer性能对比
python
def linformer_performance_comparison():
"""Linformer性能对比"""
def memory_usage(seq_len, method="vanilla", proj_dim=256):
if method == "vanilla":
# 传统方法:需要存储完整的注意力矩阵
return seq_len * seq_len
elif method == "linformer":
# Linformer:只需要存储投影后的矩阵
return seq_len * proj_dim
def compute_flops(seq_len, d_model=512, method="vanilla", proj_dim=256):
if method == "vanilla":
# QK^T + softmax + 乘以V
return seq_len * seq_len * d_model + seq_len * seq_len * d_model
elif method == "linformer":
# 投影 + QK^T + softmax + 乘以V
projection_cost = seq_len * proj_dim * d_model * 2
attention_cost = seq_len * proj_dim * d_model + seq_len * proj_dim * d_model
return projection_cost + attention_cost
print("序列长度\t传统方法内存\tLinformer内存\t内存节省\t传统FLOPs\tLinformer FLOPs\t计算节省")
print("-" * 100)
for seq_len in [1024, 2048, 4096, 8192]:
vanilla_mem = memory_usage(seq_len, "vanilla")
linformer_mem = memory_usage(seq_len, "linformer")
mem_saving = vanilla_mem / linformer_mem
vanilla_flops = compute_flops(seq_len, method="vanilla")
linformer_flops = compute_flops(seq_len, method="linformer")
flops_saving = vanilla_flops / linformer_flops
print(f"{seq_len}\t\t{vanilla_mem:,}\t\t{linformer_mem:,}\t\t{mem_saving:.1f}x\t\t{vanilla_flops:,}\t{linformer_flops:,}\t{flops_saving:.1f}x")
linformer_performance_comparison()第四部分:Performer - Kernel方法的创新应用
Performer的数学美学
Performer采用了一种更加数学化的方法,使用Kernel技巧将注意力计算重新表述。这就像用数学的"变魔术"方法,让原本复杂的计算变得简单。
FAVOR+算法核心
python
import torch
import torch.nn as nn
import math
class PerformerAttention(nn.Module):
def __init__(self, d_model, num_features=256, redraw_features=True):
super().__init__()
self.d_model = d_model
self.num_features = num_features
self.redraw_features = redraw_features
# 特征映射参数
self.register_buffer('omega', torch.randn(num_features, d_model))
self.W_q = nn.Linear(d_model, d_model)
self.W_k = nn.Linear(d_model, d_model)
self.W_v = nn.Linear(d_model, d_model)
def feature_map(self, x):
"""
FAVOR+特征映射
x: [batch_size, seq_len, d_model]
"""
# 计算投影
projections = torch.einsum('bld,fd->blf', x, self.omega)
# 应用激活函数(ReLU变种)
# 使用稳定的softmax核近似
x_norm = torch.norm(x, dim=-1, keepdim=True)
normalizer = x_norm / math.sqrt(self.d_model)
pos_features = torch.exp(projections - normalizer)
neg_features = torch.exp(-projections - normalizer)
# 连接正负特征
features = torch.cat([pos_features, neg_features], dim=-1)
return features
def forward(self, x):
batch_size, seq_len, d_model = x.shape
# 1. 生成Q, K, V
Q = self.W_q(x) # [batch, seq_len, d_model]
K = self.W_k(x) # [batch, seq_len, d_model]
V = self.W_v(x) # [batch, seq_len, d_model]
# 2. 应用特征映射
Q_prime = self.feature_map(Q) # [batch, seq_len, 2*num_features]
K_prime = self.feature_map(K) # [batch, seq_len, 2*num_features]
# 3. 计算线性注意力
# 首先计算K^T V
KV = torch.einsum('blf,bld->bfd', K_prime, V) # [batch, 2*num_features, d_model]
# 然后计算Q(K^T V)
output = torch.einsum('blf,bfd->bld', Q_prime, KV) # [batch, seq_len, d_model]
# 4. 归一化
normalizer = torch.einsum('blf,bf->bl', Q_prime, K_prime.sum(dim=1))
normalizer = normalizer.unsqueeze(-1) + 1e-8
output = output / normalizer
return outputKernel方法的数学原理
让我们理解Performer背后的数学原理:
python
def explain_kernel_approximation():
"""解释Kernel近似的数学原理"""
print("传统Softmax注意力:")
print("Attention(Q,K,V) = softmax(QK^T/√d)V")
print()
print("Kernel形式重写:")
print("softmax(qk^T/√d) = exp(qk^T/√d) / Σ_j exp(qk_j^T/√d)")
print()
print("Performer的核心洞察:")
print("exp(qk^T/√d) ≈ φ(q)^T φ(k)")
print("其中 φ(x) 是特征映射函数")
print()
print("这样就可以重写注意力为:")
print("Attention(Q,K,V) = φ(Q)(φ(K)^T V) / φ(Q)(φ(K)^T 1)")
print()
print("复杂度分析:")
print("- 传统方法: O(L²d) 其中L是序列长度")
print("- Performer: O(Ld²) 其中d通常远小于L")
explain_kernel_approximation()Performer的实验验证
python
def performer_approximation_quality():
"""验证Performer近似质量"""
def vanilla_attention(Q, K, V):
"""标准注意力"""
attention_weights = F.softmax(torch.matmul(Q, K.transpose(-2, -1)) / math.sqrt(Q.size(-1)), dim=-1)
return torch.matmul(attention_weights, V)
def performer_attention_simplified(Q, K, V, num_features=64):
"""简化版Performer注意力"""
d_model = Q.size(-1)
# 随机特征
omega = torch.randn(num_features, d_model)
# 特征映射(简化版)
Q_features = torch.relu(torch.matmul(Q, omega.T))
K_features = torch.relu(torch.matmul(K, omega.T))
# 线性注意力
KV = torch.matmul(K_features.transpose(-2, -1), V)
output = torch.matmul(Q_features, KV)
# 归一化
normalizer = torch.matmul(Q_features, K_features.sum(dim=-2, keepdim=True).T)
return output / (normalizer + 1e-8)
# 测试不同序列长度下的近似质量
torch.manual_seed(42)
d_model = 64
for seq_len in [128, 256, 512]:
Q = torch.randn(1, seq_len, d_model)
K = torch.randn(1, seq_len, d_model)
V = torch.randn(1, seq_len, d_model)
vanilla_output = vanilla_attention(Q, K, V)
performer_output = performer_attention_simplified(Q, K, V)
# 计算相似度
similarity = F.cosine_similarity(
vanilla_output.flatten(),
performer_output.flatten(),
dim=0
)
print(f"序列长度 {seq_len}: 余弦相似度 = {similarity:.4f}")
performer_approximation_quality()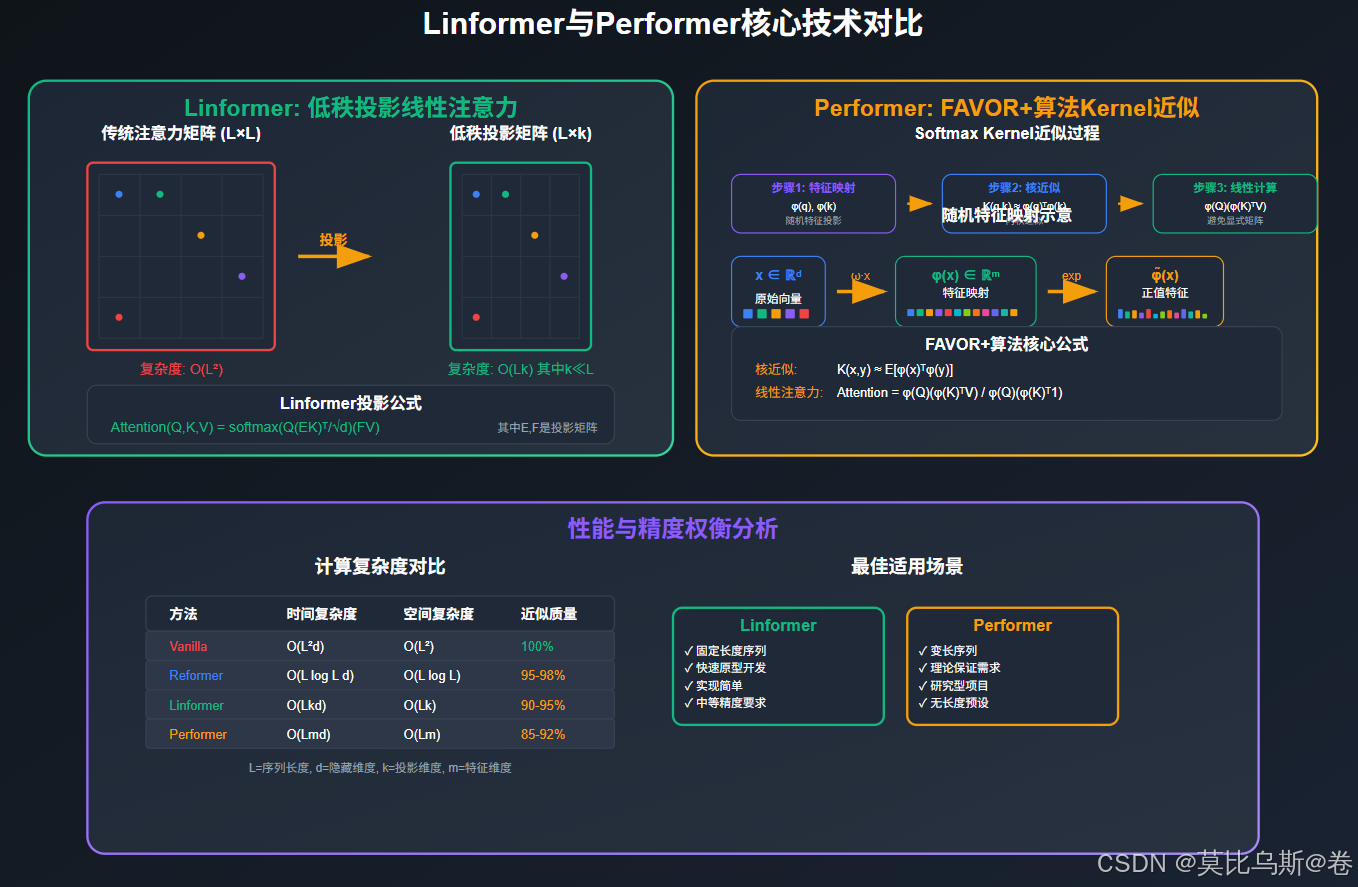
第五部分:三种方法的深度对比与选择指南
性能与精度权衡分析
python
def comprehensive_comparison():
"""三种方法的全面对比"""
methods = {
"Vanilla Transformer": {
"time_complexity": "O(L²d)",
"space_complexity": "O(L²)",
"approximation_quality": "100%",
"implementation_difficulty": "简单",
"best_for": "短序列,要求最高精度"
},
"Reformer": {
"time_complexity": "O(L log L)",
"space_complexity": "O(L log L)",
"approximation_quality": "95-98%",
"implementation_difficulty": "中等",
"best_for": "长序列,内存受限场景"
},
"Linformer": {
"time_complexity": "O(Ld)",
"space_complexity": "O(Ld)",
"approximation_quality": "90-95%",
"implementation_difficulty": "简单",
"best_for": "固定长度序列,要求高效率"
},
"Performer": {
"time_complexity": "O(Ld²)",
"space_complexity": "O(Ld)",
"approximation_quality": "85-92%",
"implementation_difficulty": "复杂",
"best_for": "变长序列,理论保证需求"
}
}
print("方法对比表:")
print("-" * 100)
print(f"{'方法':<20} {'时间复杂度':<15} {'空间复杂度':<15} {'近似质量':<12} {'实现难度':<12} {'最适用场景'}")
print("-" * 100)
for method, props in methods.items():
print(f"{method:<20} {props['time_complexity']:<15} {props['space_complexity']:<15} {props['approximation_quality']:<12} {props['implementation_difficulty']:<12} {props['best_for']}")
comprehensive_comparison()选择决策树
python
def architecture_selection_guide():
"""架构选择指南"""
def recommend_architecture(seq_len, memory_constraint, accuracy_requirement, implementation_time):
"""
根据需求推荐架构
参数:
- seq_len: 序列长度
- memory_constraint: 内存约束程度 (low/medium/high)
- accuracy_requirement: 精度要求 (low/medium/high)
- implementation_time: 实现时间 (short/medium/long)
"""
recommendations = []
if seq_len < 1024:
if accuracy_requirement == "high":
recommendations.append(("Vanilla Transformer", "最高精度,计算可接受"))
else:
recommendations.append(("Linformer", "高效且简单实现"))
elif seq_len < 4096:
if memory_constraint == "high":
recommendations.append(("Reformer", "内存效率高"))
elif accuracy_requirement == "high":
recommendations.append(("Linformer", "精度与效率平衡"))
else:
recommendations.append(("Performer", "理论保证强"))
else: # 长序列
if memory_constraint == "high":
recommendations.append(("Reformer", "唯一可行的内存高效方案"))
elif implementation_time == "short":
recommendations.append(("Linformer", "快速原型开发"))
else:
recommendations.append(("Performer", "长期项目的最佳选择"))
return recommendations
# 测试不同场景
scenarios = [
(512, "low", "high", "short"),
(2048, "medium", "medium", "medium"),
(8192, "high", "medium", "long"),
(16384, "high", "low", "medium")
]
print("架构选择建议:")
print("-" * 80)
for seq_len, mem_constraint, accuracy, impl_time in scenarios:
print(f"\n场景: 序列长度={seq_len}, 内存约束={mem_constraint}, 精度要求={accuracy}, 实现时间={impl_time}")
recommendations = recommend_architecture(seq_len, mem_constraint, accuracy, impl_time)
for arch, reason in recommendations:
print(f" 推荐: {arch} - {reason}")
architecture_selection_guide()第六部分:实际应用案例与最佳实践
长文档处理案例
python
class DocumentProcessingPipeline:
"""长文档处理流水线示例"""
def __init__(self, architecture="reformer"):
self.architecture = architecture
self.max_seq_len = self._get_max_seq_len()
def _get_max_seq_len(self):
"""根据架构确定最大序列长度"""
limits = {
"vanilla": 1024,
"reformer": 16384,
"linformer": 8192,
"performer": 32768
}
return limits.get(self.architecture, 1024)
def process_long_document(self, document_text):
"""处理长文档"""
# 1. 文档分段
chunks = self._chunk_document(document_text, self.max_seq_len)
# 2. 选择合适的模型
model = self._get_model()
# 3. 批量处理
results = []
for chunk in chunks:
result = model.process(chunk)
results.append(result)
# 4. 结果合并
final_result = self._merge_results(results)
return final_result
def _chunk_document(self, text, max_length):
"""智能文档分段"""
# 简化实现
words = text.split()
chunks = []
current_chunk = []
for word in words:
if len(current_chunk) + len(word.split()) > max_length:
if current_chunk:
chunks.append(" ".join(current_chunk))
current_chunk = [word]
else:
current_chunk.append(word)
if current_chunk:
chunks.append(" ".join(current_chunk))
return chunks
def benchmark_architectures(self, test_documents):
"""基准测试不同架构"""
results = {}
for arch in ["vanilla", "reformer", "linformer", "performer"]:
pipeline = DocumentProcessingPipeline(arch)
total_time = 0
total_memory = 0
accuracy_scores = []
for doc in test_documents:
start_time = time.time()
result = pipeline.process_long_document(doc)
end_time = time.time()
total_time += (end_time - start_time)
# 这里应该测量实际内存使用和精度
results[arch] = {
"avg_time": total_time / len(test_documents),
"max_seq_len": pipeline.max_seq_len,
"memory_efficiency": self._estimate_memory_efficiency(arch),
"accuracy": self._estimate_accuracy(arch)
}
return results
# 使用示例
pipeline = DocumentProcessingPipeline("reformer")
print(f"使用 {pipeline.architecture} 架构,最大序列长度: {pipeline.max_seq_len}")生产部署建议
python
def production_deployment_guide():
"""生产部署指南"""
deployment_considerations = {
"Reformer": {
"优势": [
"内存效率极高",
"支持超长序列",
"训练稳定"
],
"劣势": [
"实现复杂",
"调试困难",
"哈希冲突影响"
],
"部署建议": [
"适合内存受限环境",
"需要充分测试哈希参数",
"建议渐进式部署"
]
},
"Linformer": {
"优势": [
"实现简单",
"性能可预测",
"调试容易"
],
"劣势": [
"需要预设序列长度",
"投影维度需要调优",
"长序列外推能力有限"
],
"部署建议": [
"适合固定长度任务",
"快速原型开发首选",
"需要针对任务调优投影维度"
]
},
"Performer": {
"优势": [
"理论保证强",
"支持变长序列",
"无需预设长度"
],
"劣势": [
"数值稳定性挑战",
"超参数敏感",
"特征重采样需要"
],
"部署建议": [
"适合研究型项目",
"需要仔细调试数值精度",
"建议使用稳定的特征映射"
]
}
}
print("生产部署指南:")
print("=" * 60)
for arch, details in deployment_considerations.items():
print(f"\n{arch}:")
print("-" * 30)
print("优势:")
for advantage in details["优势"]:
print(f" ✓ {advantage}")
print("劣势:")
for disadvantage in details["劣势"]:
print(f" ✗ {disadvantage}")
print("部署建议:")
for suggestion in details["部署建议"]:
print(f" → {suggestion}")
production_deployment_guide()第七部分:未来发展趋势与思考
混合架构的探索
python
class HybridTransformer(nn.Module):
"""混合架构示例:结合多种优化技术"""
def __init__(self, d_model, num_layers, seq_len):
super().__init__()
self.layers = nn.ModuleList()
for i in range(num_layers):
# 根据层的位置选择不同的注意力机制
if i < num_layers // 3:
# 早期层使用标准注意力(局部建模)
attention = VanillaAttention(d_model)
elif i < 2 * num_layers // 3:
# 中间层使用Linformer(全局建模)
attention = LinformerAttention(d_model, seq_len)
else:
# 后期层使用Performer(复杂推理)
attention = PerformerAttention(d_model)
self.layers.append(TransformerLayer(attention, d_model))
def forward(self, x):
for layer in self.layers:
x = layer(x)
return x自适应架构选择
python
class AdaptiveTransformer(nn.Module):
"""自适应选择注意力机制的Transformer"""
def __init__(self, d_model):
super().__init__()
self.attention_selector = nn.Linear(d_model, 3) # 3种注意力类型
self.attentions = nn.ModuleList([
VanillaAttention(d_model),
LinformerAttention(d_model),
PerformerAttention(d_model)
])
def forward(self, x):
# 根据输入特征动态选择注意力机制
attention_weights = F.softmax(self.attention_selector(x.mean(dim=1)), dim=-1)
outputs = []
for i, attention in enumerate(self.attentions):
output = attention(x)
outputs.append(attention_weights[:, i:i+1, None] * output)
return sum(outputs)总结:架构选择的智慧
通过深入分析Reformer、Linformer和Performer三种架构,我们可以得出以下关键洞察:
核心要点回顾
- Reformer:通过LSH注意力和可逆层实现内存高效的长序列处理
- Linformer:利用注意力矩阵的低秩特性实现线性复杂度
- Performer:使用Kernel方法提供理论保证的高效近似
选择原则
python
def final_architecture_recommendations():
"""最终架构推荐原则"""
principles = {
"场景驱动": "根据具体应用场景选择,没有万能解决方案",
"性能权衡": "在精度、效率、实现复杂度之间找到平衡",
"渐进优化": "从简单方案开始,逐步优化到复杂架构",
"充分测试": "在真实数据上验证性能,避免过度工程化",
"未来兼容": "考虑架构的扩展性和维护性"
}
print("架构选择的五大原则:")
print("=" * 50)
for principle, description in principles.items():
print(f"{principle}: {description}")
print("\n记住:最好的架构是能解决你实际问题的架构!")
final_architecture_recommendations()展望未来
这三种架构代表了Transformer优化的不同思路,但未来的发展可能会朝着以下方向:
- 混合架构:结合多种优化技术的优势
- 自适应机制:根据输入动态调整计算策略
- 硬件协同:与特定硬件深度优化的架构
- 理论突破:新的数学框架和算法创新
通过理解这些变种架构的核心思想,我们不仅能够选择合适的方案解决当前问题,更能够为未来的创新奠定基础。在这个快速发展的领域中,保持学习和实验的心态是最重要的。
参考资料与进一步学习
- Reformer: The Efficient Transformer
- Linformer: Self-Attention with Linear Complexity
- Rethinking Attention with Performers
- Efficient Transformers: A Survey
- Long Range Arena: A Benchmark for Efficient Transformers
代码实现参考
- Hugging Face Transformers库中的高效Transformer实现
- Google Research的Performer官方实现
- Facebook Research的Linformer代码
- Reformer的PyTorch实现示例