D.滑动树
每次测试时限:2 秒
每次测试的内存限制:256 兆字节
输入:标准输入
输出:标准输出
给你一棵树 ∗^{\text{∗}}∗ ,它有 nnn 个顶点,编号从 111 到 nnn 。您可以使用下面的多步操作(称为滑动操作)来修改它的结构:
- 选择三个不同的 顶点 aaa 、 bbb 和 ccc ,使得 bbb 与 aaa 和 ccc 直接相连。
- 然后,对于 bbb 的每个邻居 ddd (不包括 aaa 和 ccc ),删除 bbb 和{638992}之间的边,将 ddd 直接连接到 ccc 。
例如,下图展示了最左边树中的 a=4a = 4a=4 、 b=3b = 3b=3 和 c=5c = 5c=5 。
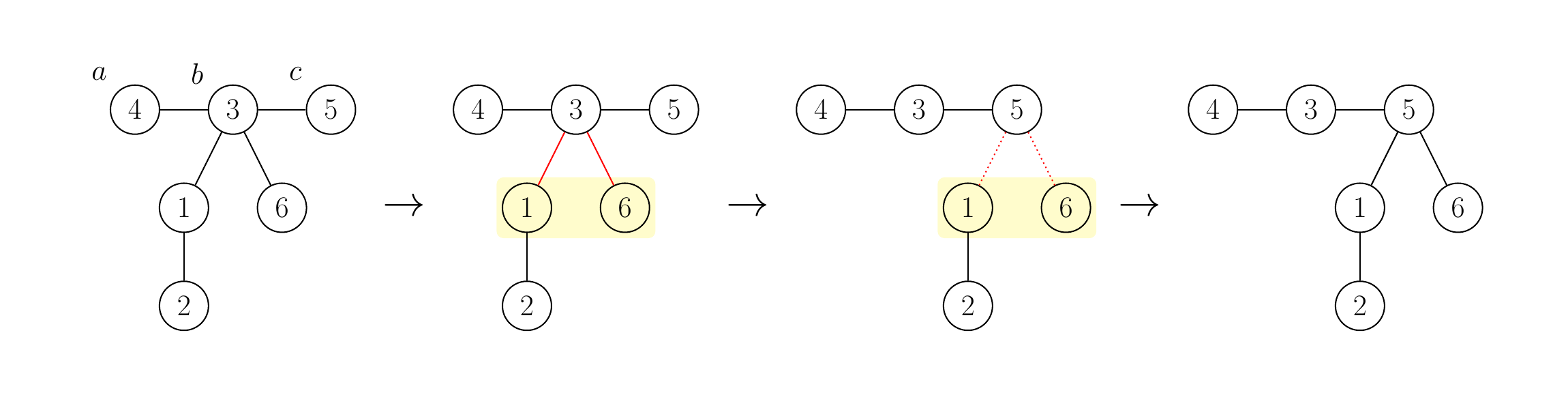
可以证明,经过滑动操作后,得到的图仍然是一棵树。
你的任务是找到一个滑动操作序列,将树状图转化为路径图 †^{\text{†}}† ,同时减少操作的总数。如果至少需要一个操作,你只需要输出最优序列中的**个滑动操作。可以证明,使用有限的操作次数将树转换为路径图是可能的。
∗^{\text{∗}}∗ 树是没有循环的连通图。
†^{\text{†}}† 路径图是每个顶点的度数最多为 222 的树。请注意,只有 111 个顶点而没有边的图也是路径图。
输入
每个测试包含多个测试用例。第一行包含测试用例的数量 ttt ( 1≤t≤1041 \le t \le 10^41≤t≤104 )。测试用例说明如下。
每个测试用例的第一行都包含一个整数 nnn ( 1≤n≤2⋅1051 \le n \le 2 \cdot 10^51≤n≤2⋅105 ) - 树的顶点数。
下面 n−1n-1n−1 行的 iii -th 包含两个整数 uiu_iui 和 viv_ivi ( 1≤ui,vi≤n1 \le u_i,v_i \le n1≤ui,vi≤n , ui≠viu_i \neq v_iui=vi ) - iii -th 边的两端。
可以保证给定的边构成一棵树。
保证所有测试用例中 nnn 的总和不超过 2⋅1052 \cdot 10^52⋅105 。
输出
对于每个测试用例:
- 如果不需要任何操作(即输入树已经是一个路径图),则输出 −1-1−1 。
- 否则,输出三个不同 的整数 aaa 、 bbb 和 ccc ( 1≤a,b,c≤n1 \le a,b,c \le n1≤a,b,c≤n )--最佳序列中第一个滑动操作的选定顶点。
如果第一次操作有多个有效选择,则可以输出其中任意一个。
注
第一个测试案例与问题陈述中提供的示例相符。可以证明,我们无法用少于 222 次的运算将给定的树转化为路径图。
但是,我们可以使用 222 次操作将给定的树转化为路径图:首先,我们对 a=4a=4a=4 、 b=3b=3b=3 和 c=5c=5c=5 进行操作,如示例所示。接下来,我们对 a=3a=3a=3 、 b=5b=5b=5 和 c=6c=6c=6 进行操作。之后,树就变成了路径图。第二个操作如下图所示。
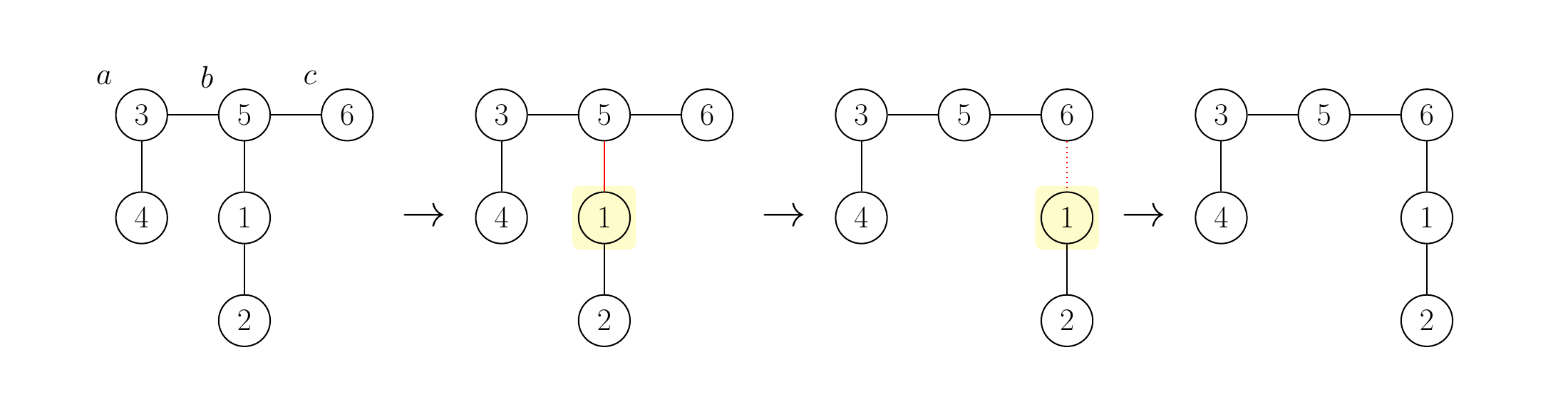
这样,我们就得到了一个操作总数最小的滑动操作序列。但要注意的是,只有第一个操作必须出现在输出中;操作次数和第二个操作不应***出现在输出中。
在第二和第三个测试案例中,树已经是一个路径图,因此不需要任何操作。
题目分析
该代码解决的问题是在一棵树中找到一个特定的节点结构(Y型结构),即存在一个节点,其度大于2,并且位于树的直径上。若树为链状结构(所有节点度不超过2),则直接输出-1。
代码功能
图的输入与初始化:读取树的边信息,构建邻接表。
判断链状结构:检查是否存在度大于2的节点,若不存在则直接输出-1。
求树的直径:通过两次BFS确定树的直径端点(p1和p2)。
标记直径路径:通过BFS标记直径上的所有节点。
寻找Y型结构:遍历直径上的节点,找到度大于2的节点,并输出其相邻节点中的两个(一个在直径上,一个不在)。
关键步骤
树的直径求解:通过两次BFS找到距离最远的两个节点(p1和p2)。
标记直径路径:使用BFS记录从p1到p2的路径。
Y型结构检测:遍历直径上的节点,检查其度是否大于2,并输出符合条件的相邻节点。
代码优化
输入优化:使用ios::sync_with_stdio(false)和cin.tie(0)加速输入输出。
数组初始化:每次测试用例前重置h、in等数组。
提前终止:若检测到链状结构,直接跳过后续处理。
时间复杂度
BFS遍历:每次BFS的时间复杂度为O(N),总时间复杂度为O(N)。
标记直径路径:最坏情况下需要遍历所有节点,时间复杂度为O(N)。
Y型结构检测:遍历直径上的节点,时间复杂度为O(N)。 总体时间复杂度为O(N),适用于大规模数据。
- #(蒻蒻)代码欣赏
cpp
#include<bits/stdc++.h>
#define int long long
#define pi pair<int,int>
using namespace std;
const int N=2e5+5;
int n,p1,p2,tot,h[N],dis[N],ne[N*2],to[N*2],pre[N],in[N];
bool vis[N];
void add(int a,int b)
{
tot++;
ne[tot]=h[a];
h[a]=tot;
to[tot]=b;
}
int bfs(int u)
{
dis[u]=0;
int maxx=0;
int id=u;
queue<pi>q;
q.push({u,0});
while(!q.empty())
{
int j=q.front().first;
int fa=q.front().second;
q.pop();
for(int i=h[j];i;i=ne[i])
{
int jj=to[i];
if(jj!=fa)
{
dis[jj]=dis[j]+1;
q.push({jj,j});
if(dis[jj]>maxx)
{
maxx=dis[jj];
id=jj;
}
}
}
}
return id;
}
void zhijing()
{
p1=bfs(1);
p2=bfs(p1);
}
void biaoji()
{
queue<pi>q;
q.push({p1,0});
while(!q.empty())
{
int j=q.front().first;
int fa=q.front().second;
if(j==p2)
break;
q.pop();
for(int i=h[j];i;i=ne[i])
{
int jj=to[i];
if(jj!=fa)
{
pre[jj]=j;
q.push({jj,j});
}
}
}
fill(vis+1,vis+1+n,0);
int js=p2;vis[p1]=1;
while(js!=p1)
{
vis[js]=1;
js=pre[js];
}
return;
}
signed main()
{
ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
int _,a,b;
cin>>_;
while(_--)
{
cin>>n;
fill(h+1,h+1+n,0);
fill(in+1,in+1+n,0);
tot=0;bool flag=0;
for(int i=1;i<n;i++)
{
cin>>a>>b;
in[a]++,in[b]++;
add(a,b);add(b,a);
}
for(int i=1;i<=n;i++)
{
if(in[i]>2)
break;
if(i==n)
{
cout<<"-1"<<'\n';flag=1;
}
}
if(flag)continue;
zhijing();
biaoji();
for(int i=1;i<=n;i++)
{
int id1=0,id2=0,id3=0;
if(vis[i]&&in[i]>2)
{
id1=i;
for(int j=h[i];j;j=ne[j])
{
int jj=to[j];
if(vis[jj])
id2=jj;
if(!vis[jj])
id3=jj;
if(id2&&id3)
{
cout<<id2<<" "<<id1<<" "<<id3<<'\n';
flag=1;break;
}
}
if(flag)break;
}
}
}
return 0;
}