python自学笔记14 NumPy 线性代数

在Numpy库中有专门的linalg 模块用来做线性代数相关的运算。

本文中线性代数的一般概念不会解释

拆解矩阵

鸢尾花数据矩阵结构如下（150 × 4）：

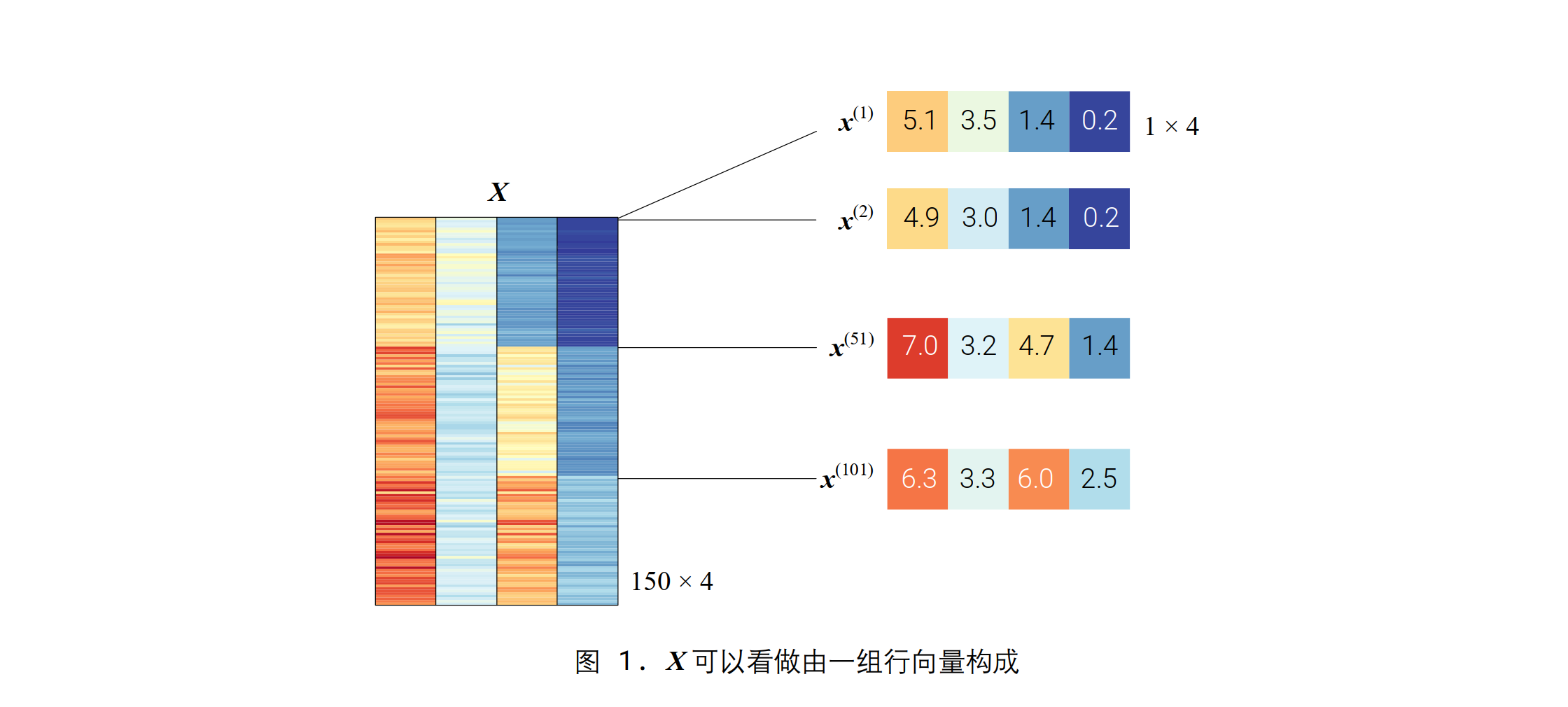
取其中的行向量和列向量：

python 复制代码

# 导入包
import numpy as np
from sklearn.datasets import load_iris
# 从sklearn导入鸢尾花数据
iris = load_iris()
X = iris.data
# 提取四个行向量 (二维数组)
x_row_1 = X[[1 - 1], :]
x_row_2 = X[[2 - 1], :]
x_row_51 = X[[51 - 1], :]
x_row_101 = X[[101 - 1], :]

# 提取四个列向量 (二维数组)
x_col_1 = X[:, [0]]
x_col_2 = X[:, [1]]
x_col_3 = X[:, [2]]
x_col_4 = X[:, [3]]

向量运算

向量的模

python 复制代码

norm_x_row_1 = np.linalg.norm(x_row_1)
norm_x_row_2 = np.linalg.norm(x_row_2)
norm_x_row_51 = np.linalg.norm(x_row_51)
norm_x_row_101 = np.linalg.norm(x_row_101)

向量单位化

python 复制代码

unit_x_row_1 = x_row_1 / norm_x_row_1
unit_x_row_2 = x_row_2 / norm_x_row_2
unit_x_row_51 = x_row_51 / norm_x_row_51
unit_x_row_101 = x_row_101 / norm_x_row_101

向量内积

python 复制代码

inner_prod_x_row_1_2 = np.dot(x_row_1[0], x_row_2[0])
inner_prod_x_row_1_51 = np.dot(x_row_1[0], x_row_51[0])
inner_prod_x_row_1_101 = np.dot(x_row_1[0], x_row_101[0])

向量夹角

下面的代码先求内积是因为单位向量的内积就是余弦值

python 复制代码

# 计算单位向量内积
dot_product_1_51 = np.dot(unit_x_row_1[0],
						  unit_x_row_51[0])
# 将结果转化为弧度
angle_1_51 = np.arccos(dot_product_1_51)
# 将结果转化为角度
angle_1_51 = np.rad2deg(angle_1_51)

这里补充一个数学上的概念：

矩阵运算

矩阵乘法

python 复制代码

# 第一个格拉姆矩阵
G = X.T @ X
# 第二个格拉姆矩阵
H = X @ X.T

矩阵的逆

python 复制代码

# 计算格拉姆矩阵G的逆矩阵
a G_inv = np.linalg.inv(G)

几个常见矩阵分解

Cholesky 分解

python 复制代码

# 对格拉姆矩阵G进行Cholesky分解
a L = np.linalg.cholesky(G)

G是正定阵

特征值分解 EVD

python 复制代码

# 对格拉姆矩阵G进行特征值分解
Lambdas, V = np.linalg.eig(G)

Lambdas的对角线是特征值，V的每一列是特征向量

奇异值分解 SVD

python 复制代码

# 鸢尾花数据矩阵X奇异值分解
U,S,VT = np.linalg.svd(X, full_matrices = False)