今天我们来学习新的C++算法思想:前缀和
相关题解代码已经上传至作者的个人gitee:CPP 学习代码库: C++代码库新库,旧有C++仓库满员了喜欢请支持以下谢谢
目录
[1. 快速区间求和](#1. 快速区间求和)
[2. 解决子数组相关问题](#2. 解决子数组相关问题)
[3. 多维前缀和](#3. 多维前缀和)
[C++ 中的取模运算](#C++ 中的取模运算)
[Java 中的取模运算](#Java 中的取模运算)
[使用标准库函数(C++17 及以上)](#使用标准库函数(C++17 及以上))
前缀和算法详解
前缀和(Prefix Sum)是一种常用的预处理技术,用于高效处理数组区间求和问题。通过预先计算并存储部分和,可以将区间查询的时间复杂度从O(n)降低到O(1)。
基本概念
前缀和数组定义为:对于给定数组arr,其前缀和数组prefix中,prefix[i]表示arr[0]到arr[i-1]的元素之和(有些实现中可能包含arr[i]本身,具体取决于实现方式)。
构建方法
- 初始化一个与原数组等长的前缀和数组
prefix prefix[0] = arr[0](或0,取决于边界处理)
cpp
原数组: [1, 2, 3, 4, 5]
前缀和数组: [0, 1, 3, 6, 10, 15] // 包含一个初始0应用场景
1. 快速区间求和
给定区间[L, R]的和可以通过prefix[R+1] - prefix[L]快速计算:
- 传统方法:遍历数组,时间复杂度O(n)
- 前缀和方法:直接计算差值,时间复杂度O(1)
2. 解决子数组相关问题
如"和为k的子数组数量"、"最大子数组和"等问题:
- 使用前缀和配合哈希表可以达到O(n)时间复杂度
- 示例:求数组中和为k的连续子数组个数
- 计算前缀和数组
- 使用哈希表记录前缀和出现次数
- 遍历时检查
当前前缀和 - k是否在哈希表中
3. 多维前缀和
可以扩展到二维甚至更高维度:
- 二维前缀和用于快速计算矩形区域和
- 构建方法:
prefix[i][j] = prefix[i-1][j] + prefix[i][j-1] - prefix[i-1][j-1] + arr[i][j] - 查询方法:通过四个角的prefix值相加减得到矩形和
复杂度分析
- 预处理时间复杂度:O(n)
- 空间复杂度:O(n)
- 查询时间复杂度:O(1)
变种与应用示例
差分数组
前缀和的逆运算,用于高效处理区间更新:
- 构建差分数组
diff,其中diff[i] = arr[i] - arr[i-1] - 区间
[L,R]增加val:diff[L] += val,diff[R+1] -= val - 通过差分数组的前缀和恢复原数组
1、前缀和
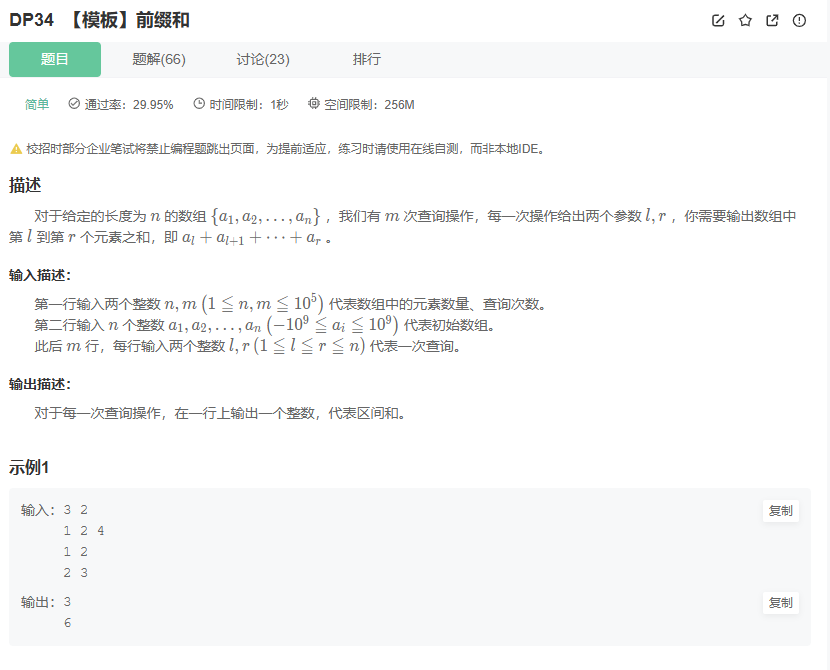
算法思想:
1、预处理出前缀和数组
dp[i]:1到i所有元素的和
dp[i]=dp[i-1]+arr[i]
2、使用前缀和数组
l,r\]所有元素和==dp\[l\]-dp\[r-1
细节问题:为什么要从1开始计数?
为了处理边界情况,添加虚拟结点。如果从0开始计数,想询问0到2算得是dp[2]-dp[-1].
cpp
#include <iostream>
#include<vector>
using namespace std;
int main()
{
//读入数据
int n,q;
cin>>n>>q;
vector<int> arr(n+1);
for(int i=1;i<=n;i++) cin>>arr[i];
//预处理前缀和数组
vector<long long> dp(n+1);//用long long防止溢出
for(int i=1;i<=n;i++) dp[i]=dp[i-1]+arr[i];
//使用前缀和数组
int l=0,r=0;
while(q--)
{
cin>>l>>r;
cout<<dp[r]-dp[l-1]<<endl;
}
return 0;
}
// 64 位输出请用 printf("%lld")2、二维前缀和


算法思想:
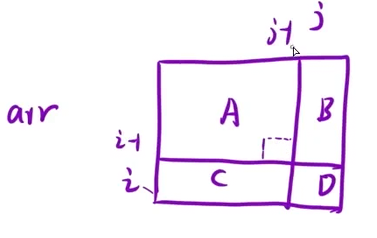
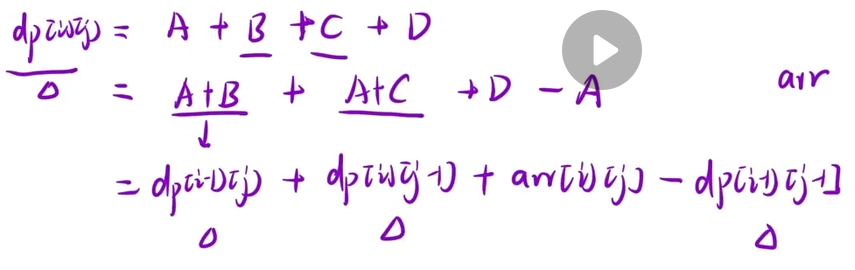
1、预处理一个前缀和矩阵
dp[i,j]:表示从[1,1]到[i,j]所有元素的和
2、使用前缀和矩阵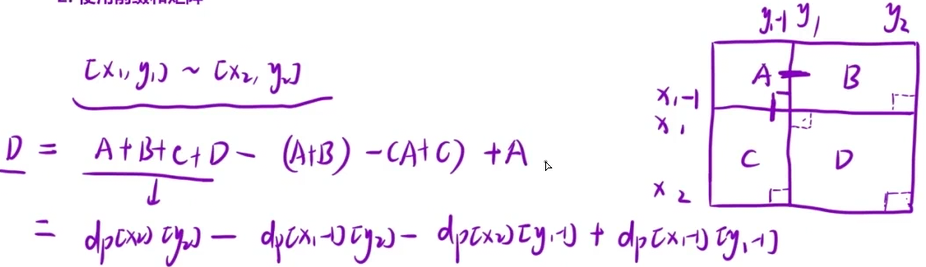
cpp
#include <iostream>
#include<vector>
using namespace std;
int main()
{
//读入数据
int n=0,m=0,q=0;
cin>>n>>m>>q;
vector<vector<int>> arr(n+1,vector<int>(m+1));//矩阵
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
cin>>arr[i][j];
//预处理前缀和矩阵
vector<vector<long long>> dp(n+1,vector<long long >(m+1));
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
dp[i][j]=dp[i-1][j]+arr[i][j]+dp[i][j-1]-dp[i-1][j-1];
//计算处理前缀和矩阵
int x1=0,x2=0,y1=0,y2=0;
while(q--)
{
cin>>x1>>y1>>x2>>y2;
cout<<dp[x2][y2]-dp[x1-1][y2]-dp[x2][y1-1]+dp[x1-1][y1-1]<<endl;
}
return 0;
}3、寻找数组的中心下标

算法思想:
1、预处理前缀和和后缀和数组
前缀和:f[i] 0到i-1之间的和
f[i]=f[i-1]+nums[i-1]
后缀和:g[i] i+1到n-1之间的和
g[i]=g[i+1]+nums[i+1]
2、枚举0到n-1所有下标i,找到f[i]==g[i]
细节问题:初始化
要计算f(0)=0,g(0)=0
f从左向右,g从右向左
cpp
class Solution {
public:
int pivotIndex(vector<int>& nums)
{
int n=nums.size();
vector<int> f(n),g(n);
//预处理前缀和和后缀和数组
for(int i=1;i<n;i++)
f[i]=f[i-1]+nums[i-1];
for(int i=n-2;i>=0;i--)
g[i]=g[i+1]+nums[i+1];
//使用
for(int i=0;i<n;i++)
{
if(f[i]==g[i])
return i;
}
return -1;
}
};4、除自身以外数组的乘积

算法思想:
1、前缀积
前缀积:f[i] 0到i-1之间的积
f[i]=f[i-1]*nums[i-1]
后缀积:g[i] i+1到n-1之间的积
g[i]=g[i+1]*nums[i+1]
2、枚举0到n-1所有下标i,找到f[i]==g[i]
f从左向右,g从右向左
细节:f(0)=1, g(n-1)=1
cpp
class Solution {
public:
vector<int> productExceptSelf(vector<int>& nums)
{
int n=nums.size();
vector<int> f(n),g(n);
f[0]=1,g[n-1]=1;
//预处理前缀和和后缀和数组
for(int i=1;i<n;i++)
f[i]=f[i-1]*nums[i-1];
for(int i=n-2;i>=0;i--)
g[i]=g[i+1]*nums[i+1];
//使用
vector<int> ret(n);
for(int i=0;i<n;i++)
{
ret[i]=f[i]*g[i];
}
return ret;
}
};5、和为k的子数组

算法思想:
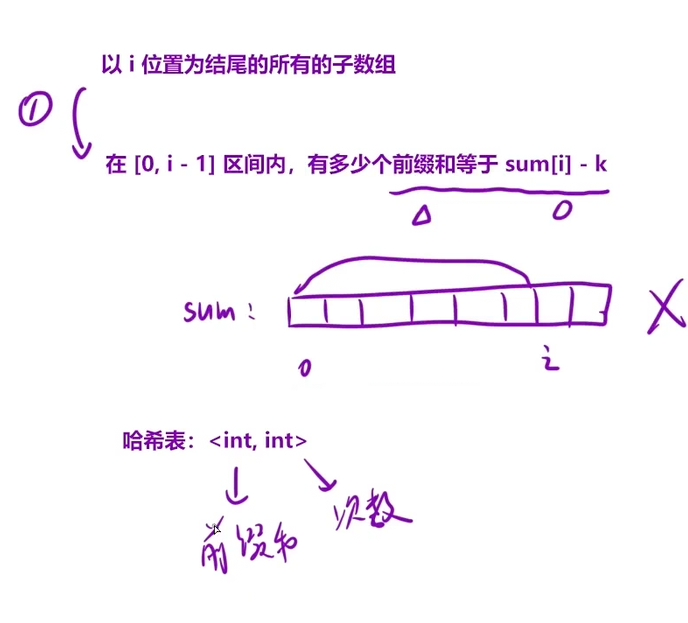
细节问题:
1、前缀和加入哈希的时机
计算i的位置之前,只保存[0,i-1]的前缀和
2、不用真的创建前缀和数组
用sum标记前一个位置的前缀和
cpp
class Solution {
public:
int subarraySum(vector<int>& nums, int k)
{
unordered_map<int,int> hash;//统计出现的次数
hash[0]=1;
int sum=0,ret=0;
for(auto&x:nums )
{
sum+=x;//计算当前位置前缀和
if(hash.count(sum-k)) ret+=hash[sum-k];//统计个数
hash[sum]++;
}
return ret;
}
};6、和可以被k整除的子数组(某一年蓝桥杯原题)

算法思想:前缀和+哈希表
在[0,i-1]找到右多少个前缀和的余数等于sum%k【(sum%k+k)%k】
cpp
class Solution {
public:
int subarraysDivByK(vector<int>& nums, int k)
{
//前缀和的余数
unordered_map<int,int> hash;
hash[0%k]=1;//处理0的余数
int sum=0,ret=0;
for(auto&x:nums)
{
sum+=x;//当前位置余数
int r=(sum%k+k)%k;//修正后的余数
if(hash.count(r)) ret+=hash[r];//统计结果
hash[r]++;
}
return ret;
}
};同余定理:
正式定义:
对于三个整数 a, b, m (其中 m > 0),如果 a 和 b 除以 m 所得的余数相同 ,那么我们就说 a 和 b 对模 m 同余。
记作:
a ≡ b (mod m)
假设有 a ≡ b (mod m) 和 c ≡ d (mod m),那么:
| 性质 | 公式 | C++ 代码操作提示 |
|---|---|---|
| 加法 | a + c ≡ b + d (mod m) |
(a + c) % m 等价于 ( (a % m) + (c % m) ) % m |
| 减法 | a - c ≡ b - d (mod m) |
(a - c) % m 等价于 ( (a % m) - (c % m) + m) % m (注意加 m 是为了防止负数) |
| 乘法 | a * c ≡ b * d (mod m) |
(a * c) % m 等价于 ( (a % m) * (c % m) ) % m |
| 幂运算 | aⁿ ≡ bⁿ (mod m) |
通过快速幂算法计算,基于乘法性质 |
⚠️ 重要警告:除法没有直接性质!
a / c ≡ b / d (mod m) 并不成立 !除法需要用到模逆元 的概念,这需要 c 和 m 互质(gcd(c, m) == 1)。这是一个进阶话题,但非常重要。
| 数学概念 | C++ 程序员的解读 |
|---|---|
| a ≡ b (mod m) | a 和 b 在 % m 操作下的结果是等价的 |
| 同余的性质 | 允许我们在计算过程中随时取模 ,就像拆括号一样 (a op b) % m = ((a % m) op (b % m)) % m(op 为 +, -, *) |
| 核心价值 | 将对大数的操作,转化为对一系列小余数的操作 ,从而避免整数溢出,使得一些原本不可能的计算成为可能。 |
C++/Java中负数%正数的结果及其修正:
C++ 中的取模运算
在 C++ 中,取模运算的结果符号与被除数 (a) 相同:
| 表达式 | 结果 | 解释 |
|---|---|---|
7 % 3 |
1 |
正数取模,正常行为 |
-7 % 3 |
-1 |
结果符号与被除数相同 |
7 % -3 |
1 |
结果符号与被除数相同 |
-7 % -3 |
-1 |
结果符号与被除数相同 |
Java 中的取模运算
在 Java 中,取模运算的结果符号与除数 (b) 相同:
| 表达式 | 结果 | 解释 |
|---|---|---|
7 % 3 |
1 |
正数取模,正常行为 |
-7 % 3 |
-1 |
结果符号与除数相同 |
7 % -3 |
1 |
结果符号与除数相同 |
-7 % -3 |
-1 |
结果符号与除数相同 |
数学上的期望行为
在数学中,我们通常期望取模运算的结果始终是非负的,并且在 [0, |b|-1] 范围内。例如:
-
-7 mod 3应该等于2(因为-7 = (-3)*3 + 2) -
7 mod -3应该等于1(因为7 = (-2)*(-3) + 1)
cpp
// C++ 修正函数
int mod(int a, int b) {
int r = a % b;
// 如果余数为负,加上除数使其为正
if (r < 0) {
r += (b < 0) ? -b : b; // 确保加上的是正除数
}
return r;
}
java
// Java 修正函数
public static int mod(int a, int b) {
int r = a % b;
// 如果余数为负,加上除数使其为正
if (r < 0) {
r += (b < 0) ? -b : b;
}
return r;
}针对特定情况的简化修正
如果确定除数 b 是正数,可以使用更简单的修正:
cpp
// 当 b > 0 时的简化修正
int mod_positive(int a, int b) {
int r = a % b;
return (r < 0) ? r + b : r;
}使用标准库函数(C++17 及以上)
C++17 引入了 std::div 函数族,可以提供符合数学定义的除法结果
cpp
#include <cstdlib>
std::div_t result = std::div(-7, 3);
int remainder = result.rem; // 结果为 2(符合数学定义)7、连续数组

算法思想:前缀和+哈希表
1、将所有的0改为-1
2、在原数组中找到最长的子数组,使子数组中所有元素为0.
与之前的和为k的子数组类似
细节问题:
1、哈希表中一个存前缀和一个存下标
2、存入哈希表的时机:使用后丢入哈希表
3、如果有重复<sum,i>如何存?只保留前面的一对
4、默认前缀和为0的情况如何存储?hash[0]=-1
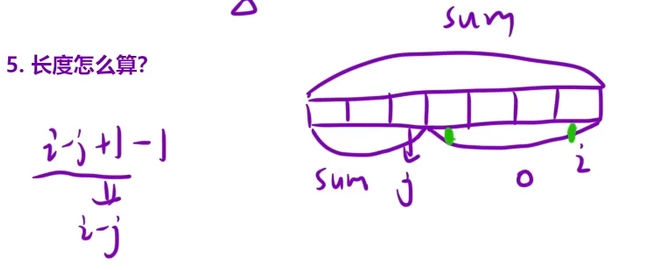
5、长度如何计算?如下图所示,i-j
cpp
class Solution {
public:
int findMaxLength(vector<int>& nums)
{
unordered_map<int,int>hash;
hash[0]=-1;//默认前缀和为0的情况
int sum=0,ret=0;
for(int i=0;i<nums.size();i++)
{
sum+=nums[i]==0?-1:1;//将所有的0改成-1
if(hash.count(sum)) ret=max(ret,i-hash[sum]);
else hash[sum]=i;//去重
}
return ret;
}
};8、矩阵区域和

算法思想:
题目解析:
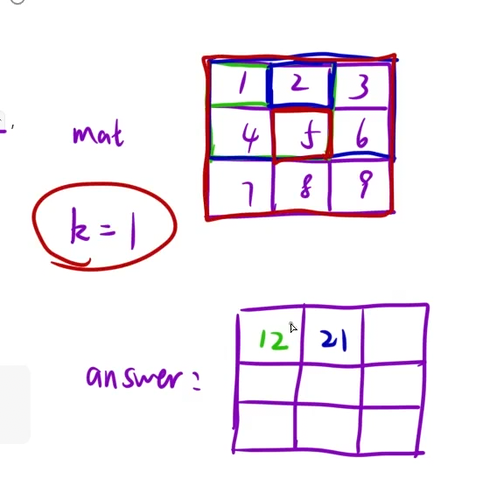
和之前的二维前缀和一样
1、预处理前缀和矩阵。dp[i][j]=dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1]+mat[i-1][j-1]
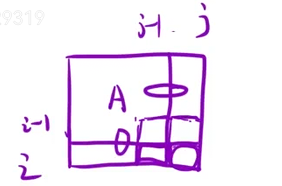
2、使用矩阵
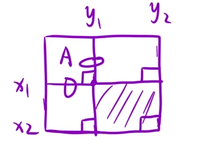
ret[i][j]=dp[x2][y2]-dp[x1-1][y2]-dp[x2][y1-1]+dp[x1-1][y1-1]
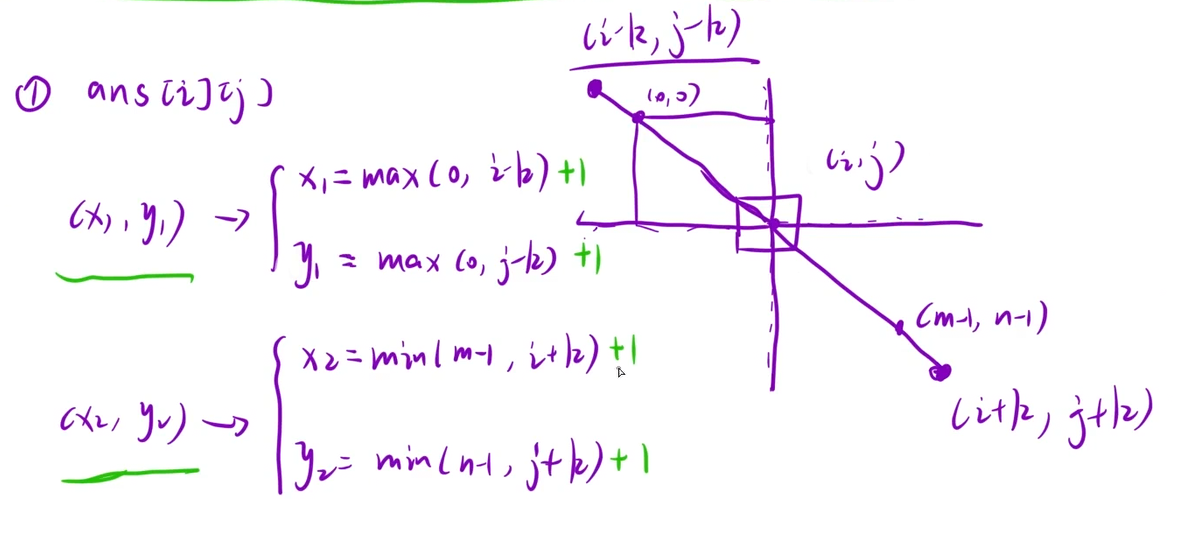
1、求ans[i][j]
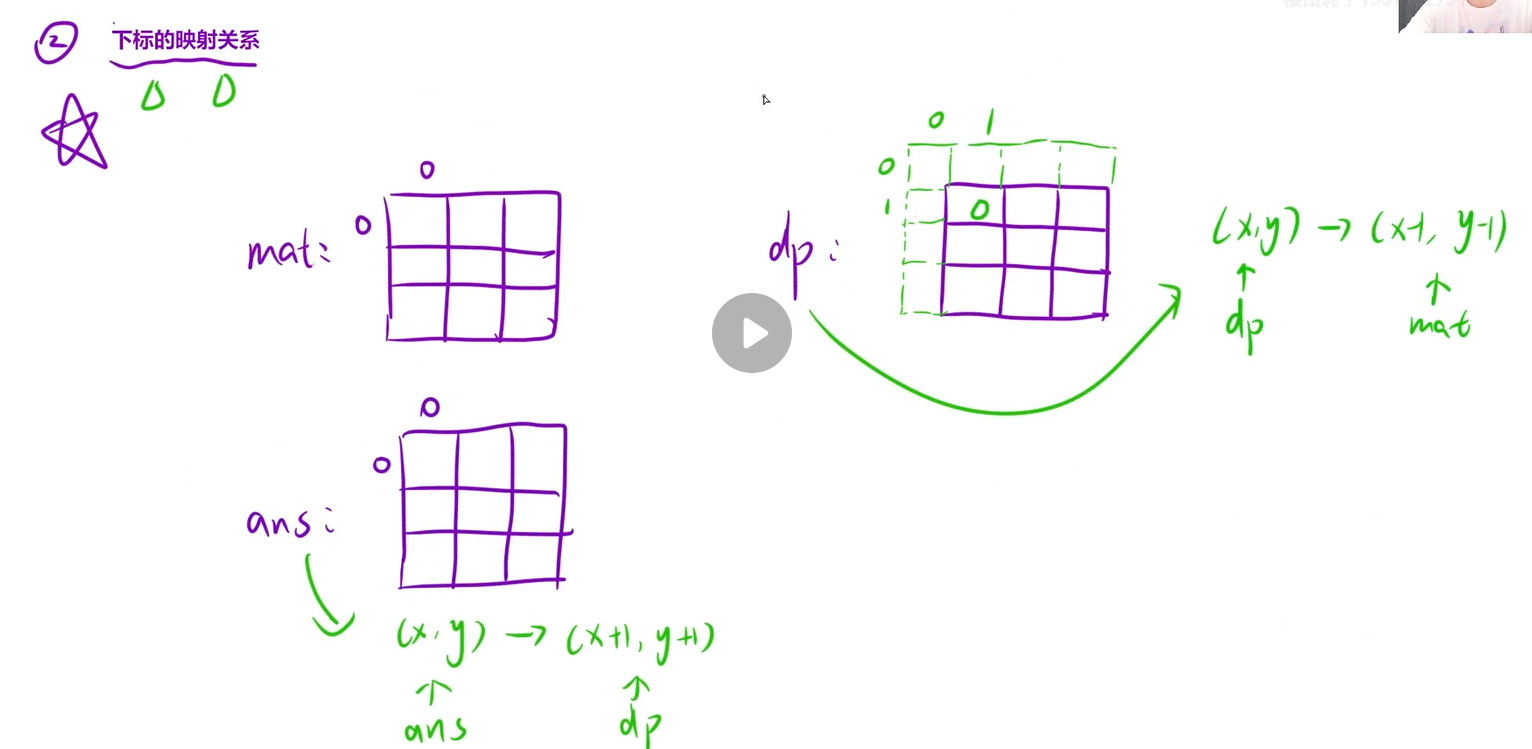
2、下标的映射关系
dp扩充一行一列来简化代码
cpp
class Solution {
public:
vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k)
{
int m=mat.size(),n=mat[0].size();
//1、预处理前缀和矩阵
vector<vector<int>>dp(m+1,vector<int>(n+1));
for(int i=1;i<=m;i++)
for(int j=1;j<=n;j++)
dp[i][j]=dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1]+mat[i-1][j-1];
//使用
vector<vector<int>>ret(m,vector<int>(n));
for(int i=0;i<m;i++)
for(int j=0;j<n;j++)
{
int x1=max(0,i-k)+1,y1=max(0,j-k)+1,x2=min(m-1,i+k)+1,y2=min(n-1,j+k)+1;
ret[i][j]=dp[x2][y2]-dp[x1-1][y2]-dp[x2][y1-1]+dp[x1-1][y1-1];
}
return ret;
}
};本期内容到这里结束了喜欢请点个赞支持一下,谢谢。