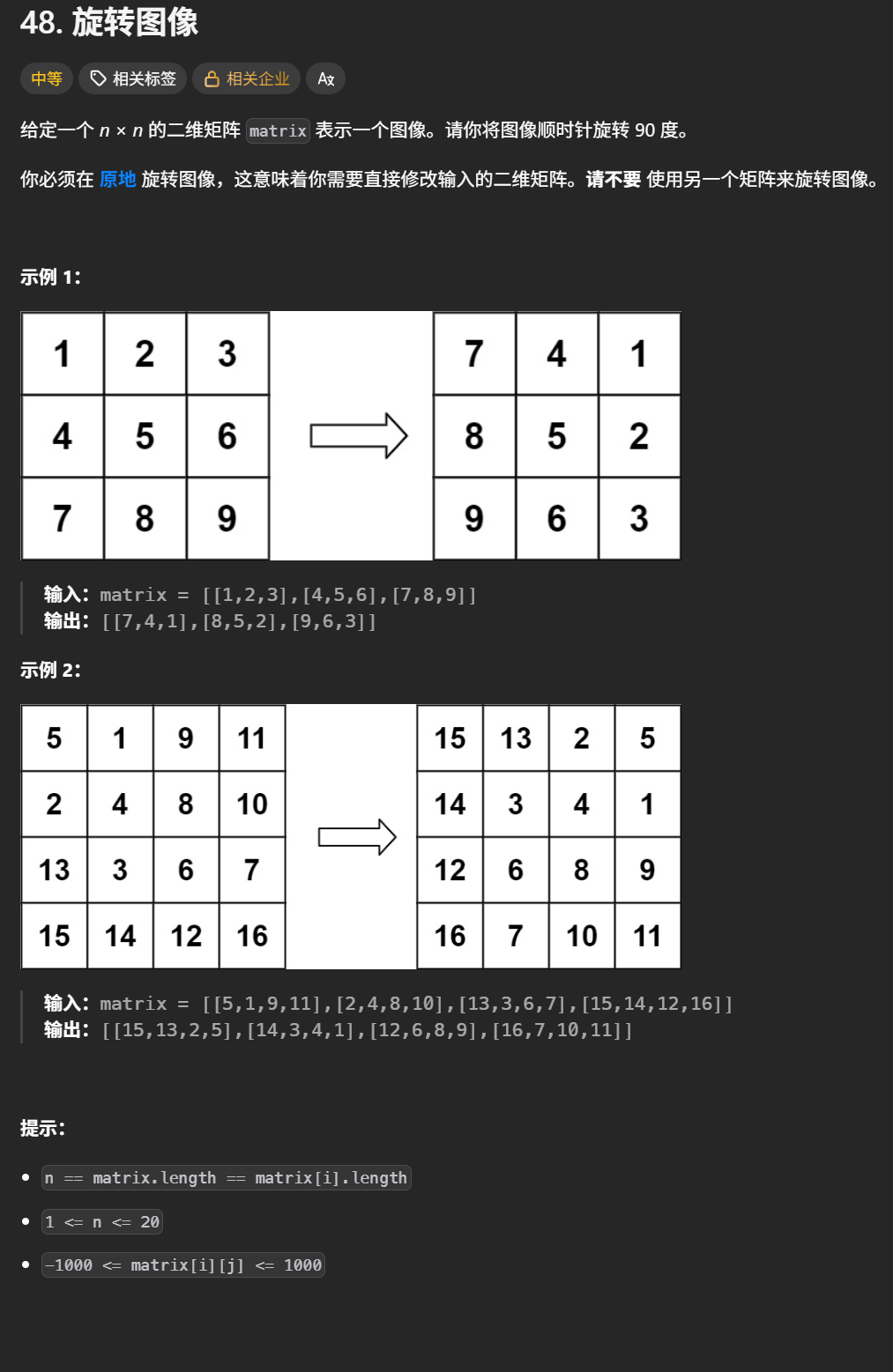
1.题目要求:把一个方阵(n * n的矩阵)顺时针旋转90°。且要求不能创建另一个矩阵,空间复杂度必须是O(1)。
2.思路:
(1)顺时针旋转90°后,位于(i,j)的元素去哪了?
(2)竖着看:
------第一列的元素去到第一行。
------第二列的元素去到第二行。
------......
------第j列的元素去到第j行。
(3)横着看:
------第一行的元素去到最后一列。
------第二行的元素去到倒数第二列。
------......
------第i行的元素去到第n - 1 - i列(i从0开始)。
(4)所以位于第i行第j列的元素,去到第j行第n - 1 - i列,即(i,j)->(j,n - 1 - i)。
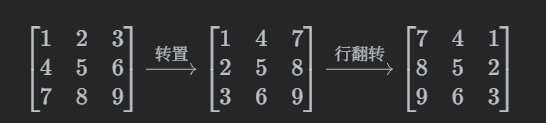
(5)(i,j)->(j,n - 1 - i)可以通过两次翻转操作得到:(i,j)->(转置)(j,i)->(行翻转)(j,n - 1 - i)。
------转置:就是把矩阵按照主对角线翻转,位于(i,j)的元素去到(j,i)。
------行翻转:就是把每一行都翻转,位于(j,i)的元素去到(j,n - 1 - i)。
(6)示例一的操作过程如下图所示:

(7)实现:以下两步操作都可以原地实现。
------转置:把主对角线下面的元素matrix[i][j]和(关于主对角线)对称位置的元素matrix[j][i]交换。
------行翻转:遍历每一行row = matrix[i],把左半边的元素row[j]和(关于垂直中轴)对称位置的元素row[n - 1 - j]交换。或者使用库函数翻转row。
3.复杂度分析:
(1)时间复杂度:O(n^2),其中n是matrix的行数和列数。
(2)空间复杂度:O(1)。
附代码:
(一)写法一:
java
class Solution {
public void rotate(int[][] matrix) {
int n = matrix.length;
//第一步:转置
for(int i = 0;i < n;i++){
for(int j = 0;j < i;j++){ //遍历对角线下方元素
int tmp = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = tmp;
}
}
//第二步:行翻转
for(int i = 0;i < n;i++){ //for(int[] row : matrix)
for(int j = 0;j < n / 2;j++){ //遍历左半元素
int tmp = matrix[i][j]; //int tmp = row[j];
matrix[i][j] = matrix[i][n - 1 - j]; //row[j] = row[n - 1 - j];
matrix[i][n - 1 - j] = tmp; //row[n - 1 - j] = tmp;
}
}
}
}(二)写法二:可以把两个循环合并成一个循环。需要把遍历顺序调整为遍历对角线上方的元素,这样每行遍历完之后,这一行的元素后面就不会再被访问到,可以直接做行翻转(因为在转置过程中,当处理到第i行时,第0到第i - 1行已经完成了它们所有的转置交换,并且已经翻转过了,不会再被修改,所以我们可以安全地修改第i行)。
java
class Solution {
public void rotate(int[][] matrix) {
int n = matrix.length;
for(int i = 0;i < n;i++){
for(int j = i + 1;j < n;j++){ //遍历对角线上方的元素,做转置
int tmp = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = tmp;
}
for(int j = 0;j < n/2;j++){ //遍历左半元素,做行翻转
int tmp = matrix[i][j];
matrix[i][j] = matrix[i][n - 1 - j];
matrix[i][n - 1 - j] = tmp;
}
}
}
}