文章目录
- 题目描述
- 为什么这道题值得你用几分钟的时间弄懂?
- 二分的依据
- 二分的两种不同思路
-
- [右端点(nums[nums.size() - 1])](#右端点(nums[nums.size() - 1]))
- 左端点(nums[0])
- 细节总结
- 下题预告


题目描述
题目链接:
力扣153.寻找旋转排序数组中的最小值
题目描述:
示例 1:
输入:nums = [3,4,5,1,2]
输出:1
解释:原数组为 [1,2,3,4,5] ,旋转 3 次得到输入数组。
示例 2:输入:nums = [4,5,6,7,0,1,2]
输出:0
解释:原数组为 [0,1,2,4,5,6,7] ,旋转 4 次得到输入数组。
示例 3:输入:nums = [11,13,15,17]
输出:11
解释:原数组为 [11,13,15,17] ,旋转 4 次得到输入数组。
提示:1.n == nums.length
2.1 <= n <= 5000
3.-5000 <= nums[i] <= 5000
4.nums 中的所有整数 互不相同
5.nums 原来是一个升序排序的数组,并进行了 1 至 n 次旋转
为什么这道题值得你用几分钟的时间弄懂?
首先这道题的细节思路差异有很多,当我们完全理清细节上的差异时,会对二分查找有更深刻的理解。其次,这道题利用"数组旋转后仍保留部分单调性"的性质来分析二段性,这个逻辑比基础二分查找稍难理解------它不是直接对"整体有序"的数组操作,而是对"局部有序、分段有序"的数组拆解,能帮你突破对二分查找的固有认知。
我不会着重讨论二分查找的通用细节(如 mid 计算方式、循环终止条件等),如果是第一次接触我的博客,建议先从这篇基础博客开始力扣 704.二分查找 基础二分查找,可以进入我的主页这段时间我做的题目都是关于二分查找的,可以从上面的那个博客往后看相信会让你对二分理解的更加深刻;如果是一直跟进的老朋友,直接往下看即可,逻辑衔接会很顺畅。
二分的依据
这道题乍看数组"忽高忽低",似乎无法用二分,但核心关键在于:旋转前的数组是严格单调递增的,旋转后仍会保留"两段单调递增"的特性------我们可以基于这个特性找到"二段性",进而用二分解决问题。
具体来说,旋转后的数组只会出现两种情况:
- 未发生有效旋转(或旋转后回到原状态) :数组仍为整体单调递增,例如
[11,13,15,17] - 发生有效旋转 :数组被拆分为左右两段独立的单调递增子数组,且左段的所有元素都大于 右段的所有元素。例如
[4,5,6,7,0,1,2]拆分为左段[4,5,6,7]和右段[0,1,2],左段最小值4大于右段最大值2,如下图👇(左段[4,5,6,7]对应AB ,右段[0,1,2]对应CD)
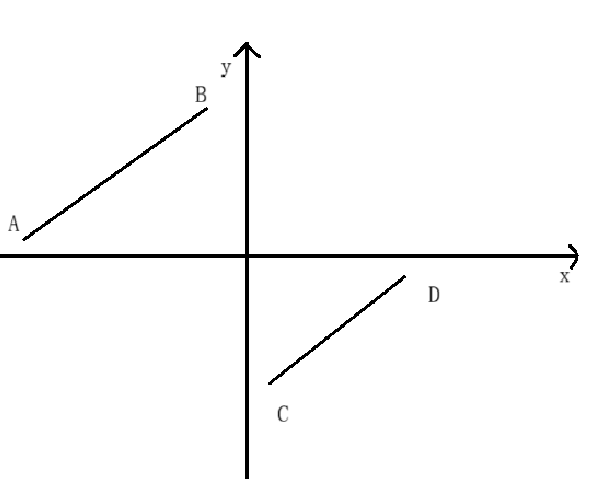
正是这种"要么整体有序,要么两段有序且左段>右段"的特性,为二分查找提供了判断依据------我们可以通过与数组的端点值对比,确定最小值所在的区间,进而缩小范围。
二分的两种不同思路
上面我们确定了数组的二段性,接下来关键是"如何利用端点值划分区间"。这里有两种核心思路:以右端点 为基准,或以左端点为基准。
右端点(nums[nums.size() - 1])
首先明确一个结论:无论数组是否旋转,右端点(D)一定属于"右段单调子数组" (若未旋转,整个数组就是右段),且右段的所有元素都小于等于 右端点(因为右段单调递增),左段的所有元素都大于 右端点(因为左段>右段)。

例如:
- 旋转数组
[4,5,6,7,0,1,2]:右端点是2,右段[0,1,2]都 ≤ 2,左段[4,5,6,7]都 > 2; - 未旋转数组
[11,13,15,17]:右端点是17,整个数组(右段)都 ≤ 17,无左段。
基于这个结论,当我们计算中间值 nums[mid] 时,会出现两种情况:
1. nums[mid] < nums[right](中间值小于右端点)
结合下图,此时 nums[mid] 必然属于右段 (因为左段元素都大于右端点,不可能小于右端点)。由于右段单调递增,最小值一定在 mid 左侧(包括 mid 本身)------因为 mid 右侧的元素都 ≥ nums[mid],不可能是最小值。
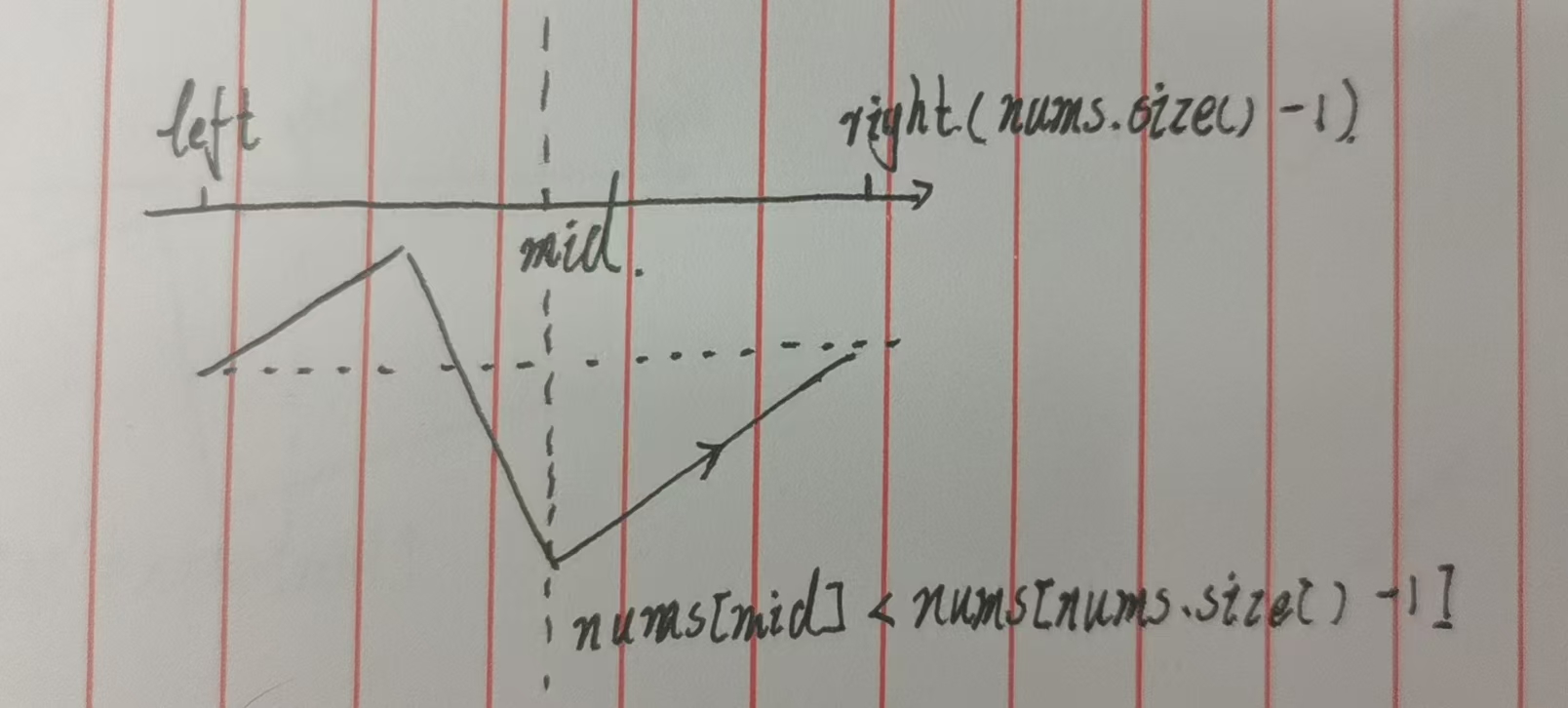
例如:nums = [4,5,6,7,0,1,2],right=6(值为2),若 mid=4(值为0),0 < 2,则最小值在 [0,4] 区间内(实际最小值就是 0)。
因此,我们需要舍弃右半部分,令 right = mid。
2. nums[mid] >= nums[right](中间值大于等于右端点)
结合下图,此时 nums[mid] 必然属于左段 (因为右段元素都 ≤ 右端点,不可能大于右端点)。由于左段单调递增且左段>右段,mid 及其左侧的元素都大于右段元素,最小值一定在 mid 右侧------mid 本身不可能是最小值。
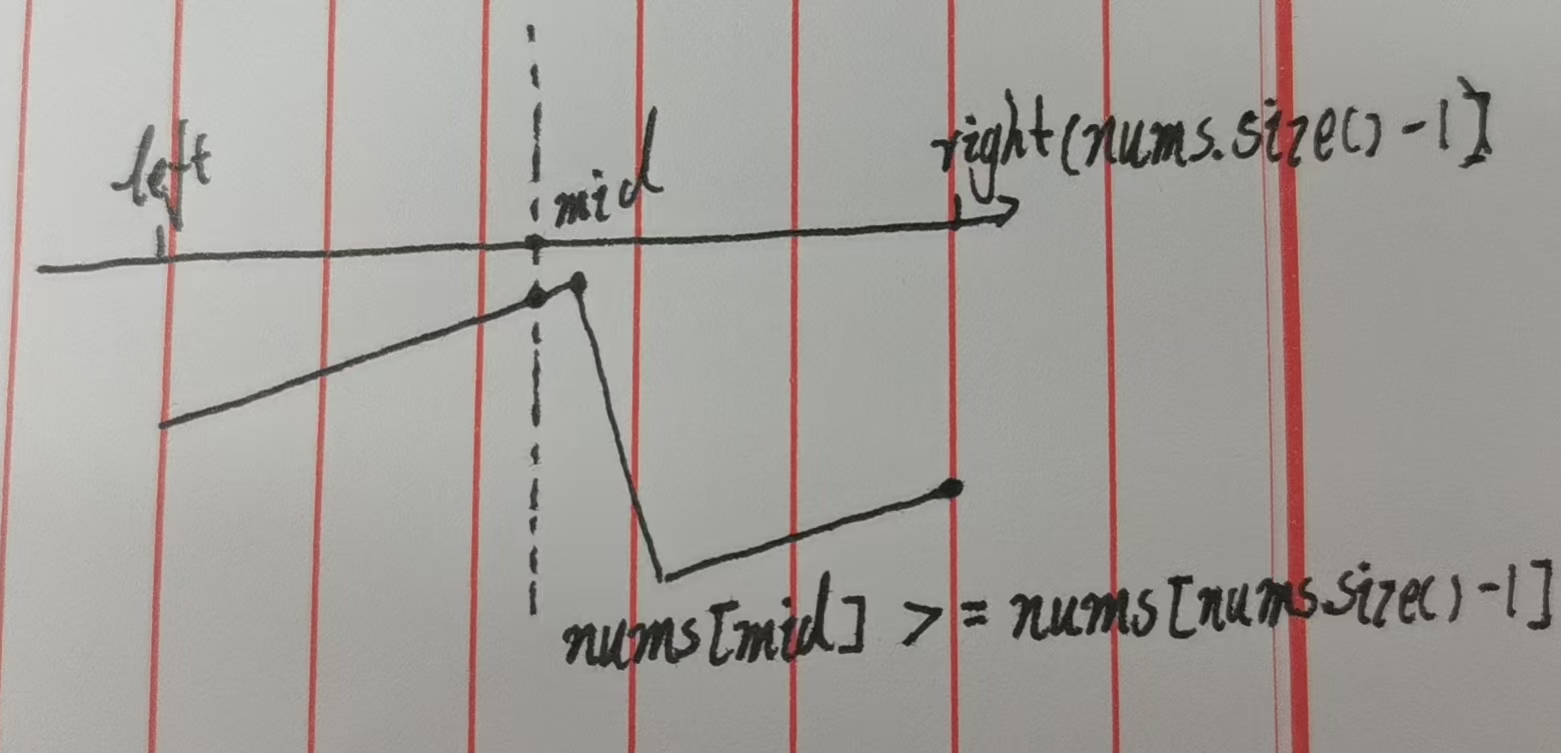
例如:nums = [4,5,6,7,0,1,2],right=6(值为2),若 mid=2(值为6),6 ≥ 2,则最小值在 [3,6] 区间内(排除了左段 [4,5,6])。
因此,我们需要舍弃左半部分,令 left = mid + 1。
代码实现
cpp
class Solution {
public:
int findMin(vector<int>& nums) {
int n = nums.size();
int left = 0, right = n - 1;
int x = nums[right]; // 提前存储右端点值,避免重复计算
while (left < right) { // 循环终止时 left == right,即为最小值下标
int mid = left + (right - left) / 2; // 避免溢出,等价于 (left+right)/2
if (nums[mid] < x) {
right = mid; // 舍弃右半部分,最小值在左侧
} else {
left = mid + 1; // 舍弃左半部分,最小值在右侧
}
}
return nums[left]; // 此时 left == right,返回对应值
}
};左端点(nums[0])
以左端点为基准的逻辑稍复杂,先明确结论:左端点一定属于"左段单调子数组" (若未旋转,整个数组就是左段),且左段的所有元素都大于等于 左端点(左段单调递增),右段的所有元素都小于 左端点(左段>右段)。

例如:
- 旋转数组
[4,5,6,7,0,1,2]:左端点是4,左段[4,5,6,7]都 ≥ 4,右段[0,1,2]都 < 4; - 未旋转数组
[11,13,15,17]:左端点是11,整个数组(左段)都 ≥ 11,无右段。
这里的关键问题是:未旋转数组会打破"左段>右段"的逻辑------此时数组整体递增,若仍按"左端点基准"判断,会出现错误。因此,以左端点为基准时,需要先处理"未旋转"的特殊情况。
接下来,在"已旋转"的前提下,计算中间值 nums[mid] 会出现两种情况,咱们将特殊情况放到最后说:
1. nums[0] > nums[mid](左端点大于中间值)
结合下图,此时 nums[mid] 必然属于右段 (因为左段元素都 ≤ 左端点,不可能小于左端点)。由于右段单调递增,最小值一定在 mid 左侧(包括 mid 本身)------因为 mid 右侧的元素都 ≥ nums[mid]。
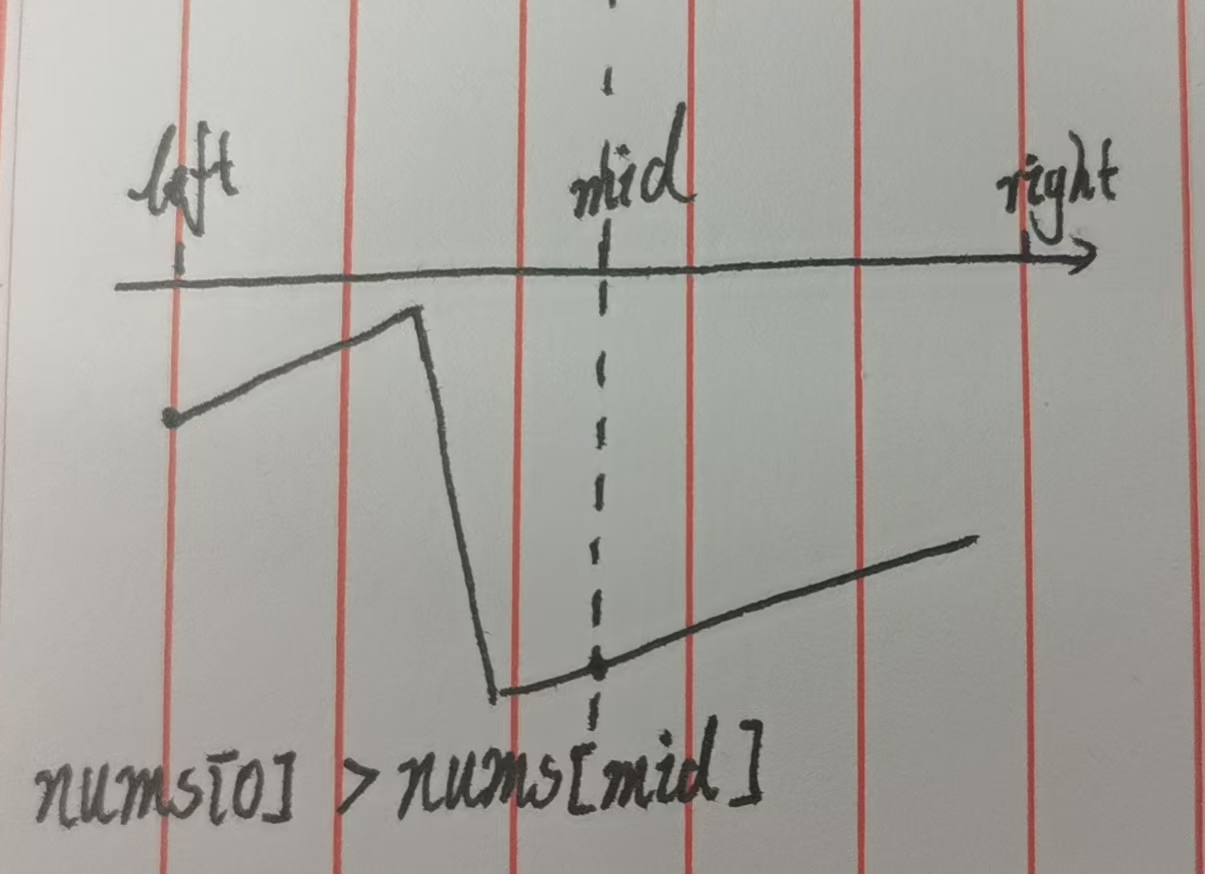
例如:nums = [4,5,6,7,0,1,2],nums[0] = 4,若 mid=4(值为0),4 > 0,则最小值在 [0,4] 区间内(实际最小值就是 0)。
因此,我们需要舍弃右半部分,令 right = mid。
2. nums[0] <= nums[mid](左端点小于等于中间值)
结合下图,此时 nums[mid] 必然属于左段 (因为右段元素都 < 左端点,不可能大于等于左端点)。由于左段单调递增且左段>右段,mid 及其左侧的元素都大于右段元素,最小值一定在 mid 右侧------mid 本身不可能是最小值。
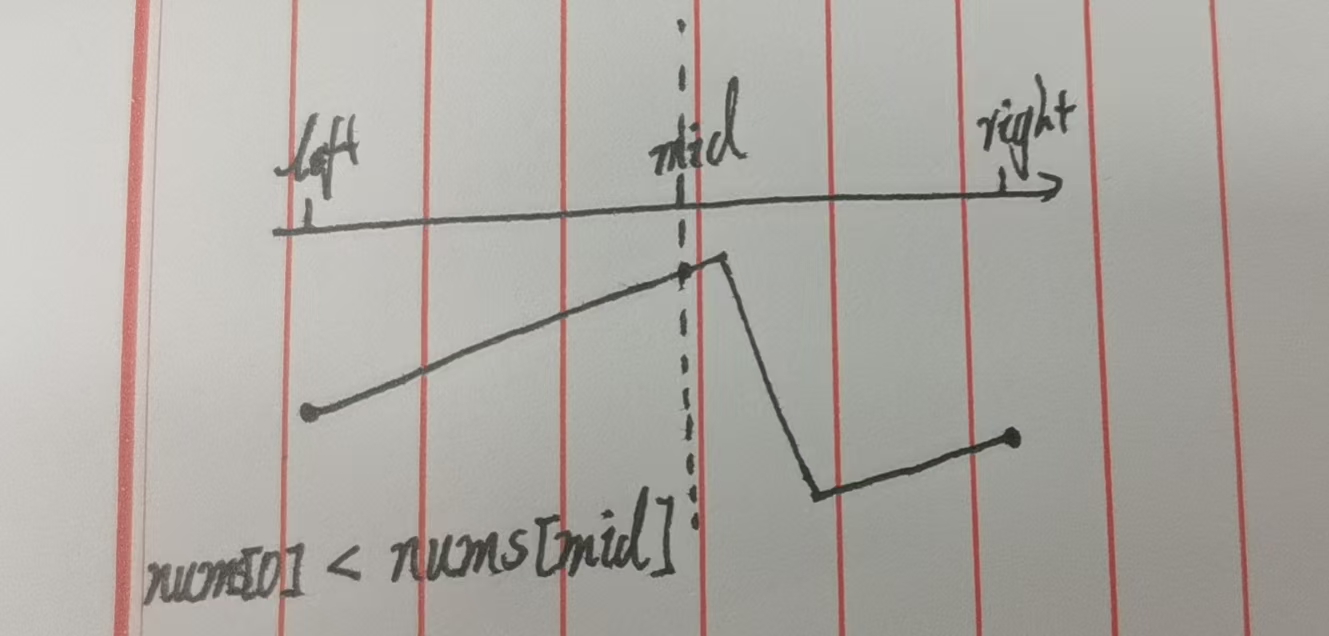
例如:nums = [4,5,6,7,0,1,2],nums[0] = 4,若 mid=2(值为6),4 ≤ 6,则最小值在 [3,6] 区间内(排除了左段 [4,5,6])。
因此,我们需要舍弃左半部分,令 left = mid + 1。
nums[0] <= nums[mid]的特殊情况处理
如前所述,若数组未旋转 (整体递增),例如 [11,13,15,17],此时 nums[0] = 11,无论 mid 取何值,nums[mid] 都 ≥ nums[0],会触发"left = mid + 1"的逻辑,导致 left 不断右移就(我的left要远航了...),最终错过最小值 11。
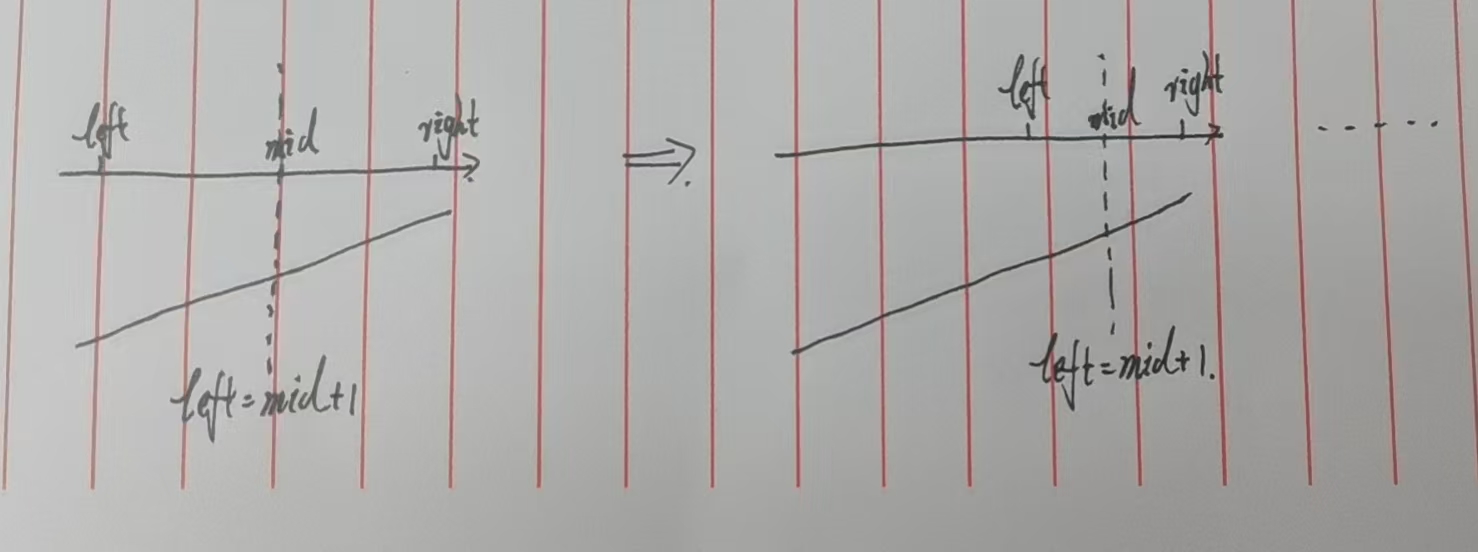
因此,以左端点为基准时,必须先判断数组是否未旋转 :若 nums[left] < nums[right](整体递增),直接返回 nums[left](即左端点,也是最小值)。
代码实现
cpp
class Solution {
public:
int findMin(vector<int>& nums) {
int n = nums.size();
int left = 0, right = n - 1;
// 特殊情况:数组未旋转(整体递增),直接返回左端点(最小值)
if (nums[left] < nums[right]) {
return nums[left];
}
int x = nums[left]; // 提前存储左端点值,避免重复计算
while (left < right) { // 循环终止时 left == right,即为最小值下标
int mid = left + (right - left) / 2; // 避免溢出
if (x > nums[mid]) {
right = mid; // 舍弃右半部分,最小值在左侧
} else {
left = mid + 1; // 舍弃左半部分,最小值在右侧
}
}
return nums[left]; // 此时 left == right,返回对应值
}
};细节总结
通过上面两种思路的对比,我们可以解答两个关键细节问题:
1. 为什么右端点不用判断是否为单调递增数组,左端点却要判断?
核心原因是两种基准的"特殊情况兼容性"不同:
- 对于右端点基准 :未旋转数组的"整体递增"可以被纳入"右段单调递增"的逻辑中------此时右段就是整个数组,
nums[mid] < nums[right]会始终成立,right会不断左移,最终left == right指向左端点(最小值),无需额外判断; - 对于左端点基准 :未旋转数组的"整体递增"会打破"左段>右段"的逻辑------此时无右段,
nums[0] <= nums[mid]始终成立,left会不断右移,最终指向右端点(最大值),导致错误。因此必须提前判断"整体递增"的情况。
2. x = nums[] 有必要一定写吗?
在我尝试这道题目的时候最开始没有用一个x来单独存储最左或最右侧的点,但是也能跑过所以我想在总结这里讨论下:写不写都能跑通的原因是 核心是因为数组端点值(nums[right] 或 nums[left])在整个二分过程中始终固定不变,重复访问也不会出错,只是用 x 存储能减少数组下标重复访问的开销、让代码更直观。
虽然不是"必须",但强烈建议写 ,原因有两点:
(1)提升代码可读性 :用 x 代表"基准端点值",循环内的 if (nums[mid] < x) 比 if (nums[mid] < nums[right]) 更直观,能让读者一眼看出"当前判断是基于基准值",降低理解成本。
(2)避免重复计算 :在循环中,nums[right] 或 nums[left] 的值不会变化(right 和 left 是下标,端点值固定),提前用 x 存储后,循环内只需访问 x,无需重复访问数组下标,减少操作开销;
下题预告
如果觉得这些内容对你有帮助,不妨点个赞支持一下,再关注我的博客。后续我还会持续分享更多算法干货,跟着系列文章一步步学,你对二分查找的掌握一定会越来越扎实~
下一篇博客我们将讨论力扣中的 LCR 173. 点名(本质是"在单调递增数组中找缺失元素",同样可以用二分查找高效解决,且会涉及新的二段性分析思路)。