leetcode
404. 左叶子之和 Sum of Left Leaves
题目
计算给定二叉树的所有左叶子之和。
Given the root of a binary tree, return the sum of all left leaves.
A leaf is a node with no children. A left leaf is a leaf that is the left child of another node.
示例:
3
/ \
9 20
/ \
15 7
在这个二叉树中,有两个左叶子,分别是 9 和 15,所以返回 24题解
前序遍历过程中添加记录左叶子节点的值。在递归过程中,我们使用一个标志位from_left来记录当前节点是否为上一层递归节点的左子节点。
Record the values of left leaf nodes during the preorder traversal. In the recursive process, we use a flag from_left to record whether the current node is the left child node of the recursive node in the upper level.
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
void dfs(TreeNode* root, bool from_left) {
if (!root) {
return;
}
bool is_leaf = !root->left && !root->right;
if (is_leaf && from_left) {
res += root->val;
return;
}
dfs(root->left, true);
dfs(root->right, false);
}
int sumOfLeftLeaves(TreeNode* root) {
bool from_left = false;
dfs(root, from_left);
return res;
}
private:
int res;
};
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def __init__(self):
self.res = 0
def sumOfLeftLeaves(self, root: Optional[TreeNode]) -> int:
self.core(root, False)
return self.res
def core(self, root, from_left):
if not root:
return
if from_left and root.left is None and root.right is None:
self.res += root.val
self.core(root.left, True)
self.core(root.right, False)
// 迭代版本
class Solution {
public:
bool is_leaf(TreeNode* root) {
if (!root) {
return false;
}
return !root->left && !root->right;
}
int sumOfLeftLeaves(TreeNode* root) {
if (!root) {
return 0;
}
queue<TreeNode*> q;
q.push(root);
int res = 0;
while (!q.empty()) {
auto node = q.front();
q.pop();
if (node->left) {
if (is_leaf(node->left)) {
res += node->left->val;
} else {
q.push(node->left);
}
}
if (node->right) {
if (!is_leaf(node->right)) {
q.push(node->right);
}
}
}
return res;
}
};复杂度
时间复杂度: O ( n ) O(n) O(n)
空间复杂度: O ( n ) O(n) O(n)
Time Complexity: O ( n ) O(n) O(n)
Space Complexity: O ( n ) O(n) O(n)
429. N-ary Tree Level Order Traversal
题目
Given an n-ary tree, return the level order traversal of its nodes' values.
Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples)
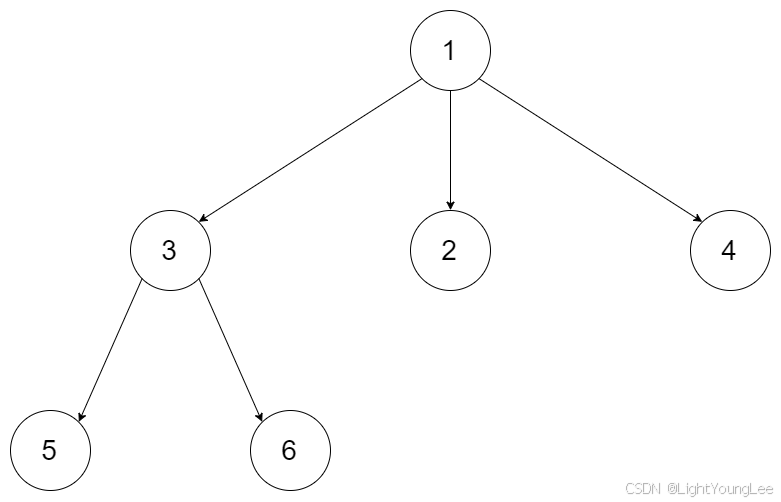
Input: root = [1,null,3,2,4,null,5,6]
Output: [[1],[3,2,4],[5,6]]
题解
正常层次遍历解决问题。
python
"""
# Definition for a Node.
class Node:
def __init__(self, val: Optional[int] = None, children: Optional[List['Node']] = None):
self.val = val
self.children = children
"""
import queue
class Solution:
def levelOrder(self, root: 'Node') -> List[List[int]]:
res = []
if not root:
return res
q = queue.Queue()
q.put(root)
while not q.empty():
length = q.qsize()
res_sub = []
for i in range(length):
node = q.get()
for child in node.children:
q.put(child)
res_sub.append(node.val)
res.append(res_sub)
return res复杂度
Time Complexity: O ( n ) O(n) O(n)
Space Complexity: O ( n ) O(n) O(n)
[hot] 437. 路径总和 III
题目
给定一个二叉树,它的每个结点都存放着一个整数值。
找出路径和等于给定数值的路径总数。
路径不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
二叉树不超过1000个节点,且节点数值范围是 [-1000000,1000000] 的整数。
Given the root of a binary tree and an integer targetSum, return the number of paths where the sum of the values along the path equals targetSum.
The path does not need to start or end at the root or a leaf, but it must go downwards (i.e., traveling only from parent nodes to child nodes).
示例:
root = [10,5,-3,3,2,null,11,3,-2,null,1], sum = 8
10
/ \
5 -3
/ \ \
3 2 11
/ \ \
3 -2 1
返回 3。和等于 8 的路径有:
1. 5 -> 3
2. 5 -> 2 -> 1
3. -3 -> 11题解
这个题明确提出路径前缀和以及hash_map组合解决问题。记录每条路径的累积和,如果发现当前累积和-target在之前出现过,那么之前的路径集合中一定存在==target的路径。
Solve the problem by combining prefix sum with a hash map. The hash map records the cumulative sum of each path; if it is found that the current cumulative sum minus the target has appeared before, then there must be a path equal to the target in the previous path set.
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int pathSum(TreeNode* root, int targetSum) {
m[0] = 1;
core(0, root, targetSum);
return res;
}
void core(long cur_sum, TreeNode* root, int targetSum) {
if (!root) {
return;
}
cur_sum += root->val;
if (m.find(cur_sum - targetSum) != m.end()) {
res += m[cur_sum - targetSum];
}
++m[cur_sum];
core(cur_sum, root->left, targetSum);
core(cur_sum, root->right, targetSum);
--m[cur_sum];
}
private:
// 可能会溢出,因而map的key被定义为long型
unordered_map<long, int> m;
int res = 0;
};
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
from collections import defaultdict
class Solution:
def __init__(self):
self.m = defaultdict(int)
self.res = 0
def pathSum(self, root: Optional[TreeNode], targetSum: int) -> int:
if not root:
return 0
self.m[0] = 1
self.core(0, root, targetSum)
return self.res
def core(self, cur_sum, root, targetSum):
if not root:
return
cur_sum += root.val
if self.m[cur_sum - targetSum] != 0:
self.res += self.m[cur_sum - targetSum]
self.m[cur_sum] += 1
self.core(cur_sum, root.left, targetSum)
self.core(cur_sum, root.right, targetSum)
self.m[cur_sum] -= 1
// [optional] 迭代
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int pathSum(TreeNode* root, int targetSum) {
if(root==NULL){
return 0;
}
unordered_map<long long,int>m;
stack<TreeNode*>s;
TreeNode*t=root;
TreeNode*last=NULL;
long long sum=t->val;
int count=0;
if(sum==targetSum){
count++;
}
m.insert({sum,1});
s.push(t);
if(root->val!=0){
m.insert({0,1});
}
else{
m[0]++;
}
while(!s.empty()){
if(t->left!=NULL&&(last==NULL||(last!=t->left&&last!=t->right))){
t=t->left;
sum+=t->val;
if(m.count(sum-targetSum)!=0){
count+=m[sum-targetSum];
}
if(m.count(sum)==0){
m.insert({sum,1});
}
else{
m[sum]++;
}
s.push(t);
continue;
}
if(t->right!=NULL&&last!=t->right){
t=t->right;
sum+=t->val;
if(m.count(sum-targetSum)!=0){
count+=m[sum-targetSum];
}
if(m.count(sum)==0){
m.insert({sum,1});
}
else{
m[sum]++;
}
s.push(t);
continue;
}
last=t;
m[sum]--;
sum-=t->val;
s.pop();
if(s.empty()){
break;
}
t=s.top();
}
return count;
}
};代码中m[0]=1的意义在于,能够正确记录从根节点开始,路径之和为targetSum的路径。case如下所示(targetSum = 22),如果没有该初始化操作,则5 -> 4 -> 11 -> 2和5 -> 8 -> 4 -> 5这两条路径就不会被正确记录下来。
The significance of setting m[0] = 1 in the code is that it enables the correct recording of paths starting from the root node where the sum of the path equals targetSum. For example, in the case where targetSum = 22, without this initialization, the two paths 5 -> 4 -> 11 -> 2 and 5 -> 8 -> 4 -> 5 would not be recorded correctly.

复杂度
时间复杂度: O ( n ) O(n) O(n),遍历一次树的时间
空间复杂度: O ( n ) O(n) O(n),最坏情况下树为一个单向链表,这时递归深度为树的节点个数
Time Complexity: O(n), which is the time required to traverse the tree once.
Space Complexity: O(n). In the worst case, the tree is a singly linked list, and the recursion depth is equal to the number of nodes in the tree.
450. 删除二叉搜索树中的节点 Delete Node in a BST
题目
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
首先找到需要删除的节点;
如果找到了,删除它。Given a root node reference of a BST and a key, delete the node with the given key in the BST. Return the root node reference (possibly updated) of the BST.
Basically, the deletion can be divided into two stages:
Search for a node to remove.
If the node is found, delete the node.
示例 1:
输入:root = [5,3,6,2,4,null,7], key = 3
输出:[5,4,6,2,null,null,7]
解释:给定需要删除的节点值是 3,所以我们首先找到 3 这个节点,然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。题解
二叉树递归解决问题。
- If the root value is larger than key, we need to do the recursion in left sub tree.
- and if the root value is less than key, we need to do the recursion in right sub tree.
- when the root value is equal to key, there are several cases to be handled:
- if the root is a leaf, return None
- if the root doesn't have left node, return root's right.
- if the root doesn't have right node, return root's left.
- the most complex case is that the root has both left and right node. We need to find the left-most node in root's right sub tree. Delete it and assign the value of this node to the root node.
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
if (!root) {
return nullptr;
}
if (root->val > key) {
root->left = deleteNode(root->left, key);
return root;
}
if (root->val < key) {
root->right = deleteNode(root->right, key);
return root;
}
if (!root->left && !root->right) {
return nullptr;
}
if (!root->left) {
return root->right;
}
if (!root->right) {
return root->left;
}
TreeNode* succ = root->right;
while (succ->left) {
succ = succ->left;
}
root->right = deleteNode(root->right, succ->val);
root->val = succ->val;
return root;
}
};
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def deleteNode(self, root: Optional[TreeNode], key: int) -> Optional[TreeNode]:
if not root:
return None
if root.val > key:
root.left = self.deleteNode(root.left, key)
return root
if root.val < key:
root.right = self.deleteNode(root.right, key)
return root
if not root.left and not root.right:
return None
if not root.left:
return root.right
if not root.right:
return root.left
succ = root.right
while succ.left:
succ = succ.left
root.right = self.deleteNode(root.right, succ.val)
root.val = succ.val
return root复杂度
时间复杂度: O ( n ) O(n) O(n)
空间复杂度: O ( n ) O(n) O(n)
Time Complexity: O ( n ) O(n) O(n)
Space Complexity: O ( n ) O(n) O(n)
[optional] 题解2
迭代实现上述过程,示例代码如下所示:
cpp
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
auto cur = root;
TreeNode* cur_p = nullptr;
while (cur && cur->val != key) {
cur_p = cur;
if (cur->val < key) {
cur = cur->right;
} else {
cur = cur->left;
}
}
// 处理待删除节点
if (!cur) {
return root;
}
if (!cur->left && !cur->right) {
cur = nullptr;
} else if (!cur->left) {
cur = cur->right;
} else if (!cur->right) {
cur = cur->left;
} else {
auto cur_succ = cur->right;
auto succ_p = cur;
while (cur_succ->left) {
succ_p = cur_succ;
cur_succ = cur_succ->left;
}
if (succ_p->val == cur->val) {
succ_p->right = cur_succ->right;
} else {
succ_p->left = cur_succ->right;
}
cur_succ->left = cur->left;
cur_succ->right = cur->right;
cur = cur_succ;
}
// 恢复待删除节点的上游连接情况
if (!cur_p) { // 待删除的节点就是root,或者根本就没有
return cur;
} else {
if (cur_p->left && cur_p->left->val == key) {
cur_p->left = cur;
} else {
cur_p->right = cur;
}
return root;
}
}
};复杂度
时间: O ( n ) O(n) O(n)
空间: O ( 1 ) O(1) O(1),无需借助额外的递归复杂度
513. 找树左下角的值 Find Bottom Left Tree Value
题目
给定一个二叉树的 根节点 root,请找出该二叉树的 最底层 最左边 节点的值。
假设二叉树中至少有一个节点。
Given the root of a binary tree, return the leftmost value in the last row of the tree.
示例 2:
输入: [1,2,3,4,null,5,6,null,null,7]
输出: 7
题解1
后序遍历,先遍历左子树,再遍历右子树,最左下方的节点肯定被优先遍历到。
Post-order traversal involves traversing the left subtree first, then the right subtree. The node at the bottom-leftmost position is definitely traversed first.
cpp
class Solution {
public:
void dfs(TreeNode* root, int height, int& curVal, int& curHeight) {
if (!root) {
return;
}
++height;
dfs(root->left, height, curVal, curHeight);
dfs(root->right, height, curVal, curHeight);
if (height > curHeight) {
curHeight = height;
curVal = root->val;
}
}
int findBottomLeftValue(TreeNode* root) {
int curVal = 0, curHeight = 0;
dfs(root, 0, curVal, curHeight);
return curVal;
}
};
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
import queue
class Solution:
def __init__(self):
self.cur_val = 0
self.cur_height = 0
def findBottomLeftValue(self, root: Optional[TreeNode]) -> int:
if not root:
return None
self.core(root, 0)
return self.cur_val
def core(self, root, height):
if not root:
return
height += 1
self.core(root.left, height)
self.core(root.right, height)
if height > self.cur_height:
self.cur_height = height
self.cur_val = root.val
return 复杂度
时间: O ( n ) O(n) O(n)
空间: O ( n ) O(n) O(n)
Time Complexity: O ( n ) O(n) O(n)
Space Complexity: O ( n ) O(n) O(n)
题解2
迭代法层次遍历,每层第一次pop元素时更新res,遍历完成后res即为最终结果。
Perform level order traversal using the iterative method. Update the res variable when popping the first element of each level, and res will be the final result after the traversal is completed.
cpp
class Solution {
public:
int findBottomLeftValue(TreeNode* root) {
queue<TreeNode*> q;
q.push(root);
int ret = 0;
while (!q.empty()) {
auto p = q.front();
q.pop();
if (p->right) {
q.push(p->right);
}
if (p->left) {
q.push(p->left);
}
ret = p->val;
}
return ret;
}
};
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
import queue
class Solution:
def findBottomLeftValue(self, root: Optional[TreeNode]) -> int:
if not root:
return None
q = queue.Queue()
q.put(root)
res = root.val
while not q.empty():
length = q.qsize()
for i in range(length):
node = q.get()
if node.left:
q.put(node.left)
if node.right:
q.put(node.right)
if i == 0:
res = node.val
return res复杂度
时间: O ( n ) O(n) O(n)
空间: O ( n ) O(n) O(n)
Time Complexity: O ( n ) O(n) O(n)
Space Complexity: O ( n ) O(n) O(n)
530. Minimum Absolute Difference in BST
题目
Given the root of a Binary Search Tree (BST), return the minimum absolute difference between the values of any two different nodes in the tree.
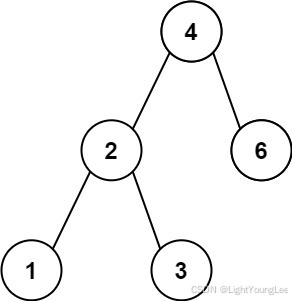
题解
中序遍历解决问题。
python
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def getMinimumDifference(self, root: Optional[TreeNode]) -> int:
last_val = -1
min_diff = 1000000
stk = []
while root or len(stk) > 0:
while root:
stk.append(root)
root = root.left
node = stk.pop()
root = node.right
if last_val != -1 and node.val - last_val < min_diff:
min_diff = node.val - last_val
last_val = node.val
return min_diff复杂度
Time Complexity: O ( n ) O(n) O(n)
Space Complexity: O ( n ) O(n) O(n)
536. Construct Binary Tree from String
题目
You need to construct a binary tree from a string consisting of parenthesis and integers.
The whole input represents a binary tree. It contains an integer followed by zero, one or two pairs of parenthesis. The integer represents the root's value and a pair of parenthesis contains a child binary tree with the same structure.
You always start to construct the left child node of the parent first if it exists.
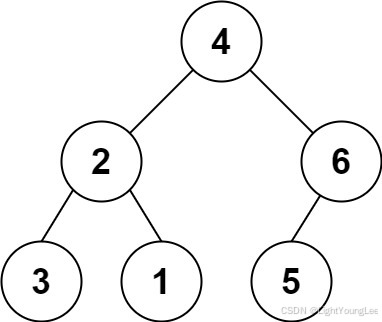
Input: s = "4(2(3)(1))(6(5))"
Output: [4,2,6,3,1,5]
题解
dfs + 栈 解决问题。
python
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def gen_node(self, num, stk):
node = TreeNode(int(num)) if num else None
if stk:
if not stk[-1].left:
stk[-1].left = node
elif not stk[-1].right:
stk[-1].right = node
if node:
stk.append(node)
return ''
def str2tree(self, s: str) -> Optional[TreeNode]:
num, stk = '', []
for i in s:
if i == '(':
num = self.gen_node(num, stk)
elif i == ')':
num = self.gen_node(num, stk)
stk.pop()
else:
num += i
return stk[-1] if stk else None if not s else TreeNode(int(s))复杂度
Time Complexity: O ( n ) O(n) O(n)
Space Complexity: O ( n ) O(n) O(n)
[hot] 538. 把二叉搜索树转换为累加树 Convert BST to Greater Tree
题目
给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
提醒一下,二叉搜索树满足下列约束条件:
节点的左子树仅包含键 小于 节点键的节点。
节点的右子树仅包含键 大于 节点键的节点。
左右子树也必须是二叉搜索树。Given the root of a Binary Search Tree (BST), convert it to a Greater Tree such that every key of the original BST is changed to the original key plus the sum of all keys greater than the original key in BST.
As a reminder, a binary search tree is a tree that satisfies these constraints:
- The left subtree of a node contains only nodes with keys less than the node's key.
- The right subtree of a node contains only nodes with keys greater than the node's key.
- Both the left and right subtrees must also be binary search trees.

示例 1:
输入:[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出:[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
示例 2:
输入:root = [0,null,1]
输出:[1,null,1]
示例 3:
输入:root = [1,0,2]
输出:[3,3,2]
示例 4:
输入:root = [3,2,4,1]
输出:[7,9,4,10]题解
反序二叉树中序遍历解决问题。
Solving problems with reverse in-order traversal of a binary tree.
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* convertBST(TreeNode* root) {
if (root) {
convertBST(root->right);
sum += root->val;
root->val = sum;
convertBST(root->left);
}
return root;
}
private:
int sum = 0;
};
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def __init__(self):
self.cur_res = 0
def core(self, root):
if not root:
return
self.core(root.right)
self.cur_res += root.val
root.val = self.cur_res
self.core(root.left)
def convertBST(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
self.core(root)
return root
// 递归 反向中序遍历
class Solution {
public:
TreeNode* convertBST(TreeNode* root) {
int sum = 0;
stack<TreeNode*> stk;
auto cur = root;
while (!stk.empty() || cur) {
while (cur) {
stk.push(cur);
cur = cur->right;
}
if (!stk.empty()) {
auto node = stk.top();
stk.pop();
sum += node->val;
node->val = sum;
cur = node->left;
}
}
return root;
}
};复杂度
时间复杂度: O ( n ) O(n) O(n)
空间复杂度: O ( n ) O(n) O(n)
Time Complexity: O ( n ) O(n) O(n)
Space Complexity: O ( n ) O(n) O(n)
543. 二叉树的直径 Diameter of Binary Tree
题目
给定一棵二叉树,你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。
注意:两结点之间的路径长度是以它们之间边的数目表示。
Given the root of a binary tree, return the length of the diameter of the tree.
The diameter of a binary tree is the length of the longest path between any two nodes in a tree. This path may or may not pass through the root.
The length of a path between two nodes is represented by the number of edges between them.
示例 :
给定二叉树
1
/ \
2 3
/ \
4 5
返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。题解
通过dfs来记录以root为终止节点的最长路径对应的节点数。执行如下两步:
- 通过递归来记录以左右子节点为终止节点的最大节点数l和r。
- 1 + l + r的最大值即为最终结果。
Use DFS to record the number of nodes corresponding to the longest path ending at the root node. Execute the following two steps:
- Use recursion to record the maximum number of nodes l and r for the longest paths ending at the left and right child nodes respectively.
- The maximum value of 1 + l + r will be the final result.
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int diameterOfBinaryTree(TreeNode* root) {
dfs(root);
// 目标是边的最大值,即最大节点数 - 1
return ans - 1;
}
int dfs(TreeNode* root) {
if (!root) {
return 0;
}
int max_left = dfs(root->left);
int max_right = dfs(root->right);
ans = max(ans, max_left + max_right + 1);
return 1 + max(max_left, max_right);
}
private:
int ans = 1;
};
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def __init__(self):
self.res = 0
def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:
if not root:
return 0
self.core(root)
return self.res - 1
def core(self, root):
if not root:
return 0
left_path = self.core(root.left)
right_path = self.core(root.right)
self.res = max(self.res, 1 + left_path + right_path)
return 1 + max(left_path, right_path)复杂度
时间复杂度: O ( n ) O(n) O(n)
空间复杂度: O ( n ) O(n) O(n)
Time Complexity: O ( n ) O(n) O(n)
Space Complexity: O ( n ) O(n) O(n)
题解2
迭代法解决问题,示例代码如下:
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
// 时间复杂度为O(n),空间复杂度为O(n),且比递归法的辅助空间开的更多
class Solution {
public:
int diameterOfBinaryTree(TreeNode* root) {
if (!root) {
return 0;
}
unordered_map<TreeNode*, int> m;
int res = -1;
// 给map赋默认值非常重要,这决定了后续遍历会不会死循环
m[nullptr] = 0;
stack<TreeNode*> stk;
stk.push(root);
while (!stk.empty()) {
auto node = stk.top();
stk.pop();
if (m.count(node->left) && m.count(node->right)) {
m[node] = max(m[node->left], m[node->right]) + 1;
res = max(res, m[node->left] + m[node->right]);
} else {
// 保存现场很重要
stk.push(node);
if (node->right) {
stk.push(node->right);
}
if (node->left) {
stk.push(node->left);
}
}
}
return res;
}
};545. Boundary of Binary Tree
题目
The boundary of a binary tree is the concatenation of the root, the left boundary, the leaves ordered from left-to-right, and the reverse order of the right boundary.
The left boundary is the set of nodes defined by the following:
The root node's left child is in the left boundary. If the root does not have a left child, then the left boundary is empty.
If a node is in the left boundary and has a left child, then the left child is in the left boundary.
If a node is in the left boundary, has no left child, but has a right child, then the right child is in the left boundary.
The leftmost leaf is not in the left boundary.The right boundary is similar to the left boundary, except it is the right side of the root's right subtree. Again, the leaf is not part of the right boundary, and the right boundary is empty if the root does not have a right child.
The leaves are nodes that do not have any children. For this problem, the root is not a leaf.
Given the root of a binary tree, return the values of its boundary.
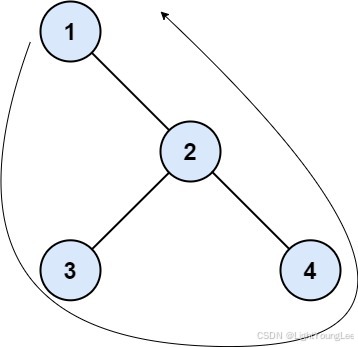
Input: root = [1,null,2,3,4]
Output: [1,3,4,2]
Explanation:
- The left boundary is empty because the root does not have a left child.
- The right boundary follows the path starting from the root's right child 2 -> 4.
4 is a leaf, so the right boundary is [2]. - The leaves from left to right are [3,4].
Concatenating everything results in [1] + [] + [3,4] + [2] = [1,3,4,2].
题解
分 左边界、叶子结点、右边界 来解决问题。
python
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def __init__(self):
self.res = []
def is_leaf(self, root):
return not root.left and not root.right
def get_leaf(self, root):
if not root:
return
if not root.left and not root.right:
self.res.append(root.val)
self.get_leaf(root.left)
self.get_leaf(root.right)
def boundaryOfBinaryTree(self, root: Optional[TreeNode]) -> List[int]:
if not root:
return []
self.res.append(root.val)
if self.is_leaf(root):
return self.res
node = root.left
while node and not self.is_leaf(node):
self.res.append(node.val)
if node.left:
node = node.left
else:
node = node.right
self.get_leaf(root)
node = root.right
stk = []
while node and not self.is_leaf(node):
stk.append(node.val)
if node.right:
node = node.right
else:
node = node.left
while len(stk) > 0:
self.res.append(stk.pop())
return self.res复杂度
Time Complexity: O ( n ) O(n) O(n)
Space Complexity: O ( n ) O(n) O(n)
[hot] 617. 合并二叉树 Merge Two Binary Trees
题目
给定两个二叉树,想象当你将它们中的一个覆盖到另一个上时,两个二叉树的一些节点便会重叠。
你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠,那么将他们的值相加作为节点合并后的新值,否则不为 NULL 的节点将直接作为新二叉树的节点。
示例 1:
输入:
Tree 1 Tree 2
1 2
/ \ / \
3 2 1 3
/ \ \
5 4 7
输出:
合并后的树:
3
/ \
4 5
/ \ \
5 4 7题解
这个题和<合并两个有序数组>思路类似,深度优先遍历解决问题。
This problem is similar in thinking to "Merge Two Sorted Arrays" and can be solved using Depth-First Search (DFS).
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
if (!root1) {
return root2;
}
if (!root2) {
return root1;
}
TreeNode* root = new TreeNode(root1->val + root2->val);
root->left = mergeTrees(root1->left, root2->left);
root->right = mergeTrees(root1->right, root2->right);
return root;
}
};
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def mergeTrees(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> Optional[TreeNode]:
if not root1:
return root2
if not root2:
return root1
node = TreeNode(root1.val + root2.val)
node.left = self.mergeTrees(root1.left, root2.left)
node.right = self.mergeTrees(root1.right, root2.right)
return node
// 迭代形式
class Solution {
public:
TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
if (t1 == nullptr) {
return t2;
}
if (t2 == nullptr) {
return t1;
}
auto merged = new TreeNode(t1->val + t2->val);
auto q = queue<TreeNode*>();
auto queue1 = queue<TreeNode*>();
auto queue2 = queue<TreeNode*>();
q.push(merged);
queue1.push(t1);
queue2.push(t2);
while (!queue1.empty() && !queue2.empty()) {
auto node = q.front(), node1 = queue1.front(), node2 = queue2.front();
q.pop();
queue1.pop();
queue2.pop();
auto left1 = node1->left, left2 = node2->left, right1 = node1->right, right2 = node2->right;
if (left1 != nullptr || left2 != nullptr) {
if (left1 != nullptr && left2 != nullptr) {
auto left = new TreeNode(left1->val + left2->val);
node->left = left;
q.push(left);
queue1.push(left1);
queue2.push(left2);
} else if (left1 != nullptr) {
node->left = left1;
} else if (left2 != nullptr) {
node->left = left2;
}
}
if (right1 != nullptr || right2 != nullptr) {
if (right1 != nullptr && right2 != nullptr) {
auto right = new TreeNode(right1->val + right2->val);
node->right = right;
q.push(right);
queue1.push(right1);
queue2.push(right2);
} else if (right1 != nullptr) {
node->right = right1;
} else {
node->right = right2;
}
}
}
return merged;
}
};
// Python Version
from collections import deque
class Solution:
def mergeTrees(self, t1: TreeNode, t2: TreeNode) -> TreeNode:
# 边界条件:如果其中一棵树为空,直接返回另一棵树
if not t1:
return t2
if not t2:
return t1
# 创建合并后的根节点,值为两棵树根节点值的和
merged = TreeNode(t1.val + t2.val)
# Python中用deque实现队列(效率远高于list,替代C++的queue)
q = deque()
queue1 = deque()
queue2 = deque()
# 初始化队列,存入根节点
q.append(merged)
queue1.append(t1)
queue2.append(t2)
# 循环处理队列中的节点,直到其中一个队列为空
while queue1 and queue2:
# 取出队列头部节点(C++的front() + pop())
node = q.popleft()
node1 = queue1.popleft()
node2 = queue2.popleft()
# 获取左右子节点
left1, left2 = node1.left, node2.left
right1, right2 = node1.right, node2.right
# 处理左子树
if left1 or left2: # 至少有一个左子节点存在
if left1 and left2: # 两个左子节点都存在,创建新节点
left_node = TreeNode(left1.val + left2.val)
node.left = left_node
q.append(left_node)
queue1.append(left1)
queue2.append(left2)
elif left1: # 只有t1的左子节点存在
node.left = left1
else: # 只有t2的左子节点存在
node.left = left2
# 处理右子树(逻辑和左子树完全一致)
if right1 or right2:
if right1 and right2:
right_node = TreeNode(right1.val + right2.val)
node.right = right_node
q.append(right_node)
queue1.append(right1)
queue2.append(right2)
elif right1:
node.right = right1
else:
node.right = right2
return merged
复杂度
时间复杂度: O ( m i n ( m , n ) ) O(min(m, n)) O(min(m,n)),m和n代表两棵树的节点数
空间复杂度: O ( m i n ( m , n ) ) O(min(m, n)) O(min(m,n))
Time complexity: O(min(m,n)), where m and n represent the number of nodes in the two trees.
Space complexity: O(min(m,n))
687. Longest Univalue Path
题目
Given the root of a binary tree, return the length of the longest path, where each node in the path has the same value. This path may or may not pass through the root.
The length of the path between two nodes is represented by the number of edges between them.
Example 1:
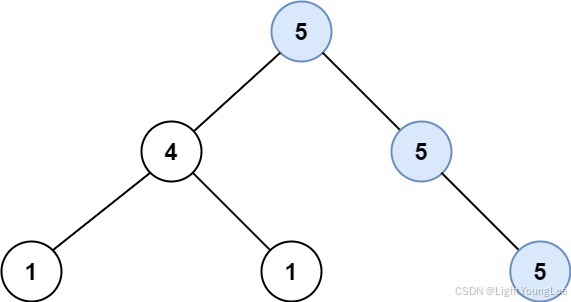
Input: root = [5,4,5,1,1,null,5]
Output: 2
Explanation: The shown image shows that the longest path of the same value (i.e. 5).
题解
类似计算二叉树的直径。
python
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def __init__(self):
self.res = 0
def longestUnivaluePath(self, root: Optional[TreeNode]) -> int:
self.core(root)
return self.res
def core(self, root):
if not root:
return 0
left = self.core(root.left)
right = self.core(root.right)
left = left + 1 if root.left and root.left.val == root.val else 0
right = right + 1 if root.right and root.right.val == root.val else 0
self.res = max(self.res, left + right)
return max(left, right)复杂度
Time Complexity: O ( n ) O(n) O(n)
Space Complexity: O ( n ) O(n) O(n)
700. 二叉搜索树中的搜索 Search in a Binary Search Tree
题目
给定二叉搜索树(BST)的根节点 root 和一个整数值 val。
你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在,则返回 null 。
You are given the root of a binary search tree (BST) and an integer val.
Find the node in the BST that the node's value equals val and return the subtree rooted with that node. If such a node does not exist, return null.
题解
二分遍历解决问题。
The problem is solved using binary traversal.
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* searchBST(TreeNode* root, int val) {
auto cur = root;
while (cur && cur->val != val) {
if (cur->val < val) {
cur = cur->right;
} else {
cur = cur->left;
}
}
return cur;
}
};
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def searchBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
if not root:
return None
while root and root.val != val:
if root.val > val:
root = root.left
elif root.val < val:
root = root.right
return root
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def searchBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
if not root:
return None
stk = []
while root or len(stk) > 0:
while root:
stk.append(root)
root = root.left
if len(stk) > 0:
node = stk.pop()
if node.val == val:
return node
root = node.right
return None
// 递归形式
class Solution {
public:
TreeNode* searchBST(TreeNode* root, int val) {
if (!root) {
return nullptr;
}
if (root->val == val) {
return root;
}
return searchBST(val < root->val ? root->left : root->right, val);
}
};复杂度
时间: O ( l o g n ) O(logn) O(logn)
空间: O ( 1 ) O(1) O(1)
Time Complexity: O ( l o g n ) O(logn) O(logn)
Space Complexity: O ( 1 ) O(1) O(1)
701. 二叉搜索树中的插入操作 Insert into a Binary Search Tree
题目
给定二叉搜索树(BST)的根节点 root 和要插入树中的值 value ,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ,新值和原始二叉搜索树中的任意节点值都不同。
注意,可能存在多种有效的插入方式,只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。
You are given the root node of a binary search tree (BST) and a value to insert into the tree. Return the root node of the BST after the insertion. It is guaranteed that the new value does not exist in the original BST.
Notice that there may exist multiple valid ways for the insertion, as long as the tree remains a BST after insertion. You can return any of them.
题解
直接找到合适的空位,插入节点即可。
Just find a suitable empty position and insert the node directly.
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* insertIntoBST(TreeNode* root, int val) {
if (!root) {
return new TreeNode(val);
}
auto p = root;
while (p) {
if (p->val < val) {
if (p->right == nullptr) {
p->right = new TreeNode(val);
break;
} else {
p = p->right;
}
} else {
if (p->left == nullptr) {
p->left = new TreeNode(val);
break;
} else {
p = p->left;
}
}
}
return root;
}
};
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def insertIntoBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
if not root:
return TreeNode(val)
p = root
while p:
if p.val < val:
if not p.right:
p.right = TreeNode(val)
break
else:
p = p.right
elif p.val > val:
if not p.left:
p.left = TreeNode(val)
break
else:
p = p.left
return root
// 递归方法
class Solution {
public:
TreeNode* insertIntoBST(TreeNode* root, int val) {
if (!root) {
return new TreeNode(val);
}
if (root->val > val) {
root->left = insertIntoBST(root->left, val);
} else {
root->right = insertIntoBST(root->right, val);
}
return root;
}
};
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def insertIntoBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
if not root:
return TreeNode(val)
if root.val > val:
root.left = self.insertIntoBST(root.left, val)
elif root.val < val:
root.right = self.insertIntoBST(root.right, val)
return root复杂度
Iteration Version:
时间: O ( n ) O(n) O(n)
空间: O ( 1 ) O(1) O(1)
Time Complexity: O ( n ) O(n) O(n)
Space Complexity: O ( 1 ) O(1) O(1)
Recursion Version:
Time Complexity: O ( n ) O(n) O(n)
Space Complexity: O ( n ) O(n) O(n)
783. 二叉搜索树节点最小距离 Minimum Distance Between BST Nodes
题目
给你一个二叉搜索树的根节点 root ,返回 树中任意两不同节点值之间的最小差值 。
Given the root of a Binary Search Tree (BST), return the minimum difference between the values of any two different nodes in the tree.
题解
中序遍历过程中记录最小差值。
Record the minimum difference during in-order traversal.
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int minDiffInBST(TreeNode* root) {
int res = INT_MAX;
stack<TreeNode*> stk;
bool flag = false;
int last = 0;
while (root || !stk.empty()) {
while (root) {
stk.push(root);
root = root->left;
}
if (!stk.empty()) {
TreeNode* node = stk.top();
stk.pop();
if (flag && node->val - last < res) {
res = node->val - last;
}
root = node->right;
last = node->val;
flag = true;
}
}
return res;
}
};
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def minDiffInBST(self, root: Optional[TreeNode]) -> int:
flag = False
last_value = -1
res = 1000000
stk = []
while root or len(stk) > 0:
while root:
stk.append(root)
root = root.left
if len(stk) > 0:
node = stk.pop()
if flag:
res = min(res, node.val - last_value)
root = node.right
flag = True
last_value = node.val
return res
// 递归形式
class Solution {
public:
void dfs(TreeNode* root, int& pre, int& ans) {
if (root == nullptr) {
return;
}
dfs(root->left, pre, ans);
if (pre != -1) {
ans = min(ans, root->val - pre);
}
pre = root->val;
dfs(root->right, pre, ans);
}
int minDiffInBST(TreeNode* root) {
int ans = INT_MAX, pre = -1;
dfs(root, pre, ans);
return ans;
}
};复杂度
时间复杂度: O ( n ) O(n) O(n)
空间复杂度: O ( n ) O(n) O(n),有额外的栈空间
Time Complexity: O ( n ) O(n) O(n)
Space Complexity: O ( n ) O(n) O(n), addtional space of the stack
863. All Nodes Distance K in Binary Tree
题目
Given the root of a binary tree, the value of a target node target, and an integer k, return an array of the values of all nodes that have a distance k from the target node.
You can return the answer in any order.
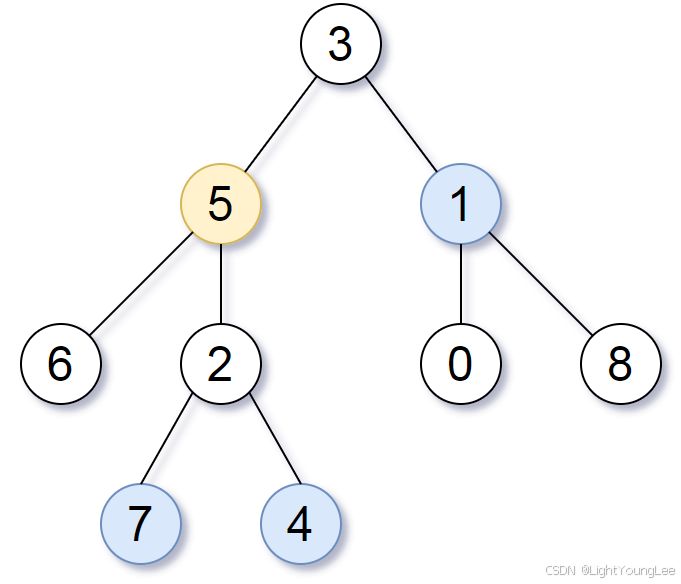
Input: root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, k = 2
Output: [7,4,1]
Explanation: The nodes that are a distance 2 from the target node (with value 5) have values 7, 4, and 1.
题解
先找到每个节点的parent,然后再通过左、右、parent的顺序,来找到指定节点集合。
python
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def __init__(self):
self.parents = {}
self.res = []
def find_parents(self, root):
if root.left:
self.parents[root.left.val] = root
self.find_parents(root.left)
if root.right:
self.parents[root.right.val] = root
self.find_parents(root.right)
def find_res(self, node, from_t, depth, k):
if not node:
return
if depth == k:
self.res.append(node.val)
return
if node.left != from_t:
self.find_res(node.left, node, depth + 1, k)
if node.right != from_t:
self.find_res(node.right, node, depth + 1, k)
# root doesn't have parents
if node.val in self.parents and self.parents[node.val] != from_t:
self.find_res(self.parents[node.val], node, depth + 1, k)
def distanceK(self, root: TreeNode, target: TreeNode, k: int) -> List[int]:
self.find_parents(root)
self.find_res(target, None, 0, k)
return self.res复杂度
Time Complexity: O ( n ) O(n) O(n)
Space Complexity: O ( n ) O(n) O(n)
938. Range Sum of BST
题目
Given the root node of a binary search tree and two integers low and high, return the sum of values of all nodes with a value in the inclusive range [low, high].
题解
中序遍历解决问题。
python
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def __init__(self):
self.res = 0
def rangeSumBST(self, root: Optional[TreeNode], low: int, high: int) -> int:
self.core(root, low, high)
return self.res
def core(self, root, low, high):
if not root:
return
if low <= root.val <= high:
self.res += root.val
self.core(root.left, low, high)
self.core(root.right, low, high)复杂度
Time Complexity: O ( n ) O(n) O(n)
Space Complexity: O ( n ) O(n) O(n)
958. Check Completeness of a Binary Tree
题目
Given the root of a binary tree, determine if it is a complete binary tree.
In a complete binary tree, every level, except possibly the last, is completely filled, and all nodes in the last level are as far left as possible. It can have between 1 and 2h nodes inclusive at the last level h.
题解
层次遍历解决问题,碰到过空节点之后就不能再有空节点了。
python
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
import queue
class Solution:
def isCompleteTree(self, root: Optional[TreeNode]) -> bool:
if not root:
return True
q = queue.Queue()
q.put(root)
seen_null = False
while not q.empty():
node = q.get()
if not node:
seen_null = True
elif not seen_null:
q.put(node.left)
q.put(node.right)
else:
return False
return True复杂度
Time Complexity: O ( n ) O(n) O(n)
Space Complexity: O ( n ) O(n) O(n)
[optional] 1377. Frog Position After T Seconds
[optional] 1443. Minimum Time to Collect All Apples in a Tree
题目
Given an undirected tree consisting of n vertices numbered from 0 to n-1, which has some apples in their vertices. You spend 1 second to walk over one edge of the tree. Return the minimum time in seconds you have to spend to collect all apples in the tree, starting at vertex 0 and coming back to this vertex.
The edges of the undirected tree are given in the array edges, where edges[i] = [ai, bi] means that exists an edge connecting the vertices ai and bi. Additionally, there is a boolean array hasApple, where hasApple[i] = true means that vertex i has an apple; otherwise, it does not have any apple.
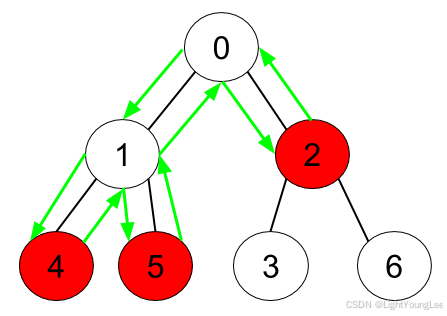
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,true,true,false]
Output: 8
Explanation: The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.
题解
python
class Solution:
def minTime(self, n: int, edges: List[List[int]], hasApple: List[bool]) -> int:
# 建树
g = [[] for _ in range(n)]
for x, y in edges:
g[x].append(y)
g[y].append(x)
# 自底向上
def dfs(x, fa):
cost = 0
for y in g[x]:
# 避免死循环
if y == fa:
continue
y_cost = dfs(y, x)
# 以节点 y 为根的子树包含苹果,则必须经过节点 y
if y_cost or hasApple[y]:
# 拓展新子节点的时候走一次,回溯的时候再走一次
# 所以边 x-y 要经过两次
cost += y_cost + 2
return cost
return dfs(0, -1)复杂度
Time Complexity: O ( n ) O(n) O(n)
Space Complexity: O ( n ) O(n) O(n)
1485.Clone Binary Tree With Random Pointer
题目
A binary tree is given such that each node contains an additional random pointer which could point to any node in the tree or null.
Return a deep copy of the tree.
The tree is represented in the same input/output way as normal binary trees where each node is represented as a pair of [val, random_index] where:
val: an integer representing Node.val
random_index: the index of the node (in the input) where the random pointer points to, or null if it does not point to any node.You will be given the tree in class Node and you should return the cloned tree in class NodeCopy. NodeCopy class is just a clone of Node class with the same attributes and constructors.
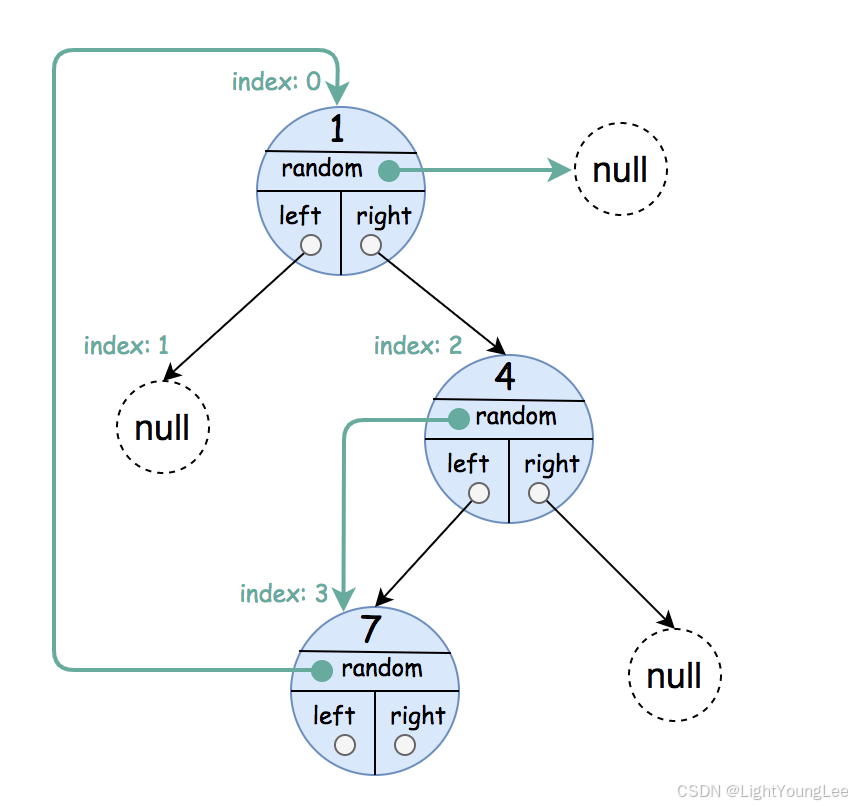
Input: root = [[1,null],null,[4,3],[7,0]]
Output: [[1,null],null,[4,3],[7,0]]
Explanation: The original binary tree is [1,null,4,7].
The random pointer of node one is null, so it is represented as [1, null].
The random pointer of node 4 is node 7, so it is represented as [4, 3] where 3 is the index of node 7 in the array representing the tree.
The random pointer of node 7 is node 1, so it is represented as [7, 0] where 0 is the index of node 1 in the array representing the tree.
题解
遍历过程中fork,但需要记得重新构建random节点。
python
# Definition for a binary tree node.
# class Node:
# def __init__(self, val=0, left=None, right=None, random=None):
# self.val = val
# self.left = left
# self.right = right
# self.random = random
class Solution:
def copyRandomBinaryTree(self, root: 'Node') -> 'NodeCopy':
d={}
#沿着树dfs 一定能遍历整颗原树,而后d 这个字典 k 是原树节点,v 是新树对应的节点,
def dfs(r):
if not r:
return
new = NodeCopy(r.val)
new.left = dfs(r.left)
new.right = dfs(r.right)
new.random=None
d[r] = new
return new
# 先把左右树都建立好了,字典也建立好。
#这个题,最难的是,题意,其实,就是root.random 也是指向一棵树,不要管索引index
t = dfs(root)
for k,v in d.items():
#因为k.random may be None ,这里我翻车了,
if k.random in d:
v.random = d[k.random]
return t[hot] [meta] 1609. Even Odd Tree
题目
A binary tree is named Even-Odd if it meets the following conditions:
- The root of the binary tree is at level index 0, its children are at level index 1, their children are at level index 2, etc.
- For every even-indexed level, all nodes at the level have odd integer values in strictly increasing order (from left to right).
- For every odd-indexed level, all nodes at the level have even integer values in strictly decreasing order (from left to right).
Given the root of a binary tree, return true if the binary tree is Even-Odd, otherwise return false.
Example 1:
Input: root = [1,10,4,3,null,7,9,12,8,6,null,null,2]
Output: true
Explanation: The node values on each level are:
Level 0: [1]
Level 1: [10,4]
Level 2: [3,7,9]
Level 3: [12,8,6,2]
Since levels 0 and 2 are all odd and increasing and levels 1 and 3 are all even and decreasing, the tree is Even-Odd.题解
Solve the problem by level traversing.
python
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
import queue
class Solution:
def isEvenOddTree(self, root: Optional[TreeNode]) -> bool:
if not root:
return False
level = 0
q = queue.Queue()
q.put(root)
while not q.empty():
length = q.qsize()
last_value = -1
for i in range(length):
node = q.get()
if level % 2 == 0:
if node.val % 2 == 0:
return False
if i > 0 and node.val <= last_value:
return False
if level % 2 == 1:
if node.val % 2 == 1:
return False
if i > 0 and node.val >= last_value:
return False
last_value = node.val
if node.left:
q.put(node.left)
if node.right:
q.put(node.right)
level += 1
return True复杂度
Time Complexity: O ( n ) O(n) O(n)
Space Complexity: O ( n ) O(n) O(n)
1650. Lowest Common Ancestor of a Binary Tree III
题目
Given two nodes of a binary tree p and q, return their lowest common ancestor (LCA).
Each node will have a reference to its parent node. The definition for Node is below:
class Node {
public int val;
public Node left;
public Node right;
public Node parent;
}
According to the definition of LCA on Wikipedia: "The lowest common ancestor of two nodes p and q in a tree T is the lowest node that has both p and q as descendants (where we allow a node to be a descendant of itself)."
题解1
python
"""
# Definition for a Node.
class Node:
def __init__(self, val):
self.val = val
self.left = None
self.right = None
self.parent = None
"""
class Solution:
def lowestCommonAncestor(self, p: 'Node', q: 'Node') -> 'Node':
s = set()
node = p
while node:
s.add(node)
node = node.parent
node = q
while node not in s:
node = node.parent
return node复杂度
Time Complexity: O ( n ) O(n) O(n)
Space Complexity: O ( n ) O(n) O(n)
题解2
python
"""
# Definition for a Node.
class Node:
def __init__(self, val):
self.val = val
self.left = None
self.right = None
self.parent = None
"""
class Solution:
def lowestCommonAncestor(self, p: 'Node', q: 'Node') -> 'Node':
node1 = p
node2 = q
while node1 != node2:
node1 = node1.parent if node1 else q
node2 = node2.parent if node2 else p
return node1复杂度
Time Complexity: O ( n ) O(n) O(n)
Space Complexity: O ( 1 ) O(1) O(1)
2265. Count Nodes Equal to Average of Subtree
题目
Given the root of a binary tree, return the number of nodes where the value of the node is equal to the average of the values in its subtree.
Note:
The average of n elements is the sum of the n elements divided by n and rounded down to the nearest integer.
A subtree of root is a tree consisting of root and all of its descendants.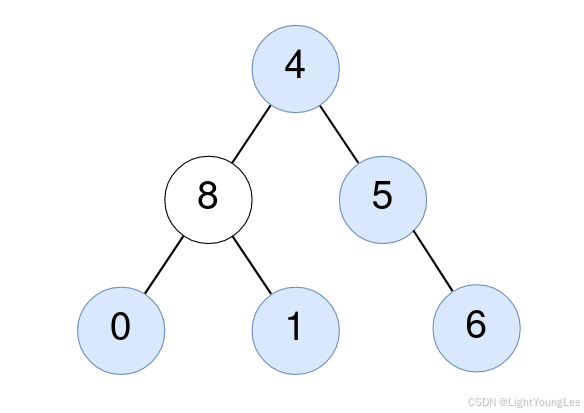
Input: root = [4,8,5,0,1,null,6]
Output: 5
Explanation:
For the node with value 4: The average of its subtree is (4 + 8 + 5 + 0 + 1 + 6) / 6 = 24 / 6 = 4.
For the node with value 5: The average of its subtree is (5 + 6) / 2 = 11 / 2 = 5.
For the node with value 0: The average of its subtree is 0 / 1 = 0.
For the node with value 1: The average of its subtree is 1 / 1 = 1.
For the node with value 6: The average of its subtree is 6 / 1 = 6.
题解
后序遍历解决问题。
python
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def __init__(self):
self.res = 0
def averageOfSubtree(self, root: TreeNode) -> int:
self.core(root)
return self.res
def core(self, root):
if not root:
return (0, 0)
left = self.core(root.left)
right = self.core(root.right)
if (left[0] + right[0] + root.val) // (left[1] + right[1] + 1) == root.val:
self.res += 1
return (left[0] + right[0] + root.val, left[1] + right[1] + 1)复杂度
Time Complexity: O ( n ) O(n) O(n)
Space Complexity: O ( n ) O(n) O(n)
LCR 143.子结构判断 E
题目
输入两棵二叉树A和B,判断B是不是A的子结构。(约定空树不是任意一个树的子结构)
B是A的子结构, 即 A中有出现和B相同的结构和节点值。
例如:
给定的树 A:
3
/ \
4 5
/ \
1 2
给定的树 B:
4
/
1
返回 true,因为 B 与 A 的一个子树拥有相同的结构和节点值。
示例 1:
输入:A = [1,2,3], B = [3,1]
输出:false
示例 2:
输入:A = [3,4,5,1,2], B = [4,1]
输出:true
限制:
0 <= 节点个数 <= 10000题解
At first we need to find whether B is the sub structure of A and B's root is anchored to A's root. If it is yes, just return True. If it is no, we need to do the same thing to A's left and right recursively.
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
bool is_sub(TreeNode* A, TreeNode* B) {
if (!B) {
return true;
}
if (!A) {
return false;
}
if (A->val != B->val) {
return false;
}
return is_sub(A->left, B->left) && is_sub(A->right, B->right);
}
bool isSubStructure(TreeNode* A, TreeNode* B) {
if (A && B) {
if (is_sub(A, B)) {
return true;
}
return isSubStructure(A->left, B) || isSubStructure(A->right, B);
}
return false;
}
};
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def is_sub(self, A, B):
if not B:
return True
if not A:
return False
if A.val != B.val:
return False
return self.is_sub(A.left, B.left) and self.is_sub(A.right, B.right)
def isSubStructure(self, A: Optional[TreeNode], B: Optional[TreeNode]) -> bool:
if A and B:
return self.is_sub(A, B) or self.isSubStructure(A.left, B) or self.isSubStructure(A.right, B)
return False复杂度
时间复杂度: O ( M N ) O(MN) O(MN),M和N代表A和B节点个数,遍历A的某个节点时,总共时间复杂度为B的节点数
空间复杂度: O ( M ) O(M) O(M),A的节点个数
Time Complexity: O(MN), where M and N represent the number of nodes in A and B respectively. When traversing a node in A, the total time complexity is equivalent to the number of nodes in B.
Space Complexity: O(M), which is determined by the number of nodes in A.
LCR 152. 验证二叉搜索树的后序遍历序列 E
题目
请实现一个函数来判断整数数组 postorder 是否为二叉搜索树的后序遍历结果。
题解
BST后序遍历序列的特点是先左子树序列,再右子树序列,最后是根节点。左子树序列的所有节点都小于根节点,右子树序列的所有节点都大于根节点。根据这个特性我们可以通过中序遍历来解决问题。
A key characteristic of the post-order traversal sequence of a Binary Search Tree (BST) is that it follows the order: left subtree sequence first, then right subtree sequence, and finally the root node. All nodes in the left subtree sequence are smaller than the root node, while all nodes in the right subtree sequence are larger than the root node. Based on this property, we can solve the problem using an in-order traversal.
cpp
class Solution {
public:
bool verifyTreeOrder(vector<int>& postorder) {
return dfs(postorder, 0, postorder.size() - 1);
}
bool dfs(vector<int>& postorder, int i, int j) {
if (i >= j) {
return true;
}
int p = i;
while (postorder[p] < postorder[j]) {
++p;
}
int m = p;
while (postorder[p] > postorder[j]) {
++p;
}
return p == j && dfs(postorder, i, m - 1) && dfs(postorder, m, j - 1);
}
};
// Python Version
class Solution:
def verifyTreeOrder(self, postorder: List[int]) -> bool:
if len(postorder) <= 2:
return True
return self.core(postorder, 0, len(postorder) - 1)
def core(self, postorder, left, right):
if left >= right:
return True
root_val = postorder[right]
idx = left
for i in range(left, right + 1):
if postorder[i] >= root_val:
idx = i
break
for i in range(idx, right + 1):
if postorder[i] <= root_val:
break
return i == right and self.core(postorder, left, idx - 1) and self.core(postorder, idx, right - 1)题解2
示例代码和注解如下所示,题解见 这里。
cpp
class Solution {
public:
bool verifyTreeOrder(vector<int>& postorder) {
stack<int> stk;
int parent = INT_MAX;
for (int i = postorder.size() - 1; i >= 0; --i) {
int cur = postorder[i];
while (!stk.empty() && stk.top() > cur) {
parent = stk.top();
stk.pop();
}
// 左子节点大于根节点,则不符合要求
if (cur > parent) {
return false;
}
stk.push(cur);
}
return true;
}
};LCR 155. 将二叉搜索树转化为排序的双向链表 E
题目
变换前:

变换后:

题解
Maintain pre and head during in-order traversal of the BST. We need to connect the head and tail node of the linked list after traversal.
cpp
/*
// Definition for a Node.
class Node {
public:
int val;
Node* left;
Node* right;
Node() {}
Node(int _val) {
val = _val;
left = NULL;
right = NULL;
}
Node(int _val, Node* _left, Node* _right) {
val = _val;
left = _left;
right = _right;
}
};
*/
// 递归版本
class Solution {
public:
Node* treeToDoublyList(Node* root) {
if (!root) {
return nullptr;
}
core(root);
head->left = pre;
pre->right = head;
return head;
}
void core(Node* cur) {
if (!cur) {
return;
}
core(cur->left);
if (pre) {
pre->right = cur;
} else {
head = cur;
}
cur->left = pre;
pre = cur;
core(cur->right);
}
private:
Node* pre;
Node* head;
};
// 迭代版本
class Solution {
public:
Node* treeToDoublyList(Node* root) {
if (!root) {
return nullptr;
}
stack<Node*> stk;
Node* pre = nullptr;
Node* head = nullptr;
while (root || !stk.empty()) {
while (root) {
stk.push(root);
root = root->left;
}
if (!stk.empty()) {
auto cur = stk.top();
stk.pop();
if (pre) {
pre->right = cur;
} else {
head = cur;
}
cur->left = pre;
pre = cur;
root = cur->right;
}
}
head->left = pre;
pre->right = head;
return head;
}
};
# Definition for a Node.
class Node:
def __init__(self, val, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def treeToDoublyList(self, root: 'Node') -> 'Node':
head = None
pre = None
if not root:
return head
stk = []
while root or len(stk) > 0:
while root:
stk.append(root)
root = root.left
node = stk.pop()
if pre:
pre.right = node
else:
head = node
node.left = pre
pre = node
root = node.right
head.left = pre
pre.right = head
return head复杂度
时间: O ( n ) O(n) O(n)
空间: O ( n ) O(n) O(n)
Time Complexity: O ( n ) O(n) O(n)
Space Complexity: O ( n ) O(n) O(n)
LCR 176. 判断是否为平衡二叉树
题目
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

输入:root = [3,9,20,null,null,15,7]
输出:true
题解1 自顶向下
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int depth(TreeNode* root) {
if (!root) {
return 0;
}
int left_depth = depth(root->left);
int right_depth = depth(root->right);
return 1 + max(left_depth, right_depth);
}
bool isBalanced(TreeNode* root) {
if (!root) {
return true;
}
int left_depth = depth(root->left);
int right_depth = depth(root->right);
if (abs(left_depth - right_depth) >= 2) {
return false;
}
return isBalanced(root->left) && isBalanced(root->right);
}
};复杂度1
时间复杂度: O ( n 2 ) O(n^2) O(n2),最坏情况为树是一条链表,整体时间复杂度为 O ( n 2 ) O(n^2) O(n2)
空间复杂度: O ( n ) O(n) O(n),递归空间
题解2 自底向上
cpp
class Solution {
public:
int depth(TreeNode* root) {
if (!root) {
return 1;
}
int left_depth = depth(root->left);
int right_depth = depth(root->right);
if (left_depth == -1 || right_depth == -1 || abs(left_depth - right_depth) >= 2) {
return -1;
}
return 1 + max(left_depth, right_depth);
}
bool isBalanced(TreeNode* root) {
return depth(root) >= 0;
}
};
// Python Version
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def depth(self, root):
if not root:
return 1
left_d = self.depth(root.left)
right_d = self.depth(root.right)
if left_d == -1 or right_d == -1 or abs(left_d - right_d) >= 2:
return -1
return 1 + max(left_d, right_d)
def isBalanced(self, root: Optional[TreeNode]) -> bool:
return self.depth(root) >= 0复杂度2
时间复杂度: O ( n ) O(n) O(n),不会重复遍历
空间复杂度: O ( n ) O(n) O(n)
剑指offer
8. 二叉树的下一个节点
题目
给定一棵二叉树和其中的一个结点,如何找出中序遍历顺序的下一个结点?树中的结点除了有两个分别指向左右子结点的指针以外,还有一个指向父结点的指针。
题解
最复杂的情况在于如果一个节点node, 它是其父节点的右节点而且没有右子树,那么就向父节点回溯,直到找到一个节点node, 如果它是它的父节点的左子节点,那么node的父节点就是我们要找到的node的下一个节点。
The most complex scenario is that if a node is the right child of its parent node and has no right subtree, we need to backtrack to the parent node until we find a node that is the left child of its parent node. In this case, the parent node of this node is the next node we are looking for.
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode *parent;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* nextNode(TreeNode* root) {
if (!root) {
return nullptr;
}
TreeNode* next_node = root->right;
if (next_node) {
while (next_node->left) {
next_node = next_node->left;
}
} else {
auto parent_node = root->parent;
while (parent_node && root == parent_node->right) { // 边界值
root = parent_node;
parent_node = parent_node->parent;
}
next_node = parent_node;
}
return next_node;
}
};复杂度
时间复杂度: O ( n ) O(n) O(n),遍历树的时间复杂度
空间复杂度: O ( 1 ) O(1) O(1),没有额外的辅助空间
Time complexity: O(n), which is the time complexity of traversing the tree.Space complexity: O(1), with no additional auxiliary space.