对于单链表相关经典算法题：206. 反转链表及876. 链表的中间结点的解析

开篇介绍：

Hello 大家，在上一篇博客中，我们一同攻克了「移除链表元素」这道单链表经典题目，对链表的基本操作有了更深入的理解。而在今天的内容里，我们将继续探索单链表领域的另外两道经典题目 ------「206. 反转链表」与「876. 链表的中间结点」。这两道题不仅是面试中的高频考点，更是深入掌握链表特性与操作技巧的绝佳练习，接下来就让我们一同深入研究吧！

在给出具体解析之前，我们依然是给出题目链接，望大家在看解析之前能够自行练手提高熟程度：

206. 反转链表 - 力扣（LeetCode）https://leetcode.cn/problems/reverse-linked-list/description/876. 链表的中间结点 - 力扣（LeetCode）https://leetcode.cn/problems/middle-of-the-linked-list/description/

206. 反转链表：

这一题也是经典中的经典了，我们先看题目：

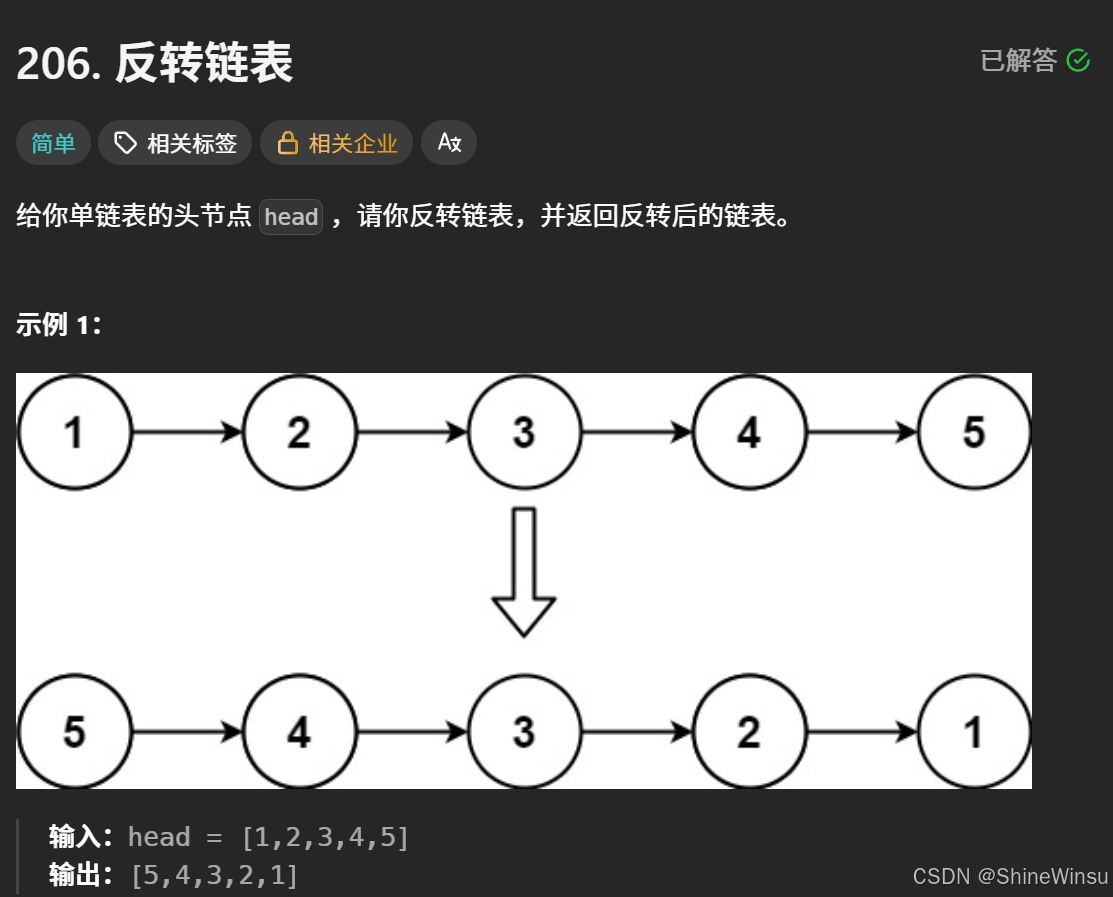
题意分析：

我们来详细地分析这道 "反转链表" 题的题意：

核心任务

给定一个单链表 的头节点 head，要对这个链表进行反转操作，最后返回反转后新链表的头节点。

单链表的结构特点回顾

单链表的每个节点包含两部分：

• 存储数据的值（比如示例里的 1、2 等）。
• 一个指针（或引用）next，指向下一个节点。通过这样的 "链式" 结构，把所有节点串联起来，形成从 "头节点" 开始，依次向后延伸的链表。

反转的具体含义

原本的链表，节点是 "从前到后" 连接的（比如示例中，1 的 next 指向 2，2 的 next 指向 3......4 的 next 指向 5）。

反转后，要让节点 "从后到前" 连接：

• 5 的 next 指向 4；
• 4 的 next 指向 3；
• ......
• 2 的 next 指向 1；
• 原本的头节点 1，反转后变成 "尾节点"，它的 next 要指向 null（表示链表到此结束）。

最终目标

完成反转后，新链表的 "头节点" 是原本链表的最后一个节点 （示例中原本的最后一个节点是 5，所以反转后新头节点是 5），且整个链表的节点连接顺序完全倒转，最后返回这个新的头节点。

简单总结：就是通过改变每个节点的 next 指向，把链表的 "方向" 完全颠倒过来，得到一个全新的、反向的单链表。

知道了题意之后，我们便可以开始着手于解题来了，在这里，我依旧是给大家提供两个方法，可以的话，大家可以把这两个方法都学习掉，帮助大家对链表的了解更进一步，同时在未来面对不同题型的时候，能够不手忙脚乱。

方法一：创建新链表

在上一篇解决移除链表元素这个问题的博客中，我给大家讲述了创建新链表的方法，那么在本道题目中，我们也依然可以使用创建新链表的方法，那么具体要如何实现呢？？且看我缓缓道来：

我们先看图：

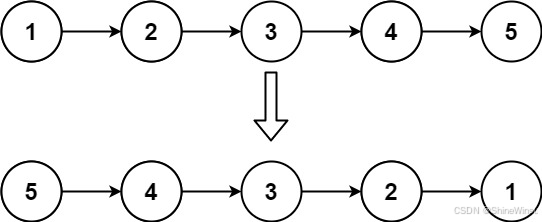
上面的链表是原链表，而下面的那一个链表，便是我们要创建的新链表，所以，我们的第一步是创建一个sl* newhead=NULL，那么问题来了，我们还需要创建sl* newtail=NULL吗？答案是：不需要，在上一篇博客中，我们是要原按链表的顺序去不断对新链表进行尾插，而且最后要传回newhead是为新链表的头结点。

而在本题中，我们同样也需要传回newhead是为新链表的头结点，但是在本题中，我们是用尾插去对新链表插入新节点的吗？很明显，并不是，就按照上图来说，我们首先要把原链表的节点1插入新链表，接着再把原链表的节点2插到新链表中，那么它要插在节点1前面还是后面呢？看了上图中的下面的链表，我们便能知道了，我们要把节点2插入到节点1的前面去，那么这就很明显了，是头插法。

那么在这里大家可能会有些疑问，为什么我们不能先把原链表的节点5插入新链表中，然后再使用尾插去把原链表的节点4插入到新链表的节点5之后呢？其实这是因为，我们的原链表是单向链表，我们只能从节点1去往后找，却不能从节5去往前找，所以，这个设想也就无法实现了，我们还是只能使用头插法。

因此，newtail也就没有它的事了，在本题中，它可以好好休息一番，那么我们要怎么实现头插呢？

大家再看图，在原链表中，是节点5的next指针指向NULL，而在新链表中，是节点1中的next指针指向NULL，而在使用头插时，很明显我们是先把原链表的节点1插入到新链表中，换句话来说就是，我们要把插入新链表的原链表的节点1的next指针设置为NULL，而这，要怎么与我们的newhead挂钩呢？

聪明的你其实很快就能发现，在对newhead初始化的时候，我们便是把它初始化为NULL，而这，不正好和我们要把插入新链表的原链表的节点1的next指针设置为NULL这一目的相同吗，所以，我们就可以这么写：

sl* newhead=NULL;
sl* temp=head;
while(temp!=NULL)
{
     //此处也有代码
     temp->next=newhead;
     //此处还有代码
     temp=temp->next;
}

大家要注意，这可不是巧合，而是必然的结果，等看到后面，大家就会知道了。

针对这段代码，我们模拟一下，首先，原链表的节点1传入，节点1的next指针变为newhead（即NULL），接下来，temp要移动到原链表的节点1的下一个节点，执行temp=temp->next，那么，能正常运行吗？大家不妨想一想，在temp->next=newhead;中，我们已经把temp->next赋值为NULL了，那temp=temp->next不就是相当于把temp赋值为NULL吗，那怎么可能找得到原链表的节点1的下一个节点呢？

所以，针对这个情况，我们就得在temp->next=newhead;之前设置变量去保存temp->next，避免在经过temp->next=newhead找不到下一个节点，具体代码如下：

while (temp != NULL)
{
    // 保存当前节点的下一个节点地址
    // 因为接下来要修改当前节点的next指针，若不提前保存会丢失后续节点
    sl* temp1 = temp->next;
    
    // 将当前节点的next指针指向新的头节点（即原链表中当前节点的前一个节点）
    // 这一步是实现反转的核心操作，改变指针方向
    temp->next = newhead;
    
    // ...（后续还需更新newhead和temp指针，继续处理下一个节点）
}

做完上述这些之后，我们离完成也就不远了，我们接下来还得对newhead进行更新才行，那么要让newhea更新为什么呢？

大家不妨想一想，我们在把原链表的节点1传进新链表之后，我们随后在下一个循环肯定还要把原链表的节点2传进新链表的节点1之前，但是为了能够实现单向链表的联系，我们得想办法让这个节点2的next指针指向新链表的节点1（同时也是原链表的节点1），而我们又知道，能够改变节点的next指针的操作是temp->next = newhead;这一行代码，换句话说就是，如果我们想要实现让这个节点2的next指针指向新链表的节点1（同时也是原链表的节点1），我们就得让temp->next = newhead中的newhead随之变成节点1的地址，而节点1的地址又出现在哪呢？很明显，就是temp，于是，我们知道如何更新newhead了。即如此newhead=temp；

完整代码如下：

typedef struct ListNode sl;

struct ListNode* reverseList(struct ListNode* head) 
{
    if (head == NULL)
    {
        return NULL;
    }
    
    sl* newhead = NULL;
    sl* temp = head;
    
    while (temp != NULL)
    {
        sl* temp1 = temp->next;
        temp->next = newhead;
        newhead = temp;
        temp = temp1;
    }
    
    return newhead;
}

为了加深大家理解，我们再给出详细例子：

我们继续用 1 -> 2 -> 3 -> 4 -> 5 -> NULL 这个例子，结合代码逐行拆解每一步的内存状态和指针变化，让每个细节都清晰可见。

初始状态（进入函数前）

• 原链表结构（内存中）： plaintext

  节点1：值=1，next=节点2的地址
  节点2：值=2，next=节点3的地址
  节点3：值=3，next=节点4的地址
  节点4：值=4，next=节点5的地址
  节点5：值=5，next=NULL（空地址）

• 函数参数：head 指向 节点 1 的地址

步骤 1：判断空链表

if (head == NULL) { return NULL; }

• 当前 head 指向节点 1（非空），所以跳过此分支，继续执行。

步骤 2：初始化指针

sl* newhead = NULL;  // 反转后链表的头（初始指向空地址）
sl* temp = head;     // 遍历指针，初始指向head（即节点1的地址）

• 此时指针状态：
  • newhead → NULL（空地址）
  • temp → 节点 1 的地址

进入循环：while (temp != NULL)

循环条件：只要 temp 指向的不是空地址（还有节点要处理），就继续循环。

第一次循环（处理节点 1）

1. 保存下一个节点地址

   sl* temp1 = temp->next;  // temp->next是节点1的next，即节点2的地址

   • temp1 现在指向 节点 2 的地址。

2. 反转当前节点的指向

   temp->next = newhead;  // temp是节点1的地址，让节点1的next指向newhead（即NULL）

   • 节点 1 的 next 从 "节点 2 的地址" 改为 "NULL"。
     此时节点 1 的状态：值=1，next=NULL。

3. 更新新链表的头

   newhead = temp;  // newhead从NULL改为temp（即节点1的地址）

   • 现在 newhead 指向节点 1（反转后链表的临时头）。

4. 移动遍历指针

   temp = temp1;  // temp从节点1的地址改为temp1（即节点2的地址）

   • 此时 temp 指向节点 2，准备处理下一个节点。

• 第一次循环后状态 ：
  • 反转链表片段：1 -> NULL（newhead 指向节点 1）
  • 剩余未处理节点：2 -> 3 -> 4 -> 5 -> NULL（temp 指向节点 2）

第二次循环（处理节点 2）

1. 保存下一个节点地址

   sl* temp1 = temp->next;  // temp是节点2的地址，其next是节点3的地址

   • temp1 指向 节点 3 的地址。

2. 反转当前节点的指向

   temp->next = newhead;  // 节点2的next从"节点3的地址"改为"newhead（节点1的地址）"

   • 节点 2 的状态：值=2，next=节点1的地址。

3. 更新新链表的头

   newhead = temp;  // newhead从节点1的地址改为节点2的地址

   • 现在 newhead 指向节点 2（反转后链表的临时头）。

4. 移动遍历指针

   temp = temp1;  // temp从节点2的地址改为节点3的地址

• 第二次循环后状态 ：
  • 反转链表片段：2 -> 1 -> NULL（newhead 指向节点 2）
  • 剩余未处理节点：3 -> 4 -> 5 -> NULL（temp 指向节点 3）

第三次循环（处理节点 3）

1. temp1 = temp->next → temp1 指向 节点 4 的地址（节点 3 的 next）。
2. temp->next = newhead → 节点 3 的 next 从 "节点 4 的地址" 改为 "节点 2 的地址"（newhead 当前指向节点 2）。
   • 节点 3 状态：值=3，next=节点2的地址。
3. newhead = temp → newhead 指向节点 3。
4. temp = temp1 → temp 指向节点 4。

• 第三次循环后状态 ：
  • 反转链表片段：3 -> 2 -> 1 -> NULL
  • 剩余节点：4 -> 5 -> NULL（temp 指向节点 4）

第四次循环（处理节点 4）

1. temp1 = temp->next → temp1 指向 节点 5 的地址（节点 4 的 next）。
2. temp->next = newhead → 节点 4 的 next 从 "节点 5 的地址" 改为 "节点 3 的地址"（newhead 指向节点 3）。
   • 节点 4 状态：值=4，next=节点3的地址。
3. newhead = temp → newhead 指向节点 4。
4. temp = temp1 → temp 指向节点 5。

• 第四次循环后状态 ：
  • 反转链表片段：4 -> 3 -> 2 -> 1 -> NULL
  • 剩余节点：5 -> NULL（temp 指向节点 5）

第五次循环（处理节点 5）

1. temp1 = temp->next → temp1 指向 NULL（节点 5 的 next 是 NULL）。
2. temp->next = newhead → 节点 5 的 next 从 "NULL" 改为 "节点 4 的地址"（newhead 指向节点 4）。
   • 节点 5 状态：值=5，next=节点4的地址。
3. newhead = temp → newhead 指向节点 5。
4. temp = temp1 → temp 指向 NULL（因为temp1是 NULL）。

• 第五次循环后状态 ：
  • 反转链表完整：5 -> 4 -> 3 -> 2 -> 1 -> NULL（newhead 指向节点 5）
  • temp 指向 NULL，循环结束。

循环结束，返回结果

return newhead;  // newhead指向节点5的地址

最终得到的反转链表为：5 -> 4 -> 3 -> 2 -> 1 -> NULL，与预期完全一致。

核心逻辑总结

每次循环都在做 3 件事：

1. 用temp1"记住" 下一个节点，防止丢失。
2. 让当前节点的next"回头" 指向已反转的部分（newhead）。
3. 移动newhead到当前节点（它成为新的反转头部），并让temp继续遍历下一个节点。

整个过程像 "拆链条再反向重组"，每个节点都被依次接到新链表的最前面，最终实现全链表反转。

方法二：三指针迭代法

这一个方法，就是不需要创建新链表，而是借助三个指针去不断移动，具体原理如下：

这个三指针迭代法反转链表的原理可以这样理解：

1. 核心思路：通过三个指针逐步遍历链表，逐个改变节点的指向关系，从而实现整个链表的反转。

2. 指针分工：

   • n1：始终指向已经完成反转的部分的头节点（初始为NULL，因为开始时没有任何节点被反转）
   • n2：指向当前正在处理的节点（初始为原链表的头节点head）
   • n3：临时保存n2的下一个节点（用于继续遍历未处理的部分）

3. 迭代过程：

   • 每次循环中，先用n3记录n2的下一个节点（防止链表断裂）
   • 然后将n2的指针反转，指向n1（完成当前节点的反转）
   • 接着将n1移动到n2的位置（n1始终是已反转部分的新头部）
   • 最后将n2移动到n3的位置（准备处理下一个节点）

4. 终止条件：

   • 当n2变为NULL时，说明所有节点都已处理完毕
   • 此时n1正好指向原链表的最后一个节点，也就是反转后新链表的头节点

5. 特殊情况处理：

   • 如果原链表为空（head == NULL），直接返回NULL

通过这种方式，只需一次遍历（时间复杂度 O (n)）和常数级的额外空间（空间复杂度 O (1)），就能高效地完成链表反转。

下面详细代码：

//三指针迭代法：
typedef struct ListNode sl;

struct ListNode* reverseList(struct ListNode* head) 
{
    if(head==NULL)//为空链表或者只有一个节点
    {
        return NULL;
    }
    sl* n1=NULL;
    sl* n2=head;
    while(n2!=NULL)
    {
        sl* n3=n2->next;
        n2->next=n1;
        n1=n2;
        n2=n3;
    }
    return n1;
}

这个方法可以说是非常的简便，在每一次循环中，我们只让n2节点的next指针指向n1

，并没有让n3的next指针指向n2 ，在进行完让n2节点的next指针指向n1之后，我们便让n1、n2都往退一个节点，设置n3的作用便是保存n2的next指针，使得n2能够顺利的移动到下一个节点，而n1移动到下一个节点（也就是n2），也是非常简单，因为我们虽然修改了n2的next指针让其指向n节点，但在n2没移动到n2的下一个节点之前，n2还是n1的后一个节点，所以我们就可以直接将n2赋值给n1，这样子也就实现了n1的后移一个节点，之后我们再让n2移动到n2的下一个节点去，也就是将n32赋值给n2.

所以大家也就知道了

sl* n3=n2->next;
n2->next=n1;
n1=n2;
n2=n3;

这一串的顺序是固定的，是不能变的。

下面我给大家一个方法二代码的详细例子，帮助大家理解：

我们来用细致的步骤，结合每一步的内存结构变化，彻底解析三指针反转链表的过程。以链表 1 -> 2 -> 3 -> 4 -> NULL 为例，我们会跟踪每个指针的内存地址指向和链表节点的连接关系。

准备知识

• 链表节点结构：每个节点包含「值」和「next 指针」（指向后一个节点）

• 指针本质：存储节点的内存地址（例如 n2 = 1 表示 n2 存储节点 1 的内存地址）

• 原链表内存分布（简化表示）：

  节点1：值=1，next→节点2的地址
  节点2：值=2，next→节点3的地址
  节点3：值=3，next→节点4的地址
  节点4：值=4，next→NULL（空地址）

初始状态（循环开始前）

• 指针初始化：

  • n1 = NULL（不指向任何节点，存储空地址）
  • n2 = head（head 是节点 1 的地址，所以 n2 指向节点 1）
  • n3 未赋值（还未指向任何节点）

• 链表连接：节点1.next → 节点2，节点2.next → 节点3，节点3.next → 节点4，节点4.next → NULL

• 可视化：

  n1: [NULL]
  n2: [节点1的地址] → 节点1: (值=1, next→节点2)
  n3: [未赋值]
  剩余链表：节点2 → 节点3 → 节点4 → NULL

第一次循环（处理节点 1）

步骤 1：用 n3 保存 n2 的下一个节点

• 执行 n3 = n2->next

  • n2 指向节点 1，n2->next 是节点 1 的 next 指针（即节点 2 的地址）
  • 所以 n3 现在存储节点 2 的地址（指向节点 2）

• 状态：

  n1: [NULL]
  n2: [节点1的地址] → 节点1: (值=1, next→节点2)
  n3: [节点2的地址] → 节点2: (值=2, next→节点3)

  这一步的核心：提前记住节点 1 的下一个节点，防止后续修改节点 1 的指向后丢失链表

步骤 2：反转 n2 的指向（关键操作）

• 执行 n2->next = n1

  • n2 指向节点 1，修改节点 1 的 next 指针，让它指向 n1（即 NULL）
  • 节点 1 原本指向节点 2，现在改为指向 NULL

• 状态：

  n1: [NULL]
  n2: [节点1的地址] → 节点1: (值=1, next→NULL)  ← 指向已改变
  n3: [节点2的地址] → 节点2: (值=2, next→节点3)

  此时节点 1 已从原链表脱离，成为一个独立的反转节点（指向 NULL）

步骤 3：移动 n1 到当前节点（n2 的位置）

• 执行 n1 = n2

  • n2 存储节点 1 的地址，所以 n1 现在也存储节点 1 的地址（指向节点 1）

• 状态：

  n1: [节点1的地址] → 节点1: (值=1, next→NULL)  ← n1移动到这里
  n2: [节点1的地址] → 节点1: (值=1, next→NULL)
  n3: [节点2的地址] → 节点2: (值=2, next→节点3)

  n1 的作用：标记「已完成反转的链表部分」的头节点，现在已反转部分是「节点 1→NULL」

步骤 4：移动 n2 到下一个节点（n3 的位置）

• 执行 n2 = n3

  • n3 存储节点 2 的地址，所以 n2 现在存储节点 2 的地址（指向节点 2）

• 状态：

  n1: [节点1的地址] → 节点1: (值=1, next→NULL)
  n2: [节点2的地址] → 节点2: (值=2, next→节点3)  ← n2移动到这里
  n3: [节点2的地址] → 节点2: (值=2, next→节点3)

  n2 的作用：标记「当前需要处理的节点」，现在准备处理节点 2

• 第一次循环结束后：

  • 已反转部分：节点1 → NULL
  • 未处理部分：节点2 → 节点3 → 节点4 → NULL

第二次循环（处理节点 2）

步骤 1：用 n3 保存 n2 的下一个节点

• 执行 n3 = n2->next

  • n2 指向节点 2，n2->next 是节点 3 的地址
  • n3 现在指向节点 3

• 状态：

  n1: [节点1的地址] → 节点1: (值=1, next→NULL)
  n2: [节点2的地址] → 节点2: (值=2, next→节点3)
  n3: [节点3的地址] → 节点3: (值=3, next→节点4)

步骤 2：反转 n2 的指向

• 执行 n2->next = n1

  • 修改节点 2 的 next 指针，从指向节点 3 改为指向 n1（即节点 1 的地址）

• 状态：

  n1: [节点1的地址] → 节点1: (值=1, next→NULL)
  n2: [节点2的地址] → 节点2: (值=2, next→节点1)  ← 指向已改变
  n3: [节点3的地址] → 节点3: (值=3, next→节点4)

  此时节点 2 与节点 1 连接，形成「节点 2→节点 1→NULL」的反转片段

步骤 3：移动 n1 到当前节点

• 执行 n1 = n2

  • n1 从指向节点 1 改为指向节点 2（现在已反转部分的头是节点 2）

• 状态：

  n1: [节点2的地址] → 节点2: (值=2, next→节点1)  ← n1移动到这里
  n2: [节点2的地址] → 节点2: (值=2, next→节点1)
  n3: [节点3的地址] → 节点3: (值=3, next→节点4)

步骤 4：移动 n2 到下一个节点

• 执行 n2 = n3

  • n2 从指向节点 2 改为指向节点 3（准备处理节点 3）

• 状态：

  n1: [节点2的地址] → 节点2: (值=2, next→节点1)
  n2: [节点3的地址] → 节点3: (值=3, next→节点4)  ← n2移动到这里
  n3: [节点3的地址] → 节点3: (值=3, next→节点4)

• 第二次循环结束后：

  • 已反转部分：节点2 → 节点1 → NULL
  • 未处理部分：节点3 → 节点4 → NULL

第三次循环（处理节点 3）

步骤 1：用 n3 保存 n2 的下一个节点

• 执行 n3 = n2->next

  • n2 指向节点 3，n2->next 是节点 4 的地址
  • n3 现在指向节点 4

• 状态：

  n1: [节点2的地址] → 节点2: (值=2, next→节点1)
  n2: [节点3的地址] → 节点3: (值=3, next→节点4)
  n3: [节点4的地址] → 节点4: (值=4, next→NULL)

步骤 2：反转 n2 的指向

• 执行 n2->next = n1

  • 节点 3 的 next 指针从指向节点 4 改为指向 n1（即节点 2 的地址）

• 状态：

  n1: [节点2的地址] → 节点2: (值=2, next→节点1)
  n2: [节点3的地址] → 节点3: (值=3, next→节点2)  ← 指向已改变
  n3: [节点4的地址] → 节点4: (值=4, next→NULL)

  反转片段变为「节点 3→节点 2→节点 1→NULL」

步骤 3：移动 n1 到当前节点

• 执行 n1 = n2

  • n1 从指向节点 2 改为指向节点 3（已反转部分的头更新为节点 3）

• 状态：

  n1: [节点3的地址] → 节点3: (值=3, next→节点2)  ← n1移动到这里
  n2: [节点3的地址] → 节点3: (值=3, next→节点2)
  n3: [节点4的地址] → 节点4: (值=4, next→NULL)

步骤 4：移动 n2 到下一个节点

• 执行 n2 = n3

  • n2 从指向节点 3 改为指向节点 4（准备处理节点 4）

• 状态：

  n1: [节点3的地址] → 节点3: (值=3, next→节点2)
  n2: [节点4的地址] → 节点4: (值=4, next→NULL)  ← n2移动到这里
  n3: [节点4的地址] → 节点4: (值=4, next→NULL)

• 第三次循环结束后：

  • 已反转部分：节点3 → 节点2 → 节点1 → NULL
  • 未处理部分：节点4 → NULL

第四次循环（处理节点 4）

步骤 1：用 n3 保存 n2 的下一个节点

• 执行 n3 = n2->next

  • n2 指向节点 4，n2->next 是 NULL（空地址）
  • n3 现在存储 NULL

• 状态：

  n1: [节点3的地址] → 节点3: (值=3, next→节点2)
  n2: [节点4的地址] → 节点4: (值=4, next→NULL)
  n3: [NULL]

步骤 2：反转 n2 的指向

• 执行 n2->next = n1

  • 节点 4 的 next 指针从指向 NULL 改为指向 n1（即节点 3 的地址）

• 状态：

  n1: [节点3的地址] → 节点3: (值=3, next→节点2)
  n2: [节点4的地址] → 节点4: (值=4, next→节点3)  ← 指向已改变
  n3: [NULL]

  反转片段变为「节点 4→节点 3→节点 2→节点 1→NULL」

步骤 3：移动 n1 到当前节点

• 执行 n1 = n2

  • n1 从指向节点 3 改为指向节点 4（已反转部分的头更新为节点 4）

• 状态：

  n1: [节点4的地址] → 节点4: (值=4, next→节点3)  ← n1移动到这里
  n2: [节点4的地址] → 节点4: (值=4, next→节点3)
  n3: [NULL]

步骤 4：移动 n2 到下一个节点

• 执行 n2 = n3

  • n2 从指向节点 4 改为指向 NULL（所有节点已处理完毕）

• 状态：

  n1: [节点4的地址] → 节点4: (值=4, next→节点3)
  n2: [NULL]
  n3: [NULL]

循环终止与结果

• 当 n2 = NULL 时，循环条件 n2 != NULL 不成立，循环结束
• 此时 n1 指向的节点 4，正是反转后链表的头节点
• 最终反转链表：4 → 3 → 2 → 1 → NULL

核心逻辑提炼 ：

三指针的每一步都是「保存下一个节点→反转当前节点指向→移动指针到下一个位置」的重复。n3 像 "探路者" 提前记住下一步，n2 像 "工人" 执行反转操作，n1 像 "标记杆" 记录已完成的部分。整个过程没有创建新节点，只是修改指针指向，因此空间效率极高，时间上只需遍历一次链表，是最优的链表反转方案。

由此，206. 反转链表题目大功告成，其实本题还有递归解法，但是它不太适用于大链表，容易造成栈溢出，所以我就不多介绍，感兴趣的可以自行摸索一番。

876. 链表的中间结点：

接下来的这一题，同样是不难的一道题，我们先看题目：

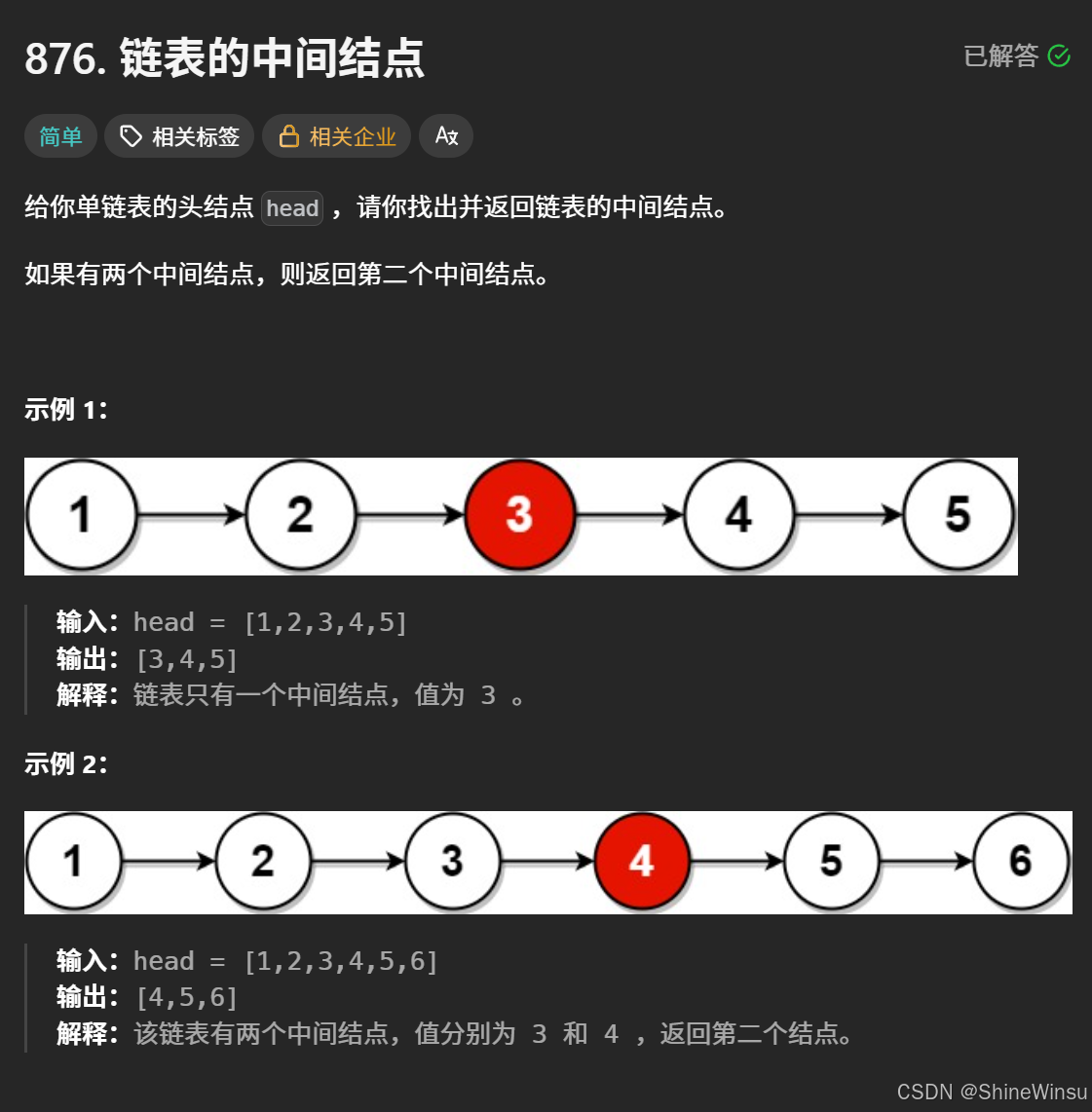
题意分析：

我们来细致地剖析这道 "寻找链表中间节点" 的题目，从需求、示例到解法逻辑层层拆解。

一、题目核心需求的精准理解

给定单链表的头节点 head，要定位并返回中间节点，规则如下：

• 节点数为奇数：比如有 n=2k+1 个节点（k 为非负整数，如 n=5 时 k=2），中间节点是第 k+1 个（如 5 个节点时，第 3 个）。
• 节点数为偶数 ：比如有 n=2k 个节点（如 n=6 时 k=3），中间节点有两个（第 k 和 k+1 个），要求返回 第二个（如 6 个节点时，第 4 个）。

二、示例的深度解析

通过具体示例，直观感受规则如何作用：

示例 1：奇数个节点（n=5）

• 链表结构：1 -> 2 -> 3 -> 4 -> 5
• 节点数 n=5，满足 n=2k+1（k=2），中间节点是第 k+1=3 个。
• 所以返回值为 3 的节点，后续节点 4 -> 5 也会被包含（因为链表是 "链式" 结构，返回中间节点后，其后续节点仍通过 next 连接）。

示例 2：偶数个节点（n=6）

• 链表结构：1 -> 2 -> 3 -> 4 -> 5 -> 6
• 节点数 n=6，满足 n=2k（k=3），中间节点是第 k=3 和 k+1=4 个。
• 按要求返回 第二个 中间节点（第 4 个），即值为 4 的节点，后续节点 5 -> 6 也会被包含。

那么，对于本题，我依然是给大家提供两种方法，大家自行参考

方法一：计数法

这第一个方法，就是非常朴素的一个做法，因为我们经过题意分析知道，题目是要求我们去把一个链表的中间的节点表达出来，那么，我们可以先去计数这个链表中有几个节点，然后再把这个数量除2，不就能得到中间节点的数量是多少了，当然，这只是我们的总思路，具体实现还需要进一步细化。

首先，我们需要设置一个变量count负责计数链表中有几个节点，这需要我们去遍历链表，不过在这之前，我们要思考一下，我们要对count初始化为多少呢？0？还是1？答案是：还是初始化为0，我们再看题目示例

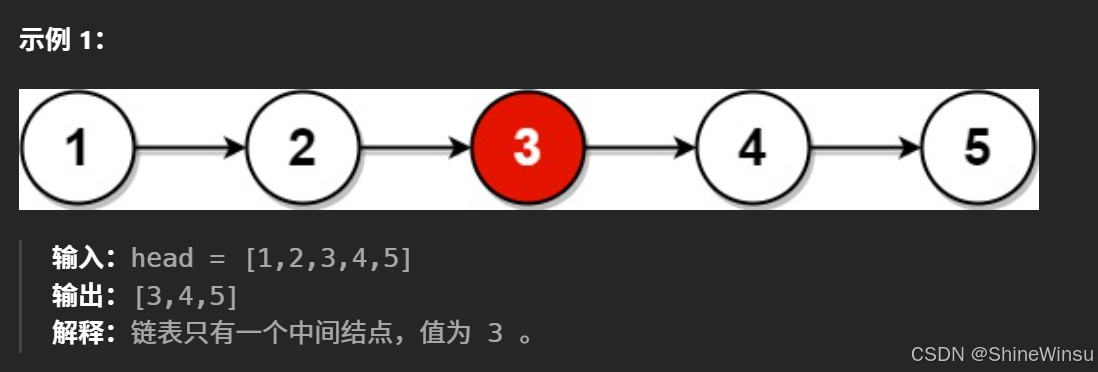
如果我们把count初始化为0的话，那会计数出链表只有5个节点，而要是初始化为1的话，就会计数出链表有6个节点，具体代码如下：

// 统计链表节点数量
sl* temp = head;  // 定义临时指针指向头节点
int count = 0;    // 计数器初始化为0

// 遍历链表计数
while (temp != NULL) {
    count++;           // 节点数加1
    temp = temp->next; // 指针后移
}

大家可以结合着代码进行理解。在这里，我再次强调一下，count++与temp = temp->next;的顺序怎么调换都行，大家不用担心

在实现了计数之后，我们就得想办法表达出链表中间节点的数据了，而这肯定又需要我们的count了，那么要怎么实现呢？

首先，我们要定义half=count/2，这样子算是记录到链表的中间节点所在的位置，接下来，我们就得借助while循环了，while（half），接着再去不断移动指针位置，移动一次便half--一次，当half减为0之后，也就代表着指针移动到了中间节点的位置，详细代码如下：

// 计算需要移动的步数（中间节点位置）
int half = count / 2;

// 第二次遍历：定位到中间节点
sl* temp1 = head;
while (half > 0) 
{
    temp1 = temp1->next;  // 指针后移
    half--;               // 剩余步数减1
}

在这里，我再次强调一下，half--与temp1 = temp1->next;的顺序怎么调换都行，大家不用担心，详情见对于牛客网---语言学习篇---编程初学者入门训练---水仙花数与变种水仙花数及类似题目的分析-CSDN博客

到此，我们便可以把代码完整串联起来了：

计数法：

typedef struct ListNode sl;

struct ListNode* middleNode(struct ListNode* head) 
{
    sl* temp=head;
    int count=0;//计数有几个节点
    while(temp!=NULL)
    {
        count++;
        temp=temp->next;
    }
    int half=count/2;
    sl* temp1=head;
    while(half)
    {
        temp1=temp1->next;
        half--;
    }
    return temp1;
}

不知道大家有没有这么一个疑问，我们的half是直接count/2，可是count为奇数时，比如5，half就是2，count为偶数时，比如6，那么half就是3，可是按道理来说，我们的5个节点的时候，我们是要表达出第3个节点的数据的，是6个节点的时候，我们是要表达出第3个节点的数据的，这怎么看都不符合half呀？，我们是不是应该给half加一呢？

其实，是不用的，因为（最主要的原因就是我们用的是while（half），所以half是指要移动几步，而指针又是从第一个节点开始移动的）：

要理解为什么不需要给 half 加一，我们需要结合链表的遍历逻辑 和整数除法的特性来分析

1. 链表的 "从 0 开始移动" 特性

链表的节点访问是从 head 开始，通过 next 指针逐步后移的。

• 当 half = count / 2 时，half 表示的是 "需要移动的步数"，而不是 "目标节点的索引"。

举个例子：

• 对于 5 个节点的链表（节点索引 1~5）：

  • count = 5，half = 5 / 2 = 2（整数除法）。
  • 从 head（第 1 个节点）开始，移动 2 步：
    • 第 1 步：到第 2 个节点；
    • 第 2 步：到第 3 个节点（中间节点）。
  • 正好符合 "5 个节点时返回第 3 个节点" 的需求。

• 对于 6 个节点的链表（节点索引 1~6）：

  • count = 6，half = 6 / 2 = 3。
  • 从 head（第 1 个节点）开始，移动 3 步：
    • 第 1 步：到第 2 个节点；
    • 第 2 步：到第 3 个节点；
    • 第 3 步：到第 4 个节点（第二个中间节点）。
  • 正好符合 "6 个节点时返回第 4 个节点" 的需求。

2. 整数除法的 "天然适配"

整数除法（count / 2）的结果，恰好能匹配 "移动步数" 的需求：

• 奇数 count：count = 2k + 1（如 k=2 时，count=5），half = k（5/2=2）。

  移动 k 步后，正好到达第 k+1 个节点（中间节点）。

• 偶数 count：count = 2k（如 k=3 时，count=6），half = k（6/2=3）。

  移动 k 步后，正好到达第 k+1 个节点（第二个中间节点）。

3. 反证：如果加一，会发生什么？

假设给 half 加一（即 half = count / 2 + 1）：

• 对于 5 个节点：half = 5/2 + 1 = 2 + 1 = 3。

  从 head 移动 3 步，会到达第 4 个节点（错误，应该返回第 3 个）。

• 对于 6 个节点：half = 6/2 + 1 = 3 + 1 = 4。

  从 head 移动 4 步，会到达第 5 个节点（错误，应该返回第 4 个）。

总结

half = count / 2 不需要加一，因为：

• half 表示的是 "从 head 开始需要移动的步数"，而非 "目标节点的索引"。
• 整数除法的结果，天然能让移动 half 步后，精准定位到题目要求的中间节点（奇数返回唯一中间，偶数返回第二个中间）。

再给大家一个例子，帮助大家理解：

我们以两个具体示例（奇数个节点和偶数个节点），用 "内存地址可视化" 的方式，逐行拆解计数法寻找中间节点的每一步细节。

前提准备

• 链表节点结构：每个节点包含 val（值）和 next（指向后一个节点的指针）
• 假设节点内存地址简化表示为：节点 1 地址 = 0x100，节点 2=0x200，节点 3=0x300，节点 4=0x400，节点 5=0x500，节点 6=0x600，NULL=0x000

示例 1：奇数个节点（1->2->3->4->5）

链表初始状态：

节点1（0x100）：val=1，next=0x200（指向节点2）
节点2（0x200）：val=2，next=0x300（指向节点3）
节点3（0x300）：val=3，next=0x400（指向节点4）
节点4（0x400）：val=4，next=0x500（指向节点5）
节点5（0x500）：val=5，next=0x000（指向NULL）
head = 0x100（指向节点1）

步骤 1：第一次遍历统计节点总数（count）

代码片段：

struct ListNode* temp = head;  // temp初始指向head（0x100）
int count = 0;                 // 计数器初始化为0

while (temp != NULL) {
    count++;
    temp = temp->next;
}

遍历过程逐行拆解：

1. 初始状态 ：temp = 0x100（指向节点 1），count = 0
2. 第 1 次进入循环 （temp=0x100≠NULL）：
   • count++ → count=1（统计到节点 1）
   • temp = temp->next → temp=0x200（节点 1 的 next 是 0x200，指向节点 2）
3. 第 2 次循环 （temp=0x200≠NULL）：
   • count++ → count=2（统计到节点 2）
   • temp = temp->next → temp=0x300（指向节点 3）
4. 第 3 次循环 （temp=0x300≠NULL）：
   • count++ → count=3（统计到节点 3）
   • temp = temp->next → temp=0x400（指向节点 4）
5. 第 4 次循环 （temp=0x400≠NULL）：
   • count++ → count=4（统计到节点 4）
   • temp = temp->next → temp=0x500（指向节点 5）
6. 第 5 次循环 （temp=0x500≠NULL）：
   • count++ → count=5（统计到节点 5）
   • temp = temp->next → temp=0x000（节点 5 的 next 是 NULL）
7. 循环结束 ：temp=0x000（NULL），退出循环，此时 count=5（总节点数为 5）

步骤 2：计算需要移动的步数（half）

代码：int half = count / 2;

• 计算：half = 5 / 2 = 2（整数除法，结果为 2）
• 含义：从 head 开始，需要向后移动 2 步才能到达中间节点

步骤 3：第二次遍历定位中间节点

代码片段：

struct ListNode* temp1 = head;  // temp1初始指向head（0x100）
while (half > 0) {
    temp1 = temp1->next;
    half--;
}

循环过程逐行拆解：

1. 初始状态 ：temp1=0x100（指向节点 1），half=2
2. 第 1 次循环 （half=2>0）：
   • temp1 = temp1->next → temp1=0x200（从节点 1 移到节点 2）
   • half-- → half=1
3. 第 2 次循环 （half=1>0）：
   • temp1 = temp1->next → temp1=0x300（从节点 2 移到节点 3）
   • half-- → half=0
4. 循环结束 ：half=0，退出循环
5. 最终结果 ：temp1=0x300（指向节点 3），即中间节点

示例 2：偶数个节点（1->2->3->4->5->6）

链表初始状态：

节点1（0x100）：val=1，next=0x200
节点2（0x200）：val=2，next=0x300
节点3（0x300）：val=3，next=0x400
节点4（0x400）：val=4，next=0x500
节点5（0x500）：val=5，next=0x600
节点6（0x600）：val=6，next=0x000
head = 0x100

步骤 1：第一次遍历统计节点总数（count）

• 遍历过程类似示例 1，最终统计得 count=6（总节点数为 6）

步骤 2：计算需要移动的步数（half）

• 计算：half = 6 / 2 = 3
• 含义：从 head 开始，需要向后移动 3 步才能到达第二个中间节点

步骤 3：第二次遍历定位中间节点

循环过程：

1. 初始状态 ：temp1=0x100（节点 1），half=3
2. 第 1 次循环 ：temp1=0x200（节点 2），half=2
3. 第 2 次循环 ：temp1=0x300（节点 3），half=1
4. 第 3 次循环 ：temp1=0x400（节点 4），half=0
5. 最终结果 ：temp1=0x400（指向节点 4），即第二个中间节点

核心逻辑总结

计数法的本质是 "先知道总长度，再计算中间位置"：

1. 第一次遍历：通过count变量记录链表总节点数（必须完整遍历一次）
2. 计算中间位置：利用整数除法count/2，天然适配 "奇数返回中间，偶数返回第二个中间" 的规则
3. 第二次遍历：从 head 移动count/2步，精准定位到目标节点

整个过程共遍历链表两次，时间复杂度 O (n)，空间复杂度 O (1)，逻辑简单且稳定，适合新手理解链表的基本操作。

方法二：快慢指针法

这个方法，就是智慧法了，叫作快慢指针法，下面解释一下它的原理：

我们从 "物理运动模拟" 和 "数学公式推导" 两个维度，更细致地拆解快慢指针法的核心原理，结合每一步的指针状态变化，彻底说清为什么快指针到终点时，慢指针一定在中间。

一、物理运动视角：用 "同步赛跑" 模拟指针运动

把链表想象成一条直线跑道，每个节点是一个标记点，终点在最后一个节点的右侧（NULL 位置）。

• 慢指针（slow）是 "慢跑者"，每秒跑 1 个节点（1 步 / 次）。
• 快指针（fast）是 "快跑者"，每秒跑 2 个节点（2 步 / 次）。
• 两人同时从起点（head）出发，当快跑者到达终点时，慢跑者的位置就是中间点。

场景 1：奇数个节点（n=5，节点 1→2→3→4→5）

• 跑道长度：5 个节点，终点在节点 5 右侧（NULL）。

• 快跑者（fast）的运动过程：

  • 初始位置：节点 1
  • 第 1 秒：跑 2 步→节点 3（1→2→3）
  • 第 2 秒：跑 2 步→节点 5（3→4→5）
  • 此时，快跑者到达 "最后一个节点"，再跑就会出界（fast->next=NULL），停止运动。
  • 总运动时间：2 秒，总路程：4 步（2 秒 ×2 步 / 秒）。

• 慢跑者（slow）的运动过程：

  • 初始位置：节点 1
  • 第 1 秒：跑 1 步→节点 2
  • 第 2 秒：跑 1 步→节点 3
  • 此时，慢跑者跑了 2 秒，总路程：2 步（2 秒 ×1 步 / 秒），停在节点 3。
  • 节点 3 恰好是 5 个节点的中间位置（第 3 个）。

场景 2：偶数个节点（n=6，节点 1→2→3→4→5→6）

• 跑道长度：6 个节点，终点在节点 6 右侧（NULL）。

• 快跑者（fast）的运动过程：

  • 初始位置：节点 1
  • 第 1 秒：跑 2 步→节点 3（1→2→3）
  • 第 2 秒：跑 2 步→节点 5（3→4→5）
  • 第 3 秒：跑 2 步→NULL（5→6→NULL）
  • 此时，快跑者到达 "终点"（NULL），停止运动。
  • 总运动时间：3 秒，总路程：6 步（3 秒 ×2 步 / 秒）。

• 慢跑者（slow）的运动过程：

  • 初始位置：节点 1
  • 第 1 秒：跑 1 步→节点 2
  • 第 2 秒：跑 1 步→节点 3
  • 第 3 秒：跑 1 步→节点 4
  • 此时，慢跑者跑了 3 秒，总路程：3 步（3 秒 ×1 步 / 秒），停在节点 4。
  • 节点 4 恰好是 6 个节点的 "第二个中间节点"（第 4 个）。

二、数学公式推导：用路程关系证明位置必然性

设：

• 链表总节点数为 n
• 慢指针速度 v_s = 1 步 / 次，快指针速度 v_f = 2 步 / 次
• 运动次数（循环次数）为 t（每次循环，两指针各移动一次）

1. 快指针的终止条件

快指针停止时，有两种情况：

• 奇数 n ：快指针在最后一个节点（fast->next = NULL），此时快指针走过的步数为 n-1（因为从节点 1 到节点 n 需要 n-1 步）。
• 偶数 n ：快指针在 NULL（fast = NULL），此时快指针走过的步数为 n（从节点 1 到 NULL 需要 n 步）。

两种情况可统一表示为：快指针走过的总步数 ≤ n 且 再走 2 步会越界。

2. 快慢指针的路程关系

由于运动时间相同（都是 t 次循环），路程 = 速度 × 时间：

• 快指针总路程：s_f = v_f × t = 2t
• 慢指针总路程：s_s = v_s × t = t

因此：s_s = s_f / 2（慢指针路程是快指针的一半）。

3. 代入 n 验证位置

• 当 n 为奇数（n=2k+1） ：

  快指针最终停在最后一个节点，总路程 s_f = 2k（因为 n-1=2k）。

  慢指针路程 s_s = 2k / 2 = k，即从 head 移动 k 步，到达第 k+1 个节点（中间节点）。

• 当 n 为偶数（n=2k） ：

  快指针最终停在 NULL，总路程 s_f = 2k。

  慢指针路程 s_s = 2k / 2 = k，即从 head 移动 k 步，到达第 k+1 个节点（第二个中间节点）。

而很显然，我们是需要while循环来进行循环，但是我们要设置什么样子的终止条件呢？首先可以确定的是和fast指针有关，因为fast肯定是会比slow指针更快到达链表尾部，即NULL，但是具体是什么呢？首先，对于偶数个节点，当slow指针运动到中间节点时，fast已经移动到了最后一个节点next指针上，即NULL，此时应该终止循环，即fast！=NULL，对于奇数个节点，当slow指针运动到中间节点时，fast已经移动到了最后一个节点next的next上了，即还是NULL，此时应该终止循环，即fast->next！=NULL,详细如下：

我们来逐行拆解循环条件 while (fast && fast->next) 的底层逻辑，结合具体场景分析为什么这个条件能完美避免越界，同时保证慢指针停在正确位置。

核心问题：快指针的 "2 步移动" 需要什么前提？

快指针每次要执行 fast = fast->next->next（移动 2 步），这个操作安全的前提是：

1. 当前 fast 不能是 NULL（否则无法访问 fast->next）；
2. fast->next 不能是 NULL（否则无法访问 fast->next->next）。

这两个前提缺一不可，否则会触发空指针访问错误（程序崩溃）。

条件 1：fast != NULL 的作用

防止快指针已经指向 NULL 时，继续执行 fast->next。

场景：偶数个节点（如 n=6，1→2→3→4→5→6）

• 当快指针移动到 NULL 前的最后一步：
  • 此时 fast 指向节点 5，fast->next 指向节点 6（非 NULL），满足循环条件，进入循环。
  • 执行 fast = fast->next->next → fast 从节点 5→6→NULL（现在 fast 是 NULL）。
• 下一次判断循环条件：
  • fast 是 NULL，fast && fast->next 结果为假，循环终止。
  • 若没有 fast != NULL 这个条件，会尝试访问 NULL->next，直接崩溃。

条件 2：fast->next != NULL 的作用

防止快指针指向最后一个节点 时，继续执行 fast->next->next。

场景：奇数个节点（如 n=5，1→2→3→4→5）

• 当快指针移动到最后一个节点前的一步：
  • 此时 fast 指向节点 3，fast->next 指向节点 4（非 NULL），满足循环条件，进入循环。
  • 执行 fast = fast->next->next → fast 从节点 3→4→5（现在 fast 指向最后一个节点 5）。
• 下一次判断循环条件：
  • fast 非 NULL，但 fast->next 是 NULL（节点 5 的 next 是 NULL），fast && fast->next 结果为假，循环终止。
  • 若没有 fast->next != NULL 这个条件，会尝试访问 节点5->next->next（即 NULL->next），直接崩溃。

循环条件的 "反向验证"：不满足时为什么安全？

当 while (fast && fast->next) 不成立时，有两种情况，且这两种情况都能保证慢指针在正确位置：

情况 1：fast == NULL（偶数节点）

• 说明快指针已跑到链表末尾（如 n=6 时，fast 最终是 NULL）。
• 此时慢指针移动了 n/2 步（如 n=6 时移动 3 步），恰好停在第 n/2 + 1 个节点（节点 4），符合 "返回第二个中间节点" 的要求。

情况 2：fast->next == NULL（奇数节点）

• 说明快指针停在最后一个节点（如 n=5 时，fast 指向节点 5）。
• 此时慢指针移动了 (n-1)/2 步（如 n=5 时移动 2 步），恰好停在第 (n+1)/2 个节点（节点 3），符合 "返回唯一中间节点" 的要求。

总结：循环条件的设计智慧

while (fast && fast->next) 看似简单，实则包含两层防护：

1. 防越界 ：确保快指针每次移动 2 步时，不会访问 NULL 的 next 指针，避免程序崩溃。
2. 精准终止：当循环终止时，无论链表是奇数还是偶数节点，慢指针的位置必然符合题目对 "中间节点" 的定义。

这个条件完美适配了快慢指针的速度差逻辑，是保证算法正确运行的核心保障。

而且在这里，我们要注意：

while(fast!=NULL&&fast->next!=NULL)，fast!=NULL&&fast->next!=NULL二者不可交换顺序，因为节点个数为偶数时，运行到最后时，fast为空了已经，那如果我们把fast->next!=NULL放在前面，那么程序就会先访问fast->next，会导致空指针访问 。

下面是方法二完整代码：

//快慢指针法

typedef struct ListNode sl;

struct ListNode* middleNode(struct ListNode* head) 
{
    sl* slow=head;
    sl* fast=head;
    while(fast!=NULL&&fast->next!=NULL)//二者不可交换顺序，因为节点个数为偶数时，运行到最后时，fast为空了已经，那如果我们把fast->next!=NULL放在前面，那么程序就会先访问fast->next，会导致空指针访问    
    {
        slow=slow->next;//slow移动一步
        fast=fast->next->next;//fast移动两步
    }
    return slow;
}

很简单，下面再给大家一个例子加深大家理解：

我们用两个具体的链表示例，逐步演示快慢指针法的执行过程，重点观察每次循环中指针的位置变化和循环条件的作用：

示例 1：奇数个节点链表（1->2->3->4->5）

链表结构：1 → 2 → 3 → 4 → 5 → NULL

初始状态：slow 和 fast 都指向节点 1

步骤 1：第一次循环判断

• 循环条件：fast != NULL（true，fast 指向 1）且 fast->next != NULL（true，1 的 next 是 2）
• 执行循环体：
  • slow = slow->next → slow 移动到节点 2
  • fast = fast->next->next → fast 从 1→2→3（移动到节点 3）

步骤 2：第二次循环判断

• 循环条件：fast != NULL（true，fast 指向 3）且 fast->next != NULL（true，3 的 next 是 4）
• 执行循环体：
  • slow = slow->next → slow 移动到节点 3
  • fast = fast->next->next → fast 从 3→4→5（移动到节点 5）

步骤 3：第三次循环判断

• 循环条件：fast != NULL（true，fast 指向 5）但 fast->next != NULL（false，5 的 next 是 NULL）
• 条件不成立，循环终止

最终结果

slow 指向节点 3（链表的中间节点），符合预期。

示例 2：偶数个节点链表（1->2->3->4->5->6）

链表结构：1 → 2 → 3 → 4 → 5 → 6 → NULL

初始状态：slow 和 fast 都指向节点 1

步骤 1：第一次循环判断

• 循环条件：fast != NULL（true）且 fast->next != NULL（true）
• 执行循环体：
  • slow 移动到节点 2
  • fast 移动到节点 3

步骤 2：第二次循环判断

• 循环条件：fast != NULL（true）且 fast->next != NULL（true）
• 执行循环体：
  • slow 移动到节点 3
  • fast 移动到节点 5

步骤 3：第三次循环判断

• 循环条件：fast != NULL（true）且 fast->next != NULL（true，5 的 next 是 6）
• 执行循环体：
  • slow 移动到节点 4
  • fast 移动到 NULL（从 5→6→NULL）

步骤 4：第四次循环判断

• 循环条件：fast != NULL（false，fast 已指向 NULL）
• 条件不成立，循环终止

最终结果

slow 指向节点 4（链表的第二个中间节点），符合预期。

关键细节：循环条件的顺序为什么不能交换？

如果写成 while (fast->next != NULL && fast != NULL)：

• 当 fast 已经是 NULL 时（如示例 2 的最终状态），会先执行 fast->next != NULL，导致访问 NULL->next，触发空指针错误。

原代码的 while (fast != NULL && fast->next != NULL) 利用了短路逻辑

• 若 fast 是 NULL，则不执行 fast->next != NULL，直接终止循环，避免崩溃

到此，两题的解析大功告成。

结语：

当你逐行看完这篇关于「反转链表」和「链表的中间节点」的解析时，或许你已经在草稿纸上画了无数次指针的轨迹，或许你曾为某个循环条件的细节反复推敲 ------ 但请相信，这份投入本身就是最珍贵的收获。

单链表这一数据结构，看似简单，却藏着编程世界最本质的逻辑。它没有数组的连续内存优势，全靠一个个指针 "牵线搭桥"，这种 "离散中见连续" 的特性，恰恰是锻炼逻辑思维的绝佳素材。就像我们在「反转链表」中看到的：无论是创建新链表时的 "头插重组"，还是三指针迭代时的 "原地转向"，核心都是通过改变指针的指向，让数据的流向彻底逆转。这过程中，每一步对 "下一个节点" 的提前保存（比如temp1或n3的作用），都是对 "链表断裂" 风险的预判 ------ 这种 "未雨绸缪" 的思维，正是编程能力的核心。

而「寻找中间节点」的两种方法，更像一场 "朴素与智慧" 的对话。计数法用两次遍历的 "实在"，让我们看清 "总长度与中间位置" 的直接关联；快慢指针法则用 "2 倍速度差" 的巧思，将两次遍历压缩为一次，用数学规律规避了对 "总长度" 的依赖。这两种思路没有优劣之分，却能让我们明白：解决问题的路径从来不止一条 ------ 有时需要 "笨办法" 打牢基础，有时需要 "巧思路" 提升效率。

我特别希望你能记住调试时的那些瞬间：当反转后的链表出现 "环"，你发现是忘记将原头节点的next置为NULL；当快慢指针越界，你才恍然大悟循环条件fast && fast->next的深层防护。这些错误不是绊脚石，而是帮你吃透细节的 "路标"。就像链表的节点需要next指针才能延续，我们对知识的理解也需要这些 "细节节点" 才能串联成体系。

或许你现在会觉得，"不就是反转和找中间吗？" 但请不要低估这些基础题目的价值。在实际开发中，链表的反转可能藏在 "逆序打印""链表深拷贝" 的需求里，中间节点的寻找可能是 "归并排序链表""判断链表是否有环" 的前置步骤。今天你在slow和fast指针上花的功夫，未来可能会在更复杂的算法中帮你节省数小时的调试时间。

编程的成长，从来不是 "学会多少题"，而是 "吃透多少逻辑"。当你能闭着眼睛在脑海中模拟出链表反转的每一步指针变化，能清晰解释为什么half = count / 2不需要加一，能瞬间判断fast和fast->next的循环条件顺序 ------ 你就已经掌握了 "透过现象看本质" 的能力。这种能力，会让你在面对更复杂的问题时，依然能抓住核心。

最后，想对你说：数据结构的学习就像链表本身，每一个知识点都是一个节点，看似孤立，实则环环相扣。今天你吃透了单链表的指针操作，明天面对二叉树的遍历、图的深度优先搜索时，会惊讶地发现：那些 "遍历""递归""指针跳转" 的逻辑，早已在单链表的练习中埋下了伏笔。

愿你在接下来的编程路上，既能像计数法一样踏实，一步一个脚印；也能像快慢指针一样灵活，于复杂中寻得巧思。如果某天你在面试或开发中遇到这两道题，希望你能想起今天画过的指针轨迹 ------ 那是你与数据结构对话的印记，也是你成长的见证。

下一道题，我们继续同行。