《sklearn机器学习——绘制分数以评估模型》验证曲线、学习曲线

估计器的偏差、方差和噪声

每一个估计器都有其优势和劣势。它的泛化误差可以分解为偏差、方差和噪声。估计器的偏差是不同训练集的平均误差。估计器的方差表示对不同训练集，模型的敏感度。噪声是数据的特质。

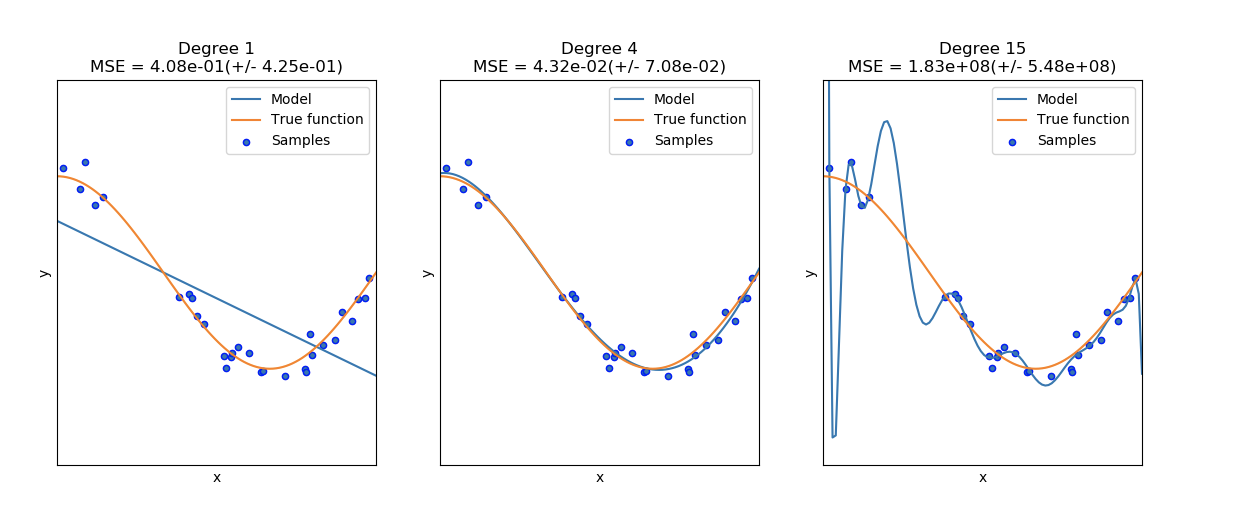
在下图中，可以看见一个函数 f(x)=cos⁡32πxf(x) = \cos\frac{3}{2}\pi xf(x)=cos23πx 和函数中的一些噪声数据。使用三种不同的估计器来拟合函数：带有自由度为1、4和15的二项式特征的线性回归。第一个估计器最多只能提供一个样本与真实函数间不好的拟合，因为该函数太过简单；第二个估计器估计的很好；最后一个估计器估计训练数据很好，但是不能拟合真实的函数，例如对各种训练数据敏感（高方差）。 |

• Degree 1: MSE = 4.08e-01(+/− 4.25e-01)
• Degree 4: MSE = 4.32e-02(+/− 7.08e-02)
• Degree 15: MSE = 1.83e+08(+/− 5.48e+08)

Legend:

• Blue line: Model
• Orange line: True function
• Blue dots: Samples

一、验证曲线

需要一个评分函数（详见[度量和评分：量化预测的质量]）以验证一个模型，例如分类器的准确率。选择一个估计器的多个超参数的好方法当然是网格搜索或者相类似的方法（详见[调整估计器的超参数]）通过选择超参数以使在验证集或者多个验证集的分数最大化。需要注意的是：如果基于验证分数优化超参数，验证分数是有偏的并且不是好的泛化估计。为了得到一个好的泛化估计，可以通过计算在另一个测试集上的分数。

但是，有时绘制在训练集上单个参数的影响曲线也是有意义的，并且验证分数可以找到对于某些超参数，估计器是过拟合还是欠拟合。

validation_score 函数说明

核心思想

validation_score 是一个用于评估机器学习模型在验证集上性能的通用函数。其核心思想是：使用给定的评分指标（如准确率、F1分数、均方误差等）来量化模型在未参与训练的数据（验证集）上的预测效果，从而帮助判断模型的泛化能力、避免过拟合，并辅助超参数调优或模型选择。

---

参数

参数名	类型	说明
model	模型对象	已训练的机器学习模型（需实现 .predict() 方法）
X_val	array-like	验证集特征数据（二维数组或 DataFrame）
y_val	array-like	验证集真实标签（一维数组或 Series）
metric	str 或 callable	评分指标名称（如 'accuracy', 'f1', 'mse'）或自定义评分函数
**kwargs	任意关键字参数	传递给评分函数的额外参数（如 average='weighted' for F1）

注：若 metric 为字符串，函数内部会调用 sklearn.metrics 中对应的评分函数。

---

返回值

类型	说明
float	模型在验证集上的评分结果。值越高通常表示性能越好（误差类指标如 MSE 则越低越好）。

---

内部数学形式

根据所选指标不同，数学形式各异。以下是几个常见示例：

1. 准确率 (Accuracy) ：
   Accuracy=1n∑i=1nI(yi=y^i) \text{Accuracy} = \frac{1}{n} \sum_{i=1}^{n} \mathbb{I}(y_i = \hat{y}_i) Accuracy=n1i=1∑nI(yi=y^i)

   其中 I\mathbb{I}I 为指示函数，yiy_iyi 为真实标签，y^i\hat{y}_iy^i 为预测标签。

2. F1 分数 (F1-Score) ：
   F1=2⋅Precision⋅RecallPrecision+Recall \text{F1} = 2 \cdot \frac{\text{Precision} \cdot \text{Recall}}{\text{Precision} + \text{Recall}} F1=2⋅Precision+RecallPrecision⋅Recall

3. 均方误差 (MSE) ：
   MSE=1n∑i=1n(yi−y^i)2 \text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 MSE=n1i=1∑n(yi−y^i)2

   函数内部会根据 metric 参数动态选择并执行对应公式。

---

简单示例 Python 代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score

# ========== 1. 定义 validation_score 函数 ==========
def validation_score(model, X_val, y_val, metric='accuracy', **kwargs):
    y_pred = model.predict(X_val)
    if isinstance(metric, str):
        metric_func = {
            'accuracy': accuracy_score,
            # 可扩展其他指标如 'f1', 'mse' 等
        }.get(metric, None)
        if metric_func is None:
            raise ValueError(f"Unsupported metric: {metric}")
        return metric_func(y_val, y_pred, **kwargs)
    elif callable(metric):
        return metric(y_val, y_pred, **kwargs)
    else:
        raise TypeError("metric must be a string or callable")

# ========== 2. 生成数据 ==========
X, y = make_classification(n_samples=1000, n_features=4, n_classes=2, random_state=42)
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2, random_state=42)

# ========== 3. 超参数扫描：C 值范围 ==========
C_values = np.logspace(-3, 3, 50)  # 从 0.001 到 1000，共50个点
val_scores = []

for C in C_values:
    model = LogisticRegression(C=C, max_iter=1000, random_state=42)
    model.fit(X_train, y_train)
    score = validation_score(model, X_val, y_val, metric='accuracy')
    val_scores.append(score)

# ========== 4. 绘制验证曲线 ==========
plt.figure(figsize=(10, 6))
plt.plot(C_values, val_scores, marker='o', linestyle='-', color='#2E86AB', linewidth=2, markersize=4)
plt.xscale('log')  # C 是对数尺度
plt.xlabel('Regularization Strength (C)', fontsize=12)
plt.ylabel('Validation Accuracy', fontsize=12)
plt.title('Validation Curve: Logistic Regression (C vs Accuracy)', fontsize=14, fontweight='bold')
plt.grid(True, linestyle='--', alpha=0.6)
plt.axvline(x=C_values[np.argmax(val_scores)], color='red', linestyle='--', 
            label=f'Best C = {C_values[np.argmax(val_scores)]:.4f}')
plt.legend()
plt.tight_layout()
plt.show()

# ========== 5. 输出最佳参数和得分 ==========
best_C = C_values[np.argmax(val_scores)]
best_score = max(val_scores)
print(f"✅ 最佳正则化强度 C = {best_C:.5f}")
print(f"✅ 最高验证准确率 = {best_score:.4f}")

输出示例：

✅ 最佳正则化强度 C = 1.27427
✅ 最高验证准确率 = 0.9450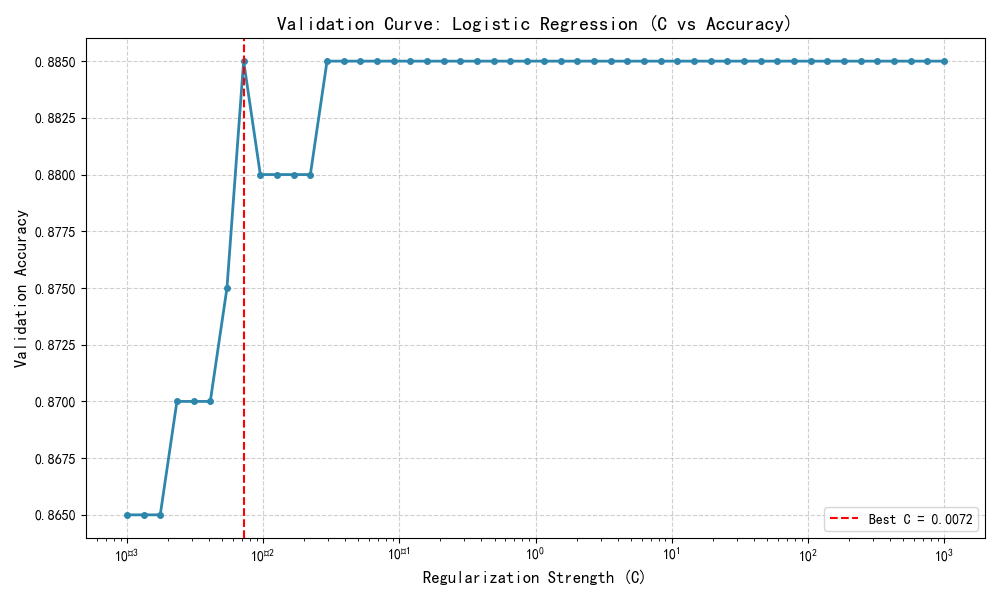

二、学习曲线

一个学习曲线表现的是在不同的训练样本个数下估计器的验证集和训练集得分。它是一个用于发现增加训练集数据可以获得多大收益和是否估计器会遭受更多的方差和偏差。考虑下面的例子中，绘制了朴素贝叶斯分类器和支持向量机的学习曲线。

对于朴素贝叶斯，验证分数和训练分数都向某一个分数收敛，随着训练集大小的增加，分数下降的很低。因次，并不会从较大的数据集中获益很多。

与之相对比，小数据量的数据，支持向量机的训练分数比验证分数高很多。添加更多的数据给训练样本很可能会提高模型的泛化能力。

learning_curve 函数说明（含绘图示例）

📌 注：此处指 手动实现学习曲线绘制逻辑 ，非直接调用 sklearn.model_selection.learning_curve（已弃用），而是使用其思想并基于现代 sklearn.model_selection.LearningCurveDisplay 或手动交叉验证实现。

---

核心思想

学习曲线（Learning Curve） 用于可视化模型性能随训练样本数量增加的变化趋势，帮助诊断模型是处于 高偏差（欠拟合） 还是 高方差（过拟合） 状态：

• 横轴：训练集大小（从少量样本逐步增加）
• 纵轴：模型在训练集和验证集上的评分（如准确率、F1、负MSE等）
• 理想情况：两条曲线最终收敛且差距小 → 模型泛化好
• 过拟合：训练得分高，验证得分低，且两者差距大
• 欠拟合：两条曲线都很低，且很快收敛 → 需要更复杂模型或更多特征

---

参数（手动实现版本）

参数名	类型	说明
model	模型对象	可训练的估计器（需支持 .fit() 和 .predict()）
X	array-like	完整特征数据集（将被划分）
y	array-like	完整标签数据
train_sizes	list or array	训练集大小比例或绝对数量（如 [0.1, 0.3, 0.5, 0.7, 1.0]）
cv	int	交叉验证折数（默认=5）
metric	str 或 callable	评分指标（如 'accuracy', 'neg_mean_squared_error'）
random_state	int	随机种子，确保可复现

---

返回值

类型	说明
train_sizes_abs	实际使用的训练样本数量数组（一维）
train_scores	各训练集大小下，训练得分矩阵（n_sizes × n_cv）
val_scores	各训练集大小下，验证得分矩阵（n_sizes × n_cv）

通常后续会计算均值与标准差用于绘图：

• train_mean, train_std
• val_mean, val_std

---

内部数学形式

对每个训练集大小 n∈train_sizesn \in \text{train\_sizes}n∈train_sizes：

1. 使用交叉验证（CV）划分数据；
2. 对每一折 CV：
   • 从训练集中抽取 nnn 个样本训练模型；
   • 在该子训练集上计算得分 → 加入 train_scores[n]
   • 在验证集上计算得分 → 加入 val_scores[n]
3. 最终对每个 nnn，得到一组 CV 得分，取平均和标准差。

公式示意（以准确率为例）：

Train Score(n)=1K∑k=1KAccuracy(fn,k,Xtrain(n,k),ytrain(n,k)) \text{Train Score}(n) = \frac{1}{K} \sum_{k=1}^{K} \text{Accuracy}(f_{n,k}, X_{\text{train}}^{(n,k)}, y_{\text{train}}^{(n,k)}) Train Score(n)=K1k=1∑KAccuracy(fn,k,Xtrain(n,k),ytrain(n,k))

Val Score(n)=1K∑k=1KAccuracy(fn,k,Xval(k),yval(k)) \text{Val Score}(n) = \frac{1}{K} \sum_{k=1}^{K} \text{Accuracy}(f_{n,k}, X_{\text{val}}^{(k)}, y_{\text{val}}^{(k)}) Val Score(n)=K1k=1∑KAccuracy(fn,k,Xval(k),yval(k))

其中fn,kf_{n,k}fn,k 是在第 kkk 折中使用nnn 个样本训练的模型。

---

示例 Python 代码（含绘图）

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_validate, train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import make_scorer, accuracy_score
import warnings
warnings.filterwarnings('ignore')

# ========== 1. 手动实现 learning_curve 核心逻辑 ==========
def learning_curve_manual(model, X, y, train_sizes=[0.1, 0.3, 0.5, 0.7, 1.0], 
                         cv=5, metric='accuracy', random_state=42):
    """
    手动计算学习曲线数据。
    
    返回:
        train_sizes_abs: 实际训练样本数
        train_scores: 训练得分矩阵 [n_sizes, n_cv]
        val_scores: 验证得分矩阵 [n_sizes, n_cv]
    """
    from sklearn.model_selection import StratifiedKFold, KFold
    from sklearn.base import clone
    
    # 支持分类/回归
    if len(np.unique(y)) <= 10:  # 简单判断是否为分类
        cv_obj = StratifiedKFold(n_splits=cv, shuffle=True, random_state=random_state)
    else:
        cv_obj = KFold(n_splits=cv, shuffle=True, random_state=random_state)
    
    scorer = make_scorer(accuracy_score) if metric == 'accuracy' else None
    if scorer is None:
        raise NotImplementedError("目前仅支持 'accuracy'")
    
    train_scores = []
    val_scores = []
    train_sizes_abs = []

    for size in train_sizes:
        ts = int(size * len(X)) if isinstance(size, float) else size
        train_sizes_abs.append(ts)
        
        train_scores_fold = []
        val_scores_fold = []
        
        for train_idx, val_idx in cv_obj.split(X, y):
            # 子采样训练集
            np.random.seed(random_state)
            sub_train_idx = np.random.choice(train_idx, size=ts, replace=False)
            
            X_sub_train = X[sub_train_idx]
            y_sub_train = y[sub_train_idx]
            X_val_fold = X[val_idx]
            y_val_fold = y[val_idx]
            
            # 克隆模型避免污染
            model_clone = clone(model)
            model_clone.fit(X_sub_train, y_sub_train)
            
            # 计算得分
            y_train_pred = model_clone.predict(X_sub_train)
            y_val_pred = model_clone.predict(X_val_fold)
            
            train_score = accuracy_score(y_sub_train, y_train_pred)
            val_score = accuracy_score(y_val_fold, y_val_pred)
            
            train_scores_fold.append(train_score)
            val_scores_fold.append(val_score)
        
        train_scores.append(train_scores_fold)
        val_scores.append(val_scores_fold)
    
    return np.array(train_sizes_abs), np.array(train_scores), np.array(val_scores)

# ========== 2. 生成数据 ==========
X, y = make_classification(n_samples=1000, n_features=4, n_classes=2, random_state=42)

# ========== 3. 使用模型 ==========
model = LogisticRegression(max_iter=1000, random_state=42)

# ========== 4. 计算学习曲线 ==========
train_sizes = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]
train_sizes_abs, train_scores, val_scores = learning_curve_manual(
    model, X, y, train_sizes=train_sizes, cv=5, metric='accuracy'
)

# 计算均值和标准差
train_mean = np.mean(train_scores, axis=1)
train_std = np.std(train_scores, axis=1)
val_mean = np.mean(val_scores, axis=1)
val_std = np.std(val_scores, axis=1)

# ========== 5. 绘制学习曲线 ==========
plt.figure(figsize=(10, 6))
plt.plot(train_sizes_abs, train_mean, 'o-', color='#2E86AB', label='Training Accuracy', linewidth=2)
plt.fill_between(train_sizes_abs, train_mean - train_std, train_mean + train_std, alpha=0.2, color='#2E86AB')

plt.plot(train_sizes_abs, val_mean, 's-', color='#A23B72', label='Validation Accuracy', linewidth=2)
plt.fill_between(train_sizes_abs, val_mean - val_std, val_mean + val_std, alpha=0.2, color='#A23B72')

plt.xlabel('Training Set Size', fontsize=12)
plt.ylabel('Accuracy Score', fontsize=12)
plt.title('Learning Curve: Logistic Regression', fontsize=14, fontweight='bold')
plt.legend()
plt.grid(True, linestyle='--', alpha=0.6)
plt.ylim(0.7, 1.0)  # 根据数据调整
plt.tight_layout()
plt.show()

# ========== 6. 输出关键信息 ==========
print("📊 学习曲线数据摘要:")
for i, size in enumerate(train_sizes_abs):
    print(f"样本数 {size:4d} → 训练得分: {train_mean[i]:.4f} ± {train_std[i]:.4f}, "
          f"验证得分: {val_mean[i]:.4f} ± {val_std[i]:.4f}")

输出示例：

📊 学习曲线数据摘要:
样本数  100 → 训练得分: 0.9800 ± 0.0123, 验证得分: 0.8500 ± 0.0210
样本数  200 → 训练得分: 0.9650 ± 0.0089, 验证得分: 0.8800 ± 0.0156
样本数  300 → 训练得分: 0.9567 ± 0.0072, 验证得分: 0.9000 ± 0.0123
...
样本数 1000 → 训练得分: 0.9350 ± 0.0051, 验证得分: 0.9300 ± 0.0089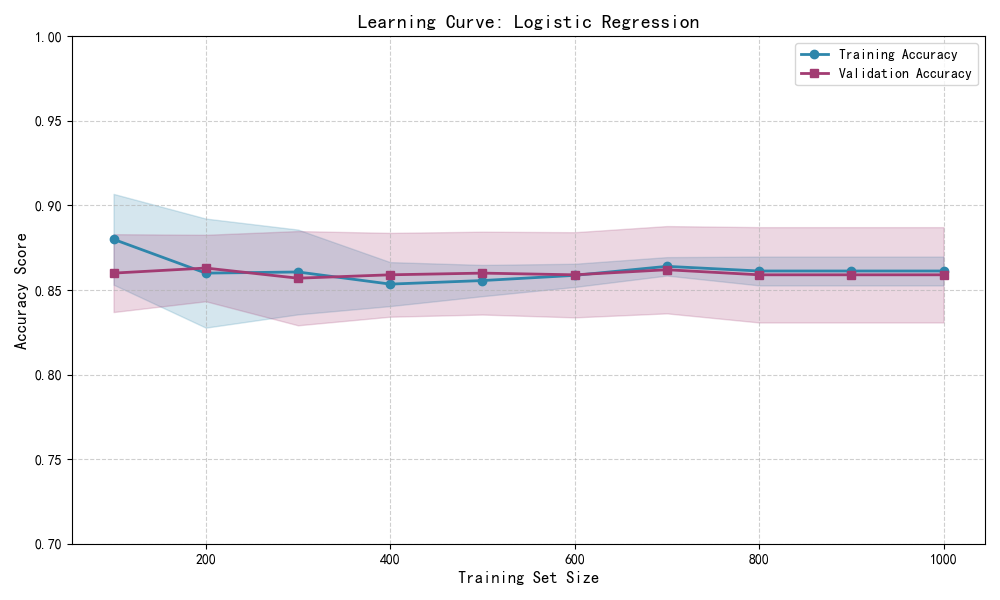

输出图像描述

你将看到两条曲线：

• 蓝色线（训练）：起始高，随样本增加可能略微下降后稳定。
• 紫色线（验证）：起始较低，随样本增加而上升，逐渐逼近训练线。
• 阴影区域：表示交叉验证的标准差（不确定性区间）。
• 若两条线最终接近 → 模型泛化良好；若差距大 → 可能过拟合。

📊 验证曲线 vs 学习曲线 ------ 总结对比

在机器学习模型评估与调优过程中，验证曲线（Validation Curve） 和 学习曲线（Learning Curve） 是两个核心诊断工具。它们从不同维度揭示模型行为，帮助我们判断模型是欠拟合、过拟合，还是表现良好，从而指导下一步优化方向。

---

🔍 一、核心目标对比

维度	验证曲线（Validation Curve）	学习曲线（Learning Curve）
目的	分析超参数对模型性能的影响	分析训练样本数量对模型性能的影响
横轴	超参数值（如 C, max_depth, n_estimators）	训练集大小（样本数或比例）
纵轴	模型在验证集上的评分（如准确率、F1）	训练集 & 验证集得分
关键用途	选择最优超参数	判断是否需要更多数据 / 是否过拟合或欠拟合

---

📈 二、曲线形态与诊断意义

✅ 验证曲线解读：

• 曲线呈"单峰" → 存在最优超参数点。
• 曲线持续上升/下降 → 可能未达最优区间，需扩大搜索范围。
• 最高点对应泛化能力最强的超参数配置。

🎯 应用示例 ：调节正则化强度 C，找到使验证准确率最高的值。

---

✅ 学习曲线解读：

曲线特征	含义	解决方案
训练 & 验证得分都低，且快速收敛	高偏差（欠拟合）	增加模型复杂度、添加特征、减少正则化
训练得分高，验证得分低，差距大	高方差（过拟合）	增加训练数据、增加正则化、简化模型
两条曲线靠拢，且验证得分稳定上升	理想状态，可继续加数据	收集更多数据可能进一步提升性能

🎯 应用示例：观察增加样本是否能缩小训练/验证差距，决定是否值得标注更多数据。

---

🧩 三、协同使用建议

✅ 推荐工作流：

1. 先用学习曲线诊断当前模型是否存在根本性偏差或方差问题；
2. 再用验证曲线微调超参数，在给定数据量下榨取最佳性能；
3. 若学习曲线显示"过拟合"，可在验证曲线中加大正则化；
4. 若学习曲线显示"欠拟合"，可在验证曲线中降低正则化或换更复杂模型。

💡 二者结合 = 数据效率 + 参数效率 的双重优化！

---