【LeetCode热题100道笔记】二叉搜索树中第 K 小的元素

题目描述

给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k 小的元素（从 1 开始计数）。

示例 1：

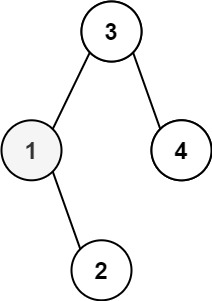
输入：root = [3,1,4,null,2], k = 1

输出：1

示例 2：

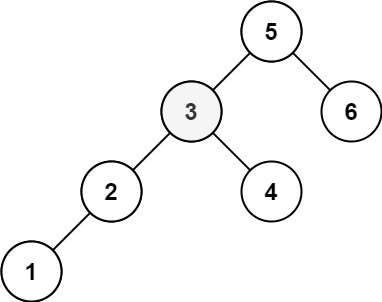
输入：root = [5,3,6,2,4,null,null,1], k = 3

输出：3

提示：

树中的节点数为 n 。
1<=k<=n<=1041 <= k <= n <= 10^41<=k<=n<=104
0<=Node.val<=1040 <= Node.val <= 10^40<=Node.val<=104

进阶：如果二叉搜索树经常被修改（插入/删除操作）并且你需要频繁地查找第 k 小的值，你将如何优化算法？

思考一：中序遍历（利用BST有序特性）

核心是借助BST中序遍历的有序性 ：中序遍历（左→根→右）会生成严格递增的节点值序列，序列中第k-1个元素（索引从0开始）即为第k小元素。

算法过程

1. 中序遍历收集节点值 ：
   • 初始化空数组arr，用于存储中序遍历的节点值；
   • 递归执行中序遍历：先遍历左子树（确保更小的元素先入数组），再将当前节点值加入arr，最后遍历右子树；
   • 若节点为空，直接返回（递归终止条件）。
2. 提取第k小元素 ：
   • 遍历完成后，arr已按递增排序，返回arr[k-1]（第k个元素，索引为k-1）。

时空复杂度

• 时间复杂度 ：O(n)，n为二叉树节点总数。
  原因：中序遍历需遍历所有节点（最坏情况需收集全部节点值才能找到第k小），总操作次数与节点数线性相关。
• 空间复杂度 ：O(n)。
  原因：数组arr需存储所有节点值（最坏情况），递归调用栈需O(h)（h为树高），总空间由数组主导，为O(n)。

代码

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} k
 * @return {number}
 */
var kthSmallest = function(root, k) {
    const arr = [];
    inOrder(root, arr);
    return arr[k-1];
};

function inOrder(node, arr) {
    if (!node) return;
    inOrder(node.left, arr);
    arr.push(node.val);
    inOrder(node.right, arr);
}

思考二：最大堆（动态维护最小的k个元素）

核心是用容量为k的最大堆 动态筛选"当前遍历到的最小k个元素"：堆顶始终是这k个元素中的最大值，遍历完成后堆顶即为第k小元素（因比堆顶小的元素有k-1个，堆顶自然是第k小）。
注：JavaScript无内置堆，需实现简易最大堆（按值大小排序，堆顶为最大值）。

算法过程

1. 实现最大堆 ：
   • 堆初始化时固定容量为k，超过容量时自动弹出堆顶（最大值）；
   • 提供push（插入元素并调整堆结构）、front（获取堆顶元素）、size（获取堆元素个数）方法。
2. 深度优先遍历（DFS）树节点 ：
   • 遍历所有节点，对每个节点值：
     • 若堆中元素不足k个，直接入堆；
     • 若堆已满且当前节点值 < 堆顶（说明当前节点值是更小的元素，需替换堆顶），弹出堆顶后将当前节点值入堆；
3. 返回结果：遍历完成后，堆顶元素即为第k小元素。

时空复杂度

• 时间复杂度 ：O(n log k)，n为二叉树节点总数。
  原因：遍历所有节点需O(n)，每个节点入堆/出堆操作需O(log k)（堆的调整时间与堆容量k的对数相关），总时间为O(n log k)。
• 空间复杂度 ：O(k + h)，h为树高。
  原因：堆占用O(k)空间，DFS递归栈占用O(h)空间，总空间由堆主导（k远小于n时比中序遍历更优）。

代码

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} k
 * @return {number}
 */
var kthSmallest = function(root, k) {
    const priorityQueue = new MyMaxPriorityQueue(k);
    dfs(root, priorityQueue, k);
    return priorityQueue.front();    
};

function dfs(node, queue, k) {
    if (!node) return;
    if (queue.size() < k || queue.front() > node.val) {
        queue.push(node.val);
    }
    dfs(node.left, queue, k);
    dfs(node.right, queue, k);
}


class MyMaxPriorityQueue {

    constructor(capacity = 1000) {
        this._data = [];
        this._capacity = capacity;
        this._size = 0;
    }

    front() {
        return this._data[0];
    }

    push(num) {
        if (this._capacity === this._size) {
            this.pop();
        }
        this._data.push(num);
        this.swim();
        this._size++;
    }

    pop() {
        if (this._data.length === 0) return;
        [this._data[0], this._data[this._data.length-1]] = [this._data[this._data.length-1], this._data[0]];
        const item = this._data.pop();
        this.sink();
        this._size--;
        return item;
    }

    swim(index = this._data.length-1) {
        while (index > 0) {
            let pIndex = Math.floor((index-1)/2);
            if (this._data[index] > this._data[pIndex]) {
                [this._data[index], this._data[pIndex]] = [this._data[pIndex], this._data[index]];
                index = pIndex;
                continue;
            }
            break;
        }

    }

    sink(index = 0) {
        const n = this._data.length;
        while (true) {
            let left = 2 * index + 1;
            let right = left + 1;
            let biggest = index;

            if (left < n && this._data[left] > this._data[index]) {
                biggest = left;
            }
            if (right < n && this._data[right] > this._data[biggest]) {
                biggest = right;
            }

            if (biggest !== index) {
                [this._data[biggest], this._data[index]] = [this._data[index], this._data[biggest]];
                index = biggest;
                continue;
            }

            break;
        }
    }

    size() {
        return this._size;
    }

}