上一章: 机器学习08------集成学习
下一章: 机器学习10------降维与度量学习
机器学习实战项目: 【从 0 到 1 落地】机器学习实操项目目录:覆盖入门到进阶,大学生就业 / 竞赛必备
文章目录
一、聚类任务(无监督学习的核心)
聚类是无监督学习中最核心的任务之一,目标是将无标记样本集划分为若干不相交的"簇"(cluster),以揭示数据内在的分布结构。
(一)形式化描述
- 给定样本集 D = { x 1 , x 2 , . . . , x m } D = \{x_1, x_2, ..., x_m\} D={x1,x2,...,xm},每个样本 x i x_i xi为n维特征向量;
- 聚类算法将 D D D划分为 k k k个簇 { C 1 , C 2 , . . . , C k } \{C_1, C_2, ..., C_k\} {C1,C2,...,Ck},满足:
- 簇间不相交: C l ′ ∩ l ′ ≠ l C l = ∅ C_{l'} \cap_{l' \neq l} C_l = \emptyset Cl′∩l′=lCl=∅;
- 覆盖所有样本: D = ∪ l = 1 k C l D = \cup_{l=1}^k C_l D=∪l=1kCl;
- 簇标记向量 λ = { λ 1 ; λ 2 ; . . . ; λ m } \lambda = \{\lambda_1; \lambda_2; ...; \lambda_m\} λ={λ1;λ2;...;λm}表示样本所属簇( λ j ∈ { 1 , 2 , . . . , k } \lambda_j \in \{1, 2, ..., k\} λj∈{1,2,...,k},即 x j ∈ C λ j x_j \in C_{\lambda_j} xj∈Cλj)。

二、聚类性能度量(有效性指标)
性能度量用于评价聚类结果的优劣,核心是"簇内相似度高、簇间相似度低",分为外部指标和内部指标。
(一)外部指标(与参考模型比较)
- 定义:将聚类结果与"参考模型"(如人工标注的簇划分)比较,通过样本对的匹配情况计算。
- 关键参数 :
- a a a:同簇且参考模型中同簇的样本对数量;
- b b b:同簇但参考模型中不同簇的样本对数量;
- c c c:不同簇但参考模型中同簇的样本对数量;
- d d d:不同簇且参考模型中不同簇的样本对数量。
- 常用指标 :
- Jaccard系数(JC): J C = a a + b + c JC = \frac{a}{a + b + c} JC=a+b+ca;
- FM指数(FMI): F M I = a a + b ⋅ a a + c FMI = \sqrt{\frac{a}{a + b} \cdot \frac{a}{a + c}} FMI=a+ba⋅a+ca ;
- Rand指数(RI): R I = 2 ( a + d ) m ( m − 1 ) RI = \frac{2(a + d)}{m(m - 1)} RI=m(m−1)2(a+d)。
(二)内部指标(直接评价聚类结果)
- 定义:基于聚类结果自身的统计特性(如距离、密度)评价,无需参考模型。
- 关键参数 :
- a v g ( C ) avg(C) avg(C):簇 C C C内样本平均距离;
- d i a m ( C ) diam(C) diam(C):簇 C C C内样本最大距离;
- d m i n ( C i , C j ) d_{min}(C_i, C_j) dmin(Ci,Cj):簇 C i C_i Ci与 C j C_j Cj的最近样本距离;
- d c e n ( C i , C j ) d_{cen}(C_i, C_j) dcen(Ci,Cj):簇 C i C_i Ci与 C j C_j Cj的中心距离。
- 常用指标 :
- DB指数(DBI): D B I = 1 k ∑ i = 1 k m a x j ≠ i ( a v g ( C i ) + a v g ( C j ) d c e n ( μ i , μ j ) ) DBI = \frac{1}{k} \sum_{i=1}^k max_{j \neq i} \left( \frac{avg(C_i) + avg(C_j)}{d_{cen}(\mu_i, \mu_j)} \right) DBI=k1∑i=1kmaxj=i(dcen(μi,μj)avg(Ci)+avg(Cj))(值越小越好);
- Dunn指数(DI): D I = m i n 1 ≤ i ≤ k { m i n j ≠ i ( d m i n ( C i , C j ) m a x 1 ≤ l ≤ k d i a m ( C l ) ) } DI = min_{1 \leq i \leq k} \left\{ min_{j \neq i} \left( \frac{d_{min}(C_i, C_j)}{max_{1 \leq l \leq k} diam(C_l)} \right) \right\} DI=min1≤i≤k{minj=i(max1≤l≤kdiam(Cl)dmin(Ci,Cj))}(值越大越好)。
三、距离计算(聚类的基础)
距离度量是聚类的核心,需满足非负性、同一性、对称性和直递性,不同属性类型需采用不同度量方式。
(一)常用距离
- 闵可夫斯基距离 : d i s t ( x i , x j ) = ( ∑ u = 1 n ∣ x i u − x j u ∣ p ) 1 / p dist(x_i, x_j) = \left( \sum_{u=1}^n |x_{iu} - x_{ju}|^p \right)^{1/p} dist(xi,xj)=(∑u=1n∣xiu−xju∣p)1/p,其中:
- p = 2 p=2 p=2为欧氏距离(最常用);
- p = 1 p=1 p=1为曼哈顿距离。
(二)属性类型与距离度量
- 连续属性:直接使用闵可夫斯基距离;
- 离散属性 :
- 有序属性:可转换为连续值后用闵可夫斯基距离;
- 无序属性:用VDM距离 :
V D M p ( a , b ) = ∑ i = 1 k ∣ m u , a , i m u , a − m u , b , i m u , b ∣ p VDM_p(a, b) = \sum_{i=1}^k \left| \frac{m_{u,a,i}}{m_{u,a}} - \frac{m_{u,b,i}}{m_{u,b}} \right|^p VDMp(a,b)=i=1∑k mu,amu,a,i−mu,bmu,b,i p
( m u , a , i m_{u,a,i} mu,a,i为第 i i i簇中属性 u u u取 a a a的样本数, m u , a m_{u,a} mu,a为属性 u u u取 a a a的总样本数);
- 混合属性 :结合闵可夫斯基距离和VDM:
M i n k o v D M p ( x i , x j ) = ( ∑ 连续属性 ∣ x i u − x j u ∣ p + ∑ 无序属性 V D M p ( x i u , x j u ) ) 1 / p MinkovDM_p(x_i, x_j) = \left( \sum_{连续属性} |x_{iu} - x_{ju}|^p + \sum_{无序属性} VDM_p(x_{iu}, x_{ju}) \right)^{1/p} MinkovDMp(xi,xj)=(连续属性∑∣xiu−xju∣p+无序属性∑VDMp(xiu,xju))1/p
四、原型聚类(基于原型的聚类)
原型聚类假设聚类结构可通过"原型"(如中心、概率分布)刻画,通过迭代优化原型实现聚类。
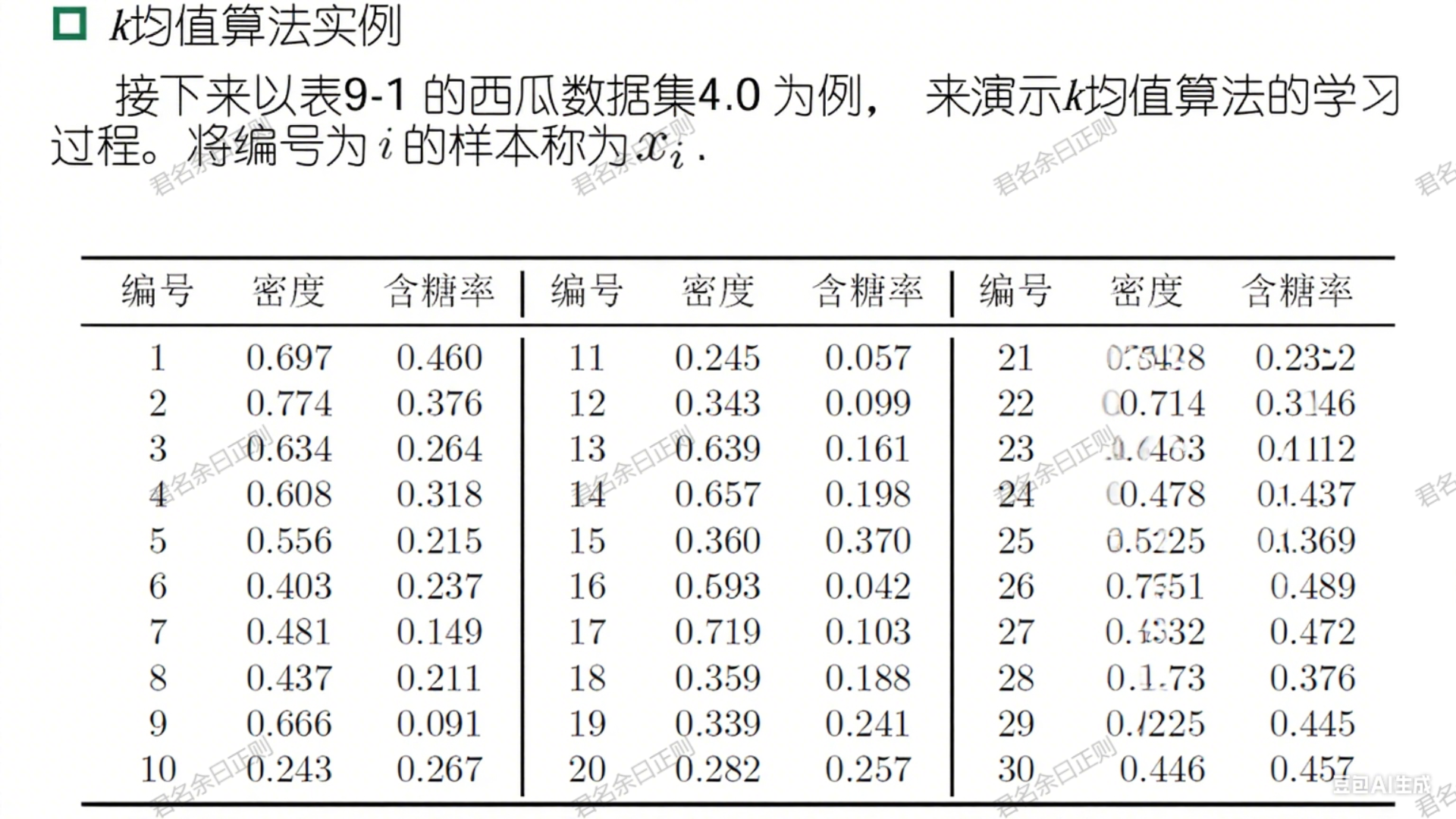
(一)k均值算法(k-means)
- 核心思想 :最小化簇内平方误差 E = ∑ i = 1 k ∑ x ∈ C i ∥ x − μ i ∥ 2 2 E = \sum_{i=1}^k \sum_{x \in C_i} \|x - \mu_i\|_2^2 E=∑i=1k∑x∈Ci∥x−μi∥22( μ i \mu_i μi为簇 C i C_i Ci的均值向量)。
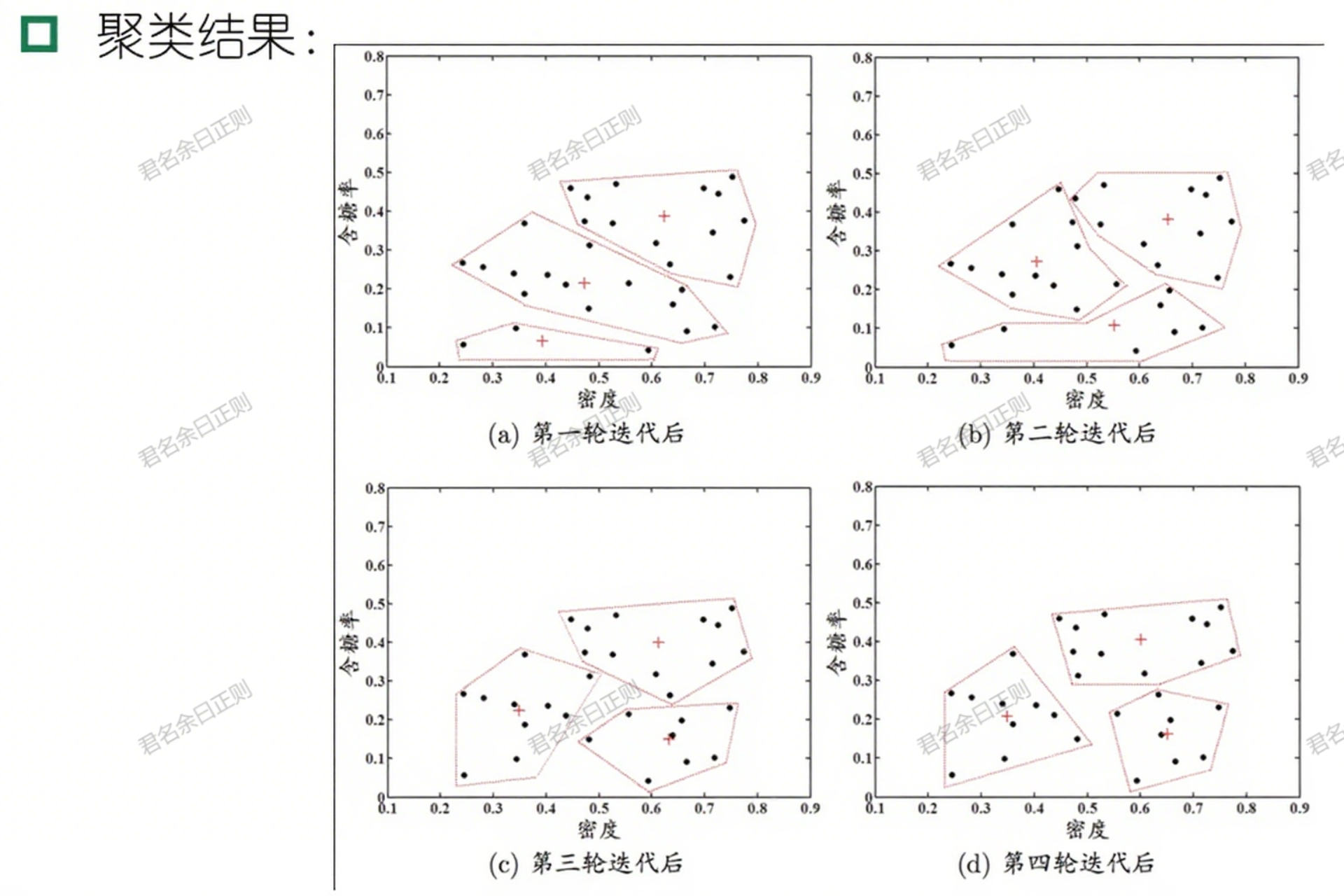
- 算法步骤 :
- 随机选择 k k k个样本作为初始均值向量 { μ 1 , μ 2 , . . . , μ k } \{\mu_1, \mu_2, ..., \mu_k\} {μ1,μ2,...,μk};
- 迭代:
- 簇划分:将每个样本划入距离最近的均值向量对应的簇;
- 更新均值:计算每个簇的新均值向量 μ i = 1 ∣ C i ∣ ∑ x ∈ C i x \mu_i = \frac{1}{|C_i|} \sum_{x \in C_i} x μi=∣Ci∣1∑x∈Cix;
- 终止:均值向量不再更新时停止。
- 特点 :高效易实现,但对初始中心敏感,适用于凸形分布数据。

- 模型定义 :混合分布 p M ( x ) = ∑ i = 1 k α i p ( x ∣ μ i , Σ i ) p_M(x) = \sum_{i=1}^k \alpha_i p(x | \mu_i, \Sigma_i) pM(x)=∑i=1kαip(x∣μi,Σi),其中 α i \alpha_i αi为混合系数( ∑ α i = 1 \sum \alpha_i = 1 ∑αi=1), p ( x ∣ μ i , Σ i ) p(x | \mu_i, \Sigma_i) p(x∣μi,Σi)为第 i i i个高斯分布(均值 μ i \mu_i μi,协方差 Σ i \Sigma_i Σi)。
- 求解方法(EM算法) :
- 初始化参数 { α i , μ i , Σ i } \{\alpha_i, \mu_i, \Sigma_i\} {αi,μi,Σi};
- 迭代(E步→M步):
- E步:计算样本 x j x_j xj属于第 i i i个成分的后验概率 γ j i = α i p ( x j ∣ μ i , Σ i ) ∑ l = 1 k α l p ( x j ∣ μ l , Σ l ) \gamma_{ji} = \frac{\alpha_i p(x_j | \mu_i, \Sigma_i)}{\sum_{l=1}^k \alpha_l p(x_j | \mu_l, \Sigma_l)} γji=∑l=1kαlp(xj∣μl,Σl)αip(xj∣μi,Σi);
- M步:更新参数 α i = 1 m ∑ j γ j i \alpha_i = \frac{1}{m} \sum_j \gamma_{ji} αi=m1∑jγji, μ i = ∑ j γ j i x j ∑ j γ j i \mu_i = \frac{\sum_j \gamma_{ji} x_j}{\sum_j \gamma_{ji}} μi=∑jγji∑jγjixj, Σ i = ∑ j γ j i ( x j − μ i ) ( x j − μ i ) T ∑ j γ j i \Sigma_i = \frac{\sum_j \gamma_{ji}(x_j - \mu_i)(x_j - \mu_i)^T}{\sum_j \gamma_{ji}} Σi=∑jγji∑jγji(xj−μi)(xj−μi)T;
- 终止:似然函数收敛。
- 特点:灵活拟合复杂分布,可输出样本属于各簇的概率,但计算复杂度高。
五、层次聚类(树形结构聚类)
层次聚类通过逐层合并或拆分簇,形成树形聚类结构,分为自底向上(聚合)和自顶向下(分拆)策略。
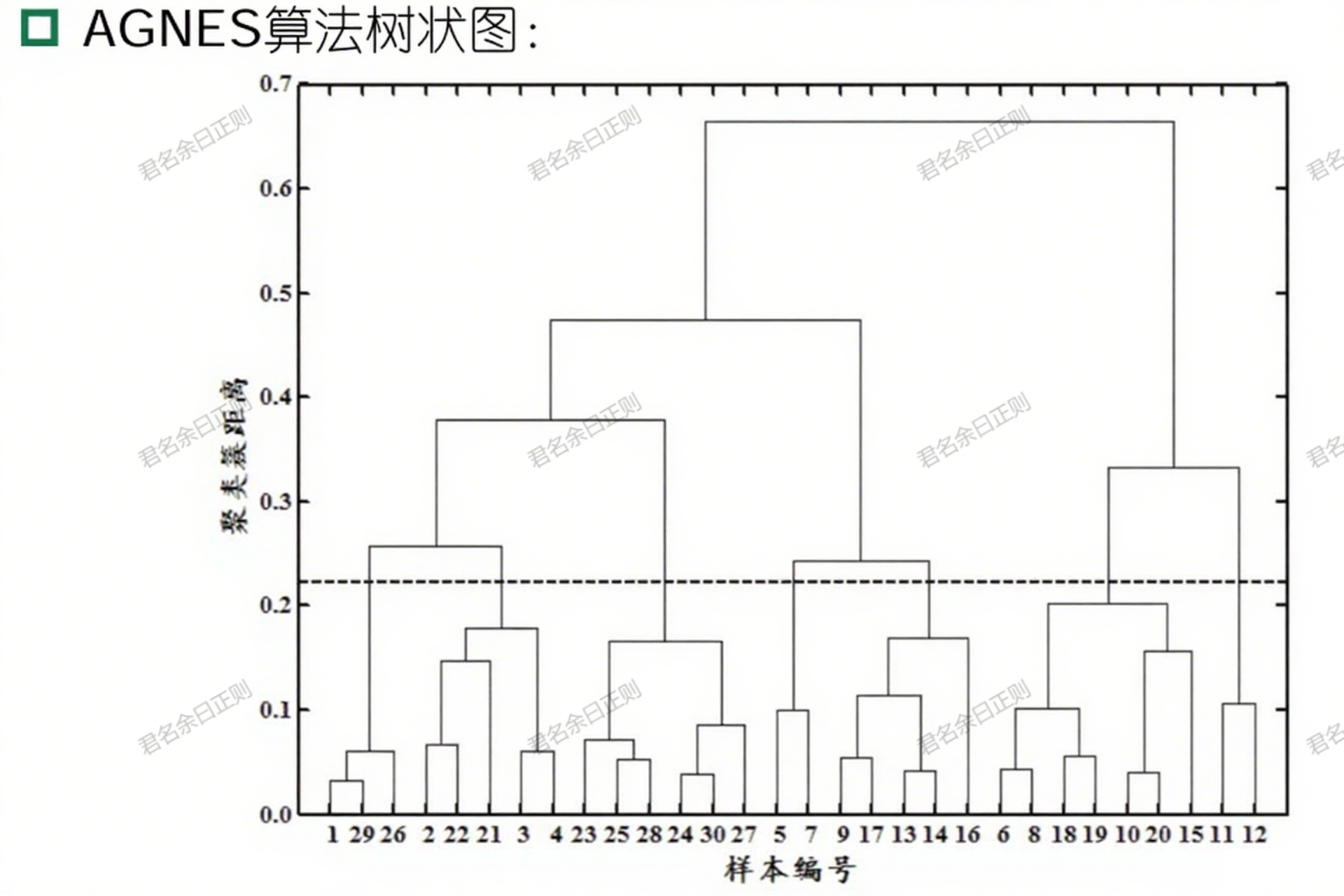
(一)AGNES算法(自底向上聚合)
- 核心思想 :初始将每个样本视为一个簇,迭代合并距离最近的两个簇,直至达到预设簇数 k k k。
- 簇距离度量 :
- 最小距离: d m i n ( C i , C j ) = m i n x ∈ C i , z ∈ C j d i s t ( x , z ) d_{min}(C_i, C_j) = min_{x \in C_i, z \in C_j} dist(x, z) dmin(Ci,Cj)=minx∈Ci,z∈Cjdist(x,z);
- 最大距离: d m a x ( C i , C j ) = m a x x ∈ C i , z ∈ C j d i s t ( x , z ) d_{max}(C_i, C_j) = max_{x \in C_i, z \in C_j} dist(x, z) dmax(Ci,Cj)=maxx∈Ci,z∈Cjdist(x,z);
- 平均距离: d a v g ( C i , C j ) = 1 ∣ C i ∣ ∣ C j ∣ ∑ x ∈ C i ∑ z ∈ C j d i s t ( x , z ) d_{avg}(C_i, C_j) = \frac{1}{|C_i||C_j|} \sum_{x \in C_i} \sum_{z \in C_j} dist(x, z) davg(Ci,Cj)=∣Ci∣∣Cj∣1∑x∈Ci∑z∈Cjdist(x,z)。
- 特点 :生成层次化簇结构,便于可视化,但计算复杂度高( O ( m 2 l o g m ) O(m^2 log m) O(m2logm)),对噪声敏感。
总结
聚类通过无监督方式揭示数据内在结构,性能可通过外部或内部指标评价。距离计算需根据属性类型选择(如连续属性用欧氏距离,无序属性用VDM)。原型聚类(k均值、高斯混合)高效且适用于大规模数据;层次聚类(AGNES)生成树形结构,适合探索数据层次关系。实际应用中需根据数据分布和任务需求选择算法。
上一章: 机器学习08------集成学习
下一章: 机器学习10------降维与度量学习
机器学习实战项目: 【从 0 到 1 落地】机器学习实操项目目录:覆盖入门到进阶,大学生就业 / 竞赛必备