🔥 本文专栏:c++
🌸作者主页:努力努力再努力wz



💪 今日博客励志语录 :
看似不起眼的日复一日,会在将来的某一天,突然让你看到坚持的意义
★★★ 本文前置知识:
unordered_set
引入
再之前的文章中,我介绍了set以及unordered_set,那么这两个容器的核心功能就是查找某个数据是否存在在该容器内,所以这两个容器可以应用于判断某个元素是否存在的场景
而本文要率先登场的数据结构:位图,那么它的应用场景和set以及unordered_set是一样的,也就是判断某个元素是否存在,那么它的原理是什么,以及和unordered_set和set有什么不同,那么我在后文都会将讲解,并且还会用代码来模拟实现一个位图,那么接下来就让我们进入位图的原理部分的讲解
位图
原理
根据上文,我们知道了位图的核心功能就是用来判断某个元素是否存在,那么存在与不存在这个两个状态我们可以用二进制的0和1来分别表示,0代表着不存在,而1代表着存在,而我们知道计算机中每一个比特位的值要么是0,要么是1,所以这里我们可以通过一个比特位的值来反映某个元素的存在情况
假设现在该程序会接收值在[Valmin,Valmax]范围上的元素,那么接收完在值在该范围上存在的所有元素之后,我们要判断值在[Valmin,Valmax]范围上的哪些元素出现过,那么首先我们得准备Valmax-Valmin+1个连续的比特位序列,那么这些比特位序列中的每一个比特位的初始值都是0,代表此时没有元素存在,那么每次接收一个元素,就需要我们计算出该元素对应的位索引,然后将该比特位设置为1即可
而查询某个特定值的元素是否存在,同样我们首先需要计算出该元素对应的位索引,然后确认该比特位的值是否为1,如果为1,那么意味着该元素存在
根据上面的过程,我们知道位图首先得准备一个连续的比特序列,也就是一个位图数组,但是所有的数据类型中,其单位最小的是char类型,其大小是一个字节,包含8个比特位,所以这里的位图数组,其实本质上是一个整形数组,可以是char类型的数组或者int以及long类型的数组,那么具体是什么类型的整形数组并不重要,因为这里位图数组中的每一个整形的作用,只是提供比特位,而我们并不关心数组中每一个元素的值,只关注数组中每一个元素中特定的比特位的值
那么假设我采取的是int类型的位图数组,那么int类型的数据大小是4个字节,包含32个比特位,如果该位图数组的长度为N,那么该位图数组总共能够提供数量为32*N个比特位,意味着能够表示32 * N个元素,而每一个比特位就会映射某个特定值的元素并且该比特位的值则意味着该元素是否存在
那么有了位图数组之后,下一步就是确定该元素值到位索引的映射,注意这里的映射关系,是元素值到位索引的映射,而不是数组索引的映射
那么这里我再来补充说明一下所谓的位索引:如果我们采取的是int类型的数组,我们知道每一个元素中的每一个比特位都能够映射对应值的元素,那么我们理解位图数组的时候,我们尽量把它想象或者理解为是由连续的比特位组成的数组,而不是连续的int类型的数据组成的数组,也就是将数组中连续的int类型的元素中的所有的比特位给拉直排列成一个整体的序列
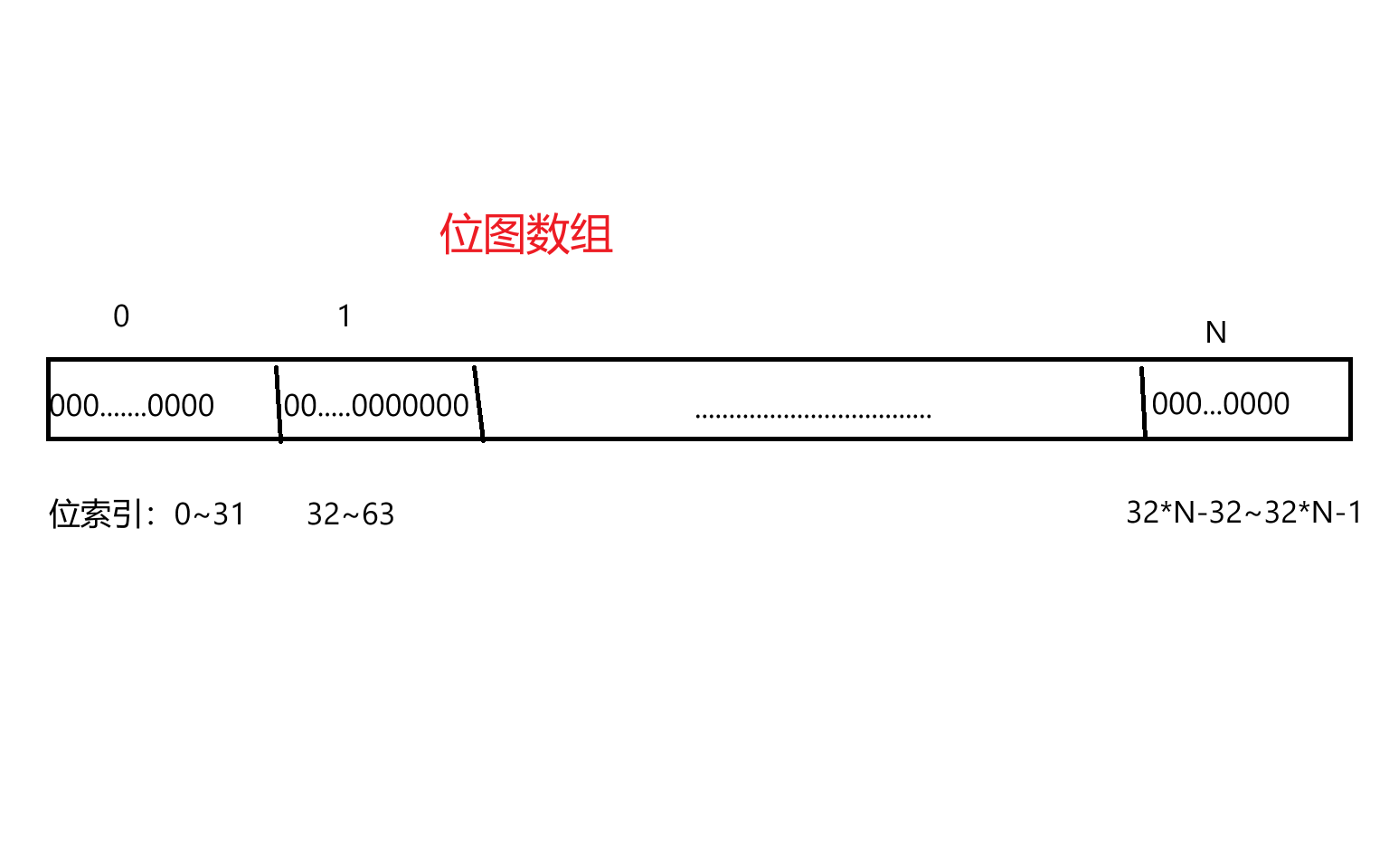
那么长度为N的int类型的位图数组,意味着就包含长度为32*N的比特位序列,那么这些比特位是从数组中的第一个元素的第一个比特位一直排列到数组中第N个元素的第32个比特位,那么每一个比特位都会对应一个唯一的从0开始连续递增的编号或者说下标,而某一个比特位的位索引则取决于他在这整个比特位的序列中的位置,比如他在第5个int类型的元素中的第3个比特位,那么它的位索引就是5 *32+2(下标是从0开始而不是从1来时,所以这里是加2而不是加三),而如果某一个比特位是位于第一个整形的第29个比特位中,那该比特位的位索引就是0 *32+28
所以这里创建完位图数组之后,下一步就是建立元素值与位图数组的位索引的映射,而这里的映射,指的就是哈希函数
如果该元素的类型是一个整形,对于整形元素来说,可以采取哈希函数有两种,首先是直接寻址法的哈希函数:
H a s h ( V a l ) = V a l − V a l m i n Hash(Val)=Val-Valmin Hash(Val)=Val−Valmin
那么该哈希函数计算得到的结果就是位索引,如果你要插入位图数组的元素值的范围为[Valmin,Valmax],那么值为Valmin的元素,则会映射到下标为0的比特位上
而采取该哈希函数的优势就是,该哈希函数是一个一次函数,根据一次函数的性质与图像,每一个自变量对应唯一的一个因变量,这里的自变量就是元素值,因变量就是位索引,意味着该哈希函数不会出现哈希碰撞,也就是不会出现不同的元素值会映射到同一个位索引的情况,那么每一个比特位的值就能精确的反应其对应的元素的状态,不会存在任何的误判
但是正是由于该哈希函数能够让位图数组的每一个比特位都能完全覆盖元素值的范围,所以这就要求我们在映射之前,一定要预先知道元素值的范围,从而给位图数组开辟一个能够完全覆盖元素值范围的数组长度,如果存在元素值的范围是[Valmin,Valmax],那么开辟的比特位的总长度就为Valmax-Valmin+1,然后再换算成数组的长度,这里如果是int类型,那么每一个int类型有32个比特位,那么这里就要开辟(Valmax-Valmin+1)/32+1长度的位图数组,这里后面加一的原因是因为这里的总长度不一定能够整除32,为了避免丢失最后的几个比特位,所以多开了一个元素,当然,如果刚好整除,那么就会浪费一个字节的空间,其实这一个字节浪费几乎可以忽略不计
而如果元素值Val映射的比特位下标超过了比特位的总长度,那么有的读者认为,如果出现这种情况,那么我们就直接扩容即可,然后将旧数组的元素依次拷贝到扩容后的新数组,然后再计算出该元素值对应的位索引,然后将该位索引对应的比特位设置为1即可
那么理论上这里确实没有任何问题,但是事实上,我们后面要模拟实现的标准库中提供的位图,其并没有没有扩容的机制,并且位图数组本身也不会采取动态数组,至于原因,就和我们后文讲的模拟实现有关,这里我先埋下一个伏笔
而这里还要注意的是,如果我们知道存在的元素的值的范围是[valmin,valmax],紧接着开辟好了位图数组,假设该范围很大,但是实际上我们插入位图数组的元素就只有几个,比如存在的元素值的范围为[0.1000000],但是我们插入位图的元素只有两个,分别为0和2,那么这里会导致位图数组的空间利用率低下,但是对于空间浪费来说,那么位图造成的影响几乎很少
因为不管位图数组中的每个元素的类型是long类型还是int类型,那么位图判断该元素是否存在,只需要存储一个比特位的信息,就能够反映该元素的状态,意味着每一个元素只会消耗一个比特位,而要知道1G等于1024MB,1Mb等于1024Kb,1Kb等于1024字节,1字节等于8个比特位,所以这里你要让位图造成大量的空间消耗或者空间浪费的话,那么意味着存在的元素值的范围得足够大,或者插入海量的数据,所以对于位图来说,唯一可能要注意的就是空间利用率的问题,反而对于位图来说,空间消耗则是最不用担心的问题
那么除了采取直接寻址法的哈希函数,那么这里还可以采取除留余数法的哈希函数:
Hash(val)=Val%N
这里的N注意是比特位的总长度而不是数组长度,那么除留余数法则不需要我们关心存在的元素的值的范围,因为不管元素值多大,那么代入该哈希函数得到的结果一定是[0,N-1],但是该哈希哈数的缺点就是会产生哈希碰撞,也就是不同的元素值会映射到同一个位索引,那么这就会导致误判,也就是如果元素值val1与元素值val2可能映射到同一个比特位,假设这里将元素val1插入到位图中,然后查询值为val2的元素是否存在,那么就会误判val2存在
而如果元素的类型不是整形,而是浮点型或者自定义类型,那么无法将浮点型或者自定义类型直接代入上文所说的哈希函数中,那么意味着这里需要二次映射
也就是得额外准备一个将浮点型或者自定义类型映射为整形的哈希函数,计算得到整形后,然后再将计算得到的整形代入上文提到的哈希函数中,最终得到位索引
模拟实现
而这里的模拟实现是标准库中实现的位图,也就是std::bitset,而根据上文的原理,我们知道将一个元素插入到位图当中,那么首先得开辟一定长度的位图数组,然后利用哈希函数计算出该元素值映射的位索引,然后将对应的比特位的值设置为1,那么这就是将已存在的元素插入到位图的一个原理
而对于查询来说,则是同样利用哈希函数计算出该元素值对应的位索引,然后查看该比特位的值是否为1
而有的读者很容易就误认为,标准库实现的位图是完成上面的所有环节,也就是创建数组,以及代入哈希函数计算出对应的位索引以及检查或者设置对应的比特位
但是事实上,标准库的位图并不会处理元素到位索引的映射,因为标准库中的biteset不像unordered_set,它不会内置哈希函数
所以将元素代入哈希函数计算得到对应的位索引则是由用户来负责完成,而标准库的biteset的核心的成员函数,比如set以及test,其只会接收位索引,然后将对应的比特位的值设置为1或者查询对应的比特位的值即可
所以这里就能解释上文所埋下的伏笔了,也就是为什么我们要实现的位图不存在扩容的机制,因为如果要扩容,如果你采取的是除留余数法的哈希函数,由于这里比特位的总长度变了,意味着你还得将之前插入的元素值重新映射,重新将元素值代入哈希函数位索引,但是问题是标准库中的位图并不会内置哈希函数,并且也不会保存你插入的元素值,所以这里无法完成重新映射的,所以不可能有扩容的机制存在,既然不需要扩容,那么底层也没必要维护一个动态数组,只需要维护一个静态数组即可,同时也避免了动态内存的开销

所以你会发现标准库的biteset会接收一个非类型的模版参数,其作用就是用来设置静态数组的长度,所以一旦你映射的比特位的下标超过了比特位的总长度,那么就会导致越界访问,不会存在扩容
所以接下来,我们实现的bitmap类,其会接收一个非类型模版参数,用来设置静态数组的大小,所以bitmap类还会封装一个静态数组,而这里我采取的静态数组的就是int类型的静态数组
cpp
template<size_t N>
class bitmap
{
public:
................
private:
int arr[N/32+1]={0}
}那么注意的就是这里的非类型模版参数是比特位的长度而不是数组的长度,那么这里需要将其转化为数组的长度,并且每一个元素都得初始化为0,因为初始状态没有插入任何元素,每一个比特位的值都应该是0
接着就是实现bitmap三个核心的成员函数,分别是set以及reset以及test
set
那么set函数的作用就是接收一个位索引,然后将该位索引对应的比特位的值设置为1,那么这里我们得判断位索引是否合法,合法后,再计算出该位索引是位于位图数组的哪个元素中,由于是int类型的位图数组,每一个元素包含32个比特位,所以这里我们直接除32,计算得到该比特位所在的元素的数组下标,假设下标为i
那么接下来就是计算该比特位在数组下标i的元素的一个偏移量,那么采取的就是模上32,得到该比特位下标是位于i个元素的第n个比特位上
那么接下来我们就得将第i个元素的第n个比特位的值设置为1,那么就要采取位运算,而根据或运算的规则:1I 1=1,1 | 0=1,所以这里对应的第n个比特位|= 1,那么会将该比特位的值设置为1,但注意这路只能修改第n个比特位的值,而不能修改其他比特位的值,所以这里我们就将值为1的数,将最低位的1左移n个单位长度到对应的比特位上,然后再与数组下标为i的数或等即可
cpp
void set(size_t pos)
{
assert(0 <= pos && pos <N);
size_t num = pos / 32;
size_t offset = pos % 32;
arr[num] |= (1<<offset);
}reset
rest函数的作用就是如果该比特位的值为1,就将其设置为0,那么其原理还是一样先判断位索引是否合法,然后再计算出该比特位 位与的整形的数组下标i,以及在该整形的偏移量
然后接着在进行位运算,而这里就要进行与运算,因为0&1=0,0&0 =0,那么这里为了不改变其他比特位的状态,所以这里要或的int类型的数,除了对应的比特位的值是0,其余都是1,因为1&1 =1,如果其他位置的比特位的值原本是1,那么与1与运算后的结果还是1,如果是0,那么与1与运算后的结果依然是0,所以这就要将值为1的数,将最低位的1左移n位,然后再按位取反,在与等 下标为i的数即可
cpp
void reset(size_t pos)
{
assert(0<=pos&&pos<N);
size_t num = pos / 32;
size_t offset = pos % 32;
arr[num] &= (~(1<<offset));
}Test
那么test函数就是检验对应的比特位的值是否为1,为1就返回true,反之,则返回false,那么这里还是检查位索引的合法性,然后再同样计算其位与第几个整形,以及在该整形的偏移量,然后再用值为1的数,将最低位的1给左移到对应的比特位,然后与对应的整形进行与运算,那么根据与运算的规则,1&1=1,0&1=0,那么将值为1的数左移之后,除了对应的比特位的值是1,其余都是0,所以如果与运算的结果非0,那么说明与运算的另一个数中对应的比特位的值为1,那么就返回true,而如果与运算的结果为0,说明与运算的另一个数中对应的比特位的值为0,则返回false
cpp
bool test(size_t pos)
{
assert(0<=pos&&pos<N);
size_t num = pos / 32;
size_t offset = pos % 32;
return arr[num] & (1<<offset);
}源码
bitmap.h:
cpp
#pragma once
namespace my_std {
template<size_t N>
class bitmap
{
public:
void set(size_t pos)
{
assert(0 <= pos && pos <N);
size_t num = pos / 32;
size_t offset = pos % 32;
arr[num] |= (1<<offset);
}
bool test(size_t pos)
{
assert(0<=pos&&pos<N);
size_t num = pos / 32;
size_t offset = pos % 32;
return arr[num] & (1<<offset);
}
void reset(size_t pos)
{
assert(0<=pos&&pos<N);
size_t num = pos / 32;
size_t offset = pos % 32;
arr[num] &= (~(1<<offset));
}
private:
int arr[N / 32 + 1] = { 0 };
};
}main.cpp:
cpp
#include <iostream>
#include <cassert>
#include "bitmap.h"
#include<bitset>
void test_bitmap() {
std::cout << "Starting bitmap tests..."<<std::endl;
// 测试1: 基本功能测试
{
my_std::bitmap<100> bm;
// 初始状态检查
for (size_t i = 0; i < 100; ++i) {
assert(!bm.test(i));
}
// 设置位并验证
bm.set(42);
assert(bm.test(42));
assert(!bm.test(41));
assert(!bm.test(43));
// 重置位并验证
bm.reset(42);
assert(!bm.test(42));
std::cout << "Test 1: Basic functionality passed"<<std::endl;
}
// 测试2: 边界测试
{
my_std::bitmap<64> bm;
// 测试第一个位
bm.set(0);
assert(bm.test(0));
bm.reset(0);
assert(!bm.test(0));
// 测试最后一个位
bm.set(63);
assert(bm.test(63));
bm.reset(63);
assert(!bm.test(63));
// 测试跨整数边界
bm.set(31); // 第一个整数的最后一位
bm.set(32); // 第二个整数的第一位
assert(bm.test(31));
assert(bm.test(32));
bm.reset(31);
bm.reset(32);
assert(!bm.test(31));
assert(!bm.test(32));
std::cout << "Test 2: Boundary conditions passed"<<std::endl;
}
// 测试3: 多位置位测试
{
my_std::bitmap<1000> bm;
// 设置所有位
for (size_t i = 0; i < 1000; ++i) {
bm.set(i);
}
// 验证所有位都被设置
for (size_t i = 0; i < 1000; ++i) {
assert(bm.test(i));
}
// 重置所有位
for (size_t i = 0; i < 1000; ++i) {
bm.reset(i);
}
// 验证所有位都被重置
for (size_t i = 0; i < 1000; ++i) {
assert(!bm.test(i));
}
std::cout << "Test 3: Multiple positions passed" << std::endl;
}
// 测试4: 性能测试
{
const size_t SIZE = 1000000; // 1百万位
my_std::bitmap<SIZE> bm;
// 测试设置速度
for (size_t i = 0; i < SIZE; i += 2) {
bm.set(i);
}
// 测试查询速度
for (size_t i = 0; i < SIZE; i += 3) {
bool exists = bm.test(i);
assert(exists == (i % 2 == 0));
}
std::cout << "Test 4: Performance test completed"<<std::endl;
}
std::cout << "All bitmap tests passed successfully!"<<std::endl;
}
int main() {
test_bitmap();
return 0;
}运行截图:
应用
那么知道了位图的原理以及模拟实现之后,那么我来说一下位图的应用场景,就是接收处理海量的数据,比如:这里我们要编写一个程序,其会接收40亿个字符串,每一个字符串的大小为100字节,然后统计字符串的种类有多少个
那么这里我们知道要统计字符串的种类,那么这40亿个字符串中,肯定有很多重复的字符串,所以这里要去重,那么有的读者自然就想到了使用set或者unordered_set这两个容器,将这40亿个字符串插入到set或者unordered_set中,然后再遍历一遍容器中存在的元素即可,但是这里总共40亿个字符串,每一个字符串的大小是100字节,那么总共就会消耗约为372G的空间,而内存总共就才4G或者8G,那么这里采取set或者unordered_set肯定是不可取的
而不可取的原因就是这里unorded_set以及set要存储整个字符串的内容,也就是完整的100字节,但对于位图来说,每一个字符串,位图只需存储一个比特位的信息即可,所以这里应该创建一个包含40亿个比特位的位图数组,然后利用哈希函数,得到每一个字符串对应的位索引,然后将该位索引对应的比特位设置为1,最后在遍历一遍位图即可,而40亿个比特,总共也就消耗500MB
那么这里位图唯一的缺点就是可能会存在哈希冲突,也就是误判,所以位图统计出来的字符串的种类数不精确
那么我再在刚才的场景中做一个变化,也就是编写一个程序,其会接收40亿个字符串,每一个字符串的大小是100字节,这里我们要统计出现次数为1次的字符串有多少个
而我们知道对于位图来说,那么每一个比特位要么为0,要么为1,只能表示对应的字符串存在或者不存在这两种状态,而这里要统计次数为1次的字符串,那么我们可以定义4种状态,分别是一次都没出现,只出现了一次,以及出现了两次和出现次数超过2次,那么这4种状态,就需要两个比特位来表示,分别是00,01,10,11
所以这里我们可以采取双位图,那么其中两个位图对应的比特位作为整体来判断,然后将存在的元素插入到双位图中
那么这里将元素插入到双位图的原理则是:首先将该元素代入哈希函数计算得到味索引,然后检查两个位图中该位索引对应的两个比特位,如果双位图的对应的两个比特位组合得到的结果为00,将其加一,变成01,也就是将第二个位图对应的比特位设置为1,而如果是01,就将第一个位图的比特位设置为1,第二个位图的比特位设置为0,后面以此类推
最后则是遍历双位图中每一个对应的比特位,统计01出现的次数即可
布隆过滤器
原理
那么上文我们介绍了位图,那么我们将对应的比特位下标设置为1之前,我们首先得将该元素代入哈希函数,计算得到位索引,而根据哈希函数的性质,哈希函数会发生哈希碰撞,导致不同的元素值映射到相同的位索引,那么这就会导致误判发生
而注意这里的误判一定是对元素的存在性造成误判,而对于某个元素的非存在性是不会造成任何的误判,因为如果检查某个元素是否存在,将该元素代入哈希函数计算得到对应的位索引,发现该位索引对应的比特位的值为0,意味着该元素一定是不存在的
但是如果值为1,意味着该元素是不一定存在,因为可能会有其他的元素也会映射到该比特位,将值设置为1
所以布隆过滤器便由此诞生了,布隆过滤器是由布隆发明的,那么布隆过滤器其实就是在位图的基础上进行了一个优化,那么布隆的思想就是降低位图的误判率,那么我们知道对于位图来说,那么每一个元素的状态只需要检查一个比特位,那么这一个比特位一旦产生冲突,那么就会导致误判
而布隆过滤器的思想很简单,那么就是判断一个元素是否存在,不再是检查一个比特位,而是让每一个元素映射到k个比特位,也就是代入k个独立的哈希函数,如果这k个比特位的值全部都为1,那么该元素才可以确认存在
要注意的是,即使每一个元素映射了k个比特位,但还是会存在误判的情况出现,因为这k个比特位一旦与其他元素的映射的比特位都有交集产生,那么同样也会造成误判,但是和只映射一个比特位相比,那么误判率肯定要低于只映射一个比特位的误判率
但布隆过滤器的缺点也很明显,那么它会造成位图的空间膨胀,因为每一个元素映射k个比特位,假设k为4,而这里数组的比特位个数为8的话,假设插入很多的元素到布隆过滤器的话,那么这里不会起到任何降低误判率的效果,所以需要较长的位图数组,那么位图数组越长,误判率肯定会越低,但是由于每一个元素只会消耗k个比特位,所以即使布隆过滤器造成了空间膨胀,那么对于空间的消耗来说,其实影响并不大
那么布隆过滤器的原理其实就这么简单,那么接下来的内容,就是关于模拟实现布隆过滤器
模拟实现
那么这里模拟实现布隆过滤器的话,那么布隆过滤器就要内置哈希函数,而由于要内置哈希函数,那么这里我们就无法灵活的设置哈希函数的个数,所以这里我采取的布隆过滤器,就是内置了三个哈希函数,也就是一个元素会映射三个比特位,而这里的哈希函数,则是对应一个()运算符重载函数,所以这里我们就得准备三个类,其中内部定义了()运算符重载函数,而这()运算符重载函数的内容正是对应的哈希函数的内容
而之后我们会将元素代入哈希函数计算,那么就通过创建一个仿函数对象,然后调用()运算符重载函数即可,所以这里我们得准备额外三个模版参数,分别会实例化三个带有()运算符重载函数的类,由于大部分映射的场景,都是针对的是字符串类型的映射场景,所以这三个模版参数,我都会提供一个缺省参数,这三个缺省参数都是内置的三个内容为字符哈希的()运算符重载函数的类
而这里的布隆过滤器本质上其实是一个位图,而根据上文,我们知道这里还得有一个非类型模版参数用来设置静态数组的长度,同时还需要一个模版参数用来被实例化元素的数据类型
cpp
class _HashFuc1
{
public:
size_t operator()(const std::string& key)
{
size_t hash = 0;
for (int i = 0;i < key.size();i++)
{
hash = hash * 131 + key[i];
}
return hash;
}
};
class _HashFuc2
{
public:
size_t operator()(const std::string& key)
{
size_t hash = 5381;
for (auto& c : key)
{
hash = ((hash << 5) + hash) + c; // hash * 33 + c
}
return hash;
}
};
class _HashFuc3
{
public:
size_t operator()(const std::string& key)
{
const uint32_t FNV_prime = 0x01000193; // 16777619
uint32_t hash = 0x811C9DC5; // 2166136261
for (auto& e : key)
{
hash ^= e;
hash *= FNV_prime;
}
return hash;
}
};
template<size_t N,typename T,typename HashFuc1=_HashFuc1,typename HashFuc2=_HashFuc2,typename HashFuc3=_HashFuc3>
class bloomfiter
{
private:
int arr[N / 32 + 1] = { 0 };
public:
.................
}set
那么这里的set和位图的set的原理是几乎一样,只不过要代入三个哈希函数计算出三个位索引,然后确定这三个位索引对应的比特位 位于哪一个整形中,以及在整形中的偏移量,然后再将这三个比特位的值都设置为1
cpp
void set(const T& key)
{
size_t hash1 = HashFuc1()(key) % N;
size_t num1 = hash1 / 32;
size_t offset1 = hash1 % 32;
size_t hash2 = HashFuc2()(key) % N;
size_t num2 = hash2 / 32;
size_t offset2 = hash2 % 32;
size_t hash3 = HashFuc3()(key) % N;
size_t num3 = hash3 / 32;
size_t offset3 = hash3 % 32;
arr[num1] |= (1<<offset1);
arr[num2] |= (1<<offset2);
arr[num3] |= (1 << offset3);
}test
test函数就是将该元素代入三个哈希函数,计算出映射的三个位索引,然后再计算这三个比特位 位与哪个整形以及在整形中的偏移量,最后检查三个比特位的值是否都为1,如果都为1,返回true,否则则返回false
cpp
bool test(const T& key)
{
size_t hash1 = HashFuc1()(key) % N;
size_t num1 = hash1 / 32;
size_t offset1 = hash1 % 32;
size_t hash2 = HashFuc2()(key) % N;
size_t num2 = hash2 / 32;
size_t offset2 = hash2 % 32;
size_t hash3 = HashFuc3()(key) % N;
size_t num3 = hash3 / 32;
size_t offset3 = hash3 % 32;
if ((arr[num1] & (1 << offset1)) && (arr[num2] & (1 << offset2)) && (arr[num3] & (1 << offset3)))
{
return true;
}
return false;
}要注意的是,这里布隆过滤器没有提供rest函数,因为rest函数是将该元素映射到的k个比特位的值都设置为0,而我们知道该元素映射到的k个比特位可能会与其他元素映射的比特位产生交集,如果这里将k个比特位设置为0,会影响其他元素的存在性,所以不能提供reset函数
源码
bloomfiter.h:
cpp
#pragma once
#include<string>
#include<cstdint>
class _HashFuc1
{
public:
size_t operator()(const std::string& key)
{
size_t hash = 0;
for (int i = 0;i < key.size();i++)
{
hash = hash * 131 + key[i];
}
return hash;
}
};
class _HashFuc2
{
public:
size_t operator()(const std::string& key)
{
size_t hash = 5381;
for (auto& c : key)
{
hash = ((hash << 5) + hash) + c; // hash * 33 + c
}
return hash;
}
};
class _HashFuc3
{
public:
size_t operator()(const std::string& key)
{
const uint32_t FNV_prime = 0x01000193; // 16777619
uint32_t hash = 0x811C9DC5; // 2166136261
for (auto& e : key)
{
hash ^= e;
hash *= FNV_prime;
}
return hash;
}
};
template<size_t N,typename T,typename HashFuc1=_HashFuc1,typename HashFuc2=_HashFuc2,typename HashFuc3=_HashFuc3>
class bloomfiter
{
private:
int arr[N / 32 + 1] = { 0 };
public:
void set(const T& key)
{
size_t hash1 = HashFuc1()(key) % N;
size_t num1 = hash1 / 32;
size_t offset1 = hash1 % 32;
size_t hash2 = HashFuc2()(key) % N;
size_t num2 = hash2 / 32;
size_t offset2 = hash2 % 32;
size_t hash3 = HashFuc3()(key) % N;
size_t num3 = hash3 / 32;
size_t offset3 = hash3 % 32;
arr[num1] |= (1<<offset1);
arr[num2] |= (1<<offset2);
arr[num3] |= (1 << offset3);
}
bool test(const T& key)
{
size_t hash1 = HashFuc1()(key) % N;
size_t num1 = hash1 / 32;
size_t offset1 = hash1 % 32;
size_t hash2 = HashFuc2()(key) % N;
size_t num2 = hash2 / 32;
size_t offset2 = hash2 % 32;
size_t hash3 = HashFuc3()(key) % N;
size_t num3 = hash3 / 32;
size_t offset3 = hash3 % 32;
if ((arr[num1] & (1 << offset1)) && (arr[num2] & (1 << offset2)) && (arr[num3] & (1 << offset3)))
{
return true;
}
return false;
}
};main.cpp:
cpp
#include <iostream>
#include <string>
#include <vector>
#include <cassert>
#include"bloomfiter.h"
int main() {
bloomfiter<1000, std::string> filter;
std::vector<std::string> testItems = {
"apple", "banana", "cherry", "date", "elderberry",
"fig", "grape", "honeydew", "kiwi", "lemon"
};
std::vector<std::string> nonExistentItems = {
"mango", "orange", "peach", "pear", "pineapple",
"plum", "raspberry", "strawberry", "watermelon"
};
std::cout << "test1:" << std::endl;
for (const auto& item : testItems) {
filter.set(item);
std::cout << "add: " << item << std::endl;
}
for (const auto& item : testItems) {
bool exists = filter.test(item);
std::cout << "check: " << item << " -> " << (exists ? "exist" : "not exist") << std::endl;
assert(exists && "added element should exist?");
}
std::cout << "test1 pass!" << std::endl << std::endl;
std::cout << "test2:" << std::endl;
int falsePositives = 0;
for (const auto& item : nonExistentItems) {
bool exists = filter.test(item);
std::cout << "check: " << item << " -> " << (exists ? "exist" : "not exist") << std::endl;
if (exists) {
falsePositives++;
std::cout << " ^^^ misjudge happend!" << std::endl;
}
}
std::cout << "misjudge nums: " << falsePositives << "/" << nonExistentItems.size() << std::endl;;
std::cout << "test2 pass!" << std::endl << std::endl;
std::cout << "Test3:" << std::endl;
filter.set("new_item");
for (const auto& item : testItems) {
bool exists = filter.test(item);
std::cout << "check: " << item << " -> " << (exists ? "exist" : "not exist") << std::endl;
assert(exists && "added element should exist?");
}
std::cout << "test3 pass!" << std::endl << std::endl;
std::cout << "test4 :" << std::endl;
filter.set("");
assert(filter.test("") && "empty string should exist");
std::cout << "empty srting test pass!" << std::endl;
std::string longStr(1000, 'a');
filter.set(longStr);
assert(filter.test(longStr) && "long string should exist");
std::cout << "long string test pass!" << std::endl;
std::string specialChars = "!@#$%^&*()_+-=[]{}";
filter.set(specialChars);
assert(filter.test(specialChars) && "special character should exist");
std::cout << "special string test pass" << std::endl;
std::cout << "All tests pass!" << std::endl;
return 0;
}运行截图:
补充
那么有的数学家也对布隆过滤器进行了大量的实验以及测试,来验证布隆过滤器的误判率与哈希函数个数以及位图数组长度以及插入元素个数的关系,那么经过大量的测试,最终得到了该公式:
P ≈ (1 - e^(-k * n / m))^k
其中:
P:误判概率
m:位数组的大小(位数)
k:哈希函数的数量
n:已插入元素的个数
以及并且对于给定的m和n,使误判率最小的哈希函数个数公式:
k = (m / n) * ln(2)
应用
那么布隆过滤器的应用场景就是进行分流,比如:
在一个用户的程序的注册模块中,那么用户注册需要设置昵称,而该程序要求用户设置的昵称不能重复,而用户的昵称就是一个string类型的数据,而已经成功注册的用户的昵称则是存储在数据库中,那么我们可以直接访问数据库,拿着用户要注册的字符串去遍历,然后确定该字符串是否被注册过,但是一旦该程序正在注册的用户人数过多,那么数据库被频繁访问,会导致数据库的性能下降
所以这里在访问数据库之前,我们可以构建一个布隆过滤器,然后将已存在的用户昵称插入到布隆过滤器中,那么在访问数据库之前,会先访问布隆过滤器,然后判断该昵称是否被注册过,如果结果是没被注册过,那么就不需要访问数据库,因为我们知道布隆过滤器对于元素的不存在是没有误判的,而如果查询布隆过滤器,得到的结果是该元素被注册过,那么会存在误判,此时就需要访问数据库,确定该昵称是否真的存在,那么布隆过滤器就能够大大的减少访问数据库的请求
不存在 可能存在 不存在 存在 用户提交昵称 查询布隆过滤器 允许注册 查询数据库 允许注册 拒绝注册 将新昵称加入布隆过滤器
其次就是这里的昵称注册,如果不是严格要求精确的确认用户的昵称是否重复,而是能够容忍误判的话,那么这里甚至不需要访问数据库,直接访问布隆过滤器即可,那么底层的实现对用户是不透明的,意味着上层用户也不知道该昵称是否重复
结语
那么这就是本文关于位图以及布隆过滤器的全部内容了,那么下一期我将会更新关于C++11的内容,那么我会持续更新,希望你能够多多关注,如果本文对你有帮组的话,还请三连加关注哦,你的支持就是我创作的最大动力!
