基于 SciPy 的矩阵运算与线性代数应用详解

基于 SciPy 的矩阵运算与线性代数应用详解

在科学计算中，矩阵与线性代数是非常核心的工具。SciPy 提供了功能强大且高效的 scipy.linalg 模块，它建立在优化后的 BLAS 与 LAPACK 库之上。如果 SciPy 在构建时使用了 ATLAS、LAPACK 和 BLAS 库，就能发挥极快的线性代数运算能力。相比于 NumPy，scipy.linalg 更加专业，函数覆盖面更广，几乎囊括了 numpy.linalg 的全部功能，并额外提供了更多高级函数。

本文将系统介绍 scipy.linalg 的核心功能，结合数学公式、代码示例和可视化案例，让你更直观地理解其应用场景。

---

1. 为什么使用 scipy.linalg

• 更强大 ：包含 numpy.linalg 的全部功能，并提供额外扩展。
• 更高效：始终基于 BLAS/LAPACK 构建，速度通常更快，而 NumPy 并不保证一定包含。
• 统一接口：直接面向矩阵与向量，方便科研计算。

建议 ：除非有特殊理由避免引入 SciPy，一般优先使用 scipy.linalg，尤其是涉及大规模矩阵运算时。

---

2. 矩阵表示与基本区别

在 Python 中，矩阵主要由 NumPy 提供的数据结构表示：

• numpy.ndarray：二维数组，推荐使用的标准方式。
• numpy.matrix：矩阵类，虽然提供了一些便捷特性，但并不推荐，容易造成混淆。scipy.linalg 对这两种结构均兼容。

示例：

import numpy as np
from scipy import linalg

A = np.array([[1, 2], [3, 4]])
print(linalg.inv(A))  # 使用 ndarray

[[-2.   1. ]
[ 1.5 -0.5]]

这里 linalg.inv 返回矩阵的逆矩阵，逆矩阵是一个重要概念，满足 A−1⋅A=IA^{-1} \cdot A = IA−1⋅A=I，即乘以原矩阵得到单位矩阵。

---

3. 矩阵求逆 (Inverse)

数学原理：
A−1⋅A=I A^{-1} \cdot A = I A−1⋅A=I

其中 III 是单位矩阵。

在 SciPy 中实现：

import numpy as np
from scipy import linalg

# 定义矩阵
A = np.array([[1, 3, 5],
              [2, 5, 1],
              [2, 3, 8]])

# 计算逆矩阵和验证结果
A_inv = linalg.inv(A)
I_check = A.dot(A_inv)

# 打印原矩阵
print("原矩阵 A:")
print(A)

# 打印逆矩阵
print("\n逆矩阵 A^-1:")
print(A_inv)

# 验证 A·A^-1 是否接近单位矩阵
# 在计算机里用浮点数求逆时，A·A^-1 的结果往往不是完全精确的单位矩阵，而是与单位矩阵非常接近（存在微小的数值误差）
print("\nA·A^-1 的结果 (应接近单位矩阵 I):")
print(I_check)

原矩阵 A:
[[1 3 5]
[2 5 1]
[2 3 8]]

逆矩阵 A^-1:
[[-1.48  0.36  0.88]
[ 0.56  0.08 -0.36]
[ 0.16 -0.12  0.04]]

A·A^-1 的结果 (应接近单位矩阵 I):
[[ 1.00000000e+00 -1.11022302e-16 -5.55111512e-17]
[ 3.05311332e-16  1.00000000e+00  1.87350135e-16]
[ 2.22044605e-16 -1.11022302e-16  1.00000000e+00]]

注意：由于浮点数精度，A·A^-1 并非完全等于单位矩阵，但误差通常在 10−1610^{-16}10−16 级别，非常接近。

可视化说明 ：通过 matshow 可以直观显示矩阵元素及其逆矩阵的关系（将 AAA 和 A−1A^{-1}A−1 相乘，结果应接近单位矩阵）。

import matplotlib.pyplot as plt
import seaborn as sns

sns.set_theme(style="whitegrid", font="SimHei", rc={"axes.unicode_minus": False})

# 可视化函数
def plot_matrix(ax, mat, title):
    im = ax.imshow(mat, cmap="Blues")

    # 设置格子边框
    ax.set_xticks(np.arange(mat.shape[1]+1)-0.5, minor=True)
    ax.set_yticks(np.arange(mat.shape[0]+1)-0.5, minor=True)
    ax.grid(which="minor", linestyle='-', linewidth=1.5)
    ax.tick_params(which="minor", bottom=False, left=False)

    # 去掉主刻度
    ax.set_xticks([])
    ax.set_yticks([])

    # 标题
    ax.set_title(title, fontsize=12)

    # 获取归一化器
    norm = im.norm

    # 数值标注，根据背景深浅自动调整字体颜色
    for i in range(mat.shape[0]):
        for j in range(mat.shape[1]):
            value = mat[i, j]
            color = "white" if norm(value) > 0.5 else "black"
            ax.text(j, i, f"{value:.2f}",
                    ha="center", va="center", color=color, fontsize=10)

    # colorbar
    plt.colorbar(im, ax=ax, fraction=0.046)

# 绘制子图
fig, axes = plt.subplots(1, 3, figsize=(12, 4))
titles = ["矩阵 A", "逆矩阵 A^-1", "A·A^-1 ≈ I"]

for ax, mat, title in zip(axes, [A, A_inv, I_check], titles):
    plot_matrix(ax, mat, title)

plt.tight_layout()
plt.show()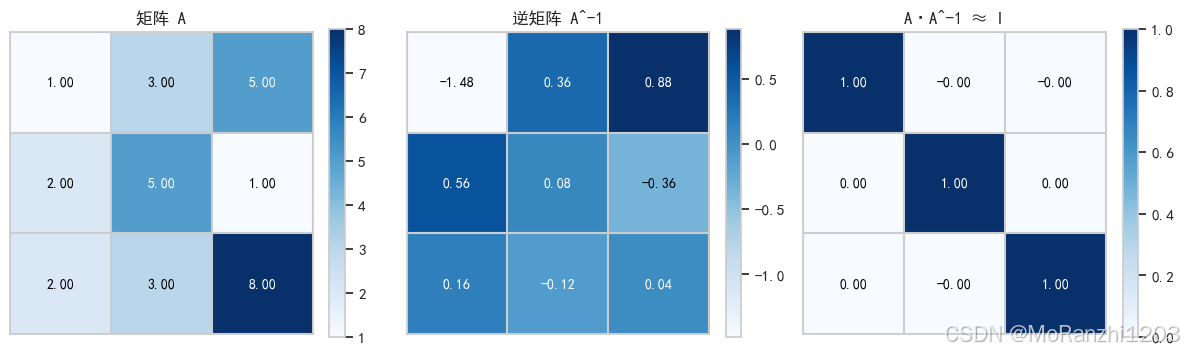

应用场景：解线性方程组、系统控制问题、数学建模中的逆运算。

---

4. 求解线性方程组 (Solve Linear Systems)

线性方程组形式：
A⋅x=b A \cdot x = b A⋅x=b

SciPy 提供 linalg.solve，比直接求逆再乘向量更高效、稳定：

# 数据
A = np.array([[1, 2],
              [3, 4]])
b = np.array([5, 6])
x = linalg.solve(A, b)

print("线性方程组的解 x 为：", x)

线性方程组的解 x 为：[-4.   4.5]

SciPy 提供 linalg.solve，比直接求逆再乘向量更高效、稳定：

结果显示两条直线相交于一点，这个交点就是方程组的唯一解。

from matplotlib.patches import FancyArrow, Polygon

x_vals = np.linspace(-5, 5, 400)
y1 = (5 - x_vals) / 2
y2 = (6 - 3 * x_vals) / 4

fig, ax = plt.subplots(figsize=(6, 6))

# 美化颜色和线条
line_colors = {"y1": "#1f77b4", "y2": "#ff7f0e"}  # 蓝色和橙色，柔和饱和
point_color = "#d62728"  # 红色点
sns.lineplot(x=x_vals, y=y1, ax=ax, color=line_colors["y1"], zorder=4, linewidth=2)
sns.lineplot(x=x_vals, y=y2, ax=ax, color=line_colors["y2"], zorder=4, linewidth=2)
sns.scatterplot(x=[x[0]], y=[x[1]], color=point_color, s=80, ax=ax, zorder=6)

# 生成透明白色蒙版
mask_radius = 0.5  # 蒙版半径
mask = Polygon([[x[0] - mask_radius, x[1] - mask_radius],
                [x[0] + mask_radius, x[1] - mask_radius],
                [x[0] + mask_radius, x[1] + mask_radius],
                [x[0] - mask_radius, x[1] + mask_radius]],
                closed=True, color="white", alpha=0.5, zorder=2)
ax.add_patch(mask)

# 整数刻度范围
xticks = np.arange(-5, 6, 1)
yticks = np.arange(-5, 6, 1)
ax.set_xticks(xticks)
ax.set_yticks(yticks)
ax.set_xlim(xticks[0]-0.5, xticks[-1]+0.5)
ax.set_ylim(yticks[0]-0.5, yticks[-1]+0.5)

# 网格
ax.set_axisbelow(True)
ax.grid(which="major", color="gray", linestyle="--", linewidth=0.5, alpha=0.5, zorder=0)

# 隐藏默认刻度数字
ax.set_xticklabels([])
ax.set_yticklabels([])

# 手动画刻度线
tick_len = 0.15
fontsize = plt.rcParams["xtick.labelsize"]

for xt in xticks:
    if xt == 0:
        continue
    ax.plot([xt, xt], [0, tick_len], color="black", lw=1, zorder=3)
    ax.text(xt, tick_len-0.25, str(int(xt)), ha="center", va="top", fontsize=fontsize, zorder=4)

for yt in yticks:
    if yt == 0:
        continue
    ax.plot([0, tick_len], [yt, yt], color="black", lw=1, zorder=3)
    ax.text(tick_len-0.25, yt, str(int(yt)), ha="right", va="center", fontsize=fontsize, zorder=4)

# 原点 "0"
zero_x = tick_len - 0.3
zero_y = tick_len - 0.25
ax.text(zero_x, zero_y, "0", ha="right", va="top", fontsize=fontsize, zorder=4)

# 坐标轴穿过原点
for spine in ["left", "bottom"]:
    ax.spines[spine].set_position("zero")
    ax.spines[spine].set_color("black")
for spine in ["top", "right"]:
    ax.spines[spine].set_color("none")

# 箭头
arrow_style = dict(width=0.02, head_width=0.25, head_length=0.3,
                   length_includes_head=True, color="black", linewidth=0.5)
xlim, ylim = ax.get_xlim(), ax.get_ylim()
ax.add_patch(FancyArrow(xlim[0], 0, xlim[1]-xlim[0], 0, **arrow_style, zorder=5))
ax.add_patch(FancyArrow(0, ylim[0], 0, ylim[1]-ylim[0], **arrow_style, zorder=5))

# 在函数线旁边添加标签
ax.text(1, 2.2, "x + 2y = 5", color=line_colors["y1"], fontsize=14, weight="bold")
ax.text(1.2, -1.8, "3x + 4y = 6", color=line_colors["y2"], fontsize=14, weight="bold")

# 生成透明白色蒙版
mask = Polygon([[x[0], x[1] - 0.7],
                [x[0] + 0.9, x[1] - 0.7],
                [x[0] + 0.9, x[1] - 0.1],
                [x[0], x[1] - 0.1]],
                closed=True, color="white", alpha=0.6, zorder=5)
ax.add_patch(mask)

# 原点解标注
ax.text(x[0]-1.1, x[1]-0.5, f"({x[0]:.1f},{x[1]:.1f})", color=point_color, fontsize=12, weight="bold", zorder=10)

# 解点投影到 x 轴
ax.plot([x[0], x[0]], [0, x[1]], color="gray", linestyle="--", linewidth=1, zorder=2)
# 解点投影到 y 轴
ax.plot([0, x[0]], [x[1], x[1]], color="gray", linestyle="--", linewidth=1, zorder=2)

# 标题
ax.set_title("线性方程组的几何解", fontsize=14, weight="bold")

plt.show()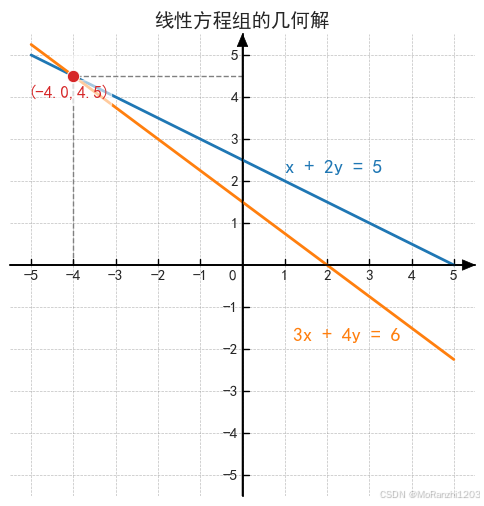

应用场景：物理建模、数据拟合、工程优化问题。

---

5. 行列式 (Determinant)

数学定义：
det⁡(A)=∑(−1)i+jaijMij \det(A) = \sum (-1)^{i+j} a_{ij} M_{ij} det(A)=∑(−1)i+jaijMij

行列式不仅用于判断矩阵是否可逆，还可用于几何解释，如二维矩阵作用下面积的缩放倍数。

示例：

A = np.array([[1, 2], [3, 1]])
det_A = linalg.det(A)
print("矩阵 A 的行列式为：", det_A)

矩阵 A 的行列式为： -5.0

可视化面积缩放：

# 定义单位正方形的顶点（顺时针或逆时针）
square = np.array([[0, 0],
                   [1, 0],
                   [1, 1],
                   [0, 1],
                   [0, 0]])  # 回到起点方便画图

# 矩阵作用到每个顶点上
transformed = square.dot(A.T)  # 注意 A.T 是因为我们是行向量表示顶点
print("单位正方形每个顶点经过矩阵 A 变换后的坐标：")
for i, point in enumerate(transformed):
    print(f"顶点 {i}: {point}")

单位正方形每个顶点经过矩阵 A 变换后的坐标：
顶点 0: [0 0]
顶点 1: [1 3]
顶点 2: [3 4]
顶点 3: [2 1]
顶点 4: [0 0]

# 绘制原单位正方形
plt.plot(square[:, 0], square[:, 1], "b--", linewidth=2)
for i, point in enumerate(square[:-1]):  # 最后一个点重复，已连接
    if i == 0:  # 只为第一个点标记 A(A')
        plt.text(point[0], point[1], "A(A')", color="black", fontsize=12, ha='right', va='center')
    elif i == 1:  # 对第一个变换后的点进行特定调整
        plt.text(point[0] + 0.05, point[1] , "B", color="black", fontsize=12, ha='left', va='center')
    elif i == 2:  # 对第二个变换后的点进行调整
        plt.text(point[0] + 0.05, point[1], "C", color="black", fontsize=12, ha='left', va='center')
    elif i == 3:  # 对第三个变换后的点进行调整
        plt.text(point[0] - 0.05, point[1], "D", color="black", fontsize=12, ha='right', va='center')

# 绘制变换后的平行四边形arrow_style
plt.plot(transformed[:, 0], transformed[:, 1], "r-", linewidth=2)
plt.fill(transformed[:, 0], transformed[:, 1], alpha=0.2, color="red")
for i, point in enumerate(transformed[:-1]):  # 最后一个点重复，已连接
    if i == 0:  # 不为第一个点显示文本
        continue
    # 定制每个顶点的标记
    elif i == 1:  # 对第一个变换后的点进行特定调整
        plt.text(point[0], point[1], "B'", color="black", fontsize=12, ha='right', va='bottom')
    elif i == 2:  # 对第二个变换后的点进行调整
        plt.text(point[0] + 0.05, point[1] + 0.1, "C'", color="black", fontsize=12, ha='left', va='top')
    elif i == 3:  # 对第三个变换后的点进行调整
        plt.text(point[0] + 0.1, point[1] - 0.05, "D'", color="black", fontsize=12, ha='left')

# 设置标题
plt.title(f"矩阵 A 作用下单位正方形的变换 (det(A) = {det_A:.2f})")
plt.axis("equal")
plt.show()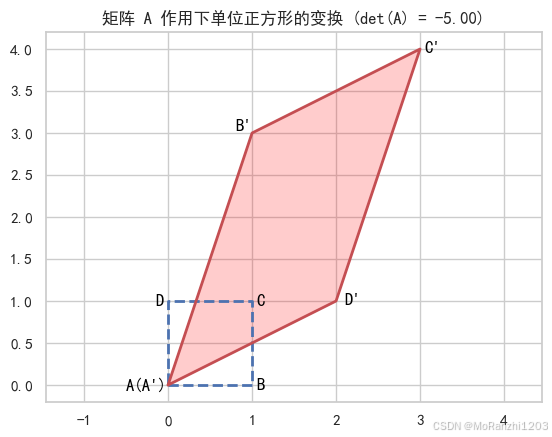

应用场景：矩阵可逆性判定、线性相关性分析、几何面积缩放。

---

6. 矩阵范数 (Norms)

矩阵范数是将矩阵映射为非负实数的函数，用于衡量矩阵的整体"大小"。

常用范数：

• Frobenius 范数：平方和开方，相当于二维向量的 L2 范数推广。
• L1 范数：各列元素绝对值之和最大值。
• L∞ 范数：各行元素绝对值之和最大值。

print("矩阵范数示例：")
A = np.array([[1, 2], [3, 4]])
print("矩阵 A =\n", A)
print("Frobenius 范数 ||A||_F =", linalg.norm(A))         # 默认 Frobenius 范数
print("L1 范数 ||A||_1 =", linalg.norm(A, 1))            # 列和范数
print("L∞ 范数 ||A||_inf =", linalg.norm(A, np.inf))     # 行和最大值

矩阵范数示例：
矩阵 A =
[[1 2]
[3 4]]
Frobenius 范数 ||A||_F = 5.477225575051661
L1 范数 ||A||_1 = 6.0
L∞ 范数 ||A||_inf = 7.0

可视化二维向量在不同范数下的单位圆/菱形/方形：

theta = np.linspace(0, 2*np.pi, 400)

# L2 范数单位圆
x2 = np.cos(theta)
y2 = np.sin(theta)

# L1 范数单位菱形
x1 = np.array([1, 0, -1, 0, 1])
y1 = np.array([0, 1, 0, -1, 0])

# L∞ 范数单位方形
x_inf = np.array([1, 1, -1, -1, 1])
y_inf = np.array([1, -1, -1, 1, 1])

plt.figure(figsize=(7,7))
plt.plot(x2, y2, label='Frobenius / L2', color='dodgerblue', linewidth=2)
# plt.fill(x2, y2, color='dodgerblue', alpha=0.1)

plt.plot(x1, y1, label='L1 范数', color='orange', linewidth=2)
# plt.fill(x1, y1, color='orange', alpha=0.1)
plt.scatter(x1[:-1], y1[:-1], color='orange')  # 顶点标记

plt.plot(x_inf, y_inf, label='L∞ 范数', color='green', linewidth=2)
# plt.fill(x_inf, y_inf, color='green', alpha=0.1)
plt.scatter(x_inf[:-1], y_inf[:-1], color='green')  # 顶点标记

plt.axis('equal')
plt.grid(True, linestyle='--', alpha=0.5)
plt.legend(fontsize=12)
plt.title("二维向量在不同范数下的单位球形状", fontsize=14)
plt.xlabel("x轴")
plt.ylabel("y轴")
plt.show()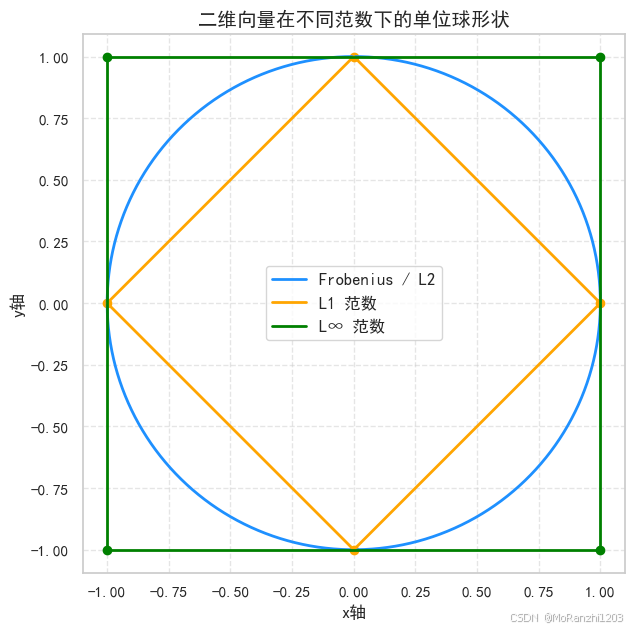

应用场景：优化问题中的正则化、误差分析、数值稳定性检查。

---

7. 总结与建议

• scipy.linalg 是科研计算中更推荐的线性代数库，相比 NumPy 更强大和高效。
• 核心功能包括：矩阵求逆、线性方程组求解、行列式计算、范数计算等。
• 建议配合 可视化 理解几何意义，例如交点、面积缩放、向量长度变化。

学习路径 ：从 inv 和 solve 入手，逐步扩展到 det、norm、特征值分解等高级方法。