目录
1.课题概述
CMAC(Cerebellar Model Articulation Controller,小脑模型关节控制器)神经网络是一种模仿人类小脑运动控制机制的局部逼近神经网络,具有学习速度快、泛化能力强、实时性高的特点。将其与传统PID控制器结合形成的复合控制器,既能利用PID对线性系统的稳定控制能力,又能通过CMAC补偿系统非线性、参数时变或外部扰动带来的控制偏差,广泛应用于机器人、工业过程控制、运动控制等领域。
2.系统仿真结果
3.核心程序
matlab2024b
% 调整时间
steady_state = sim_data.rin(end);
tolerance = 0.05 * steady_state;
stable_idx = find(abs(sim_data.yout - steady_state) <= tolerance, 1, 'first');
performance.settling_time = sim_data.time(stable_idx);
%% 6. 显示性能指标
fprintf('控制系统性能指标:\n');
fprintf('1. 稳态误差: %.6f\n', performance.steady_state_error);
fprintf('2. 均方误差(MSE): %.6f\n', performance.mse);
fprintf('3. 积分绝对误差(IAE): %.6f\n', performance.iae);
fprintf('4. 积分时间绝对误差(ITAE): %.6f\n', performance.itae);
fprintf('5. 超调量: %.2f%%\n', performance.overshoot);
fprintf('6. 上升时间: %.4f秒\n', performance.rise_time);
fprintf('7. 调整时间: %.4f秒\n', performance.settling_time);
%% 7. 结果可视化
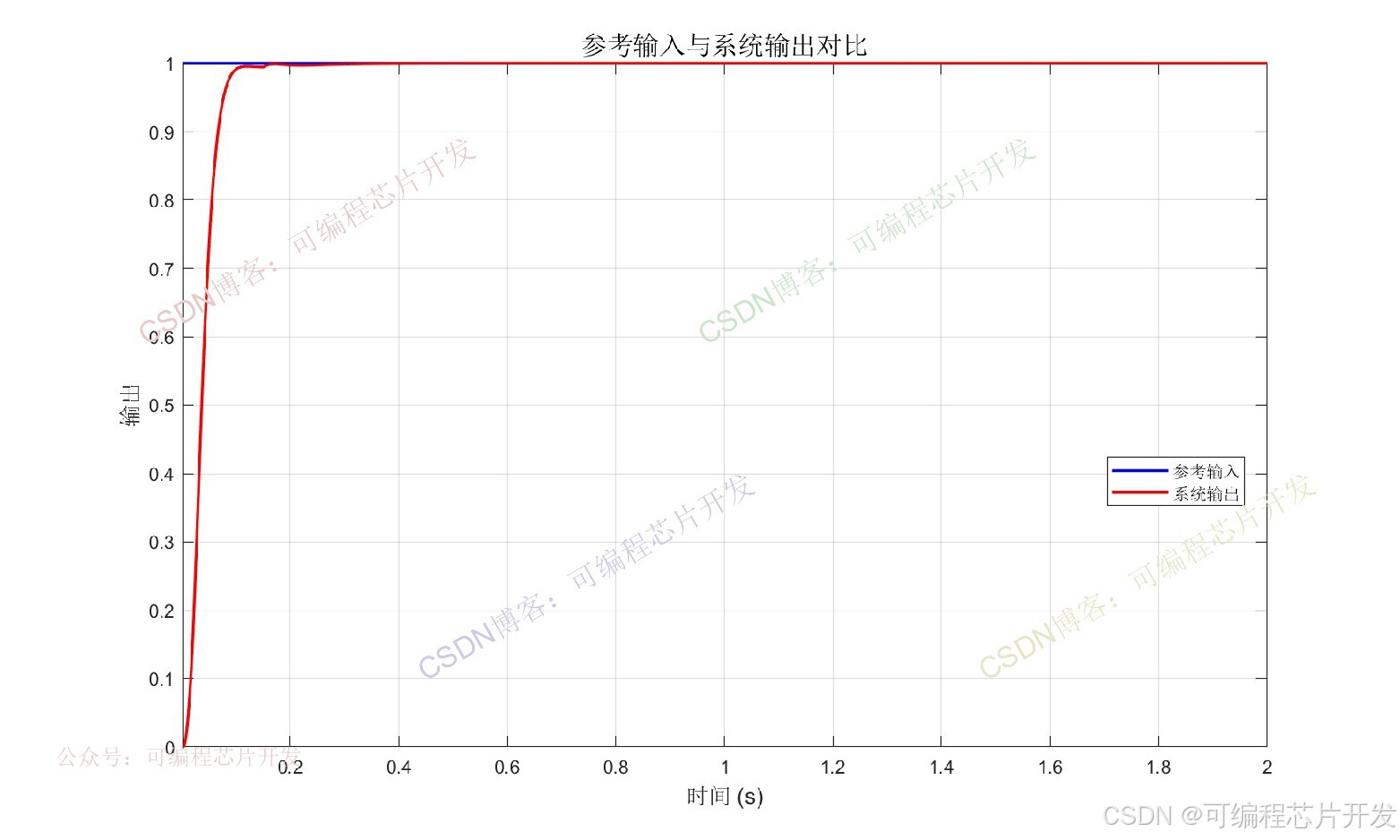
% 图1: 参考输入与系统输出
figure('Name', '系统跟踪性能', 'Position', [100, 100, 1000, 600]);
plot(sim_data.time, sim_data.rin, 'b-', 'LineWidth', 1.5);
hold on; grid on;
plot(sim_data.time, sim_data.yout, 'r-', 'LineWidth', 1.5);
xlabel('时间 (s)', 'FontSize', 12);
ylabel('输出', 'FontSize', 12);
title('参考输入与系统输出对比', 'FontSize', 14);
legend('参考输入', '系统输出', 'Location', 'Best');
axis tight;
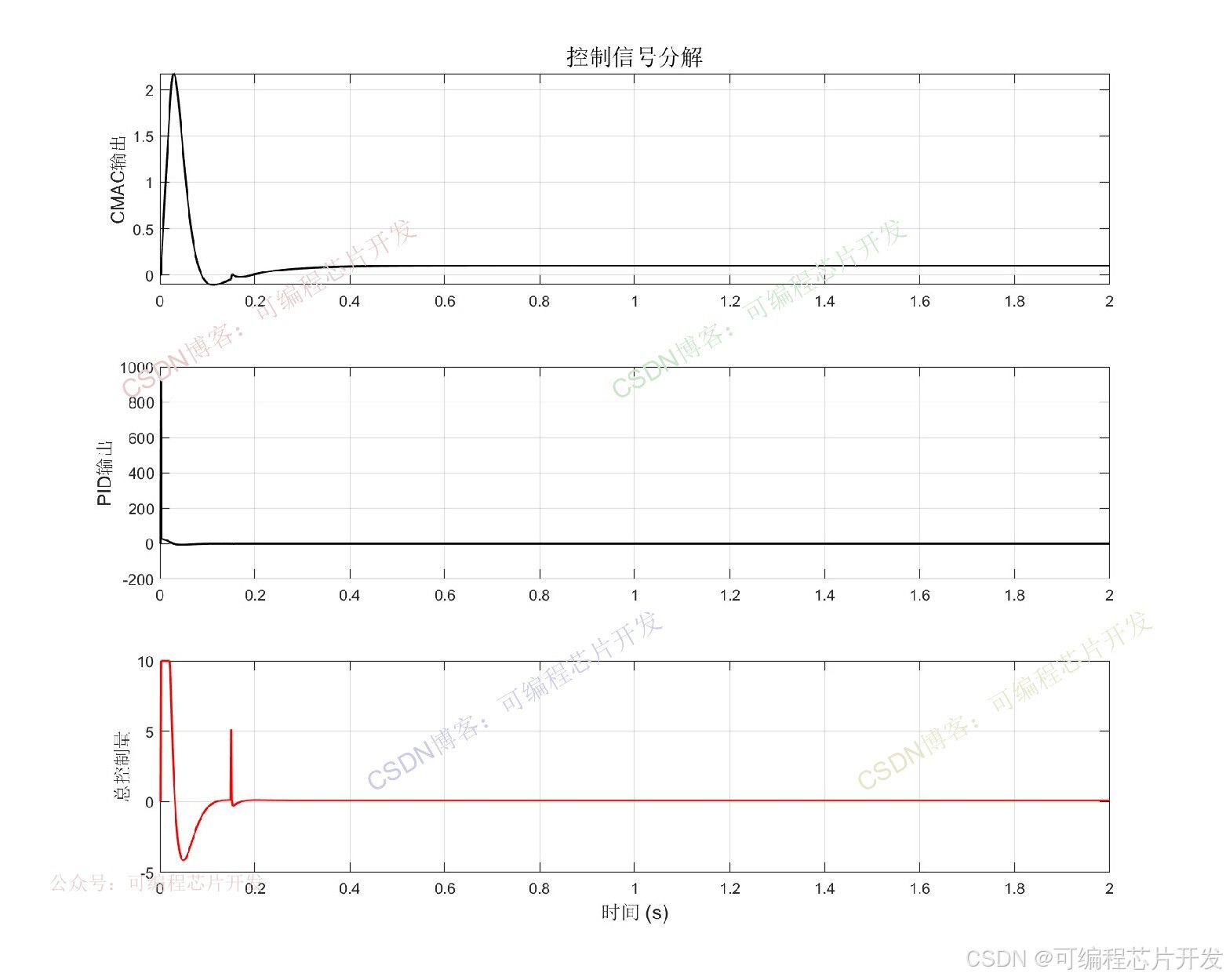
% 图2: 控制信号
figure('Name', '控制信号', 'Position', [100, 200, 1000, 800]);
subplot(3,1,1);
plot(sim_data.time, sim_data.un, 'k-', 'LineWidth', 1.2);
grid on;
ylabel('CMAC输出', 'FontSize', 11);
title('控制信号分解', 'FontSize', 14);
subplot(3,1,2);
plot(sim_data.time, sim_data.up, 'k-', 'LineWidth', 1.2);
grid on;
ylabel('PID输出', 'FontSize', 11);
subplot(3,1,3);
plot(sim_data.time, sim_data.u, 'r-', 'LineWidth', 1.2);
grid on;
xlabel('时间 (s)', 'FontSize', 12);
ylabel('总控制量', 'FontSize', 11);
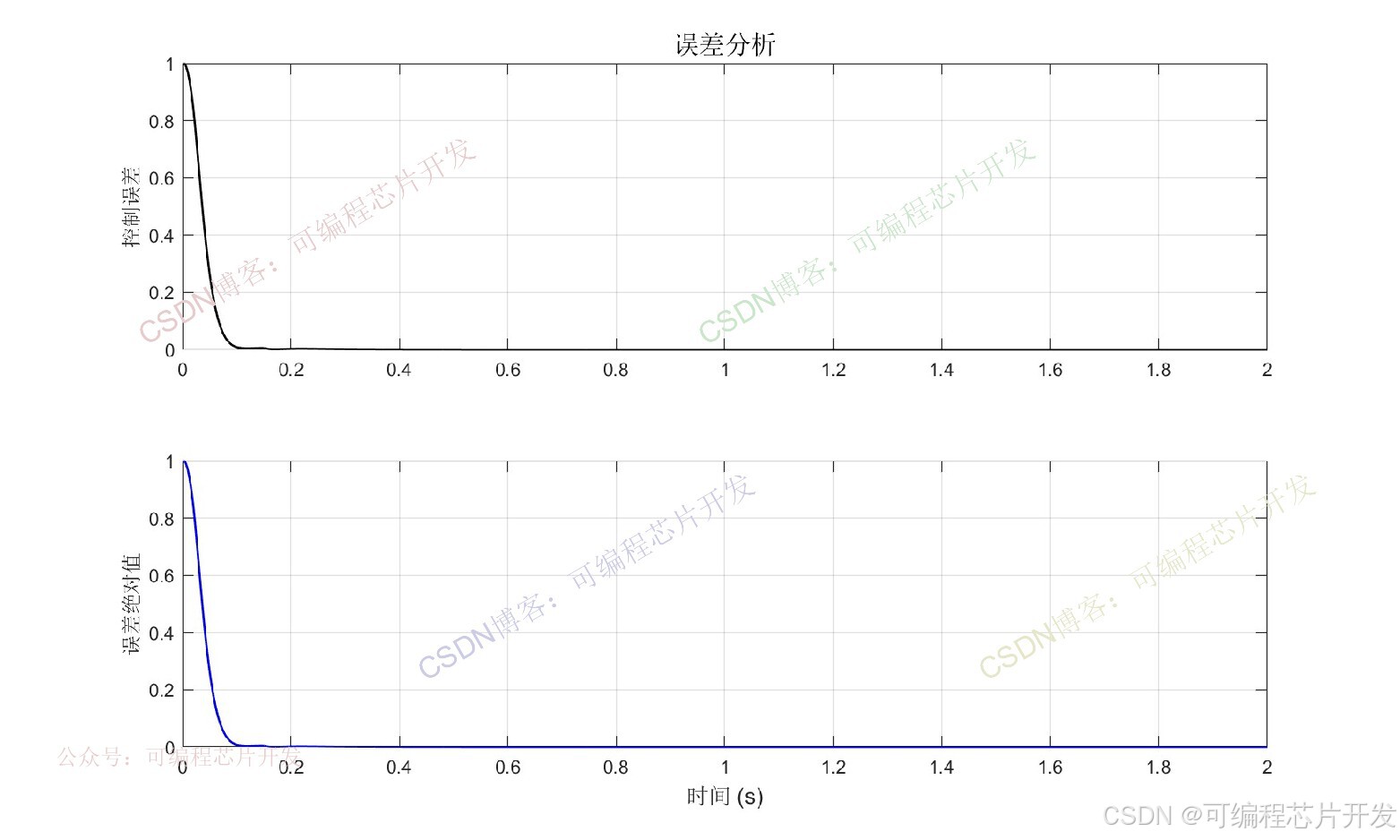
% 图3: 误差分析
figure('Name', '误差分析', 'Position', [100, 300, 1000, 600]);
subplot(2,1,1);
plot(sim_data.time, sim_data.error, 'k-', 'LineWidth', 1.2);
grid on;
ylabel('控制误差', 'FontSize', 11);
title('误差分析', 'FontSize', 14);
subplot(2,1,2);
plot(sim_data.time, abs(sim_data.error), 'b-', 'LineWidth', 1.2);
grid on;
xlabel('时间 (s)', 'FontSize', 12);
ylabel('误差绝对值', 'FontSize', 11);
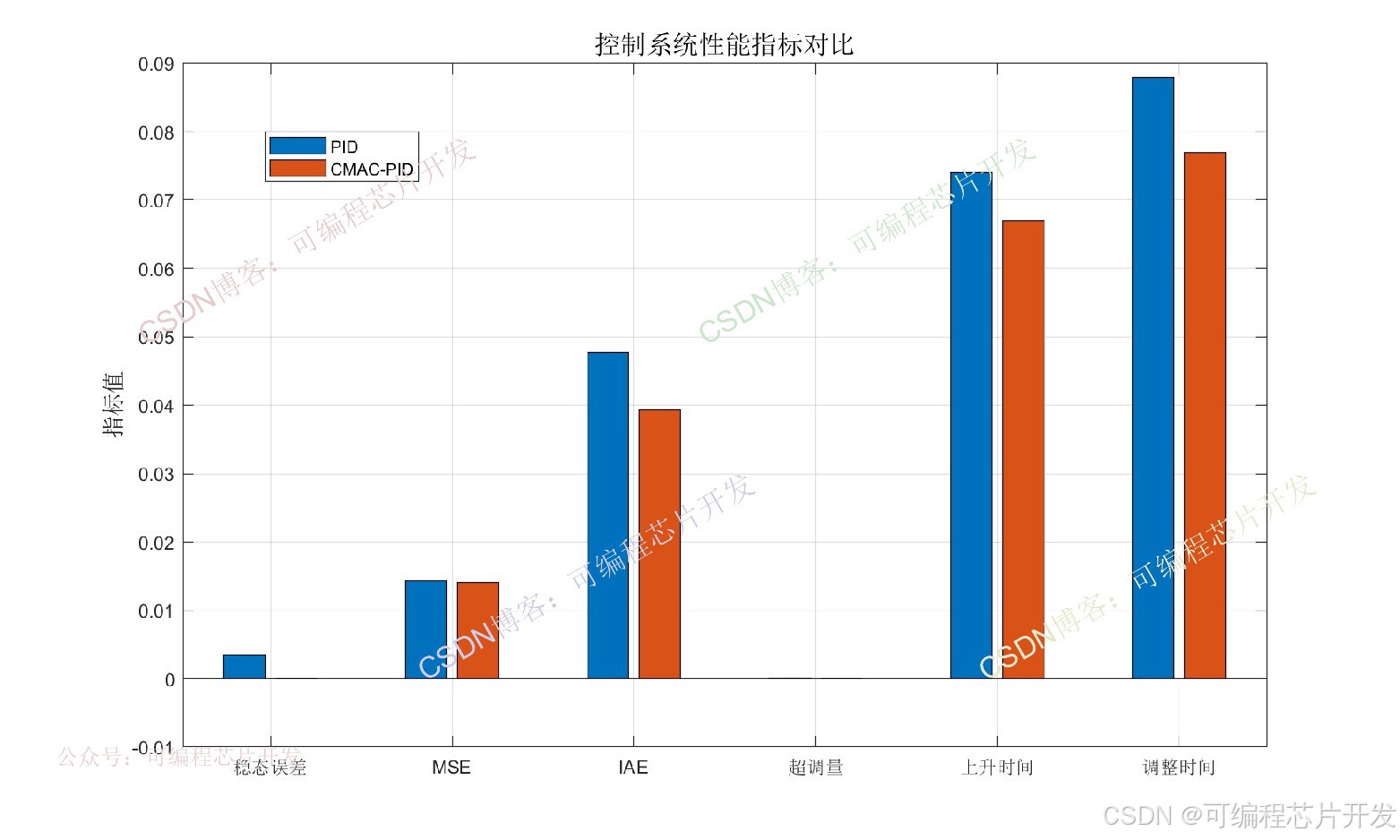
% 图4: 性能指标条形图
figure('Name', '性能指标', 'Position', [100, 400, 1000, 600]);
metrics1 = [performance.steady_state_error, performance.mse, ...
performance.iae, performance.overshoot/100, ...
performance.rise_time, performance.settling_time];
load R0.mat
metrics2 = metrics;
bar([metrics2;metrics1]');
grid on;
ylabel('指标值', 'FontSize', 12);
title('控制系统性能指标对比', 'FontSize', 14);
set(gca, 'XTickLabel', {'稳态误差', 'MSE', 'IAE', '超调量', '上升时间', '调整时间'});
legend('PID','CMAC-PID');
1304.系统原理简介
CMAC 是一种查表式局部逼近网络,其结构模仿小脑"并行分布处理"机制,核心优势体现在两点:
局部泛化能力:CMAC仅激活与输入相关的少量神经元(存储单元),而非全网络激活,学习过程仅更新局部权重,大幅提升学习速度,满足实时控制需求;
容错性强:单个存储单元故障仅影响局部输入区域,不会导致整个控制系统失效,适合工业恶劣环境;
无需精确数学模型:通过样本学习即可逼近系统未知动态,无需提前建立被控对象的非线性数学模型,降低工程应用门槛。
具体的实现步骤如下:
步骤1:采集系统反馈与计算偏差

步骤2:PID控制器输出计算
根据选择的PID类型(增量式 / 位置式)计算u_PID(k):

步骤3:CMAC控制器输出计算

步骤4:复合控制器总输出
将PID输出与CMAC补偿输出叠加,得到总控制量u (k),作用于被控对象(如电机驱动器、阀门控制器):
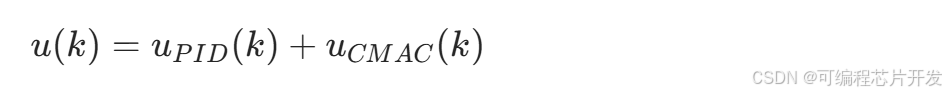
步骤5:CMAC权重在线更新
为适应系统参数时变与外部扰动,需实时更新CMAC权重:

步骤6:迭代循环
等待下一个采样周期T,返回步骤1,重复"采集-计算-输出-更新"流程,直到系统停止运行或设定值变更。
5.参考文献
1\]侯世英,时文飞,万江.基于CMAC-PID控制的柴油发电机组的建模与仿真\[J\].系统仿真学报, 2007, 19(13):5.DOI:10.3969/j.issn.1004-731X.2007.13.042. \[2\]张伟,朱大奇,孔敏,等.基于改进的CMAC神经网络与PID并行控制的研究\[J\].计算机测量与控制, 2005, 13(12):3.DOI:10.3321/j.issn:1671-4598.2005.12.021. ## 6.完整工程文件 **v** **v** **关注后,回复关键词:****a1**