Week 18: 深度学习补遗：Stacking和量子运算Deutsch算法

摘要

本周在完成了李宏毅老师的ML Lecture 2017后，切换到了ML Lecture 2021进行学习，着重学习注意力机制等知识。同时继续推进量子计算相关学习内容。

Abstract

After completing Professor Hung-yi Lee's ML Lecture 2017 this week, I switched to study ML Lecture 2021, focusing on topics like attention mechanisms. Concurrently, I continued advancing my learning in quantum computing-related content.

1. Stacking

Stacking的类似于对于nnn个分类系统f1...fnf_1\dots f_nf1...fn，输入xxx输入这nnn个分类系统中得到了nnn个输出γ1...γn\gamma_1\dots\gamma_nγ1...γn，最后输入一个训练的分类器中导出结果。

最后的这个Final Classifier不需要太复杂，使用简单的Logistics回归即可。需要注意的是，需要将训练前面nnn个分类系统的数据集与训练Final Classifier的数据集分开，保证Final Classifier的权重准确性。

2. Self-Attention 自注意力

在传统、普通的机器学习应用中，输入一般是个定长的向量，但很多情况下（例如图、语音、文字等输入中），输入常常是一组不定长向量。通常的任务类型分为Sequence to Sequence、Sequence Labeling、Encoder-Only、Decoder-Only等等。

对于Sequence Labeling，即输入nnn个向量，一一对应的基于nnn个向量的输出。直观的想法是将每一个向量输入一个全连接层，对应一个输出。但对于例如一个英文句子"I saw a saw"而言，两个"saw"的语义和词性截然不同，但是对于一个全连接网络而言，其应该会输出相同的结果，但假如我们给两个"saw"加上不同的Tag，普通的全连接网络并不能学习这种知识。

这时候，就需要给网络中加入上下文信息，对于全连接网络而言，当然可以把前后词汇直接连接到下一个词汇的网络中，前后文的长度叫做Window，即窗口大小。但对于一个非常长的序列而言，如果需要整个序列的信息，就需要将整个序列之间全部链接才能得到全部的前后文，如果采用全连接网络，参数量会非常恐怖。

对于自注意力而言，其会将输入的所有向量都生成对应的输出向量，其中含有整个句子前后文的信息。这样，将嵌入全局信息之后的向量再对下一层的全连接层直接进行输入，全连接层就可以考虑全局的信息，而非仅仅考虑单个单词的信息。

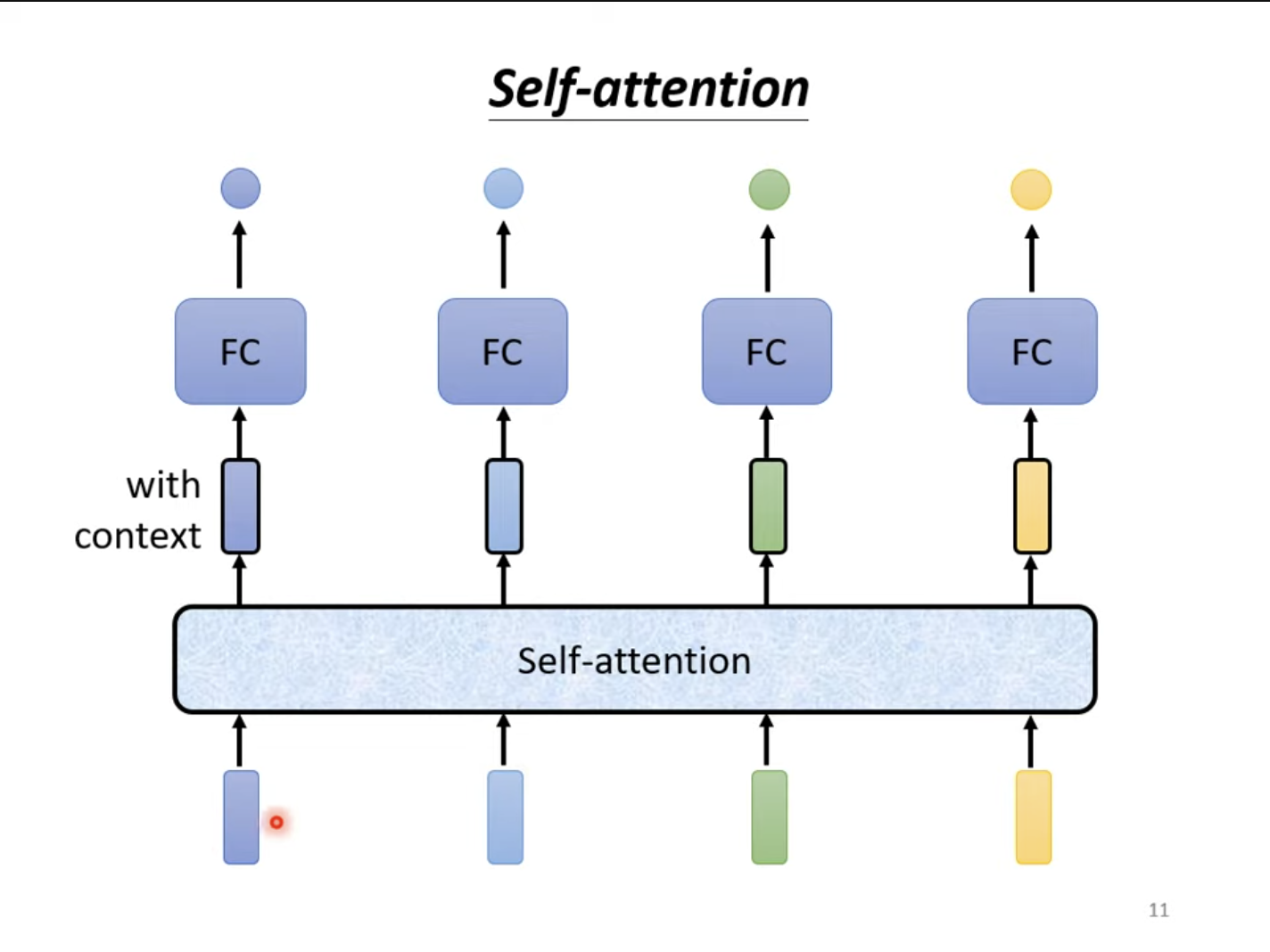
当然，自注意力层也可以进行嵌套，一层全连接层，一层自注意力层，使自注意力层专注于全局特征，全连接层专注于局部特征。

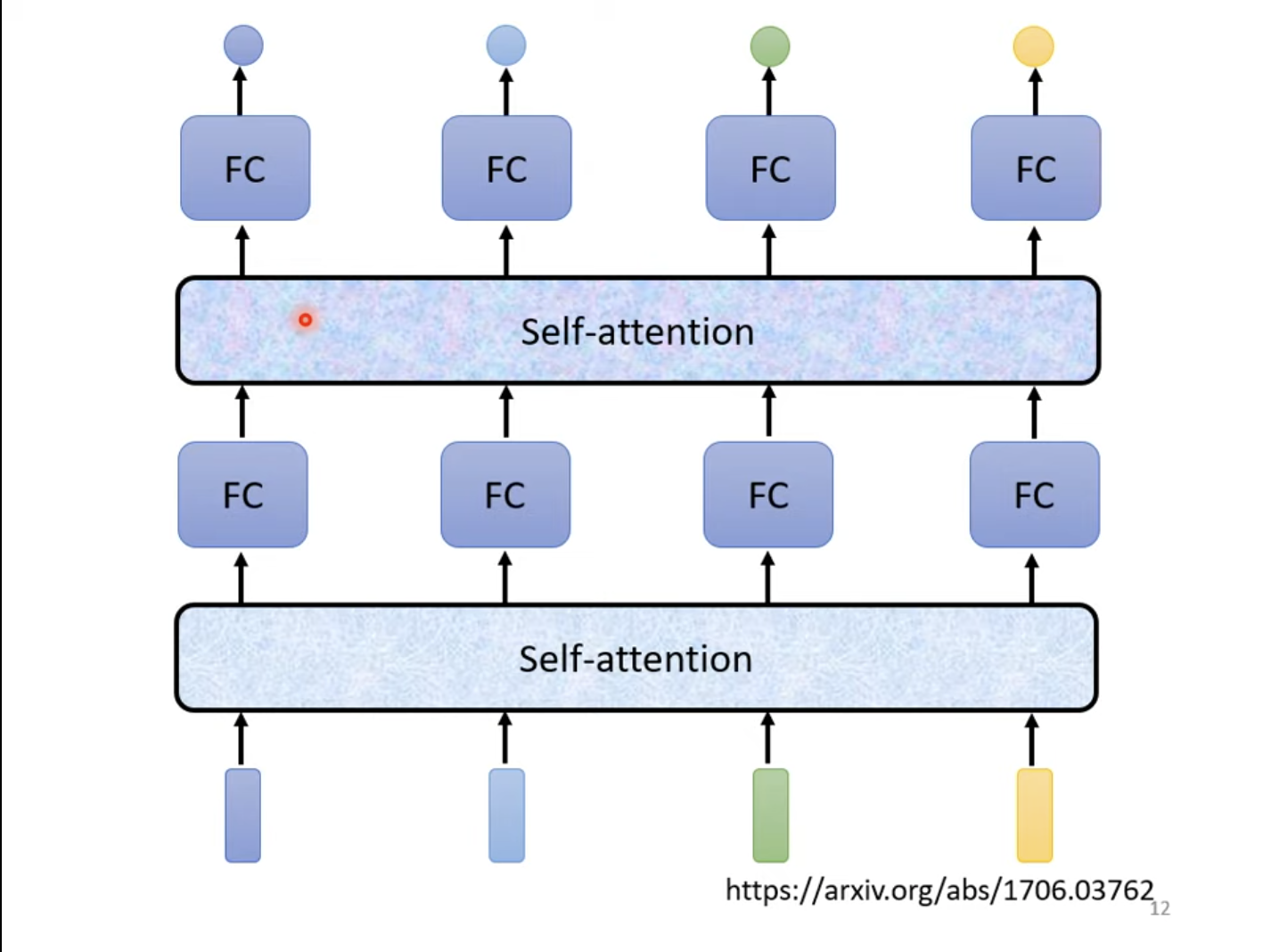
自注意力层的输入可以是整个模型的输入，也可以是其中的隐藏层的输入。已知自注意力层是考虑整个序列的输出结果，那么就需要求解两两输入之间的相关程度。求解两两之间的相关性有两种比较常用的方法，点积与加性方法。

点积就是将两个输入分别乘以矩阵WqW^qWq和WkW^kWk，得到两个结果qqq和kkk，对他们求点积q⋅kq\cdot kq⋅k，即逐元素的相乘相加，相关性就α=q⋅k\alpha=q\cdot kα=q⋅k。

加性的计算方法不同之处在于，经过变换求得qqq与kkk后，将其相加并经过一个激活函数（例如tanhtanhtanh）后再经过一次变换WWW后得到相关系数α\alphaα。

如今最常用的，也是被用在Transformer中的求解相关性的方法是点积方法。

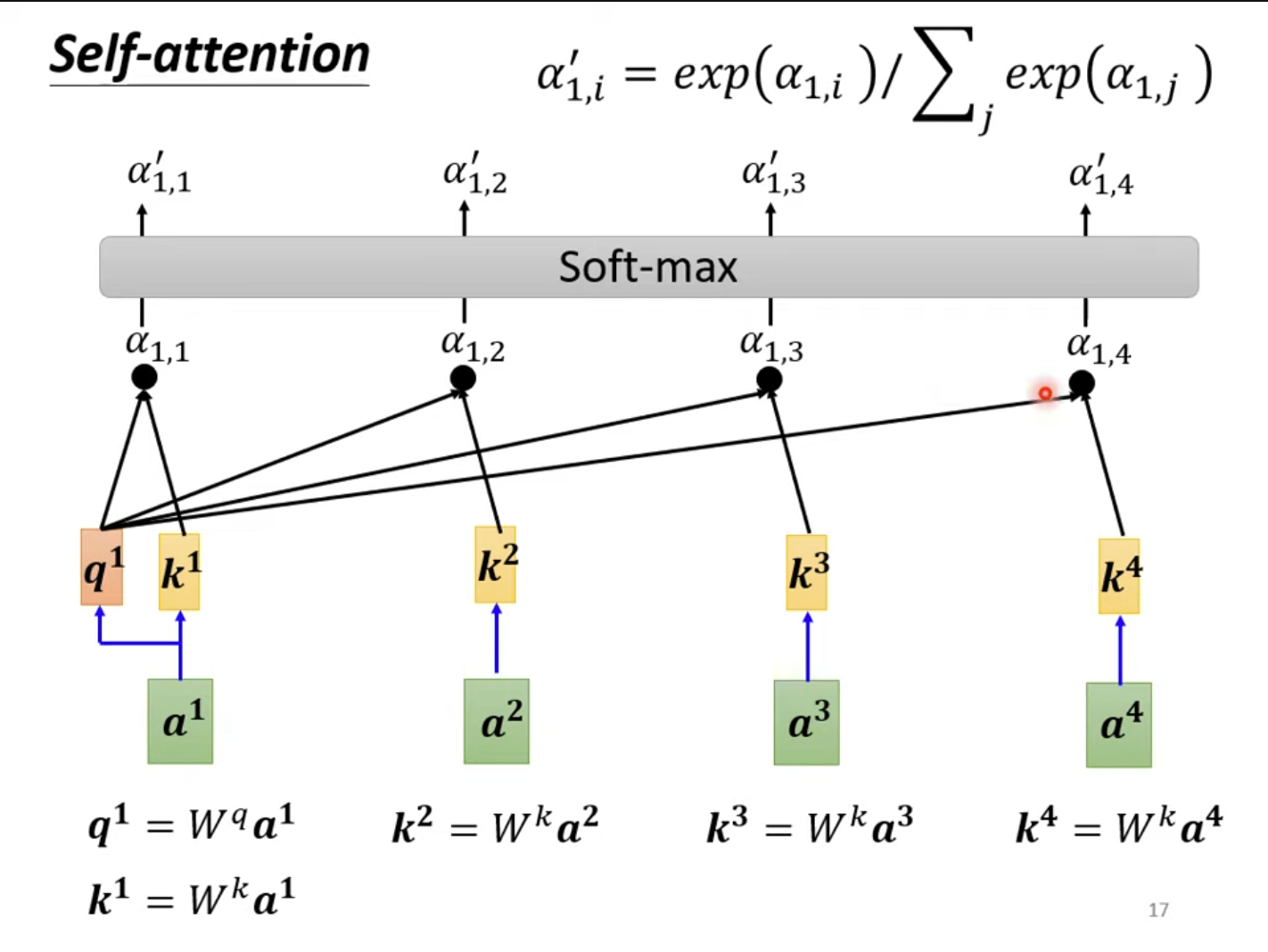
对于主元a1a^1a1，我们将其称为"Query"，要对每一个元素（包括其自身）ata^tat（称为"Key"）求解相关性。而每一个qtq^tqt、ktk^tkt都是由对应的元素乘以对应的变换得到。紧接着，对当前的qiq^iqi和每一个kjk^jkj求点积，得到一个注意力分数ai,ja_{i,j}ai,j。再把ai,j∣i=t\left.a_{i,j}\right|{i=t}ai,j∣i=t经过Softmax后得到一个激活的注意力分数ai,j′a'{i,j}ai,j′（可以换用别的激活函数）。
q1=Wqa1k1=Wka1k2=Wka2...a1,1=q1⋅k1a1,2=q1⋅k2... \begin{aligned} q^1 &= W^q a^1\\ k^1 &= W^k a^1\\ k^2 &= W^k a^2\\ &\dots \\ a_{1,1}&=q^1\cdot k^1\\ a_{1,2}&=q^1\cdot k^2\\ &\dots \\ \end{aligned} q1k1k2a1,1a1,2=Wqa1=Wka1=Wka2...=q1⋅k1=q1⋅k2...

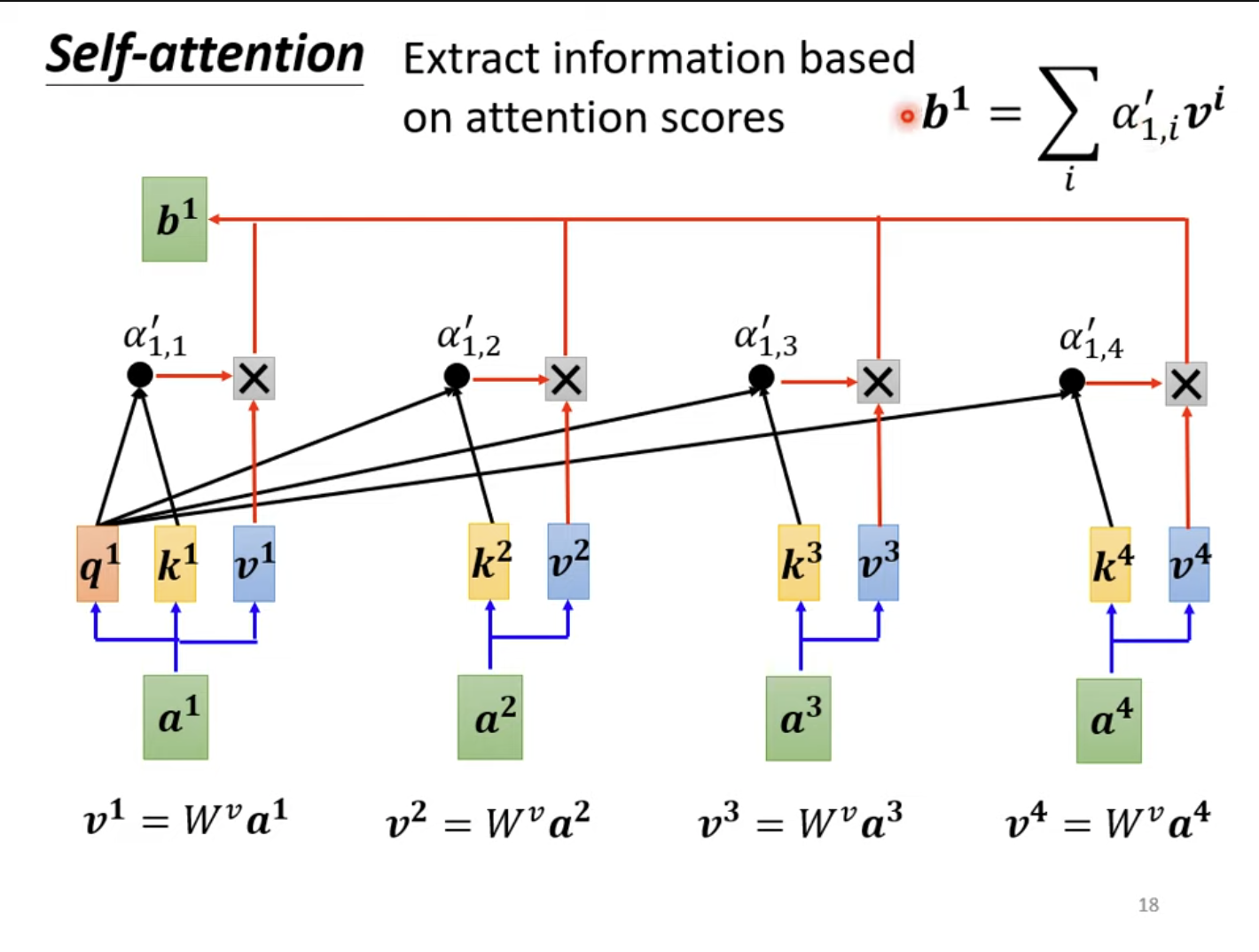
接着，将每个aia^iai乘以一个矩阵WvW^vWv得到对应的viv^ivi，即vi=Wvaiv^i=W^va^ivi=Wvai，再经过式子b1=∑ia1,i′vib^1=\sum_ia'_{1,i}v^ib1=∑ia1,i′vi即可得到a1a^1a1对应的输出。

对于每个aia^iai，求出其对应的bib^ibi，这样就完成了自注意力的求解。

3. 量子计算 Deutsch算法

Deutsch算法可以这么被描述。
(H⊗I) Uf (H⊗H) ∣0,1⟩ (H \otimes I) \, U_f \, (H \otimes H) \, \ket{0, 1} (H⊗I)Uf(H⊗H)∣0,1⟩

即将∣0,1⟩\ket{0,1}∣0,1⟩经过两个HadamardHadamardHadamard门后，进入UfU_fUf门，最后对两个输出一个输入HadamardHadamardHadamard门，一个输入单位门。

将∣0,1⟩\ket{0,1}∣0,1⟩，即∣0⟩⊗∣1⟩\ket{0}\otimes\ket{1}∣0⟩⊗∣1⟩输入HadamardHadamardHadamard门，H∣0⟩⊗H∣1⟩=12(∣0⟩+∣1⟩)⊗12(∣0⟩−∣1⟩)H\ket{0} \otimes H\ket{1} = \frac{1}{\sqrt{2}} (\ket{0} + \ket{1}) \otimes \frac{1}{\sqrt{2}} (\ket{0} - \ket{1})H∣0⟩⊗H∣1⟩=2 1(∣0⟩+∣1⟩)⊗2 1(∣0⟩−∣1⟩)。
UfU_fUf定义为∣x,y⟩↦∣x,y⊕f(x)⟩\ket{x, y} \mapsto \ket{x,y \oplus f(x)}∣x,y⟩↦∣x,y⊕f(x)⟩，那么对于∣12(∣0⟩+∣1⟩),12(∣0⟩−∣1⟩)⟩\ket{\frac{1}{\sqrt{2}} (\ket{0} + \ket{1}), \frac{1}{\sqrt{2}} (\ket{0} - \ket{1})}∣2 1(∣0⟩+∣1⟩),2 1(∣0⟩−∣1⟩)⟩的输入，xxx为控制比特，yyy为目标比特。即实际计算中，∣12(∣0⟩+∣1⟩),12(∣0⟩−∣1⟩)⟩=∣x,∣0⟩⊕f(x)−∣1⟩⊕f(x)2⟩\ket{\frac{1}{\sqrt{2}} (\ket{0} + \ket{1}), \frac{1}{\sqrt{2}} (\ket{0} - \ket{1})}=\ket{x,\frac{\ket{0}\oplus f(x)-\ket{1}\oplus f(x)}{\sqrt{2}}}∣2 1(∣0⟩+∣1⟩),2 1(∣0⟩−∣1⟩)⟩=∣x,2 ∣0⟩⊕f(x)−∣1⟩⊕f(x)⟩
又因为x=12(∣0⟩+∣1⟩)x=\frac{1}{\sqrt{2}} (\ket{0} + \ket{1})x=2 1(∣0⟩+∣1⟩)，由于量子计算的叠加性，实际上可以进行拆分，因此可以对∣0⟩\ket{0}∣0⟩和∣1⟩\ket{1}∣1⟩分开讨论。若f(x)=0f(x)=0f(x)=0，那么0⊕0=00\oplus0=00⊕0=0，1⊕0=11\oplus0=11⊕0=1，没有变化。若f(x)=1f(x)=1f(x)=1，那么0⊕1=10\oplus1=10⊕1=1，1⊕1=01\oplus1=01⊕1=0，完成翻转。也就是∣0⟩−∣1⟩2\frac{\ket{0}-\ket{1}}{\sqrt{2}}2 ∣0⟩−∣1⟩会被翻转为∣1⟩−∣0⟩2=−∣0⟩−∣1⟩2\frac{\ket{1}-\ket{0}}{\sqrt{2}}=-\frac{\ket{0}-\ket{1}}{\sqrt{2}}2 ∣1⟩−∣0⟩=−2 ∣0⟩−∣1⟩
因此，如果f(0)=f(1)f(0)=f(1)f(0)=f(1)，那么∣0⟩\ket{0}∣0⟩和∣1⟩\ket{1}∣1⟩同号，即在y=xy=xy=x上；如果f(0)≠f(1)f(0)\neq f(1)f(0)=f(1)，∣0⟩\ket{0}∣0⟩和∣1⟩\ket{1}∣1⟩异号，就在y=−xy=-xy=−x上。在经过一个HadamardHadamardHadamard门后，分别应该被反射到x=0x=0x=0和y=0y=0y=0上，即∣0⟩\ket{0}∣0⟩和∣1⟩\ket{1}∣1⟩。

因此，只需要经过一次测量，就可以测得是否f(1)=f(0)f(1)=f(0)f(1)=f(0)。

总结

本周学习了Stacking的集成学习方法，完成了ML Lecture 2017的学习。同时开始了ML Lecture 2021的学习，学习了自注意力相关底层知识，了解了自注意力层的整个运算步骤和原理，预计下周继续学习自注意力，对其底层逻辑继续进行深入研究。本周还进行了量子运算学习的推进，主要学习了Deutsch算法，了解了对死/活黑箱的探测原理，和其与传统运算的一些区别。