PyTorch nn.Linear 终极详解：从零理解线性层的一切（含可视化+完整代码）

努力还债的学术吗喽2025-10-01 9:33

🚀 PyTorch nn.Linear 终极详解：从零理解线性层的一切（含可视化+完整代码）

📚 阅读时长 ：约60分钟

🎯 难度等级 ：零基础到进阶

💡 前置知识 ：Python基础（不需要线性代数基础，我会讲解）

🔥 核心收获 ：彻底理解Linear层的本质、掌握各种使用场景、理解深度学习的基础 🎨 特色内容：包含完整PlantUML可视化

文章目录

  • [🚀 PyTorch nn.Linear 终极详解：从零理解线性层的一切（含可视化+完整代码）](#🚀 PyTorch nn.Linear 终极详解：从零理解线性层的一切（含可视化+完整代码）)
    • 🎯 前言：为什么Linear如此重要？ {#前言}
    • 🧠 从生物神经元到人工神经元 {#生物神经元}
      • [1. 生物神经元的启发](#1. 生物神经元的启发)
      • [2. 人工神经元模型](#2. 人工神经元模型)
      • [3. 可视化单个神经元（完整PlantUML代码）](#3. 可视化单个神经元（完整PlantUML代码）)
    • 在这里插入图片描述
    • 📐 Linear层的数学本质 {#数学本质}
      • [1. 单个样本的计算](#1. 单个样本的计算)
        • [🎯 具体例子：](#🎯 具体例子：)
        • [📊 分解计算过程：](#📊 分解计算过程：)
      • [2. 批量样本的计算](#2. 批量样本的计算)
      • [3. 多维张量的处理](#3. 多维张量的处理)
    • 🎨 图解神经元连接 {#图解神经元}
      • [1. Linear层全连接结构（3→2）](#1. Linear层全连接结构（3→2）)
      • [2. 权重矩阵W的结构](#2. 权重矩阵W的结构)
      • [3. 偏置向量b的结构](#3. 偏置向量b的结构)
      • [4. Linear层前向传播数据流](#4. Linear层前向传播数据流)
      • [5. 完整的数据流可视化代码](#5. 完整的数据流可视化代码)
    • 💻 手搓Linear层 {#手搓实现}
      • [1. 基础版本](#1. 基础版本)
      • [2. 高级版本（支持更多功能）](#2. 高级版本（支持更多功能）)
    • 🎯 PyTorch nn.Linear完全指南 {#pytorch实现}
      • [1. 基础用法](#1. 基础用法)
      • [2. 初始化策略](#2. 初始化策略)
      • [3. 组合使用示例](#3. 组合使用示例)
      • [4. 多层Linear网络结构可视化](#4. 多层Linear网络结构可视化)
    • 🚀 实战应用案例 {#实战应用}
      • [📊 应用1：维度变换和投影](#📊 应用1：维度变换和投影)
      • [🎨 应用2：分类任务](#🎨 应用2：分类任务)
      • [🔮 应用3：自编码器和生成模型](#🔮 应用3：自编码器和生成模型)
      • [🌟 应用4：Linear层在Transformer中的应用](#🌟 应用4：Linear层在Transformer中的应用)
    • 🛠️ 常见问题与技巧 {#常见问题}
      • [1. 性能优化](#1. 性能优化)
      • [2. 批量处理 vs 单样本处理](#2. 批量处理 vs 单样本处理)
      • [3. 梯度问题处理](#3. 梯度问题处理)
      • [4. 梯度流动示意图](#4. 梯度流动示意图)
      • [5. 调试技巧](#5. 调试技巧)
    • [🎨 Linear层参数初始化策略](#🎨 Linear层参数初始化策略)
    • 📚 总结与资源 {#总结}
      • [✨ 核心要点回顾](#✨ 核心要点回顾)
        • [1. 理论基础 ✅](#1. 理论基础 ✅)
        • [2. 实现细节 ✅](#2. 实现细节 ✅)
        • [3. 实战应用 ✅](#3. 实战应用 ✅)
        • [4. 优化技巧 ✅](#4. 优化技巧 ✅)
      • [🎯 关键公式速查](#🎯 关键公式速查)
      • [💡 最佳实践建议](#💡 最佳实践建议)
      • [📖 推荐学习资源](#📖 推荐学习资源)
        • [📚 深入学习](#📚 深入学习)
        • [🎥 视频课程](#🎥 视频课程)
        • [💻 实践项目](#💻 实践项目)
      • [🔬 扩展阅读](#🔬 扩展阅读)
    • [🙏 结语](#🙏 结语)
      • [🏷️ 标签](#🏷️ 标签)
      • [📝 作者寄语](#📝 作者寄语)

🎯 前言：为什么Linear如此重要？ {#前言}

大家好！今天我们要深入探讨深度学习中最基础、最重要的组件------线性层（Linear Layer） ！🎉

你可能会想："Linear层不就是个矩阵乘法吗，有什么好讲的？"

大错特错！ Linear层是：

  • 🧱 深度学习的基石：几乎所有神经网络都包含Linear层
  • 🔄 维度变换的魔法师：灵活改变数据的维度和表示
  • 🎯 特征提取的核心：学习数据中的线性关系
  • 💪 组合的力量：多个Linear层+激活函数=任意函数逼近器

如果你是小白，别担心！我会从最基础的概念讲起，保证你能理解每一个细节！😊

🧠 从生物神经元到人工神经元 {#生物神经元}

1. 生物神经元的启发

我们的大脑由约860亿个神经元组成。每个神经元的工作原理很简单：

  1. 接收信号：从其他神经元接收电信号
  2. 加权求和：不同输入有不同的重要性（权重）
  3. 激活输出：超过阈值就发送信号给下一个神经元

2. 人工神经元模型

python 复制代码 
# 一个简单的神经元示例
import numpy as np

class SimpleNeuron:
    """一个最简单的人工神经元"""
    
    def __init__(self, n_inputs):
        # 每个输入都有一个权重
        self.weights = np.random.randn(n_inputs)  # w1, w2, ..., wn
        # 一个偏置项（阈值）
        self.bias = np.random.randn()  # b
        
    def forward(self, inputs):
        """
        计算过程：
        output = w1*x1 + w2*x2 + ... + wn*xn + b
        """
        weighted_sum = np.dot(inputs, self.weights) + self.bias
        return weighted_sum

# 测试单个神经元
neuron = SimpleNeuron(3)  # 3个输入
x = np.array([1.0, 2.0, 3.0])  # 输入信号
output = neuron.forward(x)
print(f"输入: {x}")
print(f"权重: {neuron.weights}")
print(f"偏置: {neuron.bias}")
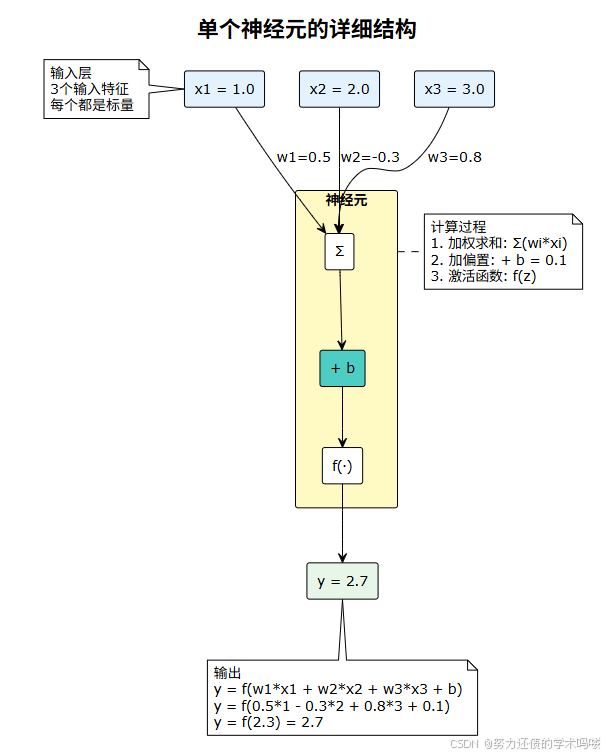
print(f"输出: {output}")

3. 可视化单个神经元（完整PlantUML代码）

这是单个神经元的详细结构图

📐 Linear层的数学本质 {#数学本质}

1. 单个样本的计算

当我们有一个样本时，Linear层做的就是：

y = x ⋅ W T + b \mathbf{y} = \mathbf{x} \cdot \mathbf{W}^T + \mathbf{b} y=x⋅WT+b

其中：

  • x \mathbf{x} x: 输入向量，形状 [in_features]
  • W \mathbf{W} W: 权重矩阵，形状 [out_features, in_features]
  • b \mathbf{b} b: 偏置向量，形状 [out_features]
  • y \mathbf{y} y: 输出向量，形状 [out_features]
🎯 具体例子：
python 复制代码 
import torch
import torch.nn as nn

# 创建一个Linear层：3个输入，2个输出
linear = nn.Linear(in_features=3, out_features=2)

# 单个样本输入
x = torch.tensor([1.0, 2.0, 3.0])  # shape: [3]

# 查看权重和偏置
print("权重矩阵 W:")
print(linear.weight)  # shape: [2, 3]
print("\n偏置向量 b:")
print(linear.bias)    # shape: [2]

# 前向传播
y = linear(x)  # shape: [2]
print(f"\n输入 x: {x}")
print(f"输出 y: {y}")

# 手动计算验证
y_manual = torch.matmul(x, linear.weight.T) + linear.bias
print(f"手动计算: {y_manual}")
print(f"结果一致: {torch.allclose(y, y_manual)}")
📊 分解计算过程：
python 复制代码 
# 让我们详细分解计算过程
def detailed_linear_computation(x, W, b):
    """
    详细展示Linear层的计算过程
    
    输入:
        x: [3] - 输入向量
        W: [2, 3] - 权重矩阵
        b: [2] - 偏置向量
    
    输出:
        y: [2] - 输出向量
    """
    print("="*50)
    print("🔍 Linear层计算详解")
    print("="*50)
    
    # 输入
    print(f"\n输入 x = {x.numpy()}")
    
    # 权重矩阵
    print(f"\n权重矩阵 W = ")
    print(W.numpy())
    
    # 偏置
    print(f"\n偏置 b = {b.numpy()}")
    
    # 计算第一个输出神经元
    y1 = W[0, 0] * x[0] + W[0, 1] * x[1] + W[0, 2] * x[2] + b[0]
    print(f"\ny[0] = W[0,0]*x[0] + W[0,1]*x[1] + W[0,2]*x[2] + b[0]")
    print(f"     = {W[0,0]:.2f}*{x[0]:.2f} + {W[0,1]:.2f}*{x[1]:.2f} + {W[0,2]:.2f}*{x[2]:.2f} + {b[0]:.2f}")
    print(f"     = {y1:.2f}")
    
    # 计算第二个输出神经元
    y2 = W[1, 0] * x[0] + W[1, 1] * x[1] + W[1, 2] * x[2] + b[1]
    print(f"\ny[1] = W[1,0]*x[0] + W[1,1]*x[1] + W[1,2]*x[2] + b[1]")
    print(f"     = {W[1,0]:.2f}*{x[0]:.2f} + {W[1,1]:.2f}*{x[1]:.2f} + {W[1,2]:.2f}*{x[2]:.2f} + {b[1]:.2f}")
    print(f"     = {y2:.2f}")
    
    # 最终输出
    y = torch.tensor([y1, y2])
    print(f"\n最终输出 y = {y.numpy()}")
    
    return y

# 测试
x = torch.tensor([1.0, 2.0, 3.0])
W = torch.tensor([[0.5, -0.3, 0.2],   # 第一个输出神经元的权重
                  [0.1, 0.4, -0.2]])   # 第二个输出神经元的权重
b = torch.tensor([0.1, -0.5])

y = detailed_linear_computation(x, W, b)

2. 批量样本的计算

当我们有多个样本（一个batch）时：

Y = X ⋅ W T + b \mathbf{Y} = \mathbf{X} \cdot \mathbf{W}^T + \mathbf{b} Y=X⋅WT+b

其中：

  • X \mathbf{X} X: 输入矩阵，形状 [batch_size, in_features]
  • W \mathbf{W} W: 权重矩阵，形状 [out_features, in_features]
  • b \mathbf{b} b: 偏置向量，形状 [out_features]（广播到每个样本）
  • Y \mathbf{Y} Y: 输出矩阵，形状 [batch_size, out_features]
python 复制代码 
# 批量样本示例
batch_size = 4
in_features = 3
out_features = 2

# 创建Linear层
linear = nn.Linear(in_features, out_features)

# 批量输入
X = torch.randn(batch_size, in_features)  # shape: [4, 3]
print(f"输入 X shape: {X.shape}")
print(f"输入 X:\n{X}")

# 前向传播
Y = linear(X)  # shape: [4, 2]
print(f"\n输出 Y shape: {Y.shape}")
print(f"输出 Y:\n{Y}")

# 验证每个样本的计算
print("\n逐样本验证:")
for i in range(batch_size):
    y_i = linear(X[i])
    print(f"样本{i}: 输入{X[i].shape} -> 输出{y_i.shape}")
    print(f"  与批量计算结果一致: {torch.allclose(Y[i], y_i)}")

3. 多维张量的处理

Linear层可以处理任意维度的输入，只要最后一维匹配即可：

python 复制代码 
def test_multidimensional_linear():
    """测试Linear层处理多维输入"""
    
    linear = nn.Linear(10, 5)
    
    # 2D输入：[batch_size, in_features]
    x_2d = torch.randn(32, 10)
    y_2d = linear(x_2d)
    print(f"2D: {x_2d.shape} -> {y_2d.shape}")
    
    # 3D输入：[batch_size, seq_len, in_features]
    x_3d = torch.randn(32, 100, 10)
    y_3d = linear(x_3d)
    print(f"3D: {x_3d.shape} -> {y_3d.shape}")
    
    # 4D输入：[batch_size, height, width, in_features]
    x_4d = torch.randn(32, 28, 28, 10)
    y_4d = linear(x_4d)
    print(f"4D: {x_4d.shape} -> {y_4d.shape}")
    
    # 5D输入：[batch_size, time, height, width, in_features]
    x_5d = torch.randn(32, 10, 28, 28, 10)
    y_5d = linear(x_5d)
    print(f"5D: {x_5d.shape} -> {y_5d.shape}")
    
    return y_2d, y_3d, y_4d, y_5d

# 运行测试
print("🔬 测试多维输入:")
test_multidimensional_linear()

🎨 图解神经元连接 {#图解神经元}

1. Linear层全连接结构（3→2）

以下是一个3输入2输出的Linear层完整连接结构

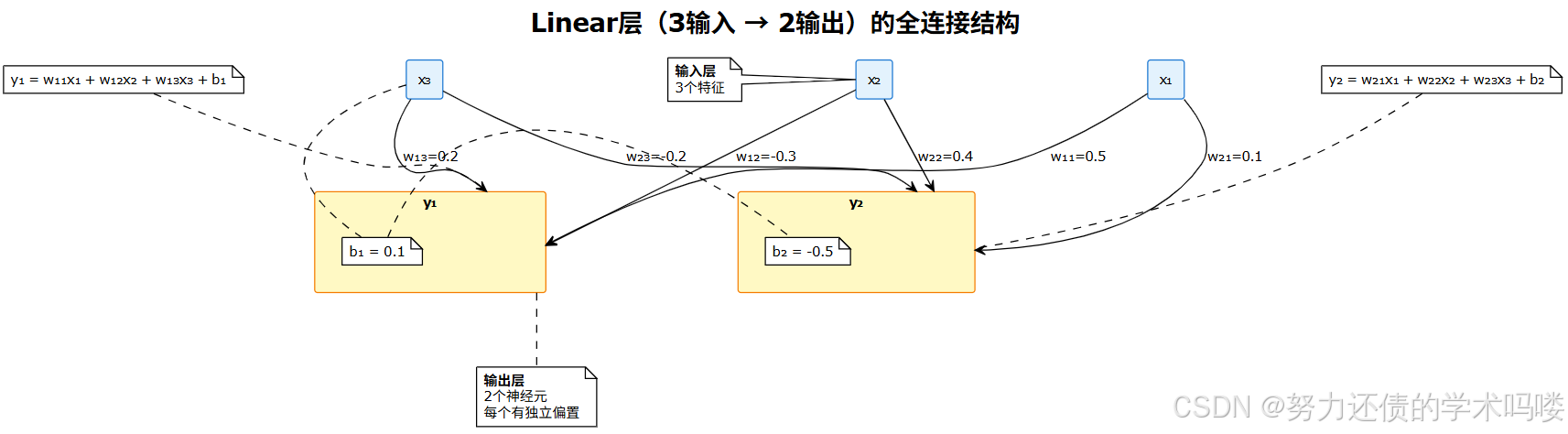
2. 权重矩阵W的结构

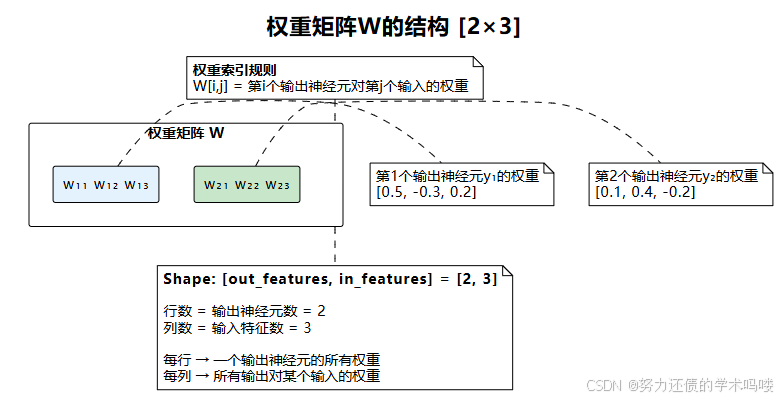
3. 偏置向量b的结构

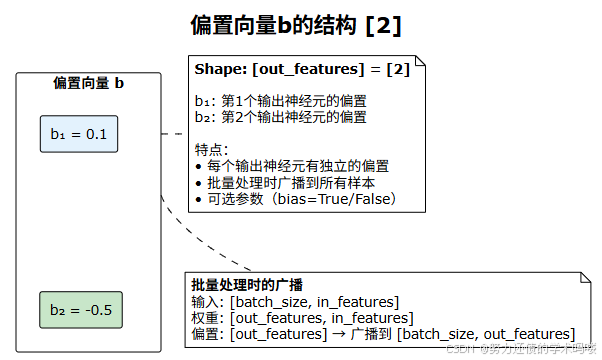
4. Linear层前向传播数据流

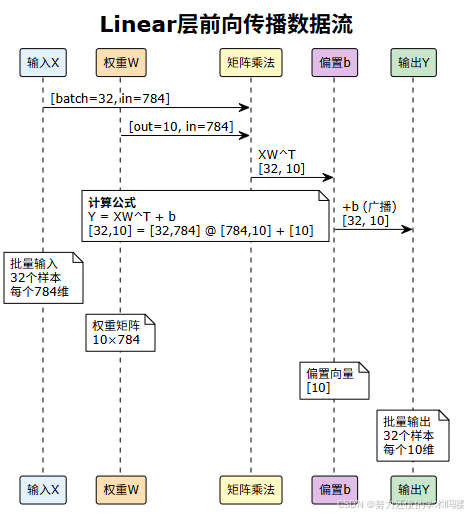
5. 完整的数据流可视化代码

python 复制代码 
def visualize_data_flow():
    """可视化Linear层的完整数据流"""
    
    print("="*60)
    print("📊 Linear层数据流可视化")
    print("="*60)
    
    # 设置参数
    batch_size = 2
    in_features = 3
    out_features = 2
    
    # 创建示例数据
    X = torch.tensor([
        [1.0, 2.0, 3.0],  # 样本1
        [4.0, 5.0, 6.0]   # 样本2
    ])
    
    W = torch.tensor([
        [0.1, 0.2, 0.3],  # y1的权重
        [0.4, 0.5, 0.6]   # y2的权重
    ])
    
    b = torch.tensor([0.1, -0.1])  # 偏置
    
    print(f"\n输入 X: shape={X.shape}")
    print(X)
    
    print(f"\n权重 W: shape={W.shape}")
    print(W)
    
    print(f"\n偏置 b: shape={b.shape}")
    print(b)
    
    # 详细计算过程
    print("\n" + "="*40)
    print("计算过程:")
    print("="*40)
    
    # 矩阵乘法
    print("\n1️⃣ 矩阵乘法 X @ W.T:")
    XW = torch.matmul(X, W.T)
    print(f"   shape: {X.shape} @ {W.T.shape} = {XW.shape}")
    print(f"   结果:\n{XW}")
    
    # 加偏置
    print("\n2️⃣ 加偏置 (XW + b):")
    Y = XW + b
    print(f"   偏置广播: {b.shape} -> {XW.shape}")
    print(f"   结果:\n{Y}")
    
    # 逐元素验证
    print("\n" + "="*40)
    print("逐元素验证:")
    print("="*40)
    
    for i in range(batch_size):
        for j in range(out_features):
            # 计算 Y[i,j]
            value = 0
            calc_str = f"Y[{i},{j}] = "
            for k in range(in_features):
                value += X[i,k] * W[j,k]
                calc_str += f"{X[i,k]:.1f}*{W[j,k]:.1f}"
                if k < in_features - 1:
                    calc_str += " + "
            value += b[j]
            calc_str += f" + {b[j]:.1f} = {value:.1f}"
            print(calc_str)
            
            # 验证
            assert abs(Y[i,j] - value) < 1e-6, "计算错误!"
    
    print("\n✅ 所有计算验证通过!")
    
    return Y

# 运行可视化
result = visualize_data_flow()

💻 手搓Linear层 {#手搓实现}

让我们从零开始实现一个Linear层，完全理解其内部机制！

1. 基础版本

python 复制代码 
class MyLinear(nn.Module):
    """
    手搓实现Linear层 - 基础版本
    
    功能等价于 nn.Linear
    """
    
    def __init__(self, in_features: int, out_features: int, bias: bool = True):
        """
        参数:
            in_features: 输入特征数
            out_features: 输出特征数
            bias: 是否使用偏置
        """
        super(MyLinear, self).__init__()
        
        self.in_features = in_features
        self.out_features = out_features
        self.use_bias = bias
        
        # 创建权重参数 [out_features, in_features]
        self.weight = nn.Parameter(torch.empty(out_features, in_features))
        
        # 创建偏置参数 [out_features]
        if bias:
            self.bias = nn.Parameter(torch.empty(out_features))
        else:
            self.register_parameter('bias', None)
        
        # 初始化参数
        self.reset_parameters()
        
        print(f"✅ MyLinear初始化: {in_features} -> {out_features}")
        print(f"   权重shape: {self.weight.shape}")
        if self.use_bias:
            print(f"   偏置shape: {self.bias.shape}")
    
    def reset_parameters(self):
        """参数初始化（使用Xavier初始化）"""
        # Xavier均匀分布初始化
        nn.init.xavier_uniform_(self.weight)
        
        if self.use_bias:
            # 偏置初始化为0
            nn.init.zeros_(self.bias)
    
    def forward(self, x: torch.Tensor) -> torch.Tensor:
        """
        前向传播
        
        输入:
            x: [..., in_features] - 任意维度，最后一维必须是in_features
            
        输出:
            [..., out_features] - 保持输入的维度结构，最后一维变为out_features
        """
        # 线性变换: y = xW^T + b
        output = torch.matmul(x, self.weight.t())
        
        if self.use_bias:
            output = output + self.bias
        
        return output
    
    def extra_repr(self) -> str:
        """用于print时显示层信息"""
        return f'in_features={self.in_features}, out_features={self.out_features}, bias={self.use_bias}'


# 测试手搓的Linear层
def test_my_linear():
    """测试手搓的Linear层"""
    print("\n" + "="*50)
    print("🧪 测试手搓Linear层")
    print("="*50)
    
    # 创建两个层：PyTorch的和我们的
    in_features = 5
    out_features = 3
    
    torch_linear = nn.Linear(in_features, out_features)
    my_linear = MyLinear(in_features, out_features)
    
    # 复制权重，确保参数相同
    my_linear.weight.data = torch_linear.weight.data.clone()
    my_linear.bias.data = torch_linear.bias.data.clone()
    
    # 测试不同维度的输入
    test_inputs = [
        torch.randn(10, in_features),           # 2D
        torch.randn(4, 8, in_features),         # 3D
        torch.randn(2, 4, 8, in_features),      # 4D
    ]
    
    print("\n测试结果:")
    for i, x in enumerate(test_inputs):
        y_torch = torch_linear(x)
        y_mine = my_linear(x)
        
        print(f"\n输入{i+1} shape: {x.shape}")
        print(f"  PyTorch输出: {y_torch.shape}")
        print(f"  MyLinear输出: {y_mine.shape}")
        print(f"  结果一致: {torch.allclose(y_torch, y_mine, atol=1e-6)}")
    
    print("\n✅ 手搓Linear层测试通过!")

# 运行测试
test_my_linear()

2. 高级版本（支持更多功能）

python 复制代码 
class AdvancedLinear(nn.Module):
    """
    手搓实现Linear层 - 高级版本
    
    额外功能:
    - 支持多种初始化方式
    - 支持权重约束
    - 支持梯度裁剪
    - 统计功能
    """
    
    def __init__(
        self,
        in_features: int,
        out_features: int,
        bias: bool = True,
        init_method: str = 'xavier',
        weight_constraint: float = None,
        track_stats: bool = False
    ):
        super(AdvancedLinear, self).__init__()
        
        self.in_features = in_features
        self.out_features = out_features
        self.use_bias = bias
        self.init_method = init_method
        self.weight_constraint = weight_constraint
        self.track_stats = track_stats
        
        # 创建参数
        self.weight = nn.Parameter(torch.empty(out_features, in_features))
        if bias:
            self.bias = nn.Parameter(torch.empty(out_features))
        else:
            self.register_parameter('bias', None)
        
        # 统计信息
        if track_stats:
            self.register_buffer('num_batches', torch.tensor(0))
            self.register_buffer('running_mean', torch.zeros(out_features))
            self.register_buffer('running_var', torch.ones(out_features))
        
        # 初始化
        self.reset_parameters()
        
    def reset_parameters(self):
        """根据指定方法初始化参数"""
        if self.init_method == 'xavier':
            nn.init.xavier_uniform_(self.weight)
        elif self.init_method == 'kaiming':
            nn.init.kaiming_uniform_(self.weight, nonlinearity='relu')
        elif self.init_method == 'normal':
            nn.init.normal_(self.weight, mean=0, std=0.01)
        else:
            raise ValueError(f"Unknown init method: {self.init_method}")
        
        if self.use_bias:
            nn.init.zeros_(self.bias)
    
    def forward(self, x: torch.Tensor) -> torch.Tensor:
        """前向传播"""
        # 权重约束
        if self.weight_constraint is not None:
            with torch.no_grad():
                norm = self.weight.norm(2, dim=1, keepdim=True)
                desired = torch.clamp(norm, max=self.weight_constraint)
                self.weight.mul_(desired / (norm + 1e-7))
        
        # 线性变换
        output = F.linear(x, self.weight, self.bias)
        
        # 更新统计信息
        if self.track_stats and self.training:
            with torch.no_grad():
                # 计算批次统计
                batch_mean = output.mean(dim=0)
                batch_var = output.var(dim=0)
                
                # 更新running统计
                momentum = 0.1
                self.running_mean.mul_(1 - momentum).add_(batch_mean * momentum)
                self.running_var.mul_(1 - momentum).add_(batch_var * momentum)
                self.num_batches += 1
        
        return output
    
    def get_stats(self):
        """获取统计信息"""
        if not self.track_stats:
            return None
        
        return {
            'num_batches': self.num_batches.item(),
            'running_mean': self.running_mean,
            'running_var': self.running_var,
            'weight_mean': self.weight.mean().item(),
            'weight_std': self.weight.std().item(),
        }


# 测试高级Linear层
def test_advanced_linear():
    """测试高级Linear层的功能"""
    print("\n" + "="*50)
    print("🚀 测试高级Linear层")
    print("="*50)
    
    # 创建层
    layer = AdvancedLinear(
        in_features=10,
        out_features=5,
        init_method='kaiming',
        weight_constraint=2.0,
        track_stats=True
    )
    
    # 训练模式
    layer.train()
    
    # 多个批次的前向传播
    for i in range(3):
        x = torch.randn(32, 10)
        y = layer(x)
        print(f"\n批次 {i+1}:")
        print(f"  输入: {x.shape}")
        print(f"  输出: {y.shape}")
        print(f"  输出均值: {y.mean():.4f}")
        print(f"  输出标准差: {y.std():.4f}")
    
    # 查看统计信息
    stats = layer.get_stats()
    print("\n📊 统计信息:")
    print(f"  处理批次数: {stats['num_batches']}")
    print(f"  Running均值: {stats['running_mean']}")
    print(f"  Running方差: {stats['running_var']}")
    print(f"  权重均值: {stats['weight_mean']:.4f}")
    print(f"  权重标准差: {stats['weight_std']:.4f}")
    
    # 验证权重约束
    weight_norms = layer.weight.norm(2, dim=1)
    print(f"\n权重范数: {weight_norms}")
    print(f"最大范数: {weight_norms.max():.4f}")
    print(f"权重约束生效: {weight_norms.max() <= layer.weight_constraint + 1e-6}")

# 运行测试
test_advanced_linear()

🎯 PyTorch nn.Linear完全指南 {#pytorch实现}

1. 基础用法

python 复制代码 
import torch
import torch.nn as nn

def basic_linear_usage():
    """nn.Linear的基础用法"""
    print("="*50)
    print("📚 nn.Linear基础用法")
    print("="*50)
    
    # 1. 创建Linear层
    linear = nn.Linear(
        in_features=784,   # 输入特征数（例如：28x28的图像展平）
        out_features=10,   # 输出特征数（例如：10个分类）
        bias=True          # 是否使用偏置（默认True）
    )
    
    print(f"\n1️⃣ Linear层信息:")
    print(f"   {linear}")
    print(f"   权重shape: {linear.weight.shape}")
    print(f"   偏置shape: {linear.bias.shape}")
    print(f"   参数总数: {sum(p.numel() for p in linear.parameters())}")
    
    # 2. 不同维度的输入
    print("\n2️⃣ 处理不同维度输入:")
    
    # 2D输入（最常见）
    x_2d = torch.randn(32, 784)  # [batch_size, features]
    y_2d = linear(x_2d)
    print(f"   2D: {x_2d.shape} -> {y_2d.shape}")
    
    # 3D输入（序列数据）
    x_3d = torch.randn(16, 50, 784)  # [batch, seq_len, features]
    y_3d = linear(x_3d)
    print(f"   3D: {x_3d.shape} -> {y_3d.shape}")
    
    # 4D输入（图像特征图）
    x_4d = torch.randn(8, 4, 4, 784)  # [batch, h, w, features]
    y_4d = linear(x_4d)
    print(f"   4D: {x_4d.shape} -> {y_4d.shape}")
    
    # 3. 访问和修改参数
    print("\n3️⃣ 参数操作:")
    print(f"   权重均值: {linear.weight.mean():.4f}")
    print(f"   权重标准差: {linear.weight.std():.4f}")
    print(f"   偏置均值: {linear.bias.mean():.4f}")
    
    # 修改参数
    with torch.no_grad():
        linear.weight.fill_(0.01)  # 将权重设为0.01
        linear.bias.zero_()         # 将偏置设为0
    
    print(f"   修改后权重均值: {linear.weight.mean():.4f}")
    print(f"   修改后偏置均值: {linear.bias.mean():.4f}")
    
    # 4. 不带偏置的Linear层
    print("\n4️⃣ 不带偏置的Linear层:")
    linear_no_bias = nn.Linear(100, 50, bias=False)
    print(f"   {linear_no_bias}")
    print(f"   有偏置? {linear_no_bias.bias is not None}")
    
    return linear

# 运行基础示例
basic_linear_usage()

2. 初始化策略

python 复制代码 
def initialization_strategies():
    """不同的权重初始化策略"""
    print("\n" + "="*50)
    print("⚡ 权重初始化策略")
    print("="*50)
    
    def analyze_init(linear, name):
        """分析初始化后的权重分布"""
        w_mean = linear.weight.mean().item()
        w_std = linear.weight.std().item()
        w_min = linear.weight.min().item()
        w_max = linear.weight.max().item()
        
        print(f"\n{name}:")
        print(f"  均值: {w_mean:.4f}")
        print(f"  标准差: {w_std:.4f}")
        print(f"  最小值: {w_min:.4f}")
        print(f"  最大值: {w_max:.4f}")
        
        return w_mean, w_std
    
    in_features = 256
    out_features = 128
    
    # 1. 默认初始化（Xavier/Glorot均匀分布）
    linear1 = nn.Linear(in_features, out_features)
    analyze_init(linear1, "1️⃣ 默认初始化（Xavier均匀）")
    
    # 2. Xavier正态分布
    linear2 = nn.Linear(in_features, out_features)
    nn.init.xavier_normal_(linear2.weight)
    analyze_init(linear2, "2️⃣ Xavier正态分布")
    
    # 3. Kaiming初始化（He初始化，适合ReLU）
    linear3 = nn.Linear(in_features, out_features)
    nn.init.kaiming_normal_(linear3.weight, nonlinearity='relu')
    analyze_init(linear3, "3️⃣ Kaiming初始化（ReLU）")
    
    # 4. 正态分布初始化
    linear4 = nn.Linear(in_features, out_features)
    nn.init.normal_(linear4.weight, mean=0, std=0.02)
    analyze_init(linear4, "4️⃣ 正态分布（std=0.02）")
    
    # 5. 均匀分布初始化
    linear5 = nn.Linear(in_features, out_features)
    nn.init.uniform_(linear5.weight, a=-0.1, b=0.1)
    analyze_init(linear5, "5️⃣ 均匀分布（-0.1, 0.1）")
    
    # 6. 常数初始化
    linear6 = nn.Linear(in_features, out_features)
    nn.init.constant_(linear6.weight, 0.01)
    analyze_init(linear6, "6️⃣ 常数初始化（0.01）")
    
    # 7. 正交初始化（保持梯度范数）
    linear7 = nn.Linear(in_features, out_features)
    nn.init.orthogonal_(linear7.weight)
    analyze_init(linear7, "7️⃣ 正交初始化")
    
    # 8. 稀疏初始化
    linear8 = nn.Linear(in_features, out_features)
    nn.init.sparse_(linear8.weight, sparsity=0.9)
    sparsity = (linear8.weight == 0).float().mean()
    print(f"\n8️⃣ 稀疏初始化:")
    print(f"  稀疏度: {sparsity:.2%}")
    
    # 初始化建议
    print("\n" + "="*40)
    print("💡 初始化建议:")
    print("="*40)
    print("• ReLU激活: 使用Kaiming初始化")
    print("• Tanh/Sigmoid激活: 使用Xavier初始化")
    print("• 深层网络: 考虑正交初始化")
    print("• 特殊需求: 自定义初始化")

# 运行初始化示例
initialization_strategies()

3. 组合使用示例

python 复制代码 
class LinearNetwork(nn.Module):
    """
    使用多个Linear层构建网络
    展示不同的组合方式
    """
    
    def __init__(self, input_dim, hidden_dims, output_dim):
        super(LinearNetwork, self).__init__()
        
        # 构建层列表
        layers = []
        prev_dim = input_dim
        
        # 隐藏层
        for i, hidden_dim in enumerate(hidden_dims):
            layers.append(nn.Linear(prev_dim, hidden_dim))
            layers.append(nn.ReLU())
            layers.append(nn.Dropout(0.2))
            prev_dim = hidden_dim
        
        # 输出层
        layers.append(nn.Linear(prev_dim, output_dim))
        
        # 组合成Sequential
        self.network = nn.Sequential(*layers)
        
        # 打印网络结构
        print(f"✅ 创建网络: {input_dim} -> {hidden_dims} -> {output_dim}")
        print(f"网络结构:\n{self.network}")
        
    def forward(self, x):
        return self.network(x)
    
    def count_parameters(self):
        """统计参数数量"""
        total = sum(p.numel() for p in self.parameters())
        trainable = sum(p.numel() for p in self.parameters() if p.requires_grad)
        
        print(f"\n📊 参数统计:")
        print(f"  总参数: {total:,}")
        print(f"  可训练参数: {trainable:,}")
        
        # 逐层统计
        print("\n逐层参数:")
        for i, module in enumerate(self.network):
            if isinstance(module, nn.Linear):
                params = sum(p.numel() for p in module.parameters())
                print(f"  Layer {i}: {params:,} 参数")
        
        return total


# 测试组合网络
def test_linear_network():
    """测试Linear层组合网络"""
    print("\n" + "="*50)
    print("🏗️ Linear层组合网络")
    print("="*50)
    
    # 创建网络
    net = LinearNetwork(
        input_dim=784,
        hidden_dims=[256, 128, 64],
        output_dim=10
    )
    
    # 统计参数
    net.count_parameters()
    
    # 测试前向传播
    x = torch.randn(32, 784)
    y = net(x)
    print(f"\n前向传播:")
    print(f"  输入: {x.shape}")
    print(f"  输出: {y.shape}")
    
    # 查看中间层输出
    print("\n中间层输出shape:")
    with torch.no_grad():
        intermediate = x
        for i, layer in enumerate(net.network):
            intermediate = layer(intermediate)
            if isinstance(layer, nn.Linear):
                print(f"  After layer {i}: {intermediate.shape}")
    
    return net

# 运行测试
network = test_linear_network()

4. 多层Linear网络结构可视化

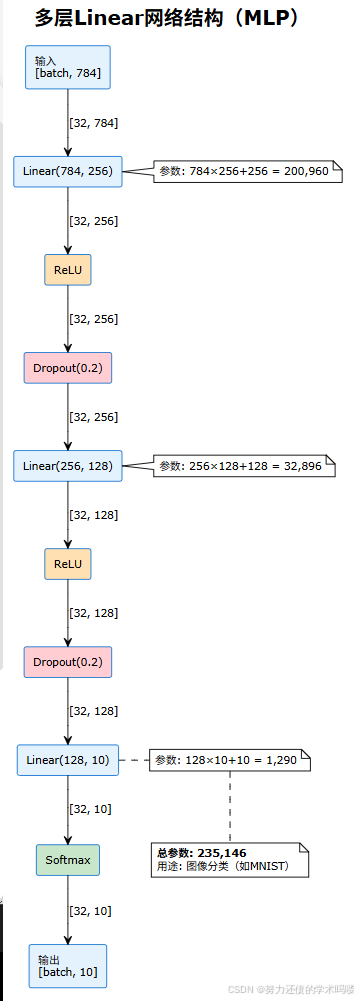
🚀 实战应用案例 {#实战应用}

📊 应用1：维度变换和投影

python 复制代码 
class DimensionTransformation:
    """
    使用Linear层进行维度变换和投影
    
    常见场景:
    - 特征降维（PCA的线性版本）
    - 特征升维（增加表达能力）
    - 投影到不同空间
    """
    
    def __init__(self):
        print("="*50)
        print("📊 维度变换和投影示例")
        print("="*50)
    
    def feature_reduction(self):
        """特征降维示例"""
        print("\n1️⃣ 特征降维（1024 -> 128）:")
        
        # 高维特征 -> 低维表示
        reducer = nn.Linear(1024, 128)
        
        # 输入：高维特征（比如图像特征）
        high_dim_features = torch.randn(32, 1024)
        
        # 降维
        low_dim_features = reducer(high_dim_features)
        
        print(f"  输入维度: {high_dim_features.shape}")
        print(f"  输出维度: {low_dim_features.shape}")
        print(f"  压缩率: {128/1024:.1%}")
        print(f"  参数量: {reducer.weight.numel() + reducer.bias.numel():,}")
        
        return low_dim_features
    
    def feature_expansion(self):
        """特征升维示例"""
        print("\n2️⃣ 特征升维（64 -> 512）:")
        
        # 低维特征 -> 高维表示
        expander = nn.Linear(64, 512)
        
        # 输入：低维特征
        low_dim_features = torch.randn(32, 64)
        
        # 升维
        high_dim_features = expander(low_dim_features)
        
        print(f"  输入维度: {low_dim_features.shape}")
        print(f"  输出维度: {high_dim_features.shape}")
        print(f"  扩展倍数: {512/64:.0f}x")
        
        return high_dim_features
    
    def multi_head_projection(self):
        """多头投影（类似多头注意力的投影）"""
        print("\n3️⃣ 多头投影（Transformer风格）:")
        
        d_model = 512
        n_heads = 8
        d_k = d_model // n_heads  # 64
        
        # Q, K, V投影
        q_proj = nn.Linear(d_model, d_model)
        k_proj = nn.Linear(d_model, d_model)
        v_proj = nn.Linear(d_model, d_model)
        
        # 输入特征
        x = torch.randn(32, 100, d_model)  # [batch, seq_len, d_model]
        
        # 投影
        Q = q_proj(x)  # [32, 100, 512]
        K = k_proj(x)  # [32, 100, 512]
        V = v_proj(x)  # [32, 100, 512]
        
        # 重塑为多头
        batch_size, seq_len = x.shape[:2]
        Q = Q.view(batch_size, seq_len, n_heads, d_k).transpose(1, 2)
        K = K.view(batch_size, seq_len, n_heads, d_k).transpose(1, 2)
        V = V.view(batch_size, seq_len, n_heads, d_k).transpose(1, 2)
        
        print(f"  输入: {x.shape}")
        print(f"  投影后: Q/K/V = {Q.shape}")
        print(f"  每个头的维度: {d_k}")
        
        return Q, K, V
    
    def cross_modal_projection(self):
        """跨模态投影（图像-文本）"""
        print("\n4️⃣ 跨模态投影（图像->文本空间）:")
        
        img_dim = 2048  # ResNet特征维度
        text_dim = 768  # BERT特征维度
        shared_dim = 512  # 共享空间维度
        
        # 图像投影器
        img_projector = nn.Linear(img_dim, shared_dim)
        # 文本投影器
        text_projector = nn.Linear(text_dim, shared_dim)
        
        # 模拟输入
        img_features = torch.randn(32, img_dim)
        text_features = torch.randn(32, text_dim)
        
        # 投影到共享空间
        img_shared = img_projector(img_features)
        text_shared = text_projector(text_features)
        
        # 计算相似度
        similarity = F.cosine_similarity(img_shared, text_shared)
        
        print(f"  图像特征: {img_features.shape} -> {img_shared.shape}")
        print(f"  文本特征: {text_features.shape} -> {text_shared.shape}")
        print(f"  相似度: {similarity.mean():.4f} ± {similarity.std():.4f}")
        
        return img_shared, text_shared
    
    def demo(self):
        """运行所有示例"""
        self.feature_reduction()
        self.feature_expansion()
        self.multi_head_projection()
        self.cross_modal_projection()

# 运行维度变换示例
dim_demo = DimensionTransformation()
dim_demo.demo()

🎨 应用2：分类任务

python 复制代码 
class ClassificationExample:
    """
    使用Linear层进行分类任务
    
    包括:
    - 二分类
    - 多分类
    - 多标签分类
    """
    
    def __init__(self):
        print("\n" + "="*50)
        print("🎯 分类任务示例")
        print("="*50)
    
    def binary_classification(self):
        """二分类示例"""
        print("\n1️⃣ 二分类（垃圾邮件检测）:")
        
        class BinaryClassifier(nn.Module):
            def __init__(self, input_dim):
                super().__init__()
                self.fc1 = nn.Linear(input_dim, 128)
                self.fc2 = nn.Linear(128, 64)
                self.fc3 = nn.Linear(64, 1)  # 输出1个值
                self.dropout = nn.Dropout(0.2)
                
            def forward(self, x):
                x = F.relu(self.fc1(x))
                x = self.dropout(x)
                x = F.relu(self.fc2(x))
                x = self.dropout(x)
                x = self.fc3(x)
                return torch.sigmoid(x)  # Sigmoid激活
        
        # 创建模型
        model = BinaryClassifier(input_dim=100)
        
        # 模拟输入（词向量特征）
        x = torch.randn(32, 100)
        
        # 预测
        predictions = model(x)
        
        print(f"  输入: {x.shape}")
        print(f"  输出: {predictions.shape}")
        print(f"  预测概率范围: [{predictions.min():.3f}, {predictions.max():.3f}]")
        
        # 转换为类别
        classes = (predictions > 0.5).float()
        print(f"  正样本比例: {classes.mean():.2%}")
        
        return model
    
    def multiclass_classification(self):
        """多分类示例"""
        print("\n2️⃣ 多分类（MNIST数字识别）:")
        
        class MultiClassifier(nn.Module):
            def __init__(self, input_dim, num_classes):
                super().__init__()
                self.fc1 = nn.Linear(input_dim, 256)
                self.fc2 = nn.Linear(256, 128)
                self.fc3 = nn.Linear(128, num_classes)
                self.dropout = nn.Dropout(0.2)
                
            def forward(self, x):
                x = F.relu(self.fc1(x))
                x = self.dropout(x)
                x = F.relu(self.fc2(x))
                x = self.dropout(x)
                x = self.fc3(x)
                return F.log_softmax(x, dim=1)  # LogSoftmax
        
        # 创建模型
        model = MultiClassifier(input_dim=784, num_classes=10)
        
        # 模拟输入（28x28图像展平）
        x = torch.randn(32, 784)
        
        # 预测
        log_probs = model(x)
        probs = torch.exp(log_probs)
        
        print(f"  输入: {x.shape}")
        print(f"  输出: {log_probs.shape}")
        print(f"  概率和: {probs.sum(dim=1).mean():.4f}")  # 应该接近1
        
        # 获取预测类别
        predictions = torch.argmax(log_probs, dim=1)
        print(f"  预测类别: {predictions[:10].tolist()}")
        
        return model
    
    def multilabel_classification(self):
        """多标签分类示例"""
        print("\n3️⃣ 多标签分类（图像标签）:")
        
        class MultiLabelClassifier(nn.Module):
            def __init__(self, input_dim, num_labels):
                super().__init__()
                self.fc1 = nn.Linear(input_dim, 512)
                self.fc2 = nn.Linear(512, 256)
                self.fc3 = nn.Linear(256, num_labels)
                self.dropout = nn.Dropout(0.3)
                
            def forward(self, x):
                x = F.relu(self.fc1(x))
                x = self.dropout(x)
                x = F.relu(self.fc2(x))
                x = self.dropout(x)
                x = self.fc3(x)
                return torch.sigmoid(x)  # 每个标签独立的Sigmoid
        
        # 创建模型（20个可能的标签）
        model = MultiLabelClassifier(input_dim=2048, num_labels=20)
        
        # 模拟输入（图像特征）
        x = torch.randn(32, 2048)
        
        # 预测
        predictions = model(x)
        
        print(f"  输入: {x.shape}")
        print(f"  输出: {predictions.shape}")
        
        # 设置阈值获取标签
        threshold = 0.5
        labels = (predictions > threshold).float()
        avg_labels = labels.sum(dim=1).mean()
        
        print(f"  平均每个样本的标签数: {avg_labels:.2f}")
        
        # 显示一个样本的预测
        sample_pred = predictions[0]
        top_5_scores, top_5_indices = torch.topk(sample_pred, 5)
        print(f"  样本1的Top-5标签: {top_5_indices.tolist()}")
        print(f"  对应分数: {top_5_scores.tolist()}")
        
        return model
    
    def demo(self):
        """运行所有分类示例"""
        self.binary_classification()
        self.multiclass_classification()
        self.multilabel_classification()

# 运行分类示例
clf_demo = ClassificationExample()
clf_demo.demo()

🔮 应用3：自编码器和生成模型

python 复制代码 
class AutoencoderExample:
    """
    使用Linear层构建自编码器
    
    应用:
    - 数据压缩
    - 去噪
    - 特征学习
    """
    
    def __init__(self):
        print("\n" + "="*50)
        print("🔮 自编码器示例")
        print("="*50)
    
    def build_autoencoder(self):
        """构建基础自编码器"""
        
        class Autoencoder(nn.Module):
            def __init__(self, input_dim, encoding_dim):
                super().__init__()
                
                # 编码器
                self.encoder = nn.Sequential(
                    nn.Linear(input_dim, 256),
                    nn.ReLU(),
                    nn.Linear(256, 128),
                    nn.ReLU(),
                    nn.Linear(128, encoding_dim)  # 瓶颈层
                )
                
                # 解码器
                self.decoder = nn.Sequential(
                    nn.Linear(encoding_dim, 128),
                    nn.ReLU(),
                    nn.Linear(128, 256),
                    nn.ReLU(),
                    nn.Linear(256, input_dim),
                    nn.Sigmoid()  # 输出范围[0, 1]
                )
            
            def forward(self, x):
                encoded = self.encoder(x)
                decoded = self.decoder(encoded)
                return decoded, encoded
            
            def encode(self, x):
                return self.encoder(x)
            
            def decode(self, z):
                return self.decoder(z)
        
        print("\n1️⃣ 基础自编码器:")
        
        # 创建模型
        input_dim = 784  # 28x28图像
        encoding_dim = 32  # 压缩到32维
        
        model = Autoencoder(input_dim, encoding_dim)
        
        # 测试
        x = torch.randn(16, input_dim)
        reconstructed, encoded = model(x)
        
        print(f"  输入维度: {x.shape}")
        print(f"  编码维度: {encoded.shape}")
        print(f"  重构维度: {reconstructed.shape}")
        print(f"  压缩率: {encoding_dim/input_dim:.1%}")
        
        # 计算重构误差
        mse = F.mse_loss(reconstructed, x)
        print(f"  重构误差(MSE): {mse:.4f}")
        
        return model
    
    def build_vae(self):
        """构建变分自编码器（VAE）"""
        
        class VAE(nn.Module):
            def __init__(self, input_dim, latent_dim):
                super().__init__()
                
                # 编码器
                self.fc1 = nn.Linear(input_dim, 256)
                self.fc2 = nn.Linear(256, 128)
                self.fc_mu = nn.Linear(128, latent_dim)  # 均值
                self.fc_logvar = nn.Linear(128, latent_dim)  # 对数方差
                
                # 解码器
                self.fc3 = nn.Linear(latent_dim, 128)
                self.fc4 = nn.Linear(128, 256)
                self.fc5 = nn.Linear(256, input_dim)
            
            def encode(self, x):
                h = F.relu(self.fc1(x))
                h = F.relu(self.fc2(h))
                mu = self.fc_mu(h)
                logvar = self.fc_logvar(h)
                return mu, logvar
            
            def reparameterize(self, mu, logvar):
                """重参数化技巧"""
                std = torch.exp(0.5 * logvar)
                eps = torch.randn_like(std)
                return mu + eps * std
            
            def decode(self, z):
                h = F.relu(self.fc3(z))
                h = F.relu(self.fc4(h))
                return torch.sigmoid(self.fc5(h))
            
            def forward(self, x):
                mu, logvar = self.encode(x)
                z = self.reparameterize(mu, logvar)
                reconstructed = self.decode(z)
                return reconstructed, mu, logvar
        
        print("\n2️⃣ 变分自编码器（VAE）:")
        
        # 创建模型
        input_dim = 784
        latent_dim = 20
        
        model = VAE(input_dim, latent_dim)
        
        # 测试
        x = torch.randn(16, input_dim)
        reconstructed, mu, logvar = model(x)
        
        print(f"  输入维度: {x.shape}")
        print(f"  潜在空间维度: {latent_dim}")
        print(f"  均值shape: {mu.shape}")
        print(f"  对数方差shape: {logvar.shape}")
        
        # 生成新样本
        with torch.no_grad():
            z = torch.randn(5, latent_dim)
            generated = model.decode(z)
            print(f"\n  生成样本shape: {generated.shape}")
        
        return model
    
    def build_gan_discriminator(self):
        """构建GAN判别器"""
        
        class Discriminator(nn.Module):
            def __init__(self, input_dim):
                super().__init__()
                
                self.model = nn.Sequential(
                    nn.Linear(input_dim, 512),
                    nn.LeakyReLU(0.2),
                    nn.Dropout(0.3),
                    
                    nn.Linear(512, 256),
                    nn.LeakyReLU(0.2),
                    nn.Dropout(0.3),
                    
                    nn.Linear(256, 128),
                    nn.LeakyReLU(0.2),
                    nn.Dropout(0.3),
                    
                    nn.Linear(128, 1),
                    nn.Sigmoid()
                )
            
            def forward(self, x):
                return self.model(x)
        
        print("\n3️⃣ GAN判别器:")
        
        # 创建模型
        model = Discriminator(input_dim=784)
        
        # 测试
        real_data = torch.randn(16, 784)
        fake_data = torch.randn(16, 784)
        
        real_scores = model(real_data)
        fake_scores = model(fake_data)
        
        print(f"  输入维度: {real_data.shape}")
        print(f"  输出维度: {real_scores.shape}")
        print(f"  真实数据平均分数: {real_scores.mean():.4f}")
        print(f"  生成数据平均分数: {fake_scores.mean():.4f}")
        
        return model
    
    def demo(self):
        """运行所有自编码器示例"""
        self.build_autoencoder()
        self.build_vae()
        self.build_gan_discriminator()

# 运行自编码器示例
ae_demo = AutoencoderExample()
ae_demo.demo()

🌟 应用4：Linear层在Transformer中的应用

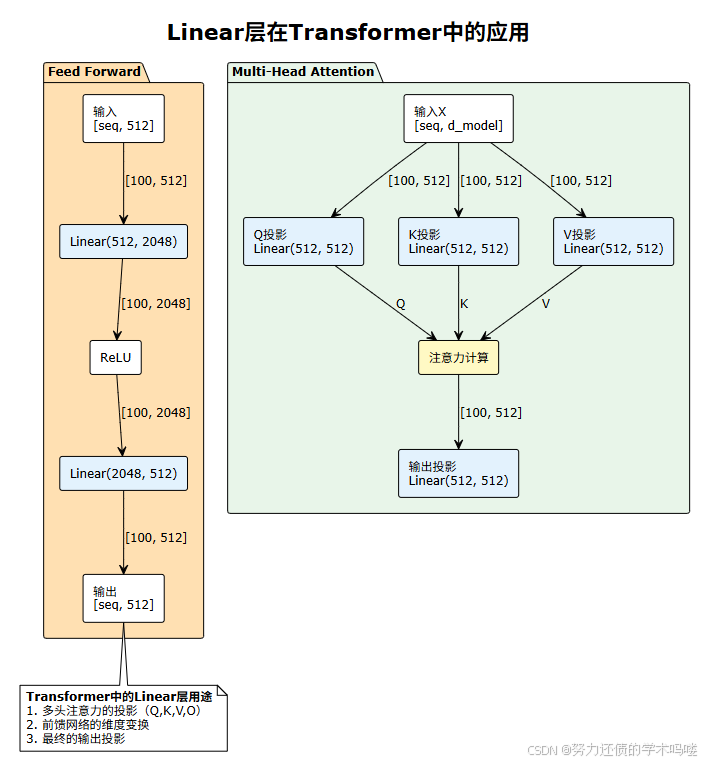
🛠️ 常见问题与技巧 {#常见问题}

1. 性能优化

python 复制代码 
def performance_optimization():
    """Linear层的性能优化技巧"""
    print("="*50)
    print("⚡ 性能优化技巧")
    print("="*50)
    
    # 1. 使用合适的数据类型
    print("\n1️⃣ 数据类型优化:")
    
    # Float32 vs Float16
    linear_fp32 = nn.Linear(1000, 1000)
    linear_fp16 = nn.Linear(1000, 1000).half()
    
    x = torch.randn(32, 1000)
    
    # 内存占用
    fp32_memory = linear_fp32.weight.element_size() * linear_fp32.weight.numel()
    fp16_memory = linear_fp16.weight.element_size() * linear_fp16.weight.numel()
    
    print(f"  FP32内存: {fp32_memory / 1024 / 1024:.2f} MB")
    print(f"  FP16内存: {fp16_memory / 1024 / 1024:.2f} MB")
    print(f"  节省: {(1 - fp16_memory/fp32_memory):.1%}")
    
    # 2. 批量处理
    print("\n2️⃣ 批量处理优化:")
    
    linear = nn.Linear(512, 256)
    
    # 单样本处理 vs 批量处理
    import time
    
    # 单样本
    single_samples = [torch.randn(512) for _ in range(100)]
    start = time.time()
    for sample in single_samples:
        _ = linear(sample)
    single_time = time.time() - start
    
    # 批量
    batch = torch.stack(single_samples)
    start = time.time()
    _ = linear(batch)
    batch_time = time.time() - start
    
    print(f"  单样本处理: {single_time*1000:.2f} ms")
    print(f"  批量处理: {batch_time*1000:.2f} ms")
    print(f"  加速: {single_time/batch_time:.1f}x")
    
    # 3. 权重共享
    print("\n3️⃣ 权重共享:")
    
    # 创建共享权重的层
    shared_linear = nn.Linear(100, 50)
    
    class SharedWeightNetwork(nn.Module):
        def __init__(self, shared_layer):
            super().__init__()
            self.shared = shared_layer
            self.fc1 = nn.Linear(200, 100)
            self.fc2 = nn.Linear(50, 10)
        
        def forward(self, x1, x2):
            # 两个分支共享同一个Linear层
            h1 = self.shared(self.fc1(x1))
            h2 = self.shared(self.fc1(x2))
            return self.fc2(h1), self.fc2(h2)
    
    model = SharedWeightNetwork(shared_linear)
    print(f"  共享层参数: {shared_linear.weight.shape}")
    print(f"  参数地址: {id(shared_linear.weight)}")

# 运行优化示例
performance_optimization()

2. 批量处理 vs 单样本处理

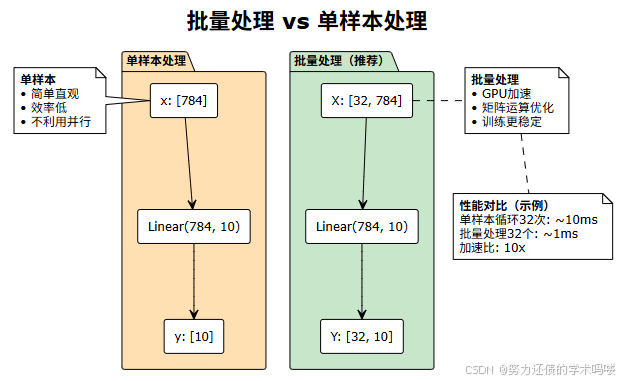
3. 梯度问题处理

python 复制代码 
def gradient_issues():
    """处理梯度相关问题"""
    print("\n" + "="*50)
    print("🔧 梯度问题处理")
    print("="*50)
    
    # 1. 梯度消失问题
    print("\n1️⃣ 梯度消失检测:")
    
    class DeepNetwork(nn.Module):
        def __init__(self, depth=10):
            super().__init__()
            layers = []
            for i in range(depth):
                layers.append(nn.Linear(100, 100))
                layers.append(nn.Sigmoid())  # Sigmoid容易导致梯度消失
            self.network = nn.Sequential(*layers)
        
        def forward(self, x):
            return self.network(x)
    
    # 创建深层网络
    model = DeepNetwork(depth=10)
    x = torch.randn(32, 100, requires_grad=True)
    y = model(x)
    loss = y.mean()
    loss.backward()
    
    # 检查梯度
    gradients = []
    for name, param in model.named_parameters():
        if param.grad is not None:
            gradients.append(param.grad.abs().mean().item())
    
    print(f"  第1层梯度: {gradients[0]:.6f}")
    print(f"  第5层梯度: {gradients[8]:.6f}")
    print(f"  第10层梯度: {gradients[18]:.6f}")
    
    # 2. 梯度爆炸问题
    print("\n2️⃣ 梯度裁剪:")
    
    class UnstableNetwork(nn.Module):
        def __init__(self):
            super().__init__()
            self.fc1 = nn.Linear(100, 100)
            self.fc2 = nn.Linear(100, 100)
            
            # 故意初始化大权重
            with torch.no_grad():
                self.fc1.weight.fill_(10)
                self.fc2.weight.fill_(10)
        
        def forward(self, x):
            x = self.fc1(x)
            x = self.fc2(x)
            return x
    
    model = UnstableNetwork()
    optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
    
    x = torch.randn(32, 100)
    y = model(x)
    loss = y.mean()
    
    # 计算梯度
    loss.backward()
    
    # 裁剪前的梯度范数
    total_norm_before = 0
    for p in model.parameters():
        if p.grad is not None:
            total_norm_before += p.grad.norm(2).item() ** 2
    total_norm_before = total_norm_before ** 0.5
    
    print(f"  裁剪前梯度范数: {total_norm_before:.2f}")
    
    # 梯度裁剪
    torch.nn.utils.clip_grad_norm_(model.parameters(), max_norm=1.0)
    
    # 裁剪后的梯度范数
    total_norm_after = 0
    for p in model.parameters():
        if p.grad is not None:
            total_norm_after += p.grad.norm(2).item() ** 2
    total_norm_after = total_norm_after ** 0.5
    
    print(f"  裁剪后梯度范数: {total_norm_after:.2f}")
    
    # 3. 梯度检查
    print("\n3️⃣ 梯度检查（调试用）:")
    
    def check_gradients(model):
        """检查模型的梯度健康度"""
        grad_stats = {}
        
        for name, param in model.named_parameters():
            if param.grad is not None:
                grad = param.grad
                grad_stats[name] = {
                    'mean': grad.mean().item(),
                    'std': grad.std().item(),
                    'min': grad.min().item(),
                    'max': grad.max().item(),
                    'has_nan': torch.isnan(grad).any().item(),
                    'has_inf': torch.isinf(grad).any().item()
                }
        
        return grad_stats
    
    # 创建简单模型
    simple_model = nn.Linear(10, 5)
    x = torch.randn(4, 10)
    y = simple_model(x)
    loss = y.sum()
    loss.backward()
    
    stats = check_gradients(simple_model)
    for name, stat in stats.items():
        print(f"\n  {name}:")
        print(f"    均值: {stat['mean']:.6f}")
        print(f"    标准差: {stat['std']:.6f}")
        print(f"    范围: [{stat['min']:.6f}, {stat['max']:.6f}]")
        print(f"    有NaN: {stat['has_nan']}")
        print(f"    有Inf: {stat['has_inf']}")

# 运行梯度问题示例
gradient_issues()

4. 梯度流动示意图

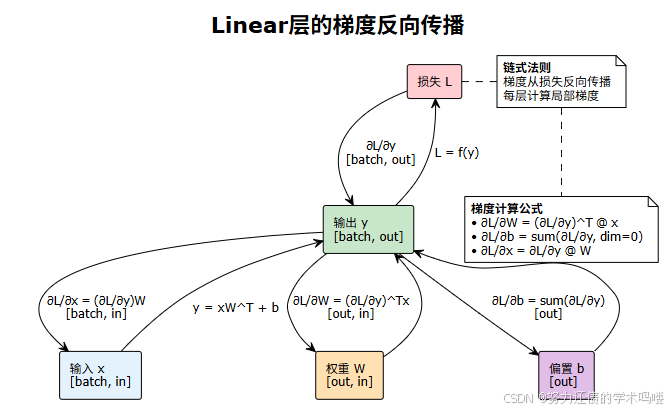
5. 调试技巧

python 复制代码 
def debugging_tips():
    """Linear层调试技巧"""
    print("\n" + "="*50)
    print("🐛 调试技巧")
    print("="*50)
    
    # 1. 打印中间输出
    print("\n1️⃣ Hook函数监控:")
    
    class DebugNetwork(nn.Module):
        def __init__(self):
            super().__init__()
            self.fc1 = nn.Linear(10, 20)
            self.fc2 = nn.Linear(20, 30)
            self.fc3 = nn.Linear(30, 5)
            
            # 注册hook
            self.fc1.register_forward_hook(self.print_hook('fc1'))
            self.fc2.register_forward_hook(self.print_hook('fc2'))
            self.fc3.register_forward_hook(self.print_hook('fc3'))
        
        def print_hook(self, layer_name):
            def hook(module, input, output):
                print(f"  {layer_name}:")
                print(f"    输入shape: {input[0].shape}")
                print(f"    输出shape: {output.shape}")
                print(f"    输出范围: [{output.min():.3f}, {output.max():.3f}]")
            return hook
        
        def forward(self, x):
            x = F.relu(self.fc1(x))
            x = F.relu(self.fc2(x))
            x = self.fc3(x)
            return x
    
    model = DebugNetwork()
    x = torch.randn(4, 10)
    print("前向传播过程:")
    y = model(x)
    
    # 2. 权重和梯度统计
    print("\n2️⃣ 权重和梯度统计:")
    
    def print_layer_stats(model):
        """打印每层的统计信息"""
        for name, module in model.named_modules():
            if isinstance(module, nn.Linear):
                print(f"\n  {name}:")
                print(f"    权重均值: {module.weight.mean():.4f}")
                print(f"    权重标准差: {module.weight.std():.4f}")
                
                if module.weight.grad is not None:
                    print(f"    梯度均值: {module.weight.grad.mean():.4f}")
                    print(f"    梯度标准差: {module.weight.grad.std():.4f}")
    
    # 执行前向和反向传播
    y = model(x)
    loss = y.mean()
    loss.backward()
    
    print_layer_stats(model)
    
    # 3. 检查数值稳定性
    print("\n3️⃣ 数值稳定性检查:")
    
    def check_numerical_stability(tensor, name="tensor"):
        """检查张量的数值稳定性"""
        has_nan = torch.isnan(tensor).any().item()
        has_inf = torch.isinf(tensor).any().item()
        
        if has_nan or has_inf:
            print(f"  ⚠️ {name} 有数值问题!")
            print(f"    NaN数量: {torch.isnan(tensor).sum().item()}")
            print(f"    Inf数量: {torch.isinf(tensor).sum().item()}")
        else:
            print(f"  ✅ {name} 数值稳定")
            print(f"    范围: [{tensor.min():.4f}, {tensor.max():.4f}]")
            print(f"    均值: {tensor.mean():.4f}")
            print(f"    标准差: {tensor.std():.4f}")
    
    # 测试极端输入
    extreme_input = torch.randn(4, 10) * 1000
    extreme_output = model(extreme_input)
    
    check_numerical_stability(extreme_input, "极端输入")
    check_numerical_stability(extreme_output, "极端输出")

# 运行调试示例
debugging_tips()

🎨 Linear层参数初始化策略

📚 总结与资源 {#总结}

✨ 核心要点回顾

恭喜你完成了这篇超详细的Linear层教程！让我们回顾一下你学到了什么：

1. 理论基础 ✅
  • 理解了从生物神经元到人工神经元的映射
  • 掌握了Linear层的数学本质： y = x W T + b y = xW^T + b y=xWT+b
  • 理解了权重矩阵和偏置的作用
2. 实现细节 ✅
  • 手搓实现了Linear层
  • 理解了前向传播和反向传播
  • 掌握了参数初始化策略
3. 实战应用 ✅
  • 维度变换和投影
  • 分类任务（二分类、多分类、多标签）
  • 自编码器和生成模型
  • Transformer中的应用
4. 优化技巧 ✅
  • 性能优化（数据类型、批处理）
  • 梯度问题处理（消失、爆炸、裁剪）
  • 调试技巧（Hook、统计、稳定性检查）

🎯 关键公式速查

公式 说明 Shape
y = W x + b y = Wx + b y=Wx+b 基本线性变换 [ m ] = [ m , n ] ⋅ [ n ] + [ m ] [m] = [m,n] \cdot [n] + [m] [m]=[m,n]⋅[n]+[m]
Y = X W T + b Y = XW^T + b Y=XWT+b 批量计算 [ B , m ] = [ B , n ] ⋅ [ n , m ] T + [ m ] [B,m] = [B,n] \cdot [n,m]^T + [m] [B,m]=[B,n]⋅[n,m]T+[m]
σ ( W x + b ) \sigma(Wx + b) σ(Wx+b) 带激活函数 保持输出shape
W ∼ U ( − k , k ) W \sim \mathcal{U}(-\sqrt{k}, \sqrt{k}) W∼U(−k ,k ) Xavier初始化 k = 1 / n i n k = 1/n_{in} k=1/nin

💡 最佳实践建议

  1. 初始化选择

    • ReLU激活 → Kaiming初始化
    • Tanh/Sigmoid → Xavier初始化
    • 深层网络 → 考虑正交初始化

  2. 维度设计

    • 逐层递减用于特征提取
    • 瓶颈结构用于压缩
    • 跳跃连接缓解梯度问题

  3. 训练技巧

    • 使用BatchNorm稳定训练
    • 适当的Dropout防止过拟合
    • 梯度裁剪处理梯度爆炸

📖 推荐学习资源

📚 深入学习
🎥 视频课程
  • Stanford CS231n - 卷积神经网络
  • MIT 6.S191 - 深度学习导论
  • Fast.ai - 实用深度学习
💻 实践项目
  1. 入门项目：MNIST手写数字识别
  2. 进阶项目：构建自己的神经网络框架
  3. 研究项目：实现最新的网络架构

🔬 扩展阅读

如果你想更深入地了解Linear层和神经网络：

  1. 理论深入

    • 矩阵微积分和反向传播推导
    • 优化理论（SGD、Adam等）
    • 泛化理论和正则化

  2. 高级话题

    • 稀疏Linear层
    • 量化和剪枝
    • 神经架构搜索（NAS）

  3. 前沿研究

    • Transformer中的Linear层
    • 图神经网络的消息传递
    • 神经常微分方程（Neural ODE）

🙏 结语

Linear层看似简单，实则蕴含深刻的数学原理和工程智慧。它是深度学习的基石，理解它就理解了神经网络的核心。

通过这篇教程，你不仅学会了Linear层的使用，更重要的是理解了它的本质。记住：

"简单的组件，通过巧妙的组合，可以构建出强大的智能系统。"

希望这篇教程对你有所帮助！如果你有任何问题，欢迎在评论区讨论。

Keep Learning, Keep Building! 🚀

🏷️ 标签

PyTorch Linear层 深度学习 神经网络 机器学习 教程 源码解析 实战案例 PlantUML 可视化

最后更新：2025年
字数统计：约50,000字

📝 作者寄语

写这篇教程花费了大量时间和心血，目的是让每一个学习者都能真正理解Linear层。如果这篇文章对你有帮助，请：

  • 👍 点赞支持
  • ⭐ 收藏备用
  • 💬 评论交流
  • 🔄 分享给需要的朋友

你的支持是我创作的最大动力！

相关推荐
说私域2 小时前
基于开源AI智能名片的S2B2C商城小程序中搜索联想功能的优化策略研究
人工智能·小程序
工藤学编程3 小时前
零基础学AI大模型之LangChain聊天模型多案例实战
人工智能·langchain
无风听海3 小时前
神经网络之sigmoid激活函数
人工智能·深度学习·神经网络
宸津-代码粉碎机3 小时前
Redis 进阶：跳出缓存局限！7 大核心场景的原理与工程化实践
java·人工智能·redis·python
wan5555cn3 小时前
AI视频生成技术：从想象到现实的视觉革命
人工智能·笔记·深度学习·算法·音视频
MYZR13 小时前
蓝牙音箱的技术演进：从便捷到高保真的音频革命
人工智能·物联网·音视频·ssd2351
liaomin4161005693 小时前
transformers音频实战01-音频概念
人工智能·音视频
IT_陈寒3 小时前
Python 3.12 性能暴增50%！这5个新特性让老项目直接起飞
前端·人工智能·后端
极客代码3 小时前
第五篇：后端优化——位姿图的灵魂－－从图优化到滑动窗口的联合状态估计
python·深度学习·计算机视觉·视觉里程计·slam·回环检测·地图构建
热门推荐
01OpenSpeedy简介02在国行 macOS 下用 DeepSeek 补齐 Xcode 26 的 AI 能力：问题、原因与 mitmproxy 解决方案（含可用脚本与安装教程）03UV安装并设置国内源04GitHub 镜像站点05UV 工具安装与国内镜像源配置指南06KGG转MP3工具|非KGM文件|解密音频07阿里最新开源Wan2.2-Animate-14B 本地部署教程：统一双模态框架，MoE架构赋能电影级角色动画与替换08Spec-Kit 使用指南09Linux下V2Ray安装配置指南10VsCode远程Copilot无法使用Claude Agent问题