软件设计师——03 数据结构（下）

4 图

4.1 图的定义与存储

4.1.1 图的定义

• 图是一种非线性结构，图中任意两个顶点之间都可能有直接关系，相关定义如下；

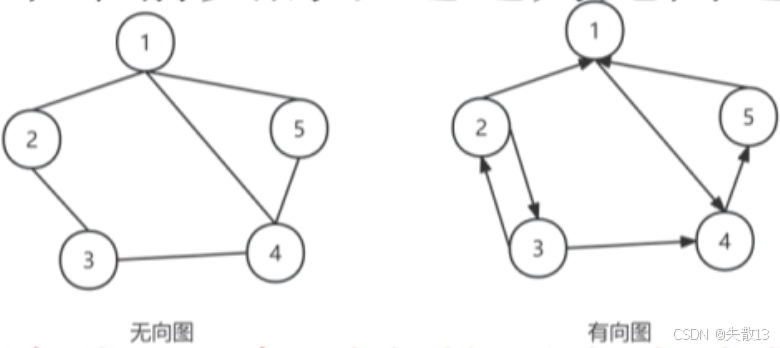
• 有向边和无向边：带箭头的单通道为有向边，不带箭头的双通道为无向边；

• 无向图：图中任意顶点之间均为无向边；

• 有向图：图中任意顶点之间均为有向边；

• 完全图：

  • 无向完全图中，两两顶点之间均有连线，nnn 个顶点的无向完全图有 n(n−1)/2n(n - 1)/2n(n−1)/2 条边；
  • 有向完全图中，两两顶点之间均有连线，nnn 个顶点的有向完全图有 n(n−1)n(n - 1)n(n−1) 条边；

  

• 度、出度和入度：进出某个顶点的边的数目；

  • 其中进入该顶点的边数称为入度 ，从该顶点出去的边数称为出度；
  • 在无向图中，不分入度和出度，有多少条连线就是多少度数；
  • 在有向图中，顶点的度为出度和入度之和；

• 路径：存在一条通路，可以从一个顶点到达另一个顶点，有向图的路径也是有方向的；

• 连通图和连通分量 ：针对无向图；

  • 若从顶点 vvv 到顶点 u 之间是有路径的，则说明 vvv 和 uuu 之间是连通的；
  • 若无向图中任意两个顶点之间都是连通的 ，则称为连通图；
  • 无向图 GGG 的极大连通子图称为其连通分量；

• 强连通图和强连通分量 ：针对有向图；

  • 若有向图中任意两个顶点之间都相互存在路径 ，即存在顶点 vvv 到顶点 uuu，也存在顶点 uuu 到顶点 vvv 的路径，则称为强连通图；
  • 有向图中的极大连通子图称为其强连通分量；

• 生成树 ：一个连通图 的生成树就是该图的连通性不变（即任意两个顶点之间都存在路径），但没有环路的子图 。一个有 nnn 个顶点的生成树有且仅有 n−1n - 1n−1 条边；

• 网：边带权值的图称为网。

4.1.2 图的存储结构

• 邻接矩阵

  • nnn 个顶点的图可以用 n×nn \times nn×n 的邻接矩阵来表示；

  • 若顶点 iii 到顶点 jjj 存在边，则矩阵元素 A[i,j]A[i,j]A[i,j] 的值为 111，否则为 000。通过邻接矩阵可以清晰地反映出图中顶点之间的连接关系；

  

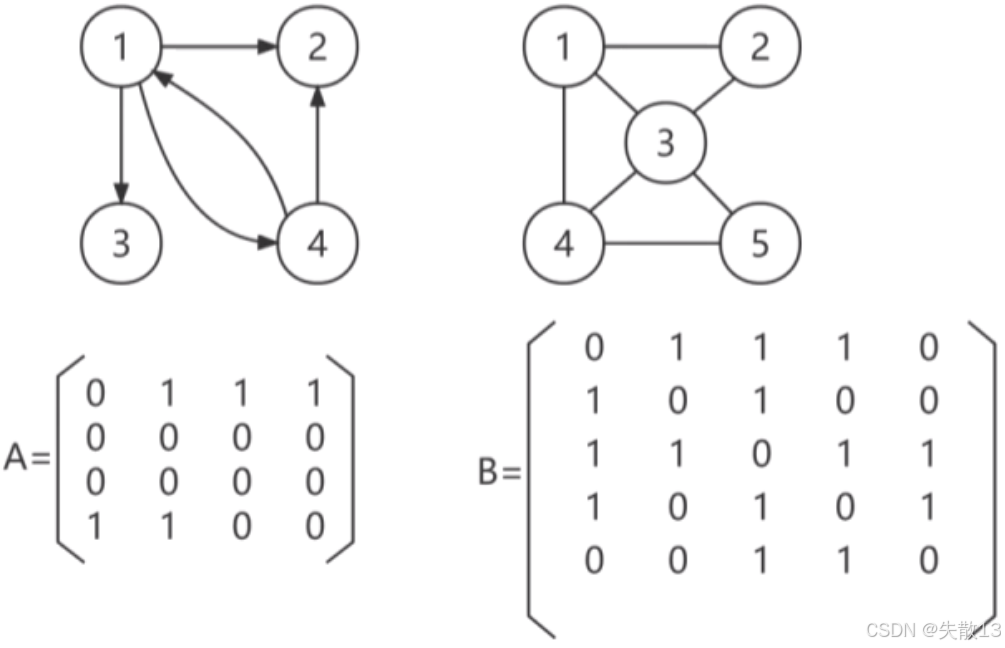
  左图的邻接矩阵 AAA：

  • 顶点数 n=4n = 4n=4，矩阵是 4×44 \times 44×4；
  • 第一行（顶点 111 作为起点）：
    • A[1,2]=1A[1,2] = 1A[1,2]=1：顶点 111 到顶点 222 有向边；
    • A[1,3]=1A[1,3] = 1A[1,3]=1：顶点 111 到顶点 333 有向边；
    • A[1,4]=1A[1,4] = 1A[1,4]=1：顶点 111 到顶点 444 有向边；
  • 第二行（顶点 222 作为起点）：所有元素为 000，说明顶点 222 到其他顶点无有向边；
  • 第三行（顶点 333 作为起点）：所有元素为 000，说明顶点 333 到其他顶点无有向边；
  • 第四行（顶点 444 作为起点）：
    • A[4,1]=1A[4,1] = 1A[4,1]=1：顶点 444 到顶点 111 有向边；
    • A[4,2]=1A[4,2] = 1A[4,2]=1：顶点 444 到顶点 222 有向边；

  右图的邻接矩阵 BBB：

  • 顶点数 n=5n = 5n=5，矩阵是 5\\times 5；
  • 观察对称性（以主对角线为轴）：
    • B[1,2]=B[2,1]=1B[1,2] = B[2,1] = 1B[1,2]=B[2,1]=1：顶点 111 和 222 之间有无向边；
    • B[1,3]=B[3,1]=1B[1,3] = B[3,1] = 1B[1,3]=B[3,1]=1：顶点 111 和 333 之间有无向边；
    • B[1,4]=B[4,1]=1B[1,4] = B[4,1] = 1B[1,4]=B[4,1]=1：顶点 111 和 444 之间有无向边；
    • B[2,3]=B[3,2]=1B[2,3] = B[3,2] = 1B[2,3]=B[3,2]=1：顶点 222 和 333 之间有无向边；
    • B[3,4]=B[4,3]=1B[3,4] = B[4,3] = 1B[3,4]=B[4,3]=1：顶点 333 和 444 之间有无向边；
    • B[3,5]=B[5,3]=1B[3,5] = B[5,3] = 1B[3,5]=B[5,3]=1：顶点 333 和 555 之间有无向边；
    • B[4,5]=B[5,4]=1B[4,5] = B[5,4] = 1B[4,5]=B[5,4]=1：顶点 444 和 555 之间有无向边；

  邻接矩阵通过二维数组直接表示顶点间的连接关系：

  • 有向图的邻接矩阵不一定对称（因为边是单向的）；
  • 无向图的邻接矩阵关于主对角线对称（因为边是双向的）；

• 邻接表

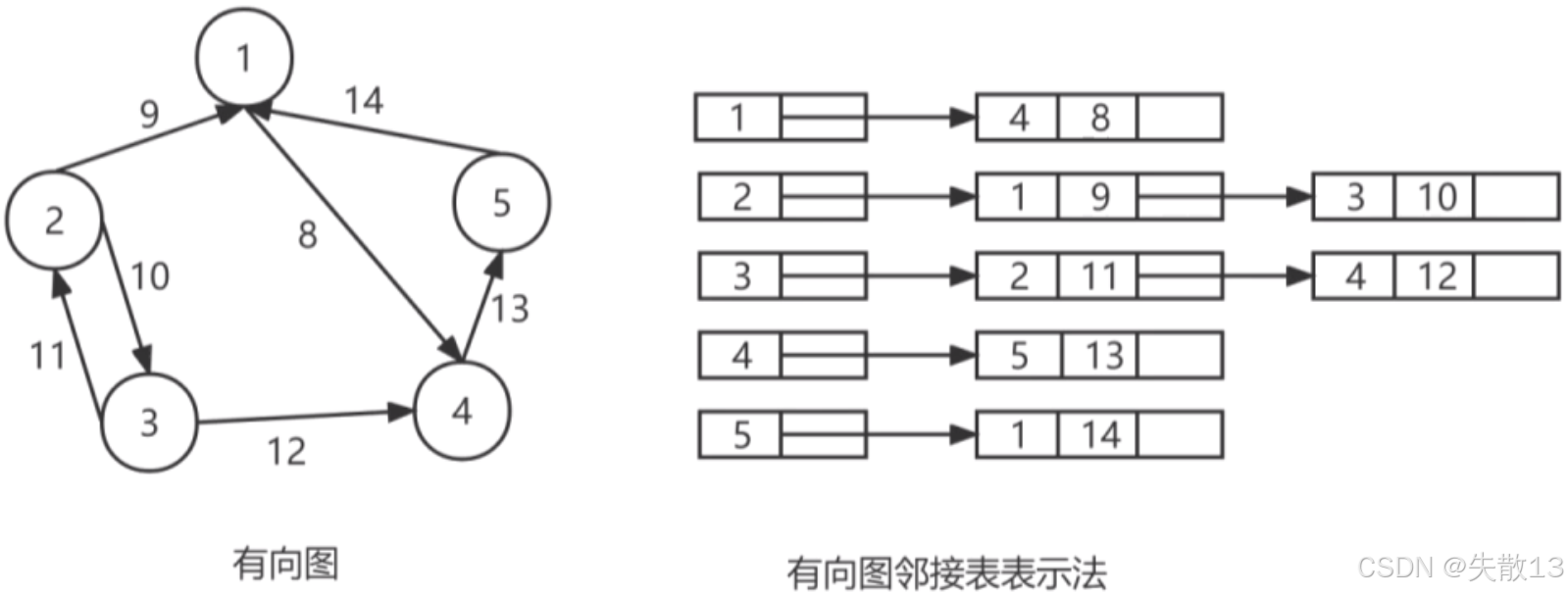
  • 邻接表是链式存储结构；

  • 用一个一维数组存储所有的顶点，对于数组中的每个顶点都生成一个链表；

  • 链表中每个顶点（表节点）包括顶点号、顶点信息（如边的权值）、以及指向下一个顶点的指针。这种存储方式能够灵活地表示图的结构，尤其适合顶点数多但边数少的稀疏图；

  

4.1.3 练习

• 若无向图G有n个顶点e条边，则G采用邻接矩阵存储时，矩阵的大小为（）。

  • A.n∗en*en∗e
  • B.n2n^2n2
  • C.n2+e2n^2 + e^2n2+e2
  • D.(n+e)2(n + e)^2(n+e)2

  B

  n个顶点的图可以用n∗nn*nn∗n的邻接矩阵来表示；

• 某图G的邻接表中共有奇数个表示边的表节点，则图G（）。

  • A.有奇数个顶点
  • B.有偶数个顶点
  • C.是无向图
  • D.是有向图

  D

  在邻接表中，奇数个表示边的表节点说明在图中有奇数条边，无法说明顶点个数是奇数还是偶数，所以A、B选项都是错误的

  由于无向图的边一定是对称存在的，所以表节点的个数一定是偶数，不满足题意，C选项也是错误的。只有D选项符合要求。

4.2 图的遍历

• 图的遍历是从图中的任意一个顶点出发，对图中的所有顶点访问一次且只访问一次。图的遍历分为深度优先搜索 和广度优先搜索两种方式。

4.2.1 深度优先搜索（DFS）

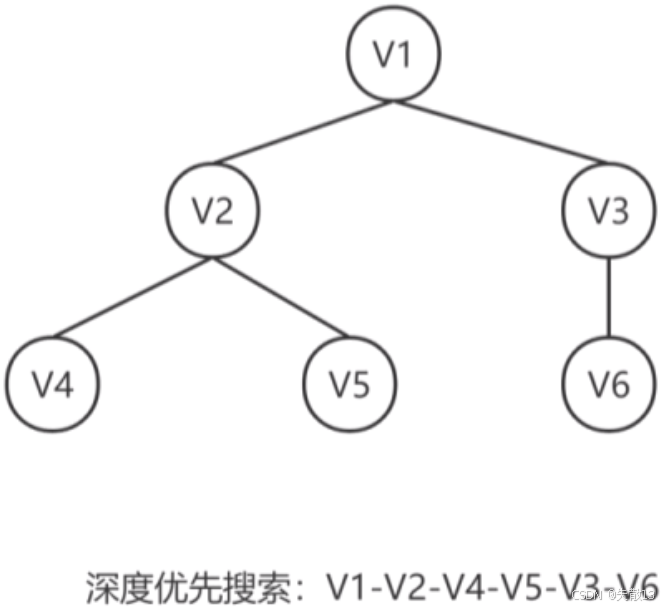
• 特点：类似于树的先根遍历（先访问根节点，再递归访问子树）；

• 步骤：

  • 访问一个顶点 VVV；
  • 依次搜索顶点 VVV 的所有邻接顶点；
  • 若邻接顶点未被访问，则对该邻接顶点进行深度优先搜索；若已被访问，则跳到顶点 VVV 的下一个邻接顶点，重复上述过程，直到所有顶点都被访问；

• 例：

  

4.2.2 广度优先搜索（BFS）

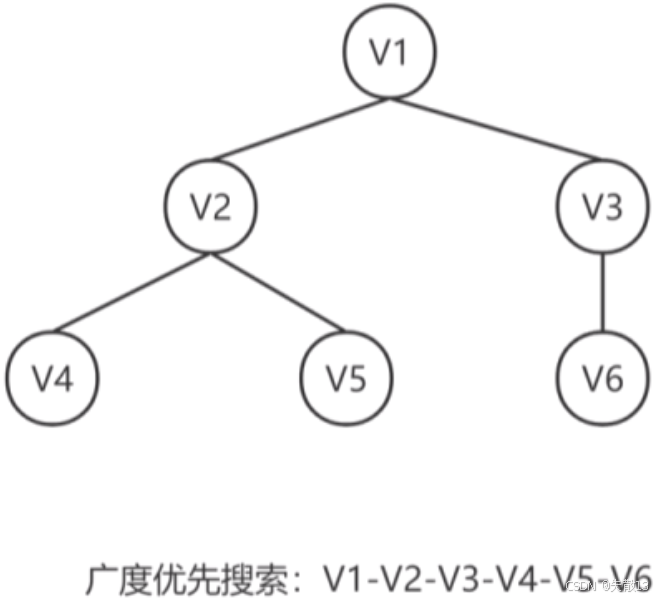
• 特点：类似于树的层次遍历（按层依次访问节点），体现为"深度越小越优先被访问"；

• 步骤：

  • 访问一个顶点 VVV；
  • 依次访问顶点 VVV 的所有未被访问的邻接点；
  • 分别访问这些邻接点的未被访问的所有邻接点，重复此过程，直到所有顶点都被访问。

• 例：

  

4.2.3 时间复杂度

• 使用邻接矩阵 存储图时，两种优先搜索的时间复杂度均为 O(n2)O(n^2)O(n2)（ n 为顶点个数，因为邻接矩阵需遍历每个顶点及对应的行/列判断邻接关系）；
• 使用邻接表 存储图时，两种优先搜索的时间复杂度均为 O(n+e)O(n + e)O(n+e)（nnn 为顶点个数，eee 为边的个数，邻接表只需遍历每个顶点的邻接节点，总邻接节点数与边数相关）。

4.3 生成树和最小生成树

4.3.1 介绍

• 生成树 ：一个连通图 的生成树是该图的连通性不变，但没有环路的子图 。一个有 n 个顶点的生成树有且仅有 n−1n - 1n−1 条边；

• 最小生成树：

  • 包含连通图的所有顶点；

  • 有且仅有 n−1n - 1n−1 条边；

    以上两点就构成了一棵生成树；

  • 这些边的权值总和最小；

  • 注意：最小生成树是一棵树，不是图，且没有环路；

• 求连通带权无向图最小生成树的算法：

  • 普里姆算法（Prim）
  • 克鲁斯卡尔算法（Kruskal）

4.3.2 普里姆算法（Prim）

• 选择一条权值最小的边，并选中该边的顶点，从已选顶点中连接权值最小的边，直至连接所有顶点，且过程中不能出现环路；

• 时间复杂度：O(n2)O(n^2)O(n2)（ n 为顶点个数）；

• 适用场景：只与顶点相关，适用于求稠密图（边数较多的图）的最小生成树；

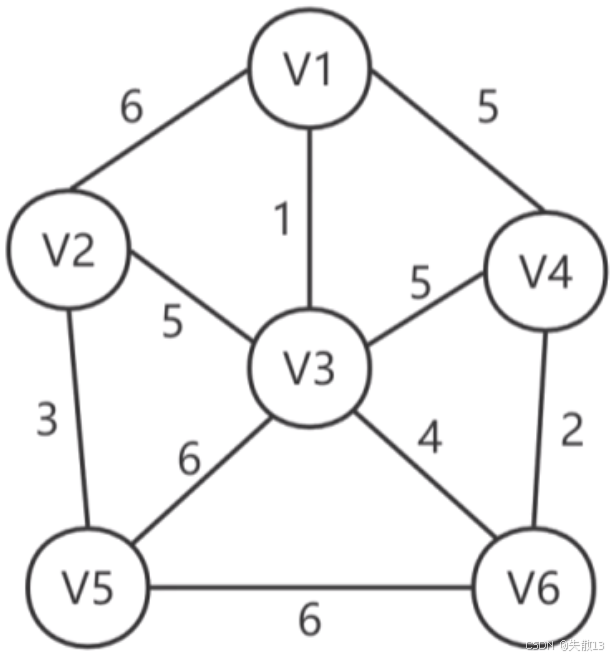
步骤1：初始化

• 设：已选顶点集合 U ，未选顶点集合 V = {V_1, V_2, V_3, V_4, V_5, V_6} ；
• 从 VVV 中找出任意两个顶点之间存在的一条权值最小的边，其中权值最小的边是 V1−V3V_1 - V_3V1−V3（权值 111）；
• 将 V1，V3V_1，V_3V1，V3 加入已选顶点集合 U={V1,V3}U = \{V_1, V_3\}U={V1,V3}，从 VVV 中移除 V3V_3V3，V={V2,V4,V5,V6}V = \{V_2, V_4, V_5, V_6\}V={V2,V4,V5,V6}，记录边 (V_1, V_3) 到最小生成树；

步骤2：第二次选边

• 找出从 U={V1,V3}U = \{V_1, V_3\}U={V1,V3} 到 V={V2,V4,V5,V6}V = \{V_2, V_4, V_5, V_6\}V={V2,V4,V5,V6} 的所有边。这些边有 V1−V2V_1 - V_2V1−V2（权值 666）、V1−V4V_1 - V_4V1−V4（权值 555）、V3−V2V_3 - V_2V3−V2（权值 555）、V3−V4V_3 - V_4V3−V4（权值 555）、V3−V5V_3 - V_5V3−V5（权值 666）、V3−V6V_3 - V_6V3−V6（权值 444）。其中权值最小的边是 V3−V6V_3 - V_6V3−V6（权值 444）；
• 将 V6V_6V6 加入已选顶点集合 U={V1,V3,V6}U = \{V_1, V_3, V_6\}U={V1,V3,V6}，从 VVV 中移除 V6V_6V6，V={V2,V4,V5}V = \{V_2, V_4, V_5\}V={V2,V4,V5}，记录边 (V3,V6)(V_3, V_6)(V3,V6) 到最小生成树；

步骤3：第三次选边

• 找出从 U={V1,V3,V6}U = \{V_1, V_3, V_6\}U={V1,V3,V6} 到 V={V2,V4,V5}V = \{V_2, V_4, V_5\}V={V2,V4,V5} 的所有边。这些边有 V1−V2V_1 - V_2V1−V2（权值 666）、V1−V4V_1 - V_4V1−V4（权值 555）、V3−V2V_3 - V_2V3−V2（权值 555）、V3−V4V_3 - V_4V3−V4（权值 555）、V6−V4V_6 - V_4V6−V4（权值 222）、V6−V5V_6 - V_5V6−V5（权值 666）。其中权值最小的边是 V6−V4V_6 - V_4V6−V4（权值 222）；
• 将 V4V_4V4 加入已选顶点集合 U={V1,V3,V6,V4}U = \{V_1, V_3, V_6, V_4\}U={V1,V3,V6,V4}，从 VVV 中移除 V4V_4V4，V={V2,V5}V = \{V_2, V_5\}V={V2,V5}，记录边 (V6,V4)(V_6, V_4)(V6,V4) 到最小生成树；

步骤4：第四次选边

• 找出从 U={V1,V3,V6,V4}U = \{V_1, V_3, V_6, V_4\}U={V1,V3,V6,V4} 到 V={V2,V5}V = \{V_2, V_5\}V={V2,V5} 的所有边。这些边有 V1−V2V_1 - V_2V1−V2（权值 666）、V3−V2V_3 - V_2V3−V2（权值 555）、V2−V5V_2 - V_5V2−V5（权值 333）、V3−V5V_3 - V_5V3−V5（权值 666）、V6−V5V_6 - V_5V6−V5（权值 666）。其中权值最小的边是 V2−V5V_2 - V_5V2−V5（权值 333）；
• 将 V5V_5V5 加入已选顶点集合 U={V1,V3,V6,V4,V5}U = \{V_1, V_3, V_6, V_4, V_5\}U={V1,V3,V6,V4,V5}，从 VVV 中移除 V5V_5V5，V={V2}V = \{V_2\}V={V2}，记录边 (V2,V5)(V_2, V_5)(V2,V5) 到最小生成树；

步骤5：第五次选边

• 找出从 U={V1,V3,V6,V4,V5}U = \{V_1, V_3, V_6, V_4, V_5\}U={V1,V3,V6,V4,V5} 到 V={V2}V = \{V_2\}V={V2} 的所有边。这些边有 V1−V2V_1 - V_2V1−V2（权值 666）、V3−V2V_3 - V_2V3−V2（权值 555）。其中权值最小的边是 V3−V2V_3 - V_2V3−V2（权值 555）；
• 将 V2V_2V2 加入已选顶点集合 U={V1,V3,V6,V4,V5,V2}U = \{V_1, V_3, V_6, V_4, V_5, V_2\}U={V1,V3,V6,V4,V5,V2}，此时所有顶点都已被访问，记录边 (V3,V2)(V_3, V_2)(V3,V2) 到最小生成树；

最终，最小生成树的边为 (V_1, V_3) （权值 111）、(V3,V6)(V_3, V_6)(V3,V6)（权值 444）、(V6,V4)(V_6, V_4)(V6,V4)（权值 222）、(V2,V5)(V_2, V_5)(V2,V5)（权值 333）、(V3,V2)(V_3, V_2)(V3,V2)（权值 555），权值总和为 1+4+2+3+5=151 + 4 + 2 + 3 + 5 = 151+4+2+3+5=15；

4.3.3 克鲁斯卡尔算法（Kruskal）

• 核心思路：选择权值最小的边进行连接，直至连接所有的顶点，过程中不能出现环路（贪心思想）；

• 时间复杂度：O(elog⁡2e)O(e\log_2 e)O(elog2e)（eee 为边的个数）；

• 适用场景：只与边相关，适用于求稀疏图（边数较少的图）的最小生成树；

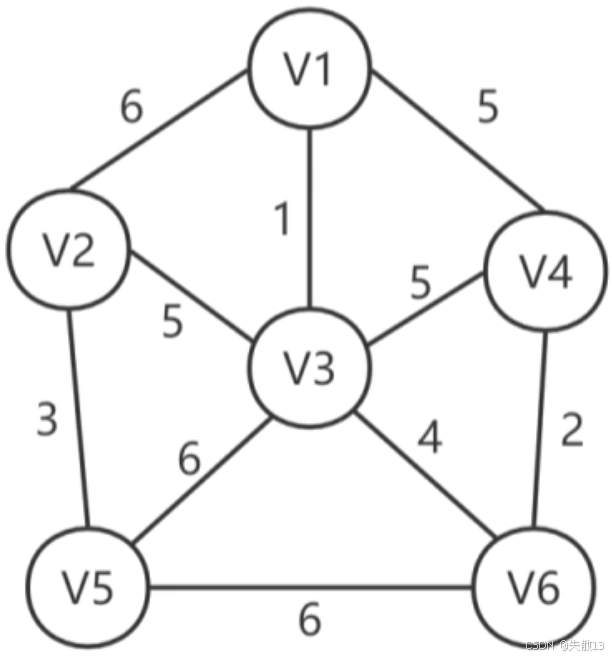
选择边 (V_1, V_3) （权值 111）：此时生成树中的顶点为 V1,V3V_1, V_3V1,V3，无环路；

选择边 (V6,V4)(V_6, V_4)(V6,V4)（权值 222）：生成树中的顶点为 V1,V3,V4,V6V_1, V_3, V_4, V_6V1,V3,V4,V6，无环路；

选择边 (V2,V5)(V_2, V_5)(V2,V5)（权值 333）：生成树中的顶点为 V1,V3,V4,V6,V2,V5V_1, V_3, V_4, V_6, V_2, V_5V1,V3,V4,V6,V2,V5，无环路；

选择边 (V3,V6)(V_3, V_6)(V3,V6)（权值 444）：生成树中的顶点为 V1,V3,V4,V6,V2,V5V_1, V_3, V_4, V_6, V_2, V_5V1,V3,V4,V6,V2,V5，无环路；

选择权值为 555 的边，可以发现有三条，但是要求选择后不能构成环路，所以只能选择边 (V2,V3)(V_2, V_3)(V2,V3)；

最终，最小生成树的边为 (V_1, V_3) （权值 111）、(V6,V4)(V_6, V_4)(V6,V4)（权值 222）、(V2,V5)(V_2, V_5)(V2,V5)（权值 333）、(V3,V6)(V_3, V_6)(V3,V6)（权值 444）、(V3,V2)(V_3, V_2)(V3,V2)（权值 555），权值总和为 1+2+3+4+5=151 + 2 + 3 + 4 + 5 = 151+2+3+4+5=15。

4.4 拓扑排序和关键路径

4.4.1 AOV网和拓扑排序

• AOV（Activity On Vertex NetWork）网定义：如果有向图的顶点表示活动 ，有向边表示活动之间的优先关系，则称这样的图为以顶点表示活动的网（AOV网）；

• 拓扑排序

  • 作用：对AOV网进行拓扑排序，若顶点全部输出，则可以证明AOV网不存在环路；若不能全部输出，则存在环路；

  • 步骤：

    • 在AOV网中选择入度为0的顶点并输出；

    • 从网中删除该顶点及与该顶点有关的弧；

      在有向图中，边也成为"弧"；

    • 重复前两步，直到网中不存在入度为0的顶点为止；

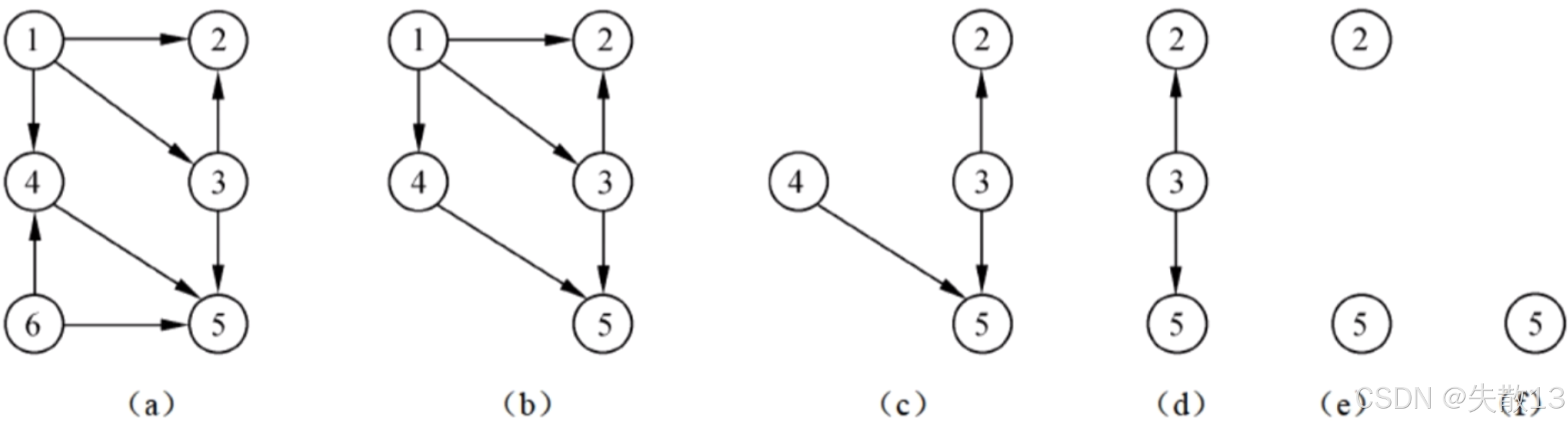
• 示例（结合图中拓扑排序过程图）：

  • 初始图（a）中，入度为0的顶点有1和6，此处选择输出顶点6，删除顶点6及相关弧，得到图（b）；

    也可以选择顶点1。这也体现出了拓扑排序最后输出的结果不是唯一的；

  • 图（b）中入度为0的顶点是1，输出顶点1，删除顶点1及相关弧，得到图（c）；

  • 图（c）中入度为0的顶点是4，输出顶点4，删除顶点4及相关弧，得到图（d）；

  • 图（d）中入度为0的顶点是3，输出顶点3，删除顶点3及相关弧，得到图（e）；

  • 图（e）中入度为0的顶点是5，输出顶点5，删除顶点5及相关弧，得到图（f），所有顶点输出完毕，说明原AOV网无环路；

  

4.4.2 AOE网和关键路径

• AOE（Activity On Edge Network）网定义：如果有向图的顶点表示事件，有向边表示活动，边的权值表示活动持续时间，则这种带权有向图称为以边表示活动的网（AOE网）；

• 关键路径

  • 定义：在从源点（起始事件顶点）到汇点（最终事件顶点）的路径中，长度最长的路径称为关键路径。关键路径上的所有活动均是关键活动；

  • 意义：

    • 如果任何一项关键活动没有按期完成，就会影响整个工程的进度；
    • 缩短关键活动的工期通常可以缩短整个工程的工期；
    • 关键路径上的长度就是完成整个工程项目的最短工期（因为关键路径是最长路径，工程需等最长路径上的活动都完成才能结束）；

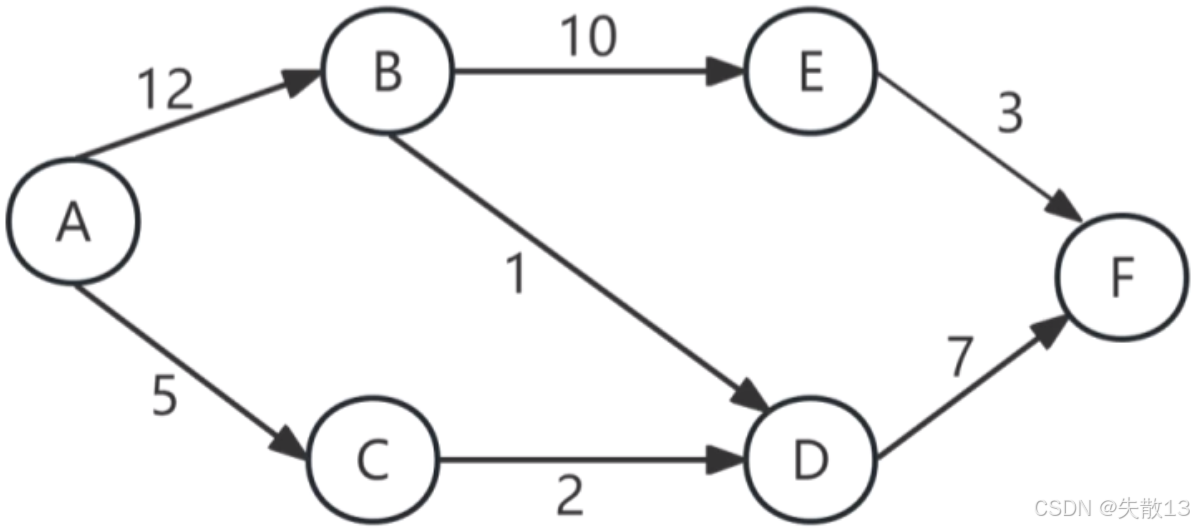
  • 例：需要通过计算各路径的长度，找出最长的那条路径，即为关键路径；

    • 路径 A→B→E→FA \to B \to E \to FA→B→E→F 的长度为 12+10+3=2512 + 10 + 3 = 2512+10+3=25；
    • 路径 A→C→D→FA \to C \to D \to FA→C→D→F 的长度为 5+2+7=145 + 2 + 7 = 145+2+7=14；
    • 路径 A→B→D→FA \to B \to D \to FA→B→D→F 的长度为 12+1+7=2012 + 1 + 7 = 2012+1+7=20；
    • 经比较 A→B→E→FA \to B \to E \to FA→B→E→F 是长度最长的路径，即为关键路径，其长度 252525 就是该工程的最短工期；

  

4.4.3 练习

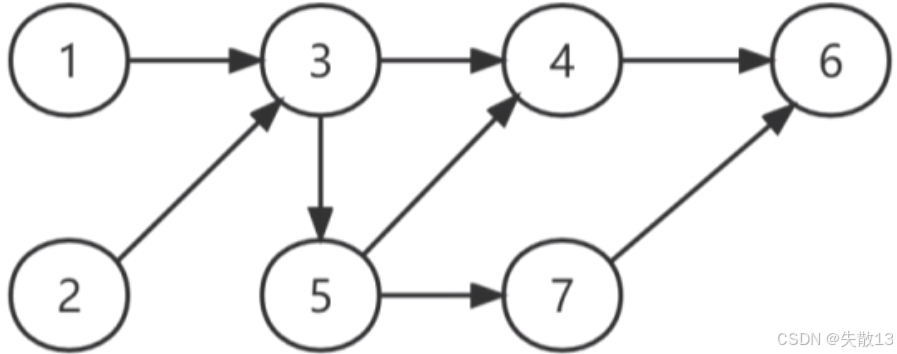
• 拓扑排序是将有向图中所有顶点排成一个线性序列的过程，并且该序列满足：若在AOV网中从顶点到有一条路径，则顶点必然在顶点之前。对于下面的有向图，（）是其拓扑排序。

  • A.1234576
  • B.1235467
  • C.2135476
  • D.2134567

  

  C

  拓扑排序：①在AOV网中选择入度为0的顶点并输出 ②从网中删除该顶点及与该顶点有关的弧 ③重复前两步，直到网中不存在入度为0的顶点为止。

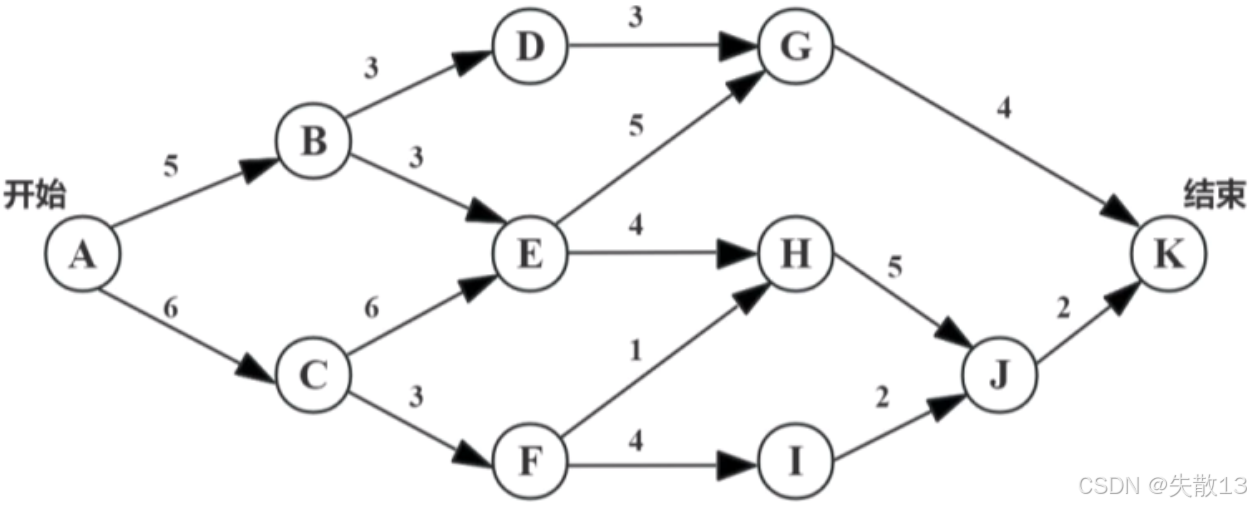
• 下图是一个软件项目的活动图，其中顶点表示项目里程碑，连接顶点的边表示包含的活动，则里程碑（）在关键路径上，关键路径长度为（）。

  • A.B

  • B.E

  • C.G

  • D.I

  • A.15

  • B.17

  • C.19

  • D.23

  

  B D

  关键路径：从开始顶点到结束顶点之间距离最长的一条路径。关键路径上的长度就是完成整个工程项目的最短工期。根据上述项目活动图，路径A - C - E - H - J - K是关键路径，故里程碑E在关键路径上。答案选B D。

4.5 最短路径

• 最短路径的定义：从源点到各顶点最短的路径为最短路径；

4.5.1 迪杰斯特拉（Dijkstra）算法

• 迪杰斯特拉（Dijkstra）算法 ：使用贪心策略解决图的单源最短路径问题，这里的"单源"指的是从一个特定的源点出发，到其他所有顶点的最短路径，该算法属于贪心法范畴；

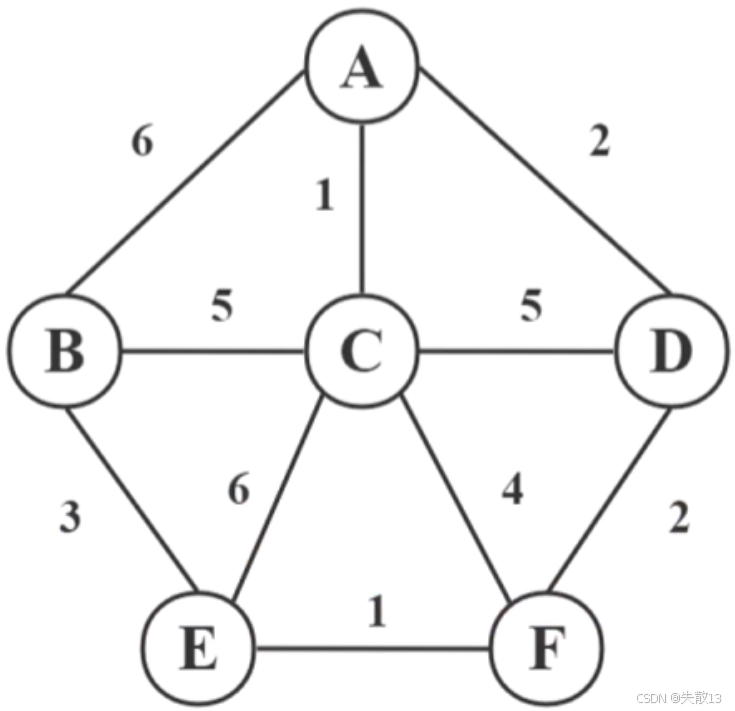
• 以下图为例：求解 A 到 F 的最短路径；

  

• 算法思想：从源点开始，逐步找到到各顶点的最短路径。初始时，源点到自身的距离为0，到其他顶点的距离为无穷大。然后每次选择一个未确定最短路径且距离源点最近的顶点，以该顶点为中间点，更新源点到其他未确定最短路径顶点的距离，直到所有顶点的最短路径都被确定；

  1. 初始化

     • 源点为A，设置距离数组dist，其中dist[A] = 0（源点到自身的距离为0），dist[B] = dist[C] = dist[D] = dist[E] = dist[F] = ∞（源点到其他顶点的距离为无穷大）；

       dist[A]	dist[B]	dist[C]	dist[D]	dist[E]	dist[F]
       0	∞	∞	∞	∞	∞

     • 设置顶点是否已确定最短路径的标记数组visited，初始时所有顶点的visited值为false；

       visited[A]	visited[B]	visited[C]	visited[D]	visited[E]	visited[F]
       false	false	false	false	false	false

  2. 第一次迭代

     • 找到visited为false且dist最小的顶点，即A（dist[A]=0）；

     • 标记A为已访问（visited[A] = true）；

       visited[A]	visited[B]	visited[C]	visited[D]	visited[E]	visited[F]
       true	false	false	false	false	false

     • 以A为中间点 ，更新与A相邻顶点的dist值：

       • A到B的直接距离是6，所以dist[B] = min(∞, 0 + 6) = 6；
       • A到C的直接距离是1，所以dist[C] = min(∞, 0 + 1) = 1；
       • A到D的直接距离是2，所以dist[D] = min(∞, 0 + 2) = 2；

       dist[A]	dist[B]	dist[C]	dist[D]	dist[E]	dist[F]
       0	6	1	2	∞	∞

  3. 第二次迭代

     • 找到visited为false且dist最小的顶点，即C（dist[C]=1）；

     • 标记C为已访问（visited[C] = true）；

       visited[A]	visited[B]	visited[C]	visited[D]	visited[E]	visited[F]
       true	false	true	false	false	false

     • 以C为中间点 ，更新与C相邻顶点的dist值：

       • C到B的直接距离是5，当前dist[B] = 6，1 + 5 = 6，不更新；
       • C到D的直接距离是5，当前dist[D] = 2，1 + 5 = 6，不更新；
       • C到E的直接距离是6，当前dist[E] = ∞，所以dist[E] = 1 + 6 = 7；
       • C到F的直接距离是4，当前dist[F] = ∞，所以dist[F] = 1 + 4 = 5；

       dist[A]	dist[B]	dist[C]	dist[D]	dist[E]	dist[F]
       0	6	1	2	7	5

  4. 第三次迭代

     • 找到visited为false且dist最小的顶点，即D（dist[D]=2）；

     • 标记D为已访问（visited[D] = true）；

       visited[A]	visited[B]	visited[C]	visited[D]	visited[E]	visited[F]
       true	false	true	true	false	false

     • 以D为中间点 ，更新与D相邻顶点的dist值：

       • D到F的直接距离是2，当前dist[F] = 5，2 + 2 = 4，所以dist[F] = min(5, 4) = 4；

       dist[A]	dist[B]	dist[C]	dist[D]	dist[E]	dist[F]
       0	6	1	2	7	4

  5. 第四次迭代

     • 找到visited为false且dist最小的顶点，即F（dist[F]=4）；

       visited[A]	visited[B]	visited[C]	visited[D]	visited[E]	visited[F]
       true	false	true	true	false	true

     • 标记F为已访问（visited[F] = true）。此时，A到F的最短路径长度已确定为4。

4.5.2 弗洛伊德（Floyd）算法

• 弗洛伊德（Floyd）算法 ：使用动态规划的思想解决图的多源点之间最短路径的问题，即可以求出图中任意两个顶点之间的最短路径，该算法属于动态规划法范畴；

• 以下图为例：求解 A 到 F 的最短路径；

  

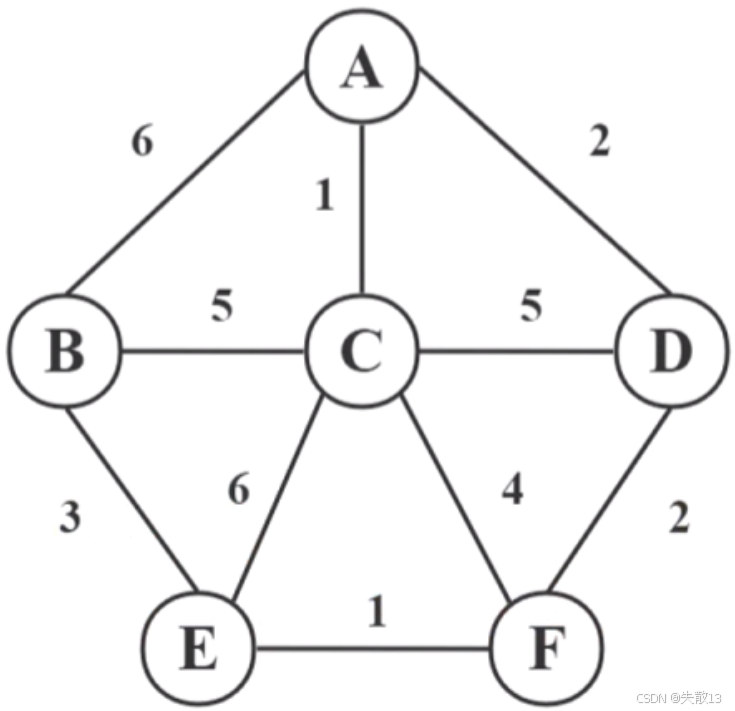
• 算法思想：通过动态规划，逐步考虑中间顶点，更新任意两个顶点之间的最短距离。定义一个距离矩阵dist，其中dist[i][j]表示顶点i到顶点j的直接距离（若无边则为无穷大）。然后，对于每一个中间顶点k，检查dist[i][k] + dist[k][j]是否小于dist[i][j]，如果是，则更新dist[i][j]；

  意思就是说：如果从 i 到 k 的距离 + k 到 j 的距离 < i 到 j 的距离，就更新；

  • 初始化距离矩阵 ：设顶点A、B、C、D、E、F分别用0、1、2、3、4、5表示。初始距离矩阵dist如下（∞表示无穷大）：

    	0（A）	1（B）	2（C）	3（D）	4（E）	5（F）
    0（A）	0	6	1	2	∞	∞
    1（B）	6	0	5	∞	3	6
    2（C）	1	5	0	5	6	4
    3（D）	2	∞	5	0	∞	2
    4（E）	∞	3	6	∞	0	1
    5（F）	∞	6	4	2	1	0

  • 考虑中间顶点k = 0（A） ：对于每对顶点i和j，检查dist[i][0] + dist[0][j]是否小于dist[i][j]。经检查，没有更短的路径，矩阵无更新；

  • 考虑中间顶点k = 1（B） ：对于每对顶点i和j，检查dist[i][1] + dist[1][j]是否小于dist[i][j]。例如：

    • i = 0（A），j = 4（E）：dist[0][1] + dist[1][4] = 6 + 3 = 9，而dist[0][4] = ∞，所以dist[0][4]更新为9；

      即原本dist[0][4] = ∞（A到E的距离是∞），但是dist[0][1] + dist[1][4] = 6 + 3 = 9（A到B + B到E的距离是9），所以更新；

    • 其他顶点对经检查，无更短路径，矩阵部分更新；

    	0（A）	1（B）	2（C）	3（D）	4（E）	5（F）
    0（A）	0	6	1	2	∞	∞
    1（B）	6	0	5	∞	3	6
    2（C）	1	5	0	5	6	4
    3（D）	2	∞	5	0	∞	2
    4（E）	9	3	6	∞	0	1
    5（F）	∞	6	4	2	1	0

  • 考虑中间顶点k = 2（C） ：对于每对顶点i和j，检查dist[i][2] + dist[2][j]是否小于dist[i][j]。例如：

    • i = 0（A），j = 4（E）：dist[0][2] + dist[2][4] = 1 + 6 = 7，比之前的9小，所以dist[0][4]更新为7；
    • i = 0（A），j = 5（F）：dist[0][2] + dist[2][5] = 1 + 4 = 5，dist[0][5]更新为5；
    • 其他顶点对经检查，进行相应更新；

    	0（A）	1（B）	2（C）	3（D）	4（E）	5（F）
    0（A）	0	6	1	2	∞	∞
    1（B）	6	0	5	∞	3	6
    2（C）	1	5	0	5	6	4
    3（D）	2	∞	5	0	∞	2
    4（E）	7	3	6	∞	0	1
    5（F）	5	6	4	2	1	0

  • 考虑中间顶点k = 3（D） ：对于每对顶点i和j，检查dist[i][3] + dist[3][j]是否小于dist[i][j]。例如：

    • i = 0（A），j = 5（F）：dist[0][3] + dist[3][5] = 2 + 2 = 4，比之前的5小，所以dist[0][5]更新为4；

    	0（A）	1（B）	2（C）	3（D）	4（E）	5（F）
    0（A）	0	6	1	2	∞	∞
    1（B）	6	0	5	∞	3	6
    2（C）	1	5	0	5	6	4
    3（D）	2	∞	5	0	∞	2
    4（E）	7	3	6	∞	0	1
    5（F）	4	6	4	2	1	0

  • 考虑中间顶点k = 4（E） ：对于每对顶点i和j，检查dist[i][4] + dist[4][j]是否小于dist[i][j]。经检查，无更短路径，矩阵无更新；

  • 考虑中间顶点k = 5（F） ：对于每对顶点i和j，检查dist[i][5] + dist[5][j]是否小于dist[i][j]。经检查，无更短路径，矩阵无更新；

  • 最终，通过Floyd算法得到A（0）到F（5）的最短路径长度为4。

5 查找

5.1 顺序查找

• 基本思想：从表的一端开始，逐个把表中记录的关键字和给定值做比较。要是有相等的情况，就说明查找成功；要是整个表的记录关键字都和给定值不相等，那查找就失败了；

• 平均查找长度：

  • 公式为 ASL=∑i=1nPiCi=1n(1+2+⋯+n)=n+12ASL = \sum_{i = 1}^{n} P_{i}C_{i} = \frac{1}{n}(1 + 2 + \cdots + n) = \frac{n + 1}{2}ASL=∑i=1nPiCi=n1(1+2+⋯+n)=2n+1，这里的 n 是表中记录的个数；
  • 它表示在顺序查找中，平均需要比较的关键字次数，反映了查找的平均效率；

• 优点：算法很简单，适用范围也广，对表的结构没有要求，表中的记录也不需要是有序的；

• 缺点：当 n 的值比较大的时候，平均查找长度会比较大，查找的效率就比较低。

• 例：假设有一个整数列表 num_list = [5, 12, 3, 9, 18]，现在要查找数字 9 是否在这个列表中；

  • 查找过程：

    • 从列表的第一个元素开始，也就是 5 ，将 5 与要查找的目标值 9 进行比较， 5 != 9，继续查找；

    • 接着看第二个元素 12 ， 12 != 9，继续下一个；

    • 再看第三个元素 3 ， 3 != 9，继续查找。；

    • 然后到第四个元素 9 ， 9 == 9，此时查找成功，找到了目标值在列表中的位置（索引为3的位置） ；

  • 平均查找长度示例：如果列表 num_list = [5, 12, 3, 9, 18] 中每个元素被查找的概率相等，都是 15\frac{1}{5}51；

    • 查找第一个元素 5 时，比较了 1 次；

    • 查找第二个元素 12 时，比较了 2 次；

    • 查找第三个元素 3 时，比较了 3 次；

    • 查找第四个元素 9 时，比较了 4 次；

    • 查找第五个元素 18 时，比较了 5 次；

  • 根据平均查找长度公式 ASL=∑i=1nPiCi=1n(1+2+⋯+n)=n+12ASL = \sum_{i = 1}^{n} P_{i}C_{i} = \frac{1}{n}(1 + 2 + \cdots + n) = \frac{n + 1}{2}ASL=∑i=1nPiCi=n1(1+2+⋯+n)=2n+1 ，这里 n=5n = 5n=5 ，那么 ASL=5+12=3ASL = \frac{5 + 1}{2} = 3ASL=25+1=3 ，意味着平均需要比较3次才能找到目标元素；

  • 如果列表中元素数量增多，比如有 100 个元素，按照公式计算平均查找长度 ASL=100+12=50.5ASL = \frac{100 + 1}{2} = 50.5ASL=2100+1=50.5 ，也就是平均要比较50.5次才能找到目标元素，由此可见，当 nnn 值较大时，顺序查找效率会变低，这也体现了顺序查找的缺点。

5.2 折半（二分）查找

• 折半查找要求表中的元素存储在一维数组（如r[1,⋯ ,n]r[1,\cdots,n]r[1,⋯,n]）中，并且表中元素按递增方式排序。其核心思想是：将给定值 key 与表中中间位置元素与表中中间位置元素与表中中间位置元素r\[mid\]进行比较；

  • 若key==r[mid]key == r[mid]key==r[mid]，则查找成功；

  • 若key>r[mid]key > r[mid]key>r[mid]，说明给定值 key 在后半个子表在后半个子表在后半个子表r\[mid + 1,\\cdots,n\]中，继续对该子表进行折半查找；

  • 若key<r[mid]key < r[mid]key<r[mid]，说明给定值 key 在前半个子表在前半个子表在前半个子表r\[1,\\cdots,mid - 1\]中，继续对该子表进行折半查找；

  • 如此递归，直到查找成功或者子表为空（查找失败）；

• 平均查找长度：公式为ASL=∑i=1nPiCi=1n∑j=1nj×2j−1≈log⁡2(n+1)−1ASL = \sum_{i = 1}^{n} P_{i}C_{i} = \frac{1}{n}\sum_{j = 1}^{n} j\times 2^{j - 1} \approx \log_{2}(n + 1) - 1ASL=∑i=1nPiCi=n1∑j=1nj×2j−1≈log2(n+1)−1，其中nnn为表中记录的个数；

  • 对数函数增长缓慢，所以折半查找平均效率较高；

• 优点：查找效率较高，相比顺序查找，在数据量较大时能大幅减少比较次数；

• 缺点：

  • 要求表采用顺序存储结构，因为折半查找需要通过索引快速定位中间元素，链式存储不便于这样操作；

  • 表中元素必须有序排列，若元素无序，需要先进行排序，而排序本身是有代价的；

  • 插入和删除操作需要移动大量元素，因为要保持元素的有序性，插入或删除一个元素后，可能需要调整其前后元素的位置，当数据量较大时，这会带来较大的开销；

• 折半查找的非递归实现：

  // 接收数组r、查找范围的下界low、上界high以及目标值key
  int Bsearch(int r[], int low, int high, int key) {
      
      int mid;
  
      while (low <= high) {
          // 计算中间位置
          mid = (low + high) / 2;
          // 找到目标值
          if (key == r[mid]) return mid;
          // 目标值在右半部分，将low更新为mid + 1
          else if (key > r[mid]) low = mid + 1;
          // 目标值在左半部分，将high更新为mid - 1
          else high = mid - 1;
      }
      
      // 直到low > high，查找失败
      return -1;
  }

• 折半查找的递归实现：

  int BsearchRecursive(int r[], int low, int high, int key) {
      
      // 递归终止条件：查找范围为空，查找失败
      if (low > high) {
          return -1;
      }
  
      // 计算中间位置
      int mid = (low + high) / 2;
  
      if (key == r[mid]) { // 查找成功，返回位置
          return mid;
      }
      else if (key > r[mid]) { // 目标值在右半部分，递归查找右半部分
          return BsearchRecursive(r, mid + 1, high, key);
      }
      else { // 目标值在左半部分，递归查找左半部分
          return BsearchRecursive(r, low, mid - 1, key);
      }
  }

• 练习：对某有序顺序表进行折半查找（二分查找）时，进行比较的关键字序列不可能是（）。

  • A.42,61,90,85,77
  • B.42,90,85,61,77
  • C.90,85,61,77,42
  • D.90,85,77,61,42

  C

  分析选项C

  • 先与 90 比较，然后再与 85 比较，说明要查找的数比 90 小。此时看看后面的数有没有比 90 大的；

  • 再与 61 比较，说明要查找的数比 85 小。此时看看后面的数有没有比 85 大的；

  • 再与 77 比较，说明要查找的数比 61 大。。此时看看后面的数有没有比 61 小的。有，是42

  • 所以，进行比较的关键字序列不可能是选项C。

5.3 分块查找

• 分块查找又称索引顺序查找，是对顺序查找方法的一种改进，查找效率介于顺序查找和折半查找之间；

• 表的结构：

  • 首先将表分成若干块，每一块内部的关键字不一定有序，但块与块之间是有序的；
  • 另外还建立了一个索引表，索引表按关键字有序排列。每一项包含两部分，一部分是对应块的最大关键字，另一部分是该块在原数据中的起始地址；

  

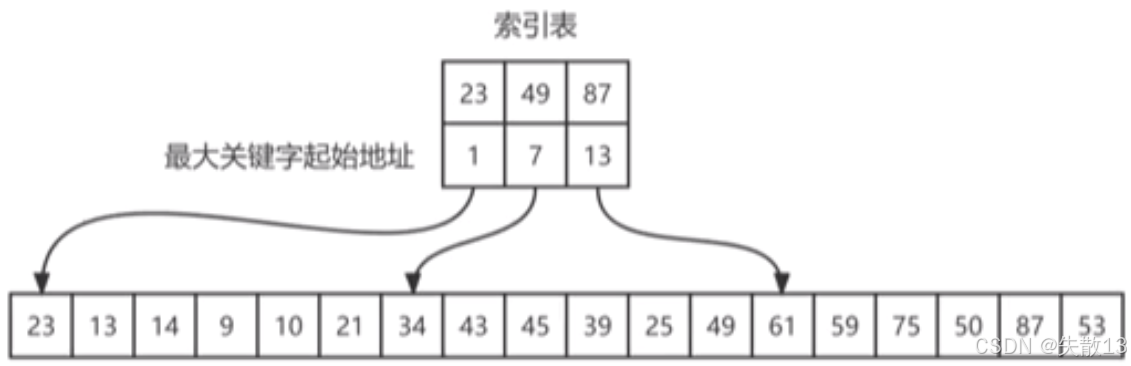
  分块情况：

  • 整个数据被分成了3块；
  • 第一块包含的数据是23、13、14、9、10、21，这一块内部的关键字是无序的，但块与块之间是有序的，即第一块中的最大关键字（23）小于第二块中的最大关键字（49），第二块中的最大关键字（49）小于第三块中的最大关键字（87）；
  • 第二块包含的数据是34、43、45、39、25、49，内部无序，最大关键字49；
  • 第三块包含的数据是61、59、75、50、87、53，内部无序，最大关键字87；

  索引表：

  • 第一行的23、49、87分别是三块的最大关键字；
  • 第二行的1、7、13分别是三块在原数据中的起始位置（从1开始计数）；
  • 比如第一块从位置1开始，包含6个元素（到位置6）；第二块从位置7开始，包含6个元素（到位置12）；第三块从位置13开始，包含6个元素（到位置18）；

• 基本思想：

  • 第一步，在索引表中确定给定值所在的块；
  • 第二步，在确定的块内进行顺序查找；

• 例 ：查找目标：45

  • 在索引表中查找，目标是找到第一个最大关键字大于或等于 45 的块；

    可用顺序查找或折半查找，此处选择顺序查找；

    • **与第一个索引项比较：**因为 45 > 23，所以 45 不可能在第一块，继续查找下一个块；
    • 与第二个索引项比较：因为 45 < 49，这说明 45 可能在第二块中。查找停止，此时确定了要查找的范围是第二块 ，其起始地址是 7；

  • 现在知道 45 可能在地址 7 开始的第二块中，只需要在这个块的范围内进行查找；

    1. 查找地址7的元素： 34。34 != 45，继续；
    2. 查找地址8的元素： 43。43 != 45，继续；
    3. 查找地址9的元素： 45。45 == 45，查找成功；

• 平均查找长度：

  • 公式为 ASL=1b∑j=1bj+1s∑i=1si=b+12+s+12=12(ns+s)+1ASL = \frac{1}{b}\sum_{j = 1}^{b} j + \frac{1}{s}\sum_{i = 1}^{s} i = \frac{b + 1}{2} + \frac{s + 1}{2} = \frac{1}{2}(\frac{n}{s} + s) + 1ASL=b1∑j=1bj+s1∑i=1si=2b+1+2s+1=21(sn+s)+1，其中 bbb 为索引表的大小， sss 为每块记录的个数，表中记录的个数 n=b×sn = b \times sn=b×s；
  • 当 sss 取 n\sqrt{n}n 时， ASLmin=n+1ASL_{min} = \sqrt{n} + 1ASLmin=n +1，此时平均查找长度达到最小值；

  在查找 45 的例子中：

  • 总数据量 nnn ：原数据表共有 181818 个元素；
  • 块的数量 bbb ：数据被分成了 333 块；
  • 每块元素数 sss ：因为 n=b×sn = b \times sn=b×s，所以 s=nb=183=6s = \frac{n}{b} = \frac{18}{3} = 6s=bn=318=6（每块有 666 个元素）；

  索引表查找的平均长度 1b∑j=1bj\frac{1}{b}\sum_{j = 1}^{b} jb1∑j=1bj：

  • 若目标在第 111 块，需比较 111 次；
  • 若目标在第 2 块，需比较 2 次；
  • 若目标在第 3 块，需比较 3 次；
  • 平均下来，索引表查找的平均长度为 1+2+33=3+12=2\frac{1 + 2 + 3}{3} = \frac{3 + 1}{2} = 231+2+3=23+1=2（对应公式 b+12\frac{b + 1}{2}2b+1，b=3b = 3b=3 时，3+12=2\frac{3 + 1}{2} = 223+1=2）；

  块内查找的平均长度 \\frac{1}{s}\\sum_{i = 1}\^{s} i

  • 若目标是块内第 111 个元素，需比较 111 次；
  • 若目标是块内第 2 个元素，需比较 2 次；
  • ......
  • 若目标是块内第 666 个元素，需比较 666 次；
  • 平均下来，块内查找的平均长度为 1+2+⋯+66=6+12=3.5\frac{1 + 2 + \cdots + 6}{6} = \frac{6 + 1}{2} = 3.561+2+⋯+6=26+1=3.5（对应公式 s+12\frac{s + 1}{2}2s+1，s = 6 时，时，时，\\frac{6 + 1}{2} = 3.5）；

  总平均查找长度 ASLASLASL

  • 将两部分相加，总平均查找长度为：
    ASL=索引表平均长度+块内平均长度=2+3.5=5.5 ASL = \text{索引表平均长度} + \text{块内平均长度} = 2 + 3.5 = 5.5 ASL=索引表平均长度+块内平均长度=2+3.5=5.5

  • 用公式计算验证：
    ASL=12(ns+s)+1=12(186+6)+1=12(3+6)+1=4.5+1=5.5 ASL = \frac{1}{2}\left( \frac{n}{s} + s \right) + 1 = \frac{1}{2}\left( \frac{18}{6} + 6 \right) + 1 = \frac{1}{2}(3 + 6) + 1 = 4.5 + 1 = 5.5 ASL=21(sn+s)+1=21(618+6)+1=21(3+6)+1=4.5+1=5.5

  • 结果一致；

  最小平均查找长度

  • 当 s = \\sqrt{n} 时，ASLASLASL 达到最小值 \\sqrt{n} + 1 ；

  • 在例子中，n=18n = 18n=18，则 18≈4.24\sqrt{18} \approx 4.2418 ≈4.24。若每块元素数 sss 取 444 或 555（接近 18\sqrt{18}18 ），重新分块后，平均查找长度会比当前 5.55.55.5 更小。

  总结：分块查找的平均查找长度，是"索引表查找的平均次数"与"块内查找的平均次数"之和，且可通过调整每块元素数 sss 来优化总效率；

• 优点：查找效率好于顺序查找，能够通过索引表快速确定给定值所在的块；

• 缺点：查找效率不及折半查找。

5.4 哈希表

5.4.1 介绍

• 前面的顺序查找、折半查找、分块查找都是以关键字比较为基础，而哈希表（也称为散列表）不同，它通过计算以记录的关键字为自变量的函数（哈希函数）来得到该记录的存储地址。在查找操作时，用同一哈希函数 H(key) 计算待查记录的存储地址，到相应的存储单元中匹配信息来判定是否查找成功；

• 哈希函数的构造方法：有直接定址法、数字分析法、平方取中法、折叠法、随机数法、除留余数法等；

  直接定址法

  • 取关键字或关键字的某个线性函数值为哈希地址，即 H(key)=a×key+bH(key)=a \times key + bH(key)=a×key+b（ a 、、、b 为常数）；

  • 示例 ：假设要对一个小型的学生成绩管理系统中的学生成绩进行哈希存储，学生的学号是从 1000−10991000 - 10991000−1099，我们可以直接把学号作为哈希地址，即 H(key)=keyH(key) = keyH(key)=key 。比如学号为 102310231023 的学生成绩，就直接存放在哈希表的第 102310231023 个位置；

  数字分析法

  • 数字分析法是对关键字进行分析，找出其中分布均匀的若干位作为哈希地址；

  • 示例 ：假设有一组关键字是 10 位的号码，如 881234567888123456788812345678、882345678988234567898823456789 、883456789088345678908834567890 等，前两位都是 888888 ，最后两位分布也不均匀，而中间的 123412341234、234523452345、345634563456 等分布相对均匀，就可以取中间的 444 位作为哈希地址。比如对于 881234567888123456788812345678 ，其哈希地址 H(key)=1234H(key) = 1234H(key)=1234 ；

  平方取中法

  • 先求出关键字的平方值，然后按需要取平方值的中间若干位作为哈希地址；

  • 示例 ：假设关键字 key=43key = 43key=43 ，先计算 432=184943^2 = 1849432=1849 ，如果需要一个两位的哈希地址，就取中间的 848484 ，即 H(key)=84H(key)=84H(key)=84 ；

  折叠法

  • 将关键字分割成位数相同的几部分（最后一部分的位数可以不同），然后取这几部分的叠加和（舍去进位）作为哈希地址；

  • 示例 ：假设关键字 key=1234567890key = 1234567890key=1234567890 ，把它分成 123123123、456456456、789789789、000 这几部分 ，然后计算 123+456+789+0=1368123 + 456 + 789 + 0 = 1368123+456+789+0=1368 ，舍去进位后，取 368368368 作为哈希地址，即 H(key)=368H(key)=368H(key)=368 ；

  随机数法

  • 选择一个随机函数，取关键字的随机函数值为它的哈希地址，即 H(key)=random(key)H(key) = random(key)H(key)=random(key) ，其中 randomrandomrandom 为随机函数；

  • 示例 ：在一个需要对游戏角色ID进行哈希存储的场景中，可以使用编程语言自带的随机函数库来实现。假设游戏角色ID是从 1 - 10000 ，在Python中使用 random 库，如 import random ，然后定义 H(key) = random.randint(0, 999) （这里假设哈希表大小为 1000 ），比如角色ID为 345634563456 ，通过这个哈希函数可能得到的哈希地址是 123123123 （每次运行结果会不同，因为是随机的）；

  除留余数法

  • 取关键字被某个不大于哈希表表长 mmm 的数 ppp 除后所得的余数为哈希地址，即 H(key)=key%pH(key)=key \% pH(key)=key%p ，p≤mp\leq mp≤m ，并且 ppp 应尽量取质数；
  • 示例 ：假设哈希表表长 m=11m = 11m=11 ，要对一组整数关键字进行哈希存储，对于关键字 key=25key = 25key=25 ，则 H(key)=25%11=3H(key)=25 \% 11 = 3H(key)=25%11=3 ；对于关键字 key=37key = 37key=37 ，则 H(key)=37%11=4H(key)=37 \% 11 = 4H(key)=37%11=4 ；

• 处理冲突的方法：对于不同的关键字，却有相同的哈希函数值，这种情况称为冲突。解决冲突就是为出现冲突的关键字找到另一个尚未使用的哈希地址。常见的处理冲突的方法有：

  • 开放定址法
  • 链地址法

5.4.2 开放定址法

• 公式为Hi=(H(key)+di)%m,i=1,2,⋯ ,k(k≤m−1)H_{i}=(H(key)+d_{i})\%m, i = 1,2,\cdots,k(k\leq m - 1)Hi=(H(key)+di)%m,i=1,2,⋯,k(k≤m−1)，其中HiH_{i}Hi为哈希地址，H(key)H(key)H(key)为哈希函数，mmm为哈希表表长，did_{i}di为增量序列；

• 常见的增量序列有以下三种：

  • di=1,2,⋯ ,m−1d_{i}=1,2,\cdots,m - 1di=1,2,⋯,m−1，称为线性探测再散列；

  • di=12,−12,22,−22,⋯ ,±k2(k≤m2)d_{i}=1^{2},-1^{2},2^{2},-2^{2},\cdots,\pm k^{2}(k\leq\frac{m}{2})di=12,−12,22,−22,⋯,±k2(k≤2m)，称为二次探测再散列；

  • did_{i}di为伪随机数序列，称为随机探测再散列；

  例：假设哈希表表长 m=11m = 11m=11，哈希函数 H(key)=key%11H(key) = key \% 11H(key)=key%11，现在要插入关键字 key=12key = 12key=12，计算初始哈希地址 H(12)=12%11=1H(12) = 12 \% 11 = 1H(12)=12%11=1，但地址 111 已经被占用（比如已存有关键字 111），此时需要用开放定址法解决冲突；

  线性探测再散列（di=1,2,⋯ ,m−1d_i = 1,2,\cdots,m - 1di=1,2,⋯,m−1）

  • 当第一次计算的哈希地址 H0=1H_0 = 1H0=1 被占用时，按照线性探测再散列的规则，增量 d1=1d_1 = 1d1=1，计算下一个哈希地址 H1=(H(12)+d1)%m=(1+1)%11=2H_1=(H(12)+d_1)\%m=(1 + 1)\%11 = 2H1=(H(12)+d1)%m=(1+1)%11=2；
  • 如果地址 222 仍被占用，增量 d2=2d_2 = 2d2=2，计算 H2=(1+2)%11=3H_2=(1 + 2)\%11 = 3H2=(1+2)%11=3，以此类推，直到找到一个空闲的地址；

  二次探测再散列（di=12,−12,22,−22,⋯ ,±k2(k≤m2)d_i = 1^2,-1^2,2^2,-2^2,\cdots,\pm k^2(k\leq\frac{m}{2})di=12,−12,22,−22,⋯,±k2(k≤2m)）

  • 同样初始哈希地址 H0=1H_0 = 1H0=1 被占用，首先取 d1=12=1d_1 = 1^2 = 1d1=12=1，计算 H1=(1+1)%11=2H_1=(1 + 1)\%11 = 2H1=(1+1)%11=2；
  • 若地址 222 被占用，取 d2=−12=−1d_2 = -1^2 = -1d2=−12=−1，计算 H2=(1−1)%11=0H_2=(1 - 1)\%11 = 0H2=(1−1)%11=0；
  • 若地址 000 被占用，取 d3=22=4d_3 = 2^2 = 4d3=22=4，计算 H3=(1+4)%11=5H_3=(1 + 4)\%11 = 5H3=(1+4)%11=5；
  • 若地址 555 被占用，取 d4=−22=−4d_4 = -2^2 = -4d4=−22=−4，计算 H4=(1−4)%11=8H_4=(1 - 4)\%11 = 8H4=(1−4)%11=8（因为 (1−4)=−3(1 - 4) = -3(1−4)=−3，−3%11=8-3 \% 11 = 8−3%11=8，在取模运算中，负数取模结果为正数，等于模数加上该负数对模数取余的结果），依此类推，直到找到空闲地址；

  随机探测再散列（did_idi 为伪随机数序列）

  • 假设有一个伪随机数生成器，生成的伪随机数序列为 3,5,2,⋯3, 5, 2, \cdots3,5,2,⋯
  • 初始哈希地址 H0=1H_0 = 1H0=1 被占用，取第一个伪随机数 d1=3d_1 = 3d1=3，计算 H1=(1+3)%11=4H_1=(1 + 3)\%11 = 4H1=(1+3)%11=4；
  • 若地址 444 被占用，取第二个伪随机数 d_2 = 5 ，计算 H_2=(1 + 5)%11 = 6 ；
  • 若地址 666 被占用，取第三个伪随机数 d_3 = 2 ，计算 H_3=(1 + 2)%11 = 3 ，以此类推，直到找到空闲地址；

• 练习：

  

  • 哈希函数为 Hash(key)=keymod  11Hash(key) = key \mod 11Hash(key)=keymod11，计算每个关键字的初始哈希地址：

    关键字	keymod  11key \mod 11keymod11	初始哈希地址
    47	47mod  11=347 \mod 11 = 347mod11=3	3
    34	34mod  11=134 \mod 11 = 134mod11=1	1
    13	13mod  11=213 \mod 11 = 213mod11=2	2
    12	12mod  11=112 \mod 11 = 112mod11=1	1
    52	52mod  11=852 \mod 11 = 852mod11=8	8
    38	38mod  11=538 \mod 11 = 538mod11=5	5
    33	33mod  11=033 \mod 11 = 033mod11=0	0
    27	27mod  11=527 \mod 11 = 527mod11=5	5
    3	3mod  11=33 \mod 11 = 33mod11=3	3

  • 用线性探测再散列解决冲突，构造哈希表

    • 插入 47。初始地址 333 为空，直接插入。哈希表地址 333：关键字 47 ，查找次数 111。

    • 插入 34。初始地址 111 为空，直接插入。哈希表地址 111：关键字 34 ，查找次数 111；

    • 插入 13。初始地址 222 为空，直接插入。哈希表地址 222：关键字 13 ，查找次数 111；

    • 插入 12

      • 初始地址 111 已被 343434 占用（冲突），探测下一个地址 (1+1)mod  11=2(1 + 1) \mod 11 = 2(1+1)mod11=2，地址 222 已被 131313 占用（冲突），继续探测下一个地址 (1+2)mod  11=3(1 + 2) \mod 11 = 3(1+2)mod11=3，地址 333 已被 474747 占用（冲突），继续探测下一个地址 (1+3)mod  11=4(1 + 3) \mod 11 = 4(1+3)mod11=4，地址 444 为空，插入；
      • 哈希表地址 444：关键字 121212，查找次数 444（探测了 1,2,3,41,2,3,41,2,3,4，共 444 次）；

    • 插入 5。初始地址 888 为空，直接插入。哈希表地址 888：关键字 525252，查找次数 111；

    • 插入 38。初始地址 555 为空，直接插入。哈希表地址 555：关键字 383838，查找次数 111；

    • 插入 33。初始地址 000 为空，直接插入。哈希表地址 000：关键字 333333，查找次数 111；

    • 插入 27

      • 初始地址 555 已被 383838 占用（冲突），探测下一个地址 (5+1)mod  11=6(5 + 1) \mod 11 = 6(5+1)mod11=6，地址 666 为空，插入；

      • 哈希表地址 666：关键字 27 ，查找次数 222（探测了 5,6 ，共 222 次）；

    • 插入 3

      • 初始地址 333 已被 474747 占用（冲突），探测下一个地址 (3+1)mod  11=4(3 + 1) \mod 11 = 4(3+1)mod11=4，地址 444 已被 121212 占用（冲突），继续探测下一个地址 (3+2)mod  11=5(3 + 2) \mod 11 = 5(3+2)mod11=5，地址 555 已被 383838 占用（冲突），继续探测下一个地址 (3+3)mod  11=6(3 + 3) \mod 11 = 6(3+3)mod11=6，地址 666 已被 272727 占用（冲突），继续探测下一个地址 (3+4)mod  11=7(3 + 4) \mod 11 = 7(3+4)mod11=7，地址 777 为空，插入；

      • 哈希表地址 777：关键字 333，查找次数 555（探测了 3,4,5,6,73,4,5,6,73,4,5,6,7，共 555 次）；

  • 构造最终的哈希表

    哈希地址	0	1	2	3	4	5	6	7	8	9	10
    关键字	33	34	13	47	12	38	27	3	52	空	空

  • 计算平均查找长度（ASL）

    • 平均查找长度 ASL=总查找次数关键字个数ASL = \frac{\text{总查找次数}}{\text{关键字个数}}ASL=关键字个数总查找次数；

    • 总查找次数为：1+1+1+4+1+1+2+5=161 + 1 + 1 + 4 + 1 + 1 + 2 + 5 = 161+1+1+4+1+1+2+5=16（每个关键字的查找次数相加）；

    • 关键字个数为 999；

    • 因此，ASL=169≈1.78ASL = \frac{16}{9} \approx 1.78ASL=916≈1.78。

5.4.3 链地址法

• 将冲突的元素存放在一个链表中，通过链表查找冲突的数据元素；

• 以上一节的练习为例：

  • 哈希地址为111的位置，有343434和121212两个元素冲突，就通过链表将它们连接起来；
  • 哈希地址为333的位置，474747和333冲突，也通过链表连接；
  • 哈希地址为555的位置，383838和272727冲突，同样用链表连接；

  哈希地址 指针 哈希地址0 33 哈希地址1 34 12 哈希地址2 13 哈希地址3 47 3 哈希地址4 哈希地址5 38 27 哈希地址6 哈希地址7 哈希地址8 52 哈希地址9 哈希地址10

• 其它处理哈希冲突的方法：

  • 再哈希法

  • 建立一个公共溢出区

6 排序

• 排序的定义 ：将任意排列的一组元素变成一组有序排列（递增或递减）的元素；

• 排序的分类：

  • 稳定排序与不稳定排序：待排元素中的相同值在排序后的次序关系不变，这样的排序称为稳定排序，否则为不稳定排序；

    比如9 7 5 6 5排序后变成5 5 6 7 9；

    排序前在前面的5在排序后仍在前面，排序后在后面的5仍在后面，就是稳定排序；

  • 内排序和外排序：排序在内存中进行的称为内排序，在外存中进行的称为外排序。

6.1 直接插入排序

• 将待排元素插入到有序序列 的合适位置中，是一种稳定的排序方法；
• 排序步骤 ：在插入第iii个记录时，R1,R2,⋯ ,Ri−1R_1, R_2, \cdots, R_{i - 1}R1,R2,⋯,Ri−1均已排好序，此时将第iii个记录依次与Ri−1,⋯ ,R2,R1R_{i - 1}, \cdots, R_2, R_1Ri−1,⋯,R2,R1进行比较，找到合适的位置插入，插入位置及其之后的记录依次向后移动；
• 时间复杂度 ：
  • 最好情况：元素已经是正序排列，此时每次插入只需要比较111次，时间复杂度为O(n)O(n)O(n)；
  • 最坏情况：元素是逆序排列，此时每次插入需要比较iii次（iii从222到nnn），时间复杂度为O(n2)O(n^2)O(n2)；
• 空间复杂度 ：只需要一个临时变量记录待排元素的值（哨兵），空间复杂度为O(1)O(1)O(1)。

6.2 希尔排序

• 希尔排序是对直接插入排序的改进，本质是一种分组插入排序 ，是一种不稳定的排序方法；

• 基本思想：将待排元素按一定"增量"进行分组，然后对每个分组分别进行直接插入排序；随着增量的减小，一直到增量为111，从而使整个序列变得有序；

• 增量的取值：增量序列通常取d1=n/2,d2=d1/2,d3=d2/2,⋯ ,di=1d_1 = n/2, d_2 = d_1/2, d_3 = d_2/2, \cdots, d_i = 1d1=n/2,d2=d1/2,d3=d2/2,⋯,di=1（nnn为待排序元素个数）；

• 时间复杂度：约为O(n1.3)O(n^{1.3})O(n1.3)，相比直接插入排序，在数据量较大时，效率有明显提升；

• 空间复杂度：仅需要一个元素的辅助空间，空间复杂度为O(1)O(1)O(1)；

• 例：将下面的数据通过希尔排序，得到一个从小到大排列的序列

  49	38	65	97	76	13

  • 第1趟希尔排序（增量d1=6/2=3d_1 = 6/2 = 3d1=6/2=3）：

    • 按增量333分组，将元素分为333组，每组元素下标相差333：
      • 第1组：49（下标000）、97（下标333）；
      • 第2组：38（下标 1 ）、'76'（下标）、\`76\`（下标）、'76'（下标 4 ）；
      • 第3组：65（下标222）、13（下标555）；
    • 对每组分别进行直接插入排序：
      • 第1组49、97，已有序，无需调整；
      • 第2组38、76，已有序，无需调整；
      • 第3组65、13，排序后变为13、65；
    • 此时序列变为49、38、13、97、76、65；

  • 第2趟希尔排序（增量d_2 = 3/2 = 2 ）：

    • 按增量 2 分组，将元素分为分组，将元素分为分组，将元素分为 2 组，每组元素下标相差组，每组元素下标相差组，每组元素下标相差 2 ：
      • 第1组：49（下标 0 ）、'13'（下标）、\`13\`（下标）、'13'（下标 2 ）、'76'（下标）、\`76\`（下标）、'76'（下标 4 ）；
      • 第2组：38（下标111）、97（下标333）、65（下标555）；
    • 对每组分别进行直接插入排序：
      • 第1组49、13、76，排序后变为13、49、76；
      • 第2组38、97、65，排序后变为38、65、97；
    • 此时序列变为13、38、49、65、76、97；

  • 第3趟希尔排序（增量d_3 = 2/2 = 1 ） ：增量为111，此时整个序列作为一组，进行直接插入排序。由于经过前两趟排序，序列已基本有序，直接插入排序效率很高，最终得到有序序列13、38、49、65、76、97。

6.3 冒泡排序

• 冒泡排序是交换排序的一种，是一种稳定的排序方法；

• 基本思想：两两比较待排元素，若次序相反，则交换位置，直到整个序列没有反序。它是通过相邻元素之间的比较和交换，将最大元素（或最小元素）交换到顶层的位置上；

• 时间复杂度：为O(n2)O(n^2)O(n2)，其中nnn是待排序元素的个数，在最坏情况下（元素完全逆序），需要进行n−1n - 1n−1趟排序，每趟进行 n - i 次比较（次比较（次比较（i为趟数）；

• 空间复杂度：仅需要一个元素的辅助空间用于交换元素，空间复杂度为O(1)O(1)O(1)；

• 例：将序列49、38、65、97、76、13从小到大排序

  • 第1趟冒泡排序：

    • 从第一个元素开始，依次比较相邻的两个元素：
      • 比较49和38，因为 49 \> 38 ，次序相反，交换它们的位置，序列变为38、49、65、97、76、13；
      • 接着比较49和65，49<6549 < 6549<65，次序正确，不交换；
      • 比较65和97，65<9765 < 9765<97，次序正确，不交换；
      • 比较97和76，97>7697 > 7697>76，次序相反，交换位置，序列变为38、49、65、76、97、13；
      • 比较97和13，97>1397 > 1397>13，次序相反，交换位置，序列变为38、49、65、76、13、97；
    • 经过第1趟排序，最大的元素97被交换到了最后一位（顶层位置）；

  • 第2趟冒泡排序：

    • 此时待排序的元素是前 5 个（38、49、65、76、13），继续从第一个元素开始相邻比较：
      • 比较38和49， 38 \< 49 ，次序正确，不交换；
      • 比较49和65， 49 \< 65 ，次序正确，不交换；
      • 比较65和76， 65 \< 76 ，次序正确，不交换；
      • 比较76和13， 76 \> 13 ，次序相反，交换位置，序列变为38、49、65、13、76、97；
    • 这一趟排序后，第二大的元素76被交换到了倒数第二位；

  • 后续趟数（补充完整过程）：

    • 第3趟冒泡排序 ：待排序元素为前444个（38、49、65、13）。经过比较交换，会将65交换到倒数第三位，序列变为38、49、13、65、76、97；
    • 第4趟冒泡排序 ：待排序元素为前333个（38、49、13）。经过比较交换，会将49交换到倒数第四位，序列变为38、13、49、65、76、97；
    • 第5趟冒泡排序 ：待排序元素为前222个（38、13）。比较后交换，得到13、38、49、65、76、97，此时整个序列有序；

  • 通过多趟相邻元素的比较与交换，逐步将大的元素"冒泡"到序列的末尾，最终使整个序列有序；

• 代码：

  void BubbleSort(int arr[], int n) {
      
      // 外层循环控制排序趟数，共需 n-1 趟
      for (int i = 0; i < n - 1; i++) {
          // 内层循环负责每趟比较和交换
          for (int j = 0; j < n - 1 - i; j++) {
              // 每次比较相邻元素
              if (arr[j] > arr[j + 1]) {
                  // 若逆序则交换
                  int temp = arr[j];
                  arr[j] = arr[j + 1];
                  arr[j + 1] = temp;
              }
          }
      }
  }

• 优化代码：增加 swapped 标志位，检测是否发生交换。若某趟排序未发生任何交换，说明数组已完全有序，可提前终止循环

  void BubbleSortOptimized(int arr[], int n) {
      
      int swapped;
      for (int i = 0; i < n - 1; i++) {
          swapped = 0;  // 标志位，初始化为未交换
          for (int j = 0; j < n - 1 - i; j++) {
              if (arr[j] > arr[j + 1]) {
                  // 交换相邻元素
                  int temp = arr[j];
                  arr[j] = arr[j + 1];
                  arr[j + 1] = temp;
                  swapped = 1;  // 发生交换，置标志位
              }
          }
          // 若一趟排序未发生任何交换，说明已完全有序
          if (swapped == 0) {
              break;
          }
      }
  }

6.4 快速排序

• 快速排序是对冒泡排序的一种改进，是一种不稳定的排序方法；

• 基本思想：通过一趟排序将要排序的数据分成独立的两个部分，其中一部分的所有数据都比另外一部分的所有数据要小，然后再分别对这两个部分进行快速排序，整个排序过程可以递归进行，从而使整个序列有序；

• 排序步骤

  • 在待排元素中任选一数据元素，以该元素为基准，将待排元素分为两部分，一部分小于该元素，一部分大于该元素；
  • 采用相同的方法对上一步的两部分分别进行快速排序；

• 时间复杂度

  • 平均情况：O(nlog⁡2n)O(n\log_{2}n)O(nlog2n)；

  • 最坏情况：即初始序列按关键字有序或基本有序时，快速排序的时间复杂度为O(n2)O(n^{2})O(n2)；

• 空间复杂度：需要栈空间来实现递归，栈空间最大深度为log⁡2n+1\log_{2}n + 1log2n+1，则空间复杂度为O(log⁡2n)O(\log_{2}n)O(log2n)；

• 例：将序列49、38、65、97、76、13、27从小到大排序

  • 第1趟快排（基准取第一个元素，pivot = 49，即经过第一趟快排后，要使得左边的数都<49，右边的数都＞49）：

    从 low 开始向右边找第一个大于 pivot 的元素，若找到则和 high 位置交换，即要将小的数放到 low 同时 high 指针左移一位；

    从 high 开始向左找第一个小于 pivot 的元素，若找到则和 low 位置交换，同时 low 指针右移一位；

    重复直到 low == high，最后把基准放到这个位置；

    通俗理解：

    • 要将小的数放到low这一边，要将大的数放到high这一边；
    • 交换到哪一边，哪一边就要移动指针。即小的数被放到low这一边，low就要移动指针。大的数被放到high这一边，high就要移动指针；
    • 可以通过此视频来辅助理解 high 和 low 指针的移动方式：https://v.douyin.com/wGLT0VMe9Q8/；

    • 初始时，low = 0（指向49），high = 6（指向27）；

      地址	0	1	2	3	4	5	6
      数据	49	38	65	97	76	13	27
      	low						high

    • 比较low = 0（指向49）和high = 6（指向27）所指向的值，49 > 27，将二者指向的值交换。low右移一位（low = 1），继续找比49大的元素；

      地址	0	1	2	3	4	5	6
      数据	27	38	65	97	76	13	49
      		low					high

    • 比较low = 1（指向38）和high = 6（指向49）所指向的值，38 < 49，小于49的数在49的左边，符合排序规则，不交换。low右移一位（low = 2），继续找比49大的元素；

      地址	0	1	2	3	4	5	6
      数据	27	38	65	97	76	13	49
      			low				high

    • 比较low = 2（指向65）和high = 6（指向49）所指向的值，65 > 49，将二者指向的值交换。high左移一位（high = 5），继续找比49小的元素；

      地址	0	1	2	3	4	5	6
      数据	27	38	49	97	76	13	65
      			low			high

    • 比较low = 2（指向49）和high = 5（指向13）所指向的值，49 > 13，将二者指向的值交换。low右移一位（low = 3），继续找比49大的元素；

      地址	0	1	2	3	4	5	6
      数据	27	38	13	97	76	49	65
      				low		high

    • 比较low = 3（指向97）和high = 5（指向49）所指向的值，97 > 49，将二者指向的值交换。high左移一位（high = 4），继续找比49小的元素；

      地址	0	1	2	3	4	5	6
      数据	27	38	13	49	76	97	65
      				low	high

    • 比较low = 3（指向49）和high = 4（指向76）所指向的值，49 < 76，大于49的数在49的右边，符合排序规则，不交换。high左移一位（high= 3），继续找比49小的元素；

      地址	0	1	2	3	4	5	6
      数据	27	38	13	49	76	97	65
      				low high

    • low = high = 3，第一趟快排结束。此时49的左边都是小于49的数，49的右边都是大于49的数；

  • 第2趟快排（对基准49左边的子序列27、38、13进行快速排序，基准取第一个元素，pivot = 27）：

  • 第3趟快排（对基准49右边的子序列76、97、65进行快速排序，基准取第一个元素，pivot = 76）：

• 代码：

  #include <iostream>
  using namespace std;
  const int N = 1e6 + 10;
  
  int n;
  int q[N];
  
  void quick_sort(int q[], int l, int r) {
  	// 当左指针大于等于右指针时，就直接退出
  	if (l >= r) return;
  	// 以最左边的数为分界点，i和j指针的初值分别指向数组的左右边界之外
  	int x = q[l], i = l - 1, j = r + 1;
  	while (i < j) {
  		// 先让i指针往中间方向移动一个位置，当i指针所指向的元素小于分界点时，就循环执行i++
  		do i++; while (q[i] < x);
  		// 先让j指针往中间方向移动一个位置，当j指针所指向的元素大于分界点时，就循环执行j++
  		do j--; while (q[j] > x);
  		// 当i指针和j指针都停止，且i指针还在j指针左边时，交换两个指针指向的元素
  		if (i < j) swap(q[i], q[j]);
  	}
  	// 先递归的排序左区间
  	quick_sort(q, l, j);
  	// 再递归的排序右区间
  	quick_sort(q, j + 1, r);
  }
  
  int main() {
  	scanf("%d", &n);
  	for (int i = 0; i < n; i++) scanf("%d", &q[i]);
  
  	// 传入q数组，和数组的左右边界索引
  	quick_sort(q, 0, n - 1);
  
  	for (int i = 0; i < n; i++) printf("%d ", q[i]);
  
  	return 0;
  }

6.5 简单选择排序

• 简单选择排序属于选择排序的一种，其基本思想是：从待排元素里选出最小的元素，把它放在已排序序列的末尾（通过和末尾后的第一个元素交换位置来实现），不断重复这个过程。并且，它是一种不稳定的排序方法；

• 时间复杂度 ：为 O(n2)O(n^2)O(n2)。这是因为在排序过程中，需要进行两层循环操作，外层循环控制排序的趟数，大约 nnn 次；内层循环用于在每一趟中寻找最小元素，大约 nnn 次，所以总的操作次数是 n×nn\times nn×n 量级，时间复杂度为 O(n2)O(n^2)O(n2)。

• 空间复杂度 ：仅需要一个元素的辅助空间来进行元素交换等操作，所以空间复杂度为 O(1)O(1)O(1)；

• 例：将序列49、38、65、97、76、13、27从小到大排序

  • 第1趟排序

    • 初始数据为：地址0到6对应的数据依次是49、38、65、97、76、13、27。要选择最小的元素放在位置0；

    • 首先，i 指向要将最小的元素放置的位置（初始默认是位置0），min 指向当前最小的元素（初始默认是49），j 指向指向（初始默认是位置1）；

      地址	0	1	2	3	4	5	6
      数据	49	38	65	97	76	13	27
      	min i	j

    • 将 j 指向的元素的值与 min 指向的元素的值比较，发现 38 < 49，则将 min 指向 38，同时 j 后移一位；

      地址	0	1	2	3	4	5	6
      数据	49	38	65	97	76	13	27
      	i	min	j

    • 将 j 指向的元素的值与 min 指向的元素的值比较，发现 65 > 38，min 指针不动，同时 j 后移一位；

      地址	0	1	2	3	4	5	6
      数据	49	38	65	97	76	13	27
      	i	min		j

    • 将 j 指向的元素的值与 min 指向的元素的值比较，发现 97 > 38，min 指针不动，同时 j 后移一位；

      地址	0	1	2	3	4	5	6
      数据	49	38	65	97	76	13	27
      	i	min			j

    • 将 j 指向的元素的值与 min 指向的元素的值比较，发现 76 > 38，min 指针不动，同时 j 后移一位；

      地址	0	1	2	3	4	5	6
      数据	49	38	65	97	76	13	27
      	i	min				j

    • 将 j 指向的元素的值与 min 指向的元素的值比较，发现 13 < 38，则将 min 指向 13，同时 j 后移一位；

      地址	0	1	2	3	4	5	6
      数据	49	38	65	97	76	13	27
      	i					min	j

    • 将 j 指向的元素的值与 min 指向的元素的值比较，发现 27 > 13，min 指针不动，同时 j 后移一位。此时 j 已经超出数组范围，第一趟排序结束；

      • 将 min 的值与 i 的值交换；
      • i 指向下一个要将最小的元素放置的位置（位置1）；
      • min 和 i 指向同一个位置（位置1）；
      • j 指向 i 的下一个位置（位置2）

      地址	0	1	2	3	4	5	6
      数据	13	38	65	97	76	49	27
      		i min	j

  • 第2趟排序

    • 现在数据变为：地址0到6对应的数据依次是13、38、65、97、76、49、27。接下来要选择最小的元素放在位置1；

      地址	0	1	2	3	4	5	6
      数据	13	38	65	97	76	49	27
      		i min	j

    • ......

6.6 堆排序

• 堆排序是选择排序的一种。堆是特殊的完全二叉树，堆顶元素（根结点）是堆中的最大值（大根堆）或最小值（小根堆），且任何一颗子树也都是堆；

  完全二叉树：一棵深度为 kkk、有 nnn 个节点的二叉树，按从上至下、从左到右 的顺序对节点编号。若编号为 i(1 \\leq i \\leq n) 的节点，与满二叉树中编号为 iii 的节点在二叉树中的位置相同，这棵二叉树就是完全二叉树；

• 基本思想

  • 将待排元素建立一个初始堆；

  • 输出堆顶的元素，即最大值（大根堆）或最小值（小根堆）；

  • 将剩余待排元素重新建立一个新的堆，重复上述步骤，直到所有元素排序完成；

• 建立初始堆的步骤

  • 对待排元素按层次遍历，构建一棵完全二叉树；

  • 从最后一个非叶子节点开始，按照堆的定义进行调整，使得父节点的值满足大根堆（父节点值大于子节点值）或小根堆（父节点值小于子节点值）的要求；

• 时间复杂度 ：O(nlog⁡2n)O(n\log_2 n)O(nlog2n)。建堆过程的时间复杂度为 O(n)O(n)O(n)，每次调整堆的时间复杂度为 O(log⁡2n)O(\log_2 n)O(log2n)，总共需要 nnn 次调整，所以总体时间复杂度为 O(nlog⁡2n)O(n\log_2 n)O(nlog2n)；

• 空间复杂度 ：仅需要一个元素的辅助空间用于元素交换等操作，空间复杂度为 O(1)O(1)O(1)；

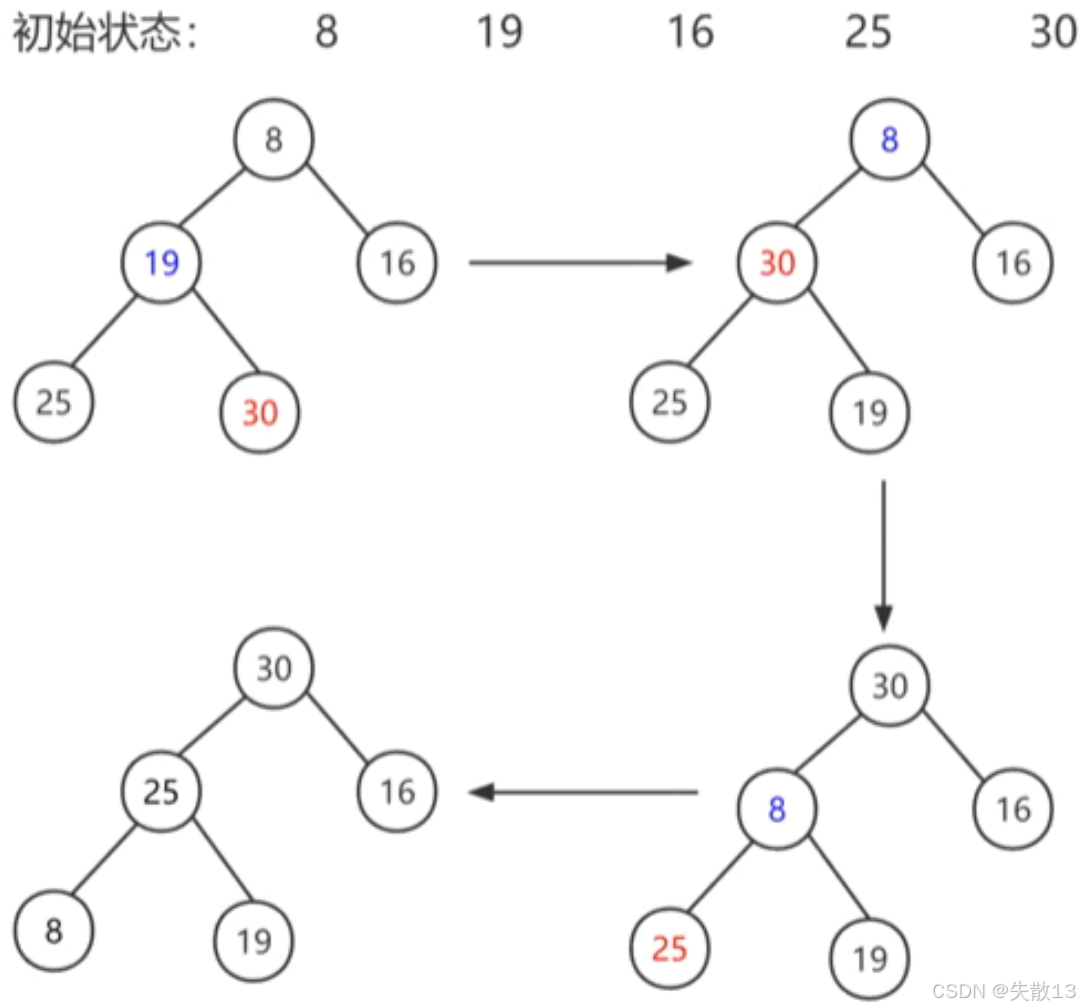
• 例：将序列8、19、16、25、30构建成大根堆

  • 首先按层次遍历构建完全二叉树（左上角图）
  • 从最后一个非叶子节点（值为19的节点）开始调整。比较19与其子节点25和30，30是最大的，所以19和30交换位置（右上角图）；
  • 接着调整根节点8，比较8与其子节点30和16，30最大，8和30交换位置（右下角图）；
  • 以8为根节点的子树此时不是大根堆，所以再次调整，8和25交换位置（左下角图）；

  

6.7 归并排序

• 归并排序的基本思想是将两个有序序列合并为一个有序序列，它采用分治法的策略，并且是一种稳定的排序方法；

• 时间复杂度 ：为 O(nlog⁡2n)O(n\log_2 n)O(nlog2n)。因为归并排序需要不断将序列分成两半，然后再合并，分的过程时间复杂度是 O(log⁡2n)O(\log_2 n)O(log2n)，合并的过程时间复杂度是 O(n)O(n)O(n)，所以总的时间复杂度是 O(nlog⁡2n)O(n\log_2 n)O(nlog2n)；

• 空间复杂度 ：需要 nnn 个元素的辅助空间来存储合并后的序列，所以空间复杂度为 O(n)O(n)O(n)；

• 例：初始序列为6、8、7、9、0、1、3、2、4、5

  • 分组与初步合并

    • 首先将序列两两分组，得到[6,8][6,8][6,8]、[7,9][7,9][7,9]、[0,1][0,1][0,1]、[3,2][3,2][3,2]、[4,5][4,5][4,5]这几个小组；

      6 8 7 9 0 1 3 2 4 5

    • 对每个小组内部进行排序合并，因为每个小组只有两个元素，比较后即可得到有序的小组：[6,8][6,8][6,8]（6和8已有序）、[7,9][7,9][7,9]（7和9已有序）、[0,1][0,1][0,1]（0和1已有序）、[2,3][2,3][2,3]（3和2比较后交换得到）、[4,5][4,5][4,5]（4和5已有序）；

      6   8   7  9   0  1   3    2  4   5
      \  /    \  /   \  /    \  /   \  /
       68      79     01     23      45

  • 进一步合并：接着将这些长度为2的有序子序列两两合并；

    • 6,8\]\[6,8\]\[6,8\]和\[7,9\]\[7,9\]\[7,9\]合并，比较6与7，6小先放入。然后8与7比较，7小放入。接着8与9比较，8小放入，最后放入9，得到\[6,7,8,9\]\[6,7,8,9\]\[6,7,8,9\]；

    • 4,5\]\[4,5\]\[4,5\]暂时等待后续合并； 6 8 7 9 0 1 3 2 4 5 \ / \ / \ / \ / \ / 68 79 01 23 45 \ / \ / | 6789 0123 45

    • 然后将[6,7,8,9][6,7,8,9][6,7,8,9]和[0,1,2,3][0,1,2,3][0,1,2,3]合并，从两个子序列的第一个元素开始比较，0最小先放入临时数组，接着1、2、3、6、7、8、9依次放入，得到[0,1,2,3,6,7,8,9][0,1,2,3,6,7,8,9][0,1,2,3,6,7,8,9]；

      6   8   7  9   0  1   3    2  4   5
      \  /    \  /   \  /    \  /   \  /
       68      79     01     23      45
        \      /       \     /       |
          6789          0123         45
           \             /           |
               01236789              45

    • 最后将这个长度为8的有序序列与[4,5][4,5][4,5]合并，4和5比前面序列的前几个元素大，所以在合适的位置插入，最终得到完全有序的序列[0,1,2,3,4,5,6,7,8,9][0,1,2,3,4,5,6,7,8,9][0,1,2,3,4,5,6,7,8,9]；

      6   8   7   9   0   1   3   2   4   5
      \  /    \  /    \  /    \  /    \  /
      68      79      01      23      45
       \      /         \      /        |
        6789             0123           45
           \            /               /
            \          /               /
             \        /               /
              \______/               /
                   01236789         /
                        \          /
                         \________/
                         0123456789

6.8 基数排序

• 基数排序的基本思想是按组成关键字的各个数位的值进行排序，它属于分配排序的一种，并且是一种稳定的排序方法；

• 时间复杂度 ：为 O(d(n+r))O(d(n + r))O(d(n+r))，其中 nnn 是待排元素的个数，ddd 是关键字的位数，rrr 是进制基数（比如十进制中 r=10r = 10r=10）。这是因为需要对每个数位进行排序，每个数位的排序操作涉及 nnn 个元素的分配等操作，共 ddd 个数位，所以时间复杂度与 ddd、nnn、rrr 相关；

• 空间复杂度 ：为 O(rd)O(rd)O(rd)，需要额外的空间来存储各个数位排序过程中的中间数据等；

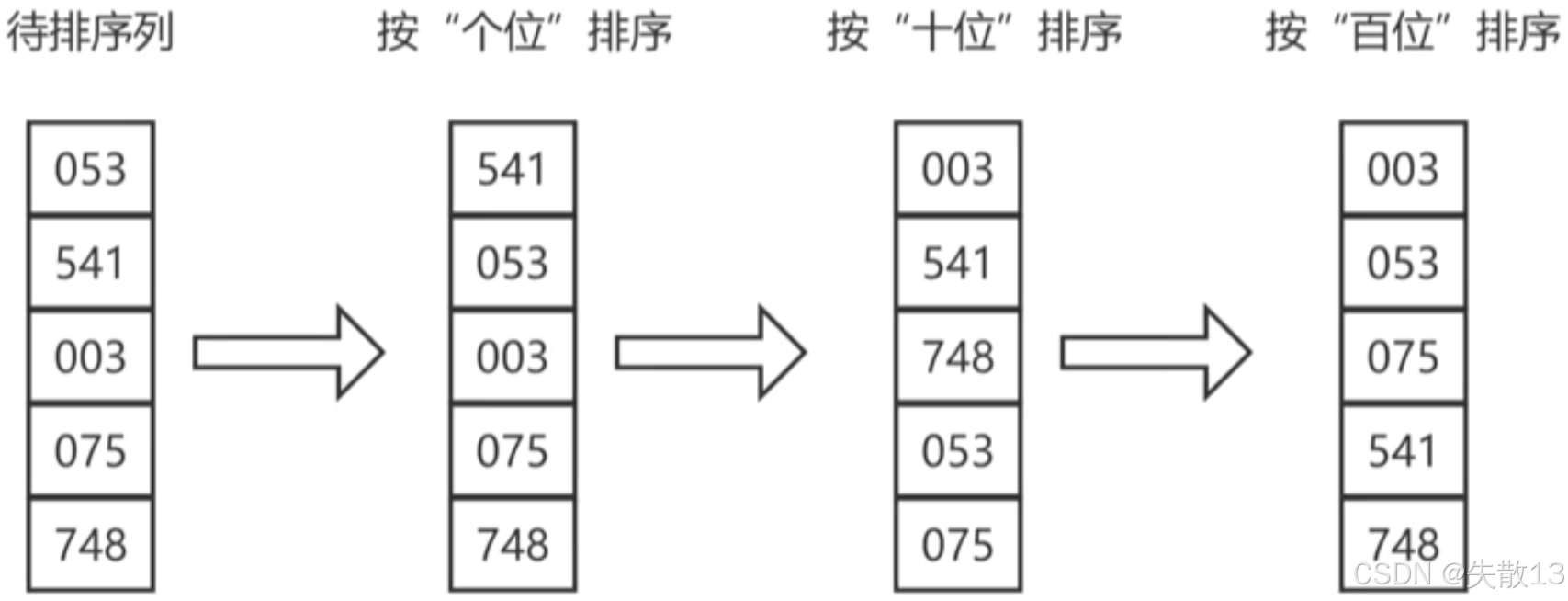
• 例：待排序列为053、541、003、075、748

  • 按"个位"排序：取出每个数的个位数字，分别是3（053）、1（541）、3（003）、5（075）、8（748）。根据个位数字的大小对原数进行排序，得到541（个位1）、053（个位3）、003（个位3）、075（个位5）、748（个位8）；

  • 按"十位"排序：在按个位排序后的序列基础上，取出每个数的十位数字，分别是4（541）、5（053）、0（003）、7（075）、4（748）。根据十位数字的大小对序列进行排序，得到003（十位0）、541（十位4）、748（十位4）、053（十位5）、075（十位7）；

  • 按"百位"排序：在按十位排序后的序列基础上，取出每个数的百位数字，分别是0（003）、0（541）、0（748）、0（053）、0（075）。因为百位数字都为0，所以序列顺序保持按十位排序后的结果，最终得到有序序列003、053、075、541、748；

  

6.9 小结

排序方法	时间复杂度	空间复杂度	稳定性
直接插入排序	O(n2)O(n^2)O(n2)	O(1)O(1)O(1)	稳定
简单选择排序	O(n2)O(n^2)O(n2)	O(1)O(1)O(1)	不稳定
冒泡排序	O(n2)O(n^2)O(n2)	O(1)O(1)O(1)	稳定
希尔排序	O(n1.3)O(n^{1.3})O(n1.3)	O(1)O(1)O(1)	不稳定
快速排序	O(nlog⁡2n)O(n\log_2 n)O(nlog2n)	O(log⁡2n)O(\log_2 n)O(log2n)	不稳定
堆排序	O(nlog⁡2n)O(n\log_2 n)O(nlog2n)	O(1)O(1)O(1)	不稳定
归并排序	O(nlog⁡2n)O(n\log_2 n)O(nlog2n)	O(n)O(n)O(n)	稳定
基数排序	O(d(n+r))O(d(n + r))O(d(n+r))	O(rd)O(rd)O(rd)	稳定