目录
算法能解决的问题
- 动态单点/区间属性修改
- 动态区间查询
算法原理
将一个大的区间递归地分解成若干个不相交的小区间 , 并且在分解 过程中预先计算出区间的初始信息, 具体的来说, 线段树一般有如下操作
push up(x)用子节点信息 计算父节点信息, 也就是自下而上的push down(x)用父节点信息 更新子节点信息 , 是自上而下 的, 也就是延迟标记build(l, r)将一段区间初始化成线段树modify(u, x, val)修改单点modify(u, l, r, val)修改区间 一般需要延迟标记, 情况较为复杂query(l, r)查询某一段区间的信息
线段树的存储
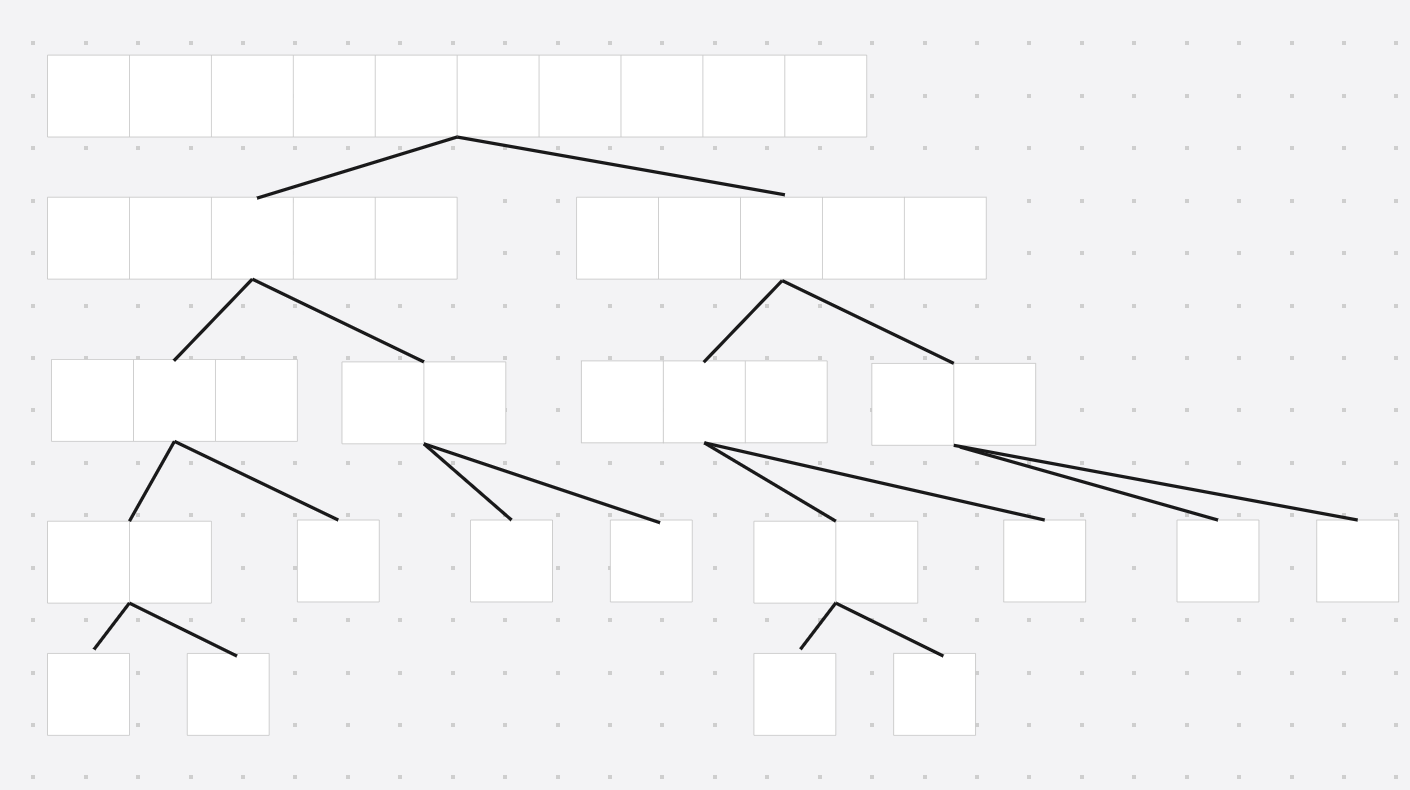
除了最后一层, 剩余情况都是满二叉树 , 因此可以使用堆的形式 存储线段树
对于当前节点 u u u, 它的左子节点是u << 1, 右子节点是u << 1 | 1
线段树点的数量以及空间大小
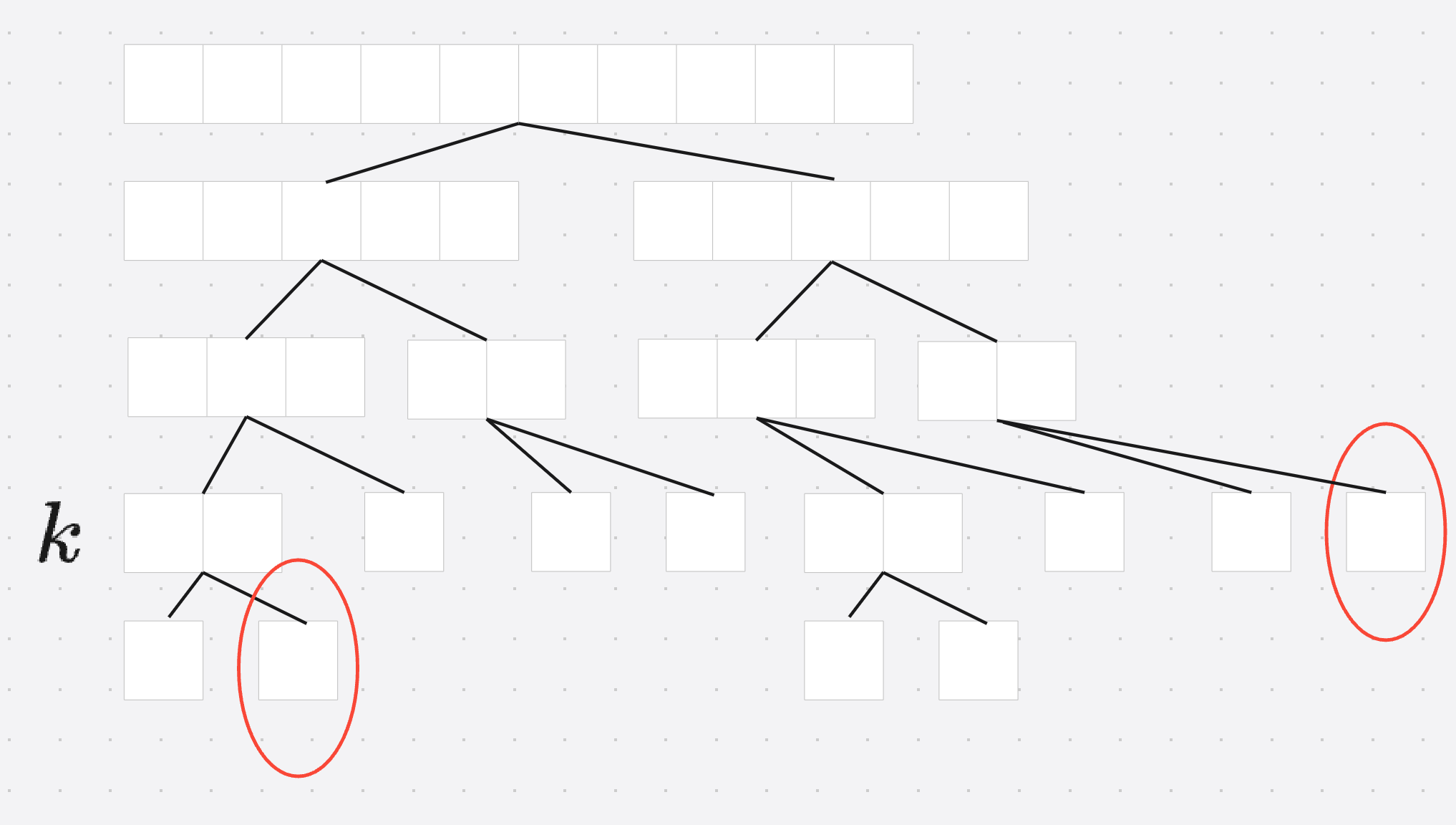
假设预处理的是 1 ∼ n 1 \sim n 1∼n之间的区间, 线段树的单独的子节点(类似于上图红色框住的点)的数量一定是 n n n个, 因此 倒数第二层节点数量 ≤ n \le n ≤n
因为前面的都是满二叉树, 节点总数等于
2 0 + 2 1 + 2 2 + . . . + 2 k − 1 = 2 k − 1 2 ^ 0 + 2 ^ 1 + 2 ^ 2 + ... + 2 ^ {k - 1} = 2 ^ k - 1 20+21+22+...+2k−1=2k−1
当前层节点数是 2 k ≤ n 2 ^ k \le n 2k≤n, 因此算上倒数第二层节点总数 ≤ 2 n − 1 \le 2n - 1 ≤2n−1
因为最后一层可能达到满二叉树的情况也就是 ≤ 2 n \le 2n ≤2n , 因此总的节点数量
s ≤ 2 n + 2 n − 1 = 4 n − 1 s \le 2n + 2n - 1 = 4n - 1 s≤2n+2n−1=4n−1
因此在给线段树 分配空间的时候, 一般倾向于分配 4 4 4倍空间!
延迟标记的线段树
为什么区间修改线段树需要延迟标记 ?

假设修改的是这样一颗线段树, 修改一段区间最坏情况下节点个数是 4 ∗ n 4 * n 4∗n个, 时间复杂度是 O ( 4 n ) O(4n) O(4n), 效率很低
因此需要增加一些信息和操作使得修改区间的时间复杂度降低 , 以区间新增一个数字为例 , 题面在进阶数据结构应用-一个简单的整数问题2(Fenwick-Tree 解法)
设计线段树节点
cpp
struct Node {
int l, r;
LL sum, add;
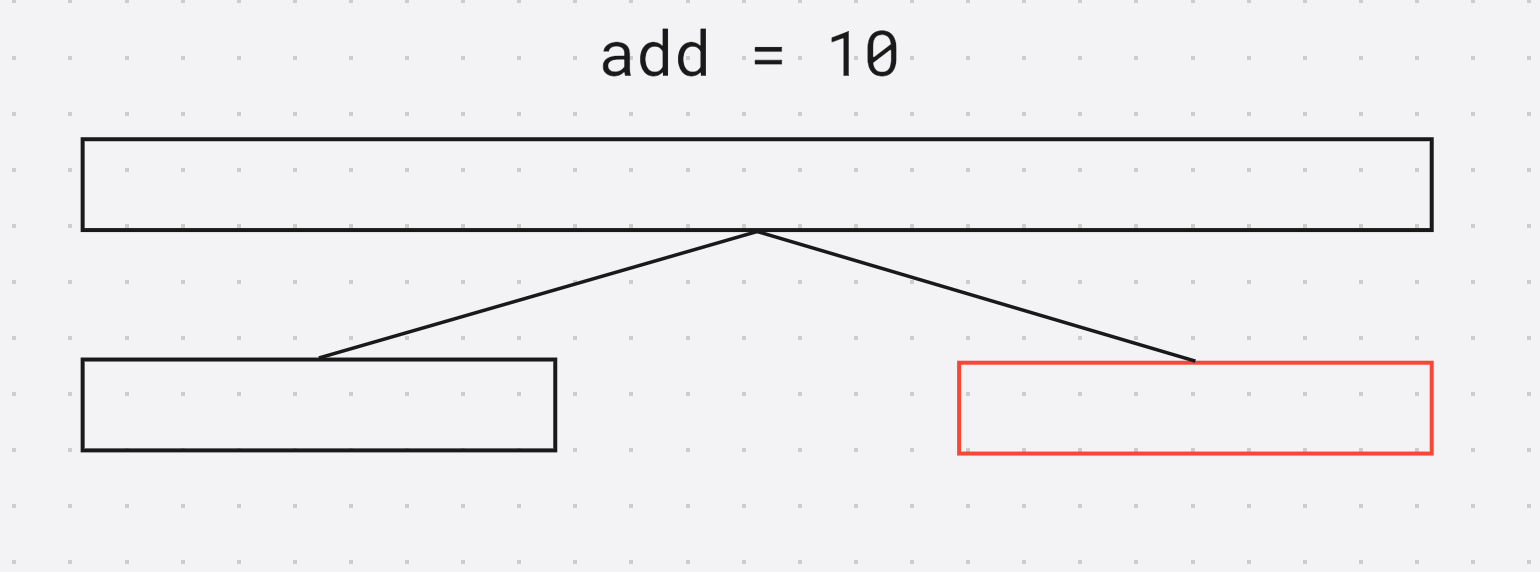
};add就是延迟标记, 含义是以当前节点为根节点的子树中的每一个节点都要加上add (不包含根节点)
当前节点的标记未向下传播, 只给根节点打上了标记, 直接返回
这样操作的算法时间复杂度 O ( log n ) O(\log n) O(logn)
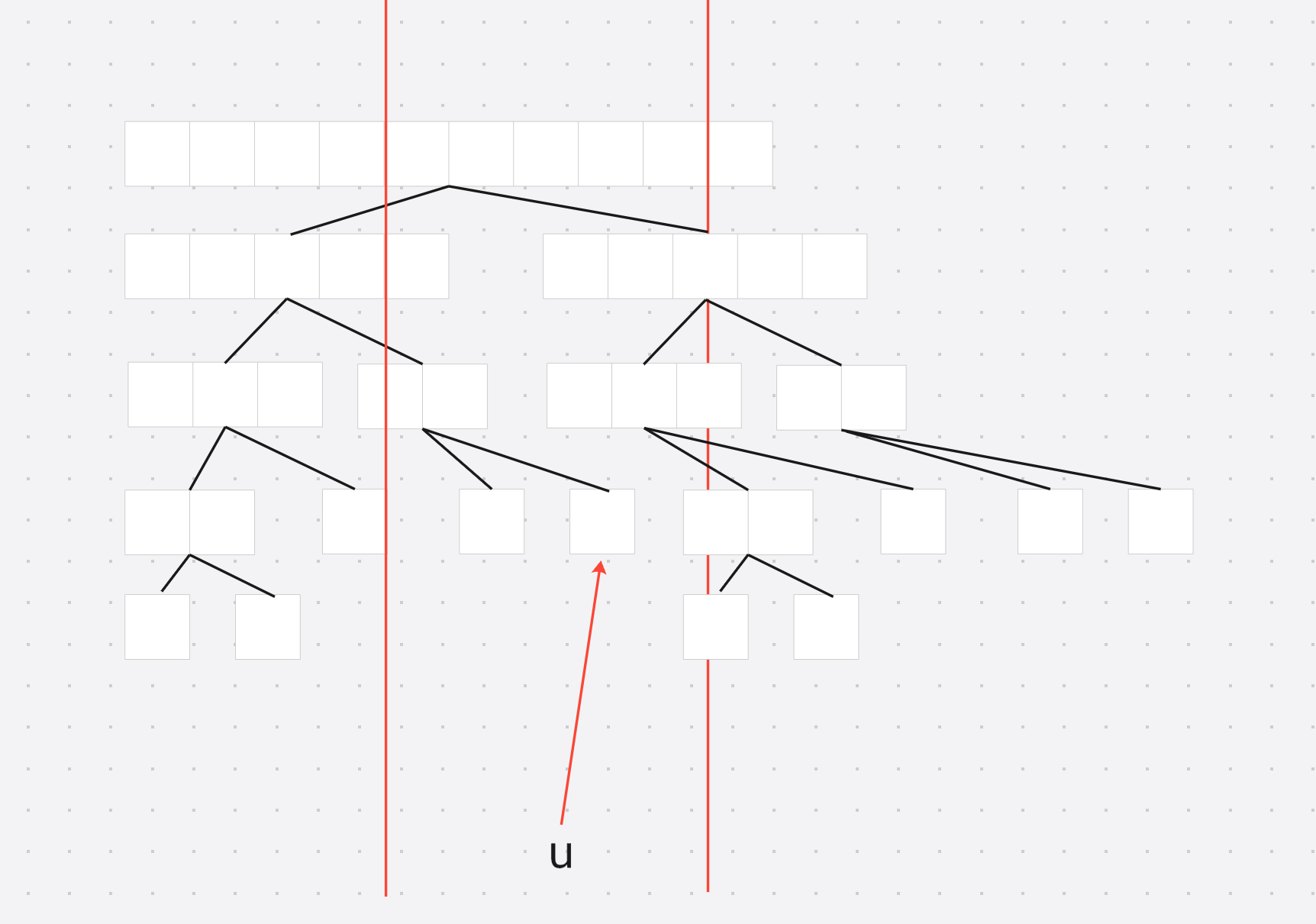
假设计算红色区间内的区间和, 对于当前节点 u u u, 在计算的时候需要累计父节点所有的延迟标记 , 也就是需要延迟标记下传 , 因此在查询过程中 需要将当前位置的所有祖先节点的延迟标记的值 累加到当前节点上
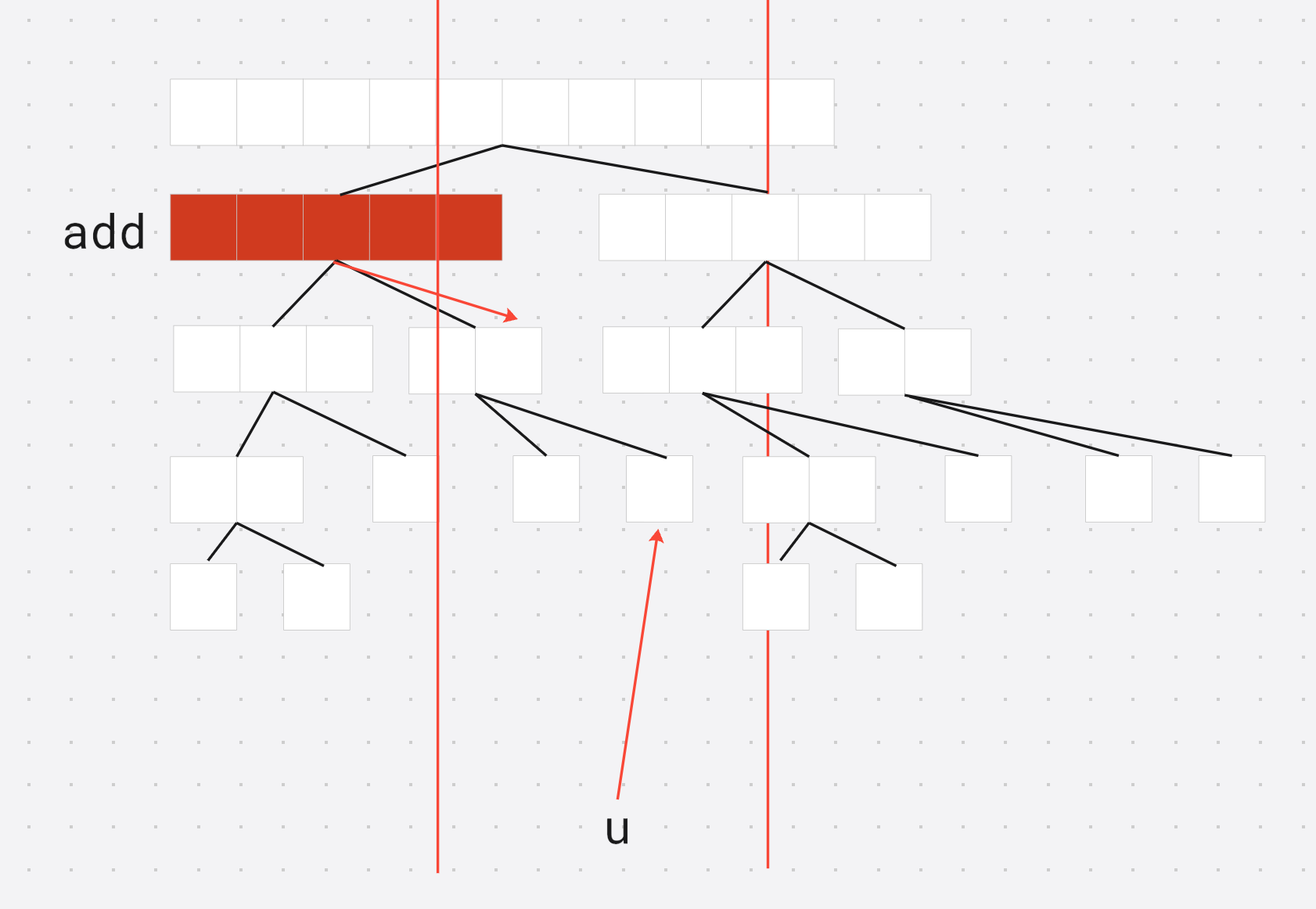
在查询过程中, 发现当前红色区间覆盖范围太大 , 需要向下递归到子区间, 做如下操作
- 将延迟标记下传到子节点
- 将延迟标记清空
具体的来说, 伪代码如下
cpp
struct Node {
int l, r;
LL sum, add;
};
void pushdown(Node &u, Node &ls, Node &rs) {
ls.add += u.add, rs.add += u.add;
ls.sum += (ls.r - ls.l + 1) * u.add;
rs.sum += (rs.r - rs.l + 1) * u.add;
u.add = 0;
}
在修改的时候, 也需要将当前延迟标记向下传, 例如假设当前区间的延迟标记是 + 10 +10 +10, 但是目标是将右子区间再加 20 20 20 , 分为两步
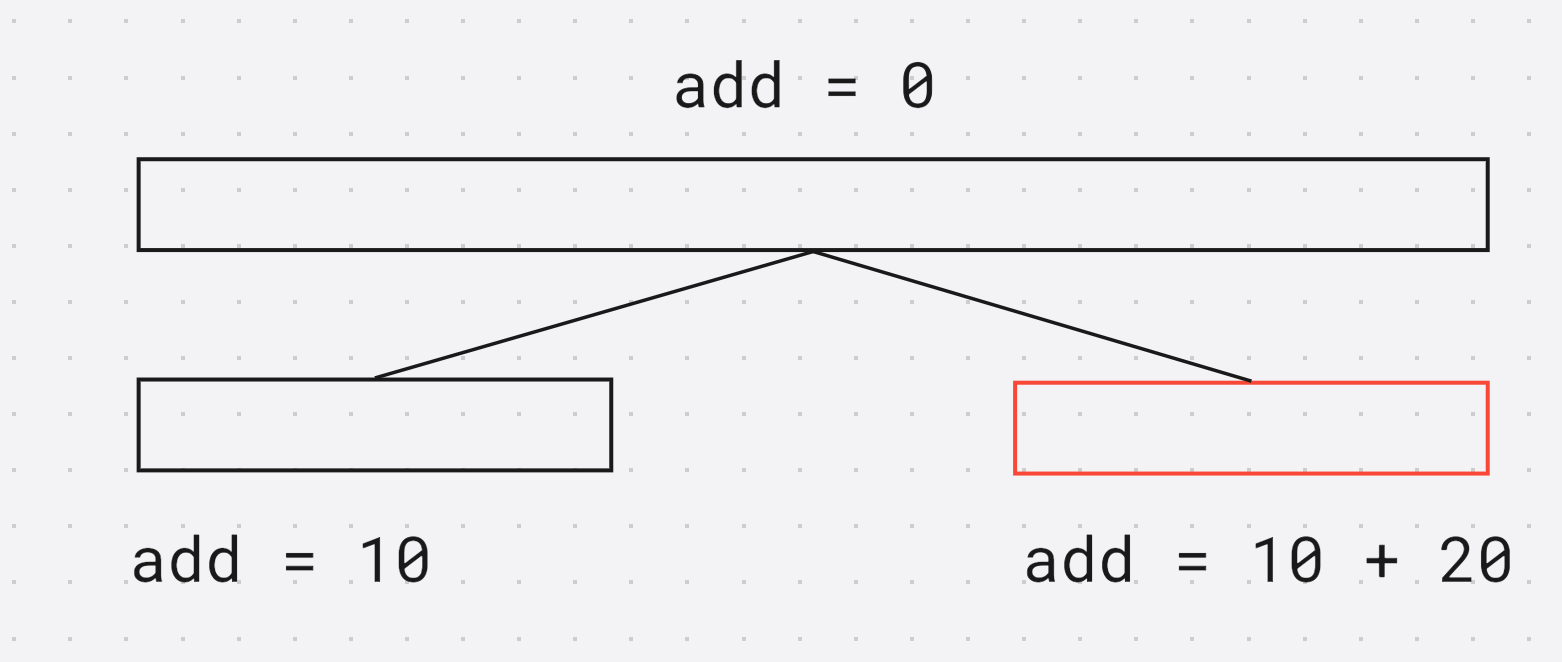
- 先将延迟标记下传
- 再将子区间的延迟标记 加上 20 20 20
线段树扫描线
进阶数据结构应用-线段树扫描线
算法步骤
- 确定线段树中需要存储什么属性
- 观察是否是区间修改 问题, 如果是需要开延迟标记
- 线段树建立 4 4 4倍空间
- 实现
push up和push down操作, 在递归调用前push down, 在递归调用后push up - 实现查询和修改操作