《信息学奥赛一本通》第148题:求三角形面积
题目背景
本题虽然作为《信息学奥赛一本通》第二章的习题,但是会用到第三章的知识点。
题目描述
编写一个程序,给定三条线段的长度 a , b , c a,b,c a,b,c,判断这三条线段是否能够构成三角形。如果能够构成,则计算其面积。如果不能构成,输出
No solution.(注意句号)。输入格式
输入只有一行,包含三个正实数 a , b , c a,b,c a,b,c,小数点后最多只有一位,且每个数均不超过 100 100 100。
输出格式
输出只有一行,如果能构成三角形,输出三角形的面积(保留两位小数),否则输出
No solution.。输入输出样例 #1
输入 #1
3 4 5
输出 #1
6.00
说明/提示
海伦公式: 若三角形的边长为 a , b , c a, b, c a,b,c,则三角形的面积是 s ( s − a ) ( s − b ) ( s − c ) \sqrt{s(s-a)(s-b)(s-c)} s(s−a)(s−b)(s−c) ,其中 s = 1 2 ( a + b + c ) s=\frac{1}{2}(a+b+c) s=21(a+b+c)。
大家好,我是莫小特。
这篇文章给大家带来《信息学奥赛一本通》中的第 148 题:求三角形面积。

一、题目描述
洛谷的题号是:B2149 求三角形面积
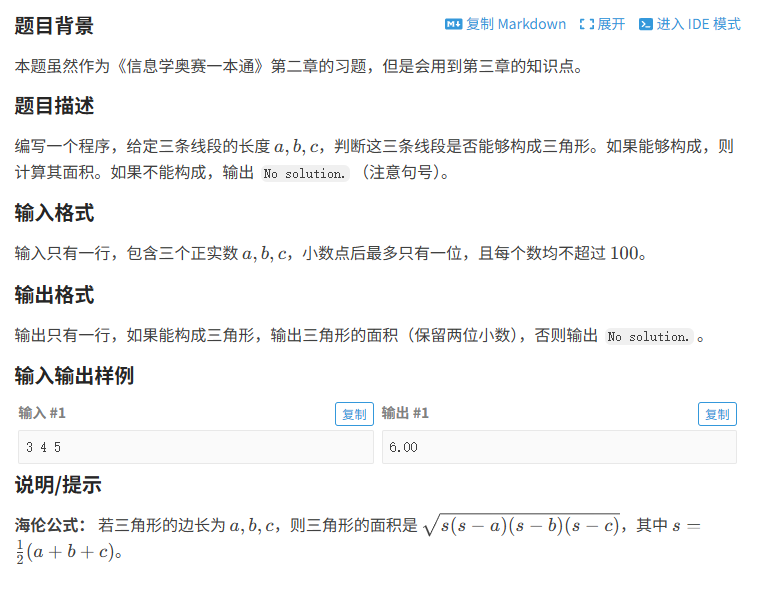
二、题意分析
这道题是信息学奥赛一本通练习题的第 148 题。
根据输入格式的描述,输入只有一行,包含三个正实数 a、b、c,小数点最多只有一位,且每个数均不超过 100,所以使用 double 类型。
cpp
double a,b,c;
cin>>a>>b>>c;根据题目意思,要先判断这三个线段是否能构成三角形,如果能构成,则计算面积,如果不能构成,就输出 No solution.,所以先判断这三个线段是否能构成三角形。
直角三角形的特点是:两边之和大于第三边,所以需要做判断。
cpp
if(a+b>c&&b+c>a&&a+c>b)
{
}
else
{
cout<<"No solution.";
}接下来在 if 语句中添加计算三角形面积的代码,根据海伦公式: s ( s − a ) ( s − b ) ( s − c ) \sqrt{s(s-a)(s-b)(s-c)} s(s−a)(s−b)(s−c) ,所以需要变量来计算 s,定义一个 double 类型变量 s,存储 s = 1 2 ( a + b + c ) s=\frac{1}{2}(a+b+c) s=21(a+b+c)。
cpp
double s=0.5*(a+b+c);面积的计算需要用到开平方,使用 sqrt 函数,加上 #include<cmath> 头文件,新建一个 double 类型变量存储面积。
cpp
#include<cmath>
double mj=sqrt(s*(s-a)*(s-b)*(s-c));输出三角形面积,保留两位小数,使用 printf 函数。
cpp
printf("%.2lf",mj);按照样例输入对数据进行验证。

符合样例输出,到网站提交测评。
测试通过!
三、完整代码
该题的完整代码如下:
cpp
#include<cmath>
#include<iostream>
#include<bits/stdc++.h>
using namespace std;
int main()
{
double a,b,c;
cin>>a>>b>>c;
if(a+b>c&&b+c>a&&a+c>b)
{
double s=0.5*(a+b+c);
double mj=sqrt(s*(s-a)*(s-b)*(s-c));
printf("%.2lf",mj);
}
else
{
cout<<"No solution.";
}
return 0;
}四、总结
本题考察了条件判断与海伦公式的应用,主要涵盖以下知识点:
1、三角形判定
(1)三角形成立条件:任意两边之和大于第三边。
(2)若不满足条件,直接输出 "No solution."。
2、公式应用
(1)利用海伦公式计算面积: s = 1 2 ( a + b + c ) s=\frac{1}{2}(a+b+c) s=21(a+b+c),面积 = s ( s − a ) ( s − b ) ( s − c ) =\sqrt{s(s-a)(s-b)(s-c)} =s(s−a)(s−b)(s−c) 。
(2)注意调用 sqrt 函数时需引入 <cmath> 头文件。
3、输出格式控制
结果需保留两位小数,可用 printf("%.2lf", ...) 或 cout<<fixed<<setprecision(2)。
常见易错点与解题建议:
1、三角形判定条件错误
有的同学会误写成"大于等于",导致退化成一条直线时也输出面积。
👉 建议:严格使用 >,避免边界错误。
2、公式中 s 计算错误
忘记除以 2 或者直接写成 (a+b+c)/3。
👉 建议:推导公式时先写草稿,确保公式正确。
3、开平方函数遗漏头文件
使用 sqrt 时忘记 #include <cmath>,编译报错。
👉 建议:涉及数学函数时检查头文件是否齐全。
4、输出格式不符合要求
若使用 cout 默认格式,可能输出多位或少位小数。
👉 建议:养成使用 printf 或 iomanip 控制精度的习惯。
---end---
如果你觉得这篇文章对你有帮助,欢迎点赞、收藏、关注我哦!
如果有更好的方法也可以在评论区评论哦,我都会看哒~
我们下集见~