考研数学：使用有理根定理和多项式除法来解一元多次整系数方程

在考研数学中，求解一元高次方程（通常指三次及以上）的实数根是一个常见考点。这类题目往往设计精巧，不会要求考生使用繁琐的求根公式，而是考查对有理根定理 和多项式除法的综合应用能力。掌握这套"组合拳"，能让你在考场上快速、准确地解决此类问题。

一、核心武器库：有理根定理

有理根定理为我们提供了寻找方程有理根（如果存在的话）的系统性方法。

定理内容：对于一个一元 n 次整系数多项式方程：

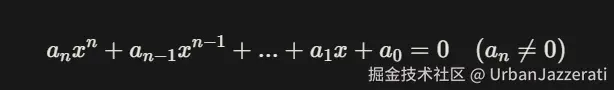
<math xmlns="http://www.w3.org/1998/Math/MathML"> 其任何可能的有理根 x = p q 必须满足：其任何可能的有理根x=\frac{p}{q}必须满足： </math>其任何可能的有理根x=qp必须满足：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> p 是常数项 a 0 的因数。 q 是最高次项系数 a n 的因数。 p是常数项 a_0 的因数。 q是最高次项系数 a_n 的因数。 </math>p是常数项a0的因数。q是最高次项系数an的因数。

操作步骤：

列出所有候选根 ：找出 <math xmlns="http://www.w3.org/1998/Math/MathML"> a 0 a_0 </math>a0 的所有正负因数（ <math xmlns="http://www.w3.org/1998/Math/MathML"> p p </math>p）和 <math xmlns="http://www.w3.org/1998/Math/MathML"> a n a_n </math>an 的所有正负因数（ <math xmlns="http://www.w3.org/1998/Math/MathML"> q q </math>q），然后列出所有可能的有理数 <math xmlns="http://www.w3.org/1998/Math/MathML"> p q \frac{p}{q} </math>qp（通常需约分为最简形式）。
代入验证（试根） ：将候选根逐个代入原方程，若满足 <math xmlns="http://www.w3.org/1998/Math/MathML"> f ( x ) = 0 ， f(x)=0， </math>f(x)=0，则该值即为方程的一个根。

考研应用提示 ：考研真题中的方程，其有理根通常是较小的整数，如 <math xmlns="http://www.w3.org/1998/Math/MathML"> ± 1 , ± 2 , ± 3 ±1,±2,±3 </math>±1,±2,±3优先尝试这些数值可以节省大量时间。

二、降维打击：多项式除法

当我们通过有理根定理找到一个根 <math xmlns="http://www.w3.org/1998/Math/MathML"> x = k x x=kx </math>x=kx后，就意味着多项式含有因式 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( x − k ) (x−k) </math>(x−k)。此时，我们需要使用多项式除法 （或综合除法）来降低方程的次数。

多项式除法（长除法） ：将原多项式 <math xmlns="http://www.w3.org/1998/Math/MathML"> f ( x ) f(x) </math>f(x) 除以因式 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( x − k ) (x−k) </math>(x−k)，得到一个商式 <math xmlns="http://www.w3.org/1998/Math/MathML"> g ( x ) g(x) </math>g(x)（次数比原式低一次）和一个余数。若 kkk 确实是根，则余数必为0。即有：

<math xmlns="http://www.w3.org/1998/Math/MathML"> f ( x ) = ( x − k ) ⋅ g ( x ) f(x)=(x−k)⋅g(x) </math>f(x)=(x−k)⋅g(x)

原方程 <math xmlns="http://www.w3.org/1998/Math/MathML"> f ( x ) = 0 就转化为 ( x − k ) ⋅ g ( x ) = 0 。 f(x)=0 就转化为 (x−k)⋅g(x)=0。 </math>f(x)=0就转化为(x−k)⋅g(x)=0。
综合除法（快速技巧） ：综合除法是多项式除法的简化版，更适合线性因式 (x−k)(x - k)(x−k)，计算更便捷，书写更简洁，是考场上强烈推荐的技巧。

三、实战四步法：解题流程

面对一道一元高次方程求解题，请遵循以下四步：

第一步：观察整理 将方程所有项移到等号一侧，按降幂排列，确保是标准形式 <math xmlns="http://www.w3.org/1998/Math/MathML"> f ( x ) = 0 。 f(x)=0。 </math>f(x)=0。

第二步：有理试根

列出所有可能的有理根候选。
优先尝试 ： <math xmlns="http://www.w3.org/1998/Math/MathML"> ± 1 , ± 2 ±1,±2 </math>±1,±2等简单整数。
找到一个根 <math xmlns="http://www.w3.org/1998/Math/MathML"> x = k x x=kx </math>x=kx。

第三步：降次分解 利用综合除法 ，用找到的根 <math xmlns="http://www.w3.org/1998/Math/MathML"> k k </math>k 对原多项式进行降次，得到商式 <math xmlns="http://www.w3.org/1998/Math/MathML"> g ( x ) g(x) </math>g(x)。即： <math xmlns="http://www.w3.org/1998/Math/MathML"> f ( x ) = ( x − k ) ⋅ g ( x ) f(x)=(x−k)⋅g(x) </math>f(x)=(x−k)⋅g(x)

第四步：求解余式 方程转化为：

<math xmlns="http://www.w3.org/1998/Math/MathML"> ( x − k ) ⋅ g ( x ) = 0 (x−k)⋅g(x)=0 </math>(x−k)⋅g(x)=0

解 <math xmlns="http://www.w3.org/1998/Math/MathML"> x − k = 0 ，得 x 1 = k 。 x−k=0，得 x_1=k。 </math>x−k=0，得x1=k。
解 <math xmlns="http://www.w3.org/1998/Math/MathML"> g ( x ) = 0 。如果 g ( x ) g(x)=0。如果 g(x) </math>g(x)=0。如果g(x) 是二次式，可直接用求根公式；若次数仍较高，则对 <math xmlns="http://www.w3.org/1998/Math/MathML"> g ( x ) g(x) </math>g(x) 重复第二步 和第三步，直至所有根都被求出。

四、真题演练

例题：求解方程 <math xmlns="http://www.w3.org/1998/Math/MathML"> f ( x ) = x 4 − 2 x 3 − 3 x 2 + 4 x + 4 = 0 f(x) = x^4 - 2x^3 - 3x^2 + 4x + 4 = 0 </math>f(x)=x4−2x3−3x2+4x+4=0

解：

试根：常数项为4，系数为1。可能有理根： <math xmlns="http://www.w3.org/1998/Math/MathML"> ± 1 , ± 2 , ± 4 。 ±1,±2,±4。 </math>±1,±2,±4。
- 试 <math xmlns="http://www.w3.org/1998/Math/MathML"> x = − 1 : f ( − 1 ) = 1 + 2 − 3 − 4 + 4 = 0 x=−1: f(−1)=1+2−3−4+4=0 </math>x=−1:f(−1)=1+2−3−4+4=0 ✅ 找到第一个根 <math xmlns="http://www.w3.org/1998/Math/MathML"> x 1 = − 1 x_1=−1 </math>x1=−1。

综合除法（降次） ：用 −1-1−1 对多项式进行综合除法。

lua 复制代码

系数: | 1   -2   -3    4    4
根 -1 |     -1    3    0    -4
      | --------------------------
      |  1  -3    0    4    0

商式为 <math xmlns="http://www.w3.org/1998/Math/MathML"> x 3 − 3 x 2 + 4 ，余数为 0 。 ∴ f ( x ) = ( x + 1 ) ( x 3 − 3 x 2 + 4 ) . x^3 - 3x^2 + 4，余数为0。 ∴ f(x) = (x + 1)(x^3 - 3x^2 + 4). </math>x3−3x2+4，余数为0。∴f(x)=(x+1)(x3−3x2+4).

对商式 <math xmlns="http://www.w3.org/1998/Math/MathML"> g ( x ) = x 3 − 3 x 2 + 4 g(x) = x^3 - 3x^2 + 4 </math>g(x)=x3−3x2+4重复过程。
- 试根： <math xmlns="http://www.w3.org/1998/Math/MathML"> 可能根 ± 1 , ± 2 , ± 4 可能根 ±1,±2,±4 </math>可能根±1,±2,±4。h
  - 试 <math xmlns="http://www.w3.org/1998/Math/MathML"> x = 2 : g ( 2 ) = 8 − 12 + 4 = 0 x=2: g(2)=8−12+4=0 </math>x=2:g(2)=8−12+4=0 ✅ 找到第二个根 <math xmlns="http://www.w3.org/1998/Math/MathML"> x 2 = 2 x_2 =2 </math>x2=2。
- 综合除法 ：用 2 对 <math xmlns="http://www.w3.org/1998/Math/MathML"> g ( x ) g(x) </math>g(x) 进行综合除法。
  lua 复制代码
```
系数：| 1   -3    0<-不要漏 4
根 2 |       2   -2   -4
     | --------------------
        1   -1   -2    0
```
  新的商式为 <math xmlns="http://www.w3.org/1998/Math/MathML"> x 2 − x − 2 x^2 - x - 2 </math>x2−x−2，余数为0。 <math xmlns="http://www.w3.org/1998/Math/MathML"> ∴ g ( x ) = ( x − 2 ) ( x 2 − x − 2 ) 综上： f ( x ) = ( x + 1 ) ( x − 2 ) ( x 2 − x − 2 ) ∴ g(x) = (x - 2)(x^2 - x - 2) 综上：f(x) = (x + 1)(x - 2)(x^2 - x - 2) </math>∴g(x)=(x−2)(x2−x−2)综上：f(x)=(x+1)(x−2)(x2−x−2)
解低次方程 ：分解 <math xmlns="http://www.w3.org/1998/Math/MathML"> x 2 − x − 2 = ( x − 2 ) ( x + 1 ) 。 ∴ f ( x ) = ( x + 1 ) 2 ( x − 2 ) 2 = 0 x^2 - x - 2 = (x - 2)(x + 1)。 ∴ f(x) = (x + 1)^2 (x - 2)^2 = 0 </math>x2−x−2=(x−2)(x+1)。∴f(x)=(x+1)2(x−2)2=0
最终解：

<math xmlns="http://www.w3.org/1998/Math/MathML"> ( x + 1 ) 2 = 0 或 ( x − 2 ) 2 = 0 (x + 1)^2 = 0 \quad \text{或} \quad (x - 2)^2 = 0 </math>(x+1)2=0或(x−2)2=0

得方程的解为： <math xmlns="http://www.w3.org/1998/Math/MathML"> x 1 = x 2 = − 1 , x 3 = x 4 = 2 （二重根）。 \boxed{x_1 = x_2 = -1,\quad x_3 = x_4 = 2}（二重根）。 </math>x1=x2=−1,x3=x4=2（二重根）。

五、总结与备考建议

核心思维：有理根定理是"探测器"，多项式除法是"拆解器"，二者结合，将高次方程拆解为我们会解的低次方程。
效率优先 ：在考场上，综合除法远比多项式长除法快捷，务必熟练掌握。
练习重点 ：多找考研真题中的类似题目进行练习，尤其注意方程有重根、根为分数等稍复杂的情况，做到熟能生巧。