目录
除自身外数组的乘积
解法:前缀和(积)
两个数组分别计算前缀积后各自进行相乘,因为多开了一个空间,所以是:
ans = left_sum[i]*right_sum[i+1]
cpp
class Solution
{
public:
vector<int> productExceptSelf(vector<int> &nums)
{
int n = nums.size();
vector<int> left_sum(n+1,1),right_sum(n+1,1);
//从左到右的前缀积
for(int i=0;i<n;i++)
{
left_sum[i+1]=left_sum[i]*nums[i];
}
//从右到左的前缀积
for(int i=n-1;i>=0;i--)
{
right_sum[i]=right_sum[i+1]*nums[i];
}
vector<int> ret;
for(int i=0;i<n;i++)
{
ret.push_back(left_sum[i]*right_sum[i+1]);
}
return ret;
}
};也可以不多开空间,先计算从右向左的前缀积后,使用变量边计算从左向右的前缀积,边更新出答案,空间复杂度为 O(1)
cpp
class Solution
{
public:
vector<int> productExceptSelf(vector<int> &nums)
{
int n = nums.size();
// 不需要多开一个空间也可以解决
vector<int> right_sum(n, 1);
// 从右到左的前缀积
for (int i = n - 2; i >= 0; i--)
{
right_sum[i] = right_sum[i + 1] * nums[i + 1];
}
int tmp = 1;
for (int i = 0; i < n; i++)
{
right_sum[i] = tmp * right_sum[i];
tmp *= nums[i];
}
return right_sum;
}
};加油站
解法1:暴力
遍历每个位置,看看是否能走到起点,但 O(N) = N^2,超时
解法2:规律
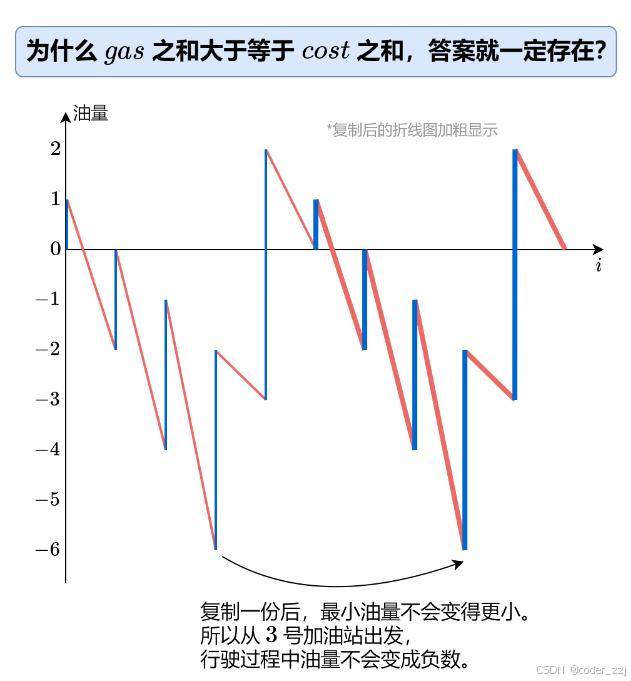
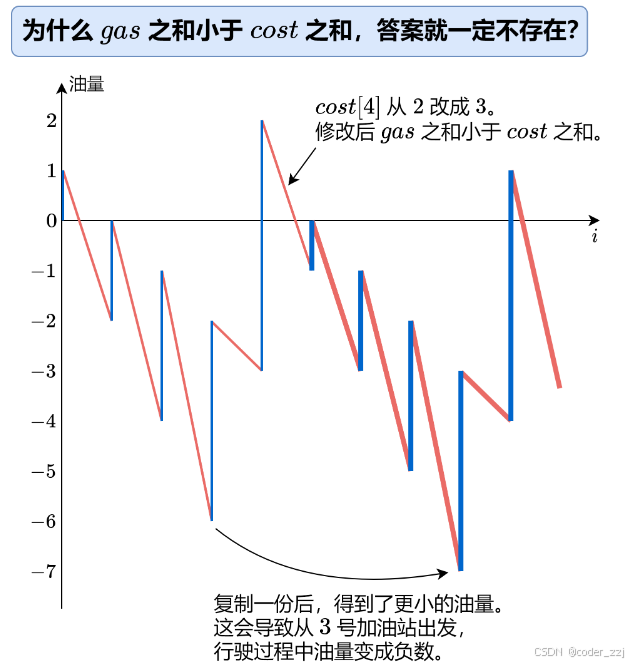
结论:总油量 > 耗油量 时,一定不能走到起点;反之则可以,但关键是要怎么快速找到该位置? 从0位置为起点模拟一遍(画成折线图),最低点则是答案,因为从最低点出发到原点,一定出现不会比最低点还低的情况
cpp
class Solution
{
public:
int canCompleteCircuit(vector<int> &gas, vector<int> &cost)
{
int n = gas.size(), sum = 0;
int ret = 0, tmp = INT_MAX;
for (int i = 0; i < n; i++)
{
sum += gas[i] - cost[i];
if (tmp > sum)
{
tmp = sum;
ret = i + 1; // 此时-cost[i]已经来到了i+1位置了
}
}
return sum < 0 ? -1 : ret % n; // 可能答案在0位置,但i+1越界了
}
};分发糖果
解法1:暴力
左右遍历一遍,取每个位置的最大值相加就是答案
解法2:分组循环
定义 sum = ratings.size(),表示孩子至少有一颗糖
- 每次循环时,先看看 ratings[i-1] < ratings[i],如果是的话就说明可以从 i-1 位置开始找,否则就从 i 位置开始,start = i-1 或者 i
- 循环找顶峰,当 ratings[i] >= ratings[i+1] 时就说明找到顶峰 top = i,同时形成也是等差数列,比如 0 1 2 3...使用等差数列和求出递增组的糖果数量(n = top - start)n*(n-1)/2(除去顶峰)
- 从顶峰开始找峰谷,当 ratings[i] <= ratings[i+1] 时就说明找到峰谷 end = i,同样使用等差数列和求糖果数量(n = end - top)n*(n-1)/2 (除去顶峰)
- 最后还要统计出峰谷的数量,也就是左右糖果的最大值,这才能保证评分更高的那个会获得更多的糖果
cpp
class Solution
{
public:
int candy(vector<int> &ratings)
{
int n = ratings.size(), i = 0;
int start, top, end, sum = n, tmp1, tmp2;
for (int i = 0; i < n; i++)
{
// 上组递减的最后一个数(谷底)会被共享
if (i - 1 >= 0 && ratings[i - 1] < ratings[i])
start = i - 1;
else
start = i;
while (i + 1 < n && ratings[i] < ratings[i + 1])
i++;
top = i;
tmp1 = top - start;
// 递增相加,刚好是等差数列
sum += tmp1 * (tmp1 - 1) / 2;
while (i + 1 < n && ratings[i] > ratings[i + 1])
i++;
tmp2 = i - top;
// 递减相加,也是等差数列
sum += tmp2 * (tmp2 - 1) / 2;
// 最后加上顶峰的糖果数,取左右最大值
sum += max(tmp1, tmp2);
}
return sum;
}
};罗马数字转整数
解法:模拟
因为考虑到罗马数字的组合,遍历时如果当前罗马数字可以与后面的罗马数字进行组合,加上当前罗马数字对应整数的相反数就行了,不需要把下一个罗马数字给加上(可能他也可以与它下一个罗马数字组合)
cpp
class Solution
{
public:
int romanToInt(string s)
{
unordered_map<char, int> hash;
hash.insert({'I', 1});
hash.insert({'V', 5});
hash.insert({'X', 10});
hash.insert({'L', 50});
hash.insert({'C', 100});
hash.insert({'D', 500});
hash.insert({'M', 1000});
int n = s.size(), sum = 0;
for (int i = 1; i < n; i++)
{
char s1 = s[i - 1], s2 = s[i];
if (hash[s1] < hash[s2])
sum += -hash[s1];
else
sum += hash[s1];
}
// 加上最后一个
return sum + hash[s[n - 1]];
}
};整数转罗马数字
解法:模拟
个,十,百,千的数字,作为数组下标(提前创建数组储存)找到对应的罗马数字
cpp
class Solution
{
public:
string intToRoman(int num)
{
string thousand[4] = {"", "M", "MM", "MMM"};
string hundred[10] = {"", "C", "CC", "CCC", "CD", "D", "DC", "DCC", "DCCC", "CM"};
string ten[10] = {"", "X", "XX", "XXX", "XL", "L", "LX", "LXX", "LXXX", "XC"};
string one[10] = {"", "I", "II", "III", "IV", "V", "VI", "VII", "VIII", "IX"};
return thousand[num / 1000] + hundred[num / 100 % 10] + ten[num / 10 % 10] + one[num % 10];
}
};最后一个单词的长度
解法:模拟
把最后的空格遍历掉再统计单词长度
cpp
class Solution
{
public:
int lengthOfLastWord(string s)
{
int n = s.size(), ret = 0;
int i = n - 1;
while (i >= 0 && s[i] == ' ')
i--;
while (i >= 0 && s[i] != ' ')
{
ret++;
i--;
}
return ret;
}
};最长公共前缀
解法:模拟
以第一个字符串为参照物,从第一个字符开始与后面字符串的字符进行比较,都相等则找到了一个字符,使用 ret 进行收集,往后遍历;都不相等则找到了最长公共前缀返回 ret
cpp
class Solution
{
public:
string longestCommonPrefix(vector<string> &strs)
{
int n = strs.size();
string ret;
for (int i = 0; i < strs[0].size(); i++)
{
char ch = strs[0][i];
for (int j = 1; j < n; j++)
{
if (ch != strs[j][i] || strs[j].size() < i + 1)
{
return ret;
}
}
ret += ch;
}
return ret;
}
};反转字符串中的单词
解法:双指针
从后往前遍历,收集完整单词的前后位置,通过 substr 还原后进行收集起来(并在每个单词后添加空格)
cpp
class Solution
{
public:
string reverseWords(string s)
{
// 删除首尾空字符
int i = 0, n = s.size();
while (i < n && s[i] == ' ')
i++;
int j = n - 1;
while (j >= 0 && s[j] == ' ')
j--;
s = s.substr(i, j - i + 1);
n = s.size();
i = j = n - 1;
string ret;
while (i >= 0)
{
while (i >= 0 && s[i] != ' ')
i--; // 找首字符位置
ret += s.substr(i + 1, j - i);
if (i > 0)
ret += ' ';
while (i >= 0 && s[i] == ' ')
i--; // 找尾字符位置
j = i;
}
return ret;
}
};文本左右对齐
解法:模拟
本题适合分组循环:
- 外层循环负责数据初始化和结果统计
使用 start 标记当前遍历的起始位置,sumWidth 统计当前字符串长度:从 start 开始找小于等于 maxWidth 的符合要求的字符串(统计时每个单词之间有一个空格,也要统计)
内层找到最远地方 i 之后,计算剩余字符(空格)的个数和单词之间的间隙 gap,分情况统计:
- 如果当前只有一个单词或者是最后一行了:按照 单词1 空格 单词2...的顺序排列(使用 使用 join),后面的字符都使用空格进行填充
- 否则,计算每个gap平均需要填充的空格 avg (这里需要 +1,把默认单词之间需要使用空格隔开这一个加上)和 前面有多个间隙可以额外多一个空格(如果某一行单词间的空格不能均匀分配,则左侧放置的空格数要多于右侧的空格数)
- 内层循环只负责遍历,找出最远的地方在哪
cpp
class Solution
{
public:
vector<string> fullJustify(vector<string> &words, int maxWidth)
{
auto join = [&](int start, int end, const string &sep) -> string
{
string res;
for (int i = start; i < end; i++)
{
if (i > start)
{
res += sep;
}
res += words[i];
}
return res;
};
int n = words.size();
vector<string> ret;
int i = 0;
while (i < n)
{
// 从start的下一个位置开始枚举长度(方便单词之间一个空格的收集)
int start = i, sumWidth = words[i++].size();
// 细节:可以等于maxWidth
while (i < n && sumWidth + words[i].size() + 1 <= maxWidth)
{
sumWidth += words[i].size() + 1;
i++;
}
// 计算剩下需要补充的空格(不包括之前单词之间统计的一个空格)和单词之间的空隙
int remainWidth = maxWidth - sumWidth, gap = i - start - 1;
string s;
// 一个单词或者是最后一行的情况
if (gap == 0 || i == n)
{
// 提取封装好单词与空格的添加情况,因为后面也需要用到
s += join(start, i, " ");
string space(remainWidth, ' ');
s += space;
ret.push_back(s);
continue;
}
// 统计每个空隙需要添加多少空格,同时看看需要前面几个空隙多一个空格(有不均分的情况)
int avg = remainWidth / gap, tmp = remainWidth % gap;
// 添加空格不要忘了本身即是不添加空格,默认也是有一个空格的!
string space(avg + 1, ' ');
// 前tmp个gap多1个空格
s += join(start, start + tmp + 1, space + " ");
// 记得先添加空格
s += space;
// 再对剩下gap的按照avg填充
s += join(start + tmp + 1, i, space);
ret.push_back(s);
}
return ret;
}
};验证回文串
解法:双指针
思路1:先还原成符合题目的字符串,再验证是否是回文串
思路2:边遍历该字符串是否符合要求的同时验证是否是回文串
python
class Solution:
def isPalindrome(self, s: str) -> bool:
# 边遍历边判断
i,j = 0,len(s)-1
ch_i,ch_j = '',''
while i<j:
while i<j and not ((s[i]>='a' and s[i]<='z') or (s[i]>='0' and s[i]<='9') or (s[i]>='A' and s[i]<='Z')):
i+=1
ch_i = s[i]
if s[i]>='A' and s[i]<='Z':
ch_i = chr(ord(s[i])+32)
while i<j and not ((s[j]>='a' and s[j]<='z') or (s[j]>='0' and s[j]<='9') or (s[j]>='A' and s[j]<='Z')):
j-=1;
ch_j = s[j]
if s[j]>='A' and s[j]<='Z':
ch_j = chr(ord(s[j])+32)
if ch_i != ch_j:
return False
i+=1
j-=1
return True
# ret = ""
# for i in range(0,len(s)):
# if s[i]>='A' and s[i]<='Z':
# ret += chr(ord(s[i])+32)
# elif (s[i]>='a' and s[i]<='z') or (s[i]>='0' and s[i]<='9'):
# ret+=s[i]
# i,j = 0,len(ret)-1
# while i<j:
# if ret[i] != ret[j]:
# break;
# i+=1
# j-=1
# if i<j:
# return False
# else:
# return True
盛最多水的容器
解法:双指针
定义两个指针执行开始和末尾,往中间边移动边收集最大面积,谁小谁移动(为了找更大的值组成最大面积)
cpp
class Solution {
public:
int maxArea(vector<int>& height) {
int n = height.size();
int i = 0,j = n - 1,sum = 0;
while(i < j)
{
sum = max((j-i)*min(height[i],height[j]),sum);
height[i] < height[j] ? i++: j--;
}
return sum;
}
};三数之和
解法:双指针
与两数之和类似,但你是要在遍历整个数组的过程中进行两树之和
主要考怎么去重的问题:先排序,再遍历时如果与上一个相邻的数相等,要循环tiao
cpp
class Solution
{
public:
vector<vector<int>> threeSum(vector<int> &nums)
{
int n = nums.size();
if (n < 3)
return {};
sort(nums.begin(), nums.end());
vector<vector<int>> ret;
for (int i = 0; i < n - 2; i++)
{
// 去重
if (i - 1 >= 0 && nums[i] == nums[i - 1])
continue;
int j = i + 1, k = n - 1;
// 加上最小的两个数大于0,就没有找的必要了
if (nums[i] + nums[i + 1] + nums[i + 2] > 0)
break;
// 加上最大的两个数小于0,i变大有机会等于0
if (nums[i] + nums[n - 1] + nums[n - 2] < 0)
continue;
while (j < k)
{
int sum = nums[i] + nums[j] + nums[k];
if (sum < 0)
j++;
else if (sum > 0)
k--;
else
{
ret.push_back({nums[i], nums[j], nums[k]});
j++;
k--;
// 去重
while (j < k && nums[j] == nums[j - 1])
j++;
while (j < k && nums[k] == nums[k - 1])
k--;
;
}
}
}
return ret;
}
};长度最小子数组
解法:滑动窗口
cpp
class Solution
{
public:
int minSubArrayLen(int target, vector<int> &nums)
{
int ret = INT_MAX, sum = 0, n = nums.size();
for (int i = 0, j = 0; i < n; i++)
{
sum += nums[i];
while (sum >= target)
{
ret = min(ret, i - j + 1);
sum -= nums[j];
j++;
}
}
return ret == INT_MAX ? 0 : ret;
}
};串联所有单词的子串
解法:滑动窗口
使用两个哈希表,hash1储存 words 中 word 出现的个数情况,hash2用来遍历时记录当前子串的个数情况
因为每个单词长度是一致的,所有以 [0, 单词长度] 为起点找目标子串,也就是进行遍历
定义 left 和 right 来移动窗口,从 i 位置为起点
入窗口:先把当前单词 s.substr(left,n) 记录在哈希表中,如果个数小于等于 hash1中储存该单词的个数,说明加入的单词是有效的,count++
更新结果:如果统计在哈希表中的单词个数等于 words 中的单词个数,就要看看是不是都是有效单词,也就是 count 是否等于 words 中的单词个数:等于就是找到了,进行统计
出窗口:先让 hash2 中储存该单词 s.substr(right,n)移除(进行 -- 操作),如果移除后 hash2对应单词的个数 小于 hash1储存该单词对应的个数(窗口内此时如果有重复的单词,该条件就不会成立),说明移除的是符合要求的单词,count --
cpp
class Solution
{
public:
vector<int> findSubstring(string s, vector<string> &words)
{
unordered_map<string, int> hash;
vector<int> ans;
for (auto &ch : words)
{
hash[ch]++;
}
int n = words[0].size(), m = words.size(), k = s.size();
// 以 [0,n]为起点找子串
for (int i = 0; i < n; i++)
{
unordered_map<string, int> hash1;
for (int left = i, right = i, count = 0; right < k; right += n)
{
string in = s.substr(right, n);
hash1[in]++;
// 满足条件说明入窗口的字符串是有效的
if (hash1[in] <= hash[in])
{
count++;
}
if (right - left + n == n * m)
{
if (count == words.size())
{
ans.push_back(left);
}
string out = s.substr(left, n);
hash1[out]--;
// 判断结果成立,出窗口的字符串是有效的
if (hash1[out] < hash[out])
{
count--;
}
left += n;
}
}
}
return ans;
}
};最小覆盖子串
解法:滑动窗口
此题与上题类似:但从字符串变成了字符,少了一步遍历,做起来就变简单了
cpp
class Solution
{
public:
string minWindow(string s, string t)
{
int n = s.size(), m = t.size();
unordered_map<char, int> hash1, hash2;
for (auto &ch : t)
hash1[ch]++;
// begin为n,找不到符合的子串就返回空
int begin = n, len = n, cnt = 0;
for (int i = 0, j = 0; i < n; i++)
{
char ch = s[i];
hash2[ch]++;
if (hash2[ch] <= hash1[ch])
cnt++;
while (cnt == m)
{
if (i - j + 1 <= len)
{
begin = j;
len = i - j + 1;
}
ch = s[j++];
hash2[ch]--;
if (hash2[ch] < hash1[ch])
cnt--;
}
}
return s.substr(begin, len);
}
};有趣的数独
解法:模拟
使用三个数组对应 行,列,3*3格,一次遍历就能得到结果
cpp
class Solution {
public:
bool row[9][10]={false};
bool col[9][10]={false};
bool grid[3][3][10]={false};
bool isValidSudoku(vector<vector<char>>& board)
{
for(int i=0;i<board.size();i++)
{
for(int j=0;j<board[i].size();j++)
{
if(board[i][j]!='.')
{
int tmp=board[i][j]-'0';
if(!row[i][tmp]&&!col[j][tmp]&&!grid[i/3][j/3][tmp])
{
row[i][tmp]=col[j][tmp]=grid[i/3][j/3][tmp]=true;
}
else
{
return false;
}
}
}
}
return true;
}
};螺旋矩阵
解法:模拟
标记法
由题意得:走法是:右 下 左 上,可以向作 dfs/bfs 那样创建 dx[4] dy[4] 来控制走的方向
创建一个相同的矩阵用来标记(或者直接在原数组中修改),如果走到该位置为 true 说明之前走过了要调转到之前的位置,换方向走
如果收集的个数等于原矩阵的个数,说明得到了答案
cpp
class Solution
{
public:
vector<int> spiralOrder(vector<vector<int>> &matrix)
{
int n = matrix.size(), m = matrix[0].size();
vector<int> ret;
bool vis[11][11];
memset(vis, false, sizeof(vis));
int i = 0, j = 0, dis = 0;
int dx[4] = {0, 1, 0, -1};
int dy[4] = {1, 0, -1, 0};
while (ret.size() < n * m)
{
if (i >= 0 && i < n && j >= 0 && j < m)
{
if (!vis[i][j])
{
vis[i][j] = true;
ret.push_back(matrix[i][j]);
}
else
{
i -= dx[dis];
j -= dy[dis];
dis = (dis + 1) % 4;
}
}
else
{
i -= dx[dis];
j -= dy[dis];
dis = (dis + 1) % 4;
}
i += dx[dis];
j += dy[dis];
}
return ret;
}
};不标记法
规律:向右 左 走的时候,是一个从 m 步开始的递减序列
从下 上 走的时候,是一个从 n-1 步开始的递减序列
所有从 [0,-1] 位置开始控制走的步数,就不会越界,也不会担心走的位置是之前走过的
cpp
class Solution
{
public:
vector<int> spiralOrder(vector<vector<int>> &matrix)
{
int n = matrix.size(), m = matrix[0].size();
vector<int> ret;
// 从 [0,-1]位置开始
int i = 0, j = -1, dis = 0, cnti = m, cntj = n - 1;
int dx[4] = {0, 1, 0, -1};
int dy[4] = {1, 0, -1, 0};
while (ret.size() < n * m)
{
for (int k = 0; k < cnti; k++)
{
i += dx[dis], j += dy[dis];
ret.push_back(matrix[i][j]);
}
// 每4次为一个循环
dis = (dis + 1) % 4;
for (int k = 0; k < cntj; k++)
{
i += dx[dis], j += dy[dis];
ret.push_back(matrix[i][j]);
}
dis = (dis + 1) % 4;
cnti--, cntj--;
}
return ret;
}
};旋转图像
解法:模拟
顺时针旋转90度后的结果,原第一列变成第一行,原第一行变成最后一列...
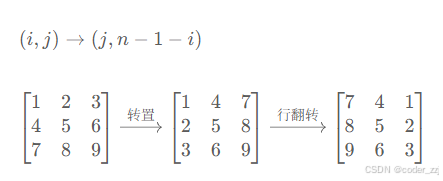
转置遍历:遍历每一行,只要当前列值不超过当前行值就继续 swap 交换,也就是在正常遍历列时加上 j < i 就能实现
cpp
class Solution
{
public:
void rotate(vector<vector<int>> &matrix)
{
int n = matrix.size();
// for(int i=0;i<n;i++)
// for(int j=0;j<i;j++)//j<i 实现出对角线翻转
// swap(matrix[i][j],matrix[j][i]);
// for(int i=0;i<n;i++)
// {
// int b=0,e=n-1;
// while(b<e)
// swap(matrix[i][b++],matrix[i][e--]);
// }
for (int i = n - 1; i >= 0; i--)
{
for (int j = 0; j < i; j++) // j<i 实现出对角线翻转
swap(matrix[i][j], matrix[j][i]);
reverse(matrix[i].begin(), matrix[i].end());
}
}
};以上便是全部内容,有问题欢迎在评论区指正,感谢观看!