机器学习中的决策树

文章目录

[一树模型](#一树模型)
[二决策树的训练与测试](#二决策树的训练与测试)
- [2.1 核心问题](#2.1 核心问题)
- [2.2 核心目标](#2.2 核心目标)
- - [2.3 关键衡量逻辑](#2.3 关键衡量逻辑)
[三衡量标准](#三衡量标准)
- [3.1 熵的定义](#3.1 熵的定义)
- [3.2 熵的计算公式](#3.2 熵的计算公式)
- [3.3 实例验证（A集合 vs B集合）](#3.3 实例验证（A集合 vs B集合）)
- [3.4 熵在决策树分类任务中的作用](#3.4 熵在决策树分类任务中的作用)
[四决策树构造实例](#四决策树构造实例)
[五决策树算法](#五决策树算法)
- [5.1 ID3 算法](#5.1 ID3 算法)
- [5.2 C4.5 算法](#5.2 C4.5 算法)
- [5.3 CART 算法](#5.3 CART 算法)
[六决策树剪枝策略](#六决策树剪枝策略)
- [6.1 为什么要剪枝？------ 过拟合风险的根源](#6.1 为什么要剪枝？—— 过拟合风险的根源)
- [6.2 剪枝策略的分类：预剪枝 vs 后剪枝](#6.2 剪枝策略的分类：预剪枝 vs 后剪枝)
- - [6.2.1 预剪枝（Pre - pruning）：生长过程中主动限制](#6.2.1 预剪枝（Pre - pruning）：生长过程中主动限制)
  - [6.2.2 后剪枝（Post - pruning）：生长完成后被动修剪](#6.2.2 后剪枝（Post - pruning）：生长完成后被动修剪)
- [6.3 预剪枝与后剪枝的工程选择逻辑](#6.3 预剪枝与后剪枝的工程选择逻辑)
[七决策树代码实现和可视化](#七决策树代码实现和可视化)
- [7.1 决策树代码实现](#7.1 决策树代码实现)
- [7.2 决策树模型可视化](#7.2 决策树模型可视化)
- [7.3 决策边界可视化](#7.3 决策边界可视化)
- [7.4 决策树的正则化（剪枝）](#7.4 决策树的正则化（剪枝）)
- [7.5 决策树模型的不稳定性](#7.5 决策树模型的不稳定性)
[八回归树模型(决策树用于回归任务)](#八回归树模型(决策树用于回归任务))
- [8.1 决策树模型创建和绘制](#8.1 决策树模型创建和绘制)
- [8.2 不同深度切分可视化](#8.2 不同深度切分可视化)
- [8.3 设置最小叶子节点数效果](#8.3 设置最小叶子节点数效果)

一树模型

决策树：从根节点开始一步步走到叶子节点(决策)。
所有的数据最终都会落到叶子节点，既可以做分类也可以做回归。
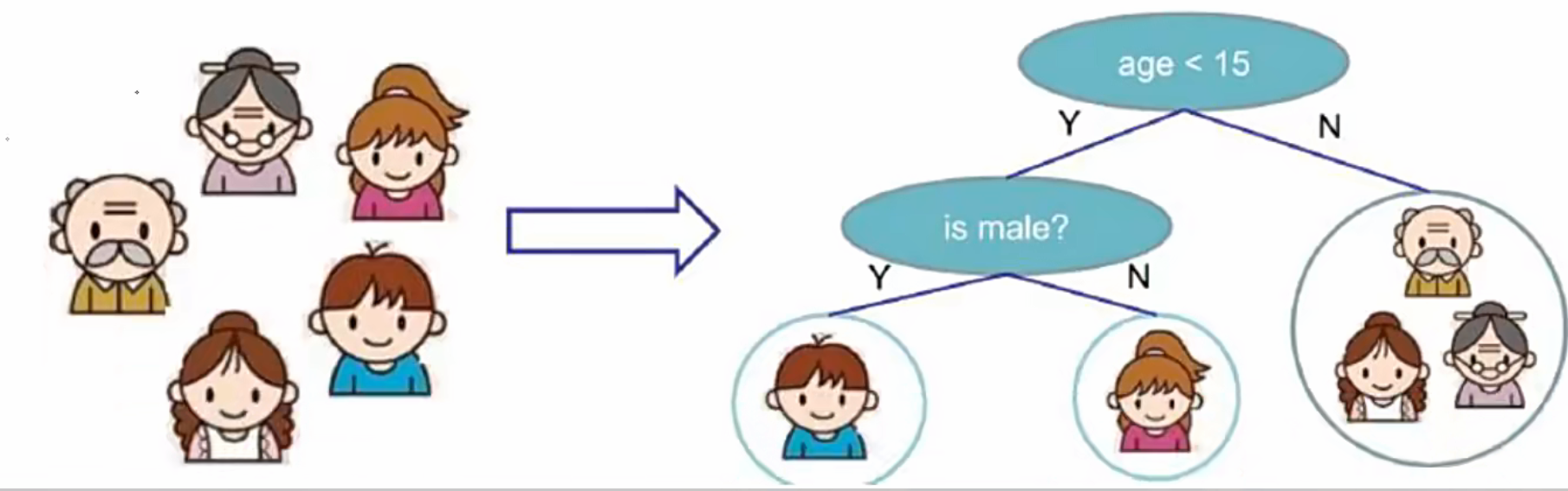
树的组成
- 根节点：第一个选择点
- 非叶子节点与分支
- 叶子节点：最终的决策结果

二决策树的训练与测试

训练阶段：从给定的数据集构造出一棵树（从根节点开始选择特征，如何进行特征切人）
测试阶段：根据构造出来的树模型从上到下走一遍
决策树的难点在于树的构建。

决策树切分特征

2.1 核心问题

决策树构建中，根节点及后续内部节点的特征选择与切分规则是关键问题。具体需解决：

如何确定"当前节点该用哪个特征进行分支"？
该特征的"切分阈值/方式"如何确定？
分支后子节点的特征选择逻辑是什么？（递归地重复上述过程）

2.2 核心目标

通过量化评估指标，衡量不同特征分支后的分类效果，筛选出"最优特征+最优切分方式"，作为当前节点的分支依据；并以此为基础，递归地为子节点选择特征，直至满足停止条件（如纯度足够高、样本量过小等）。

2.3 关键衡量逻辑

为实现"分类效果好"的目标，需引入不纯度度量指标（如信息增益、信息增益比、基尼系数等），其核心思想是：

计算某特征分支前后的"数据不纯度变化"------若分支后子节点的类别更集中（不纯度降低越多），则说明该特征对分类的"区分能力"越强。
选择使"不纯度下降幅度最大"（或增益最高）的特征作为当前节点的分支特征，对应的切分方式即为最优切分策略。
简言之，决策树的特征切分是一个**"以不纯度最小化为导向，递归选择最优特征与切分方式"**的过程，最终实现"自顶向下逐步优化分类效果"的树结构构建。

三衡量标准

3.1 熵的定义

熵是信息论中用于量化随机变量不确定性的核心指标，在决策树场景下，可理解为"数据集内类别分布的混乱程度"：

若数据集仅含单一类别（如全为"1"），则不确定性极低，熵值趋近于0；
若数据集包含多种类别且分布均匀（如杂货市场商品种类繁多），则不确定性极高，熵值趋近于最大值。

3.2 熵的计算公式

对于离散型随机变量 X X X，其熵 H ( X ) H(X) H(X) 的数学表达式为： H ( X ) = − ∑ i = 1 n p i ⋅ log ⁡ 2 p i H(X) = -\sum_{i=1}^{n} p_i \cdot \log_2 p_i H(X)=−∑i=1npi⋅log2pi

其中：

n n n：数据集的类别总数；
p i p_i pi：第 i i i 个类别的出现概率（即该类别样本数占总样本数的比例）；
对数底数通常取2（单位为"比特"），也可根据需求选自然对数（单位为"纳特"）或10为底（单位为"哈特利"）。

3.3 实例验证（A集合 vs B集合）

以图中两个集合为例，直观展示熵的差异：

A集合 ： [ 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 2 , 2 ] [1,1,1,1,1,1,1,1,2,2] [1,1,1,1,1,1,1,1,2,2]（共10个样本，类别1占比 8 / 10 = 0.8 8/10=0.8 8/10=0.8，类别2占比 2 / 10 = 0.2 2/10=0.2 2/10=0.2）
计算得：
H ( A ) = − ( 0.8 ⋅ log ⁡ 2 0.8 + 0.2 ⋅ log ⁡ 2 0.2 ) ≈ 0.7219 H(A) = -(0.8 \cdot \log_2 0.8 + 0.2 \cdot \log_2 0.2) \approx 0.7219 H(A)=−(0.8⋅log20.8+0.2⋅log20.2)≈0.7219
B集合 ： [ 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 1 ] [1,2,3,4,5,6,7,8,9,1] [1,2,3,4,5,6,7,8,9,1]（共10个样本，类别1占比 2 / 10 = 0.2 2/10=0.2 2/10=0.2，其余8个类别各占 1 / 10 = 0.1 1/10=0.1 1/10=0.1）
计算得：
H ( B ) = − ( 0.2 ⋅ log ⁡ 2 0.2 + 8 × 0.1 ⋅ log ⁡ 2 0.1 ) ≈ 3.1219 H(B) = -(0.2 \cdot \log_2 0.2 + 8 \times 0.1 \cdot \log_2 0.1) \approx 3.1219 H(B)=−(0.2⋅log20.2+8×0.1⋅log20.1)≈3.1219
可见，A集合因类别少、分布相对集中，熵值更低（不确定性更小）；B集合因类别多、分布分散，熵值更高（不确定性更大）。

3.4 熵在决策树分类任务中的作用

在决策树的"特征切分"环节，熵是衡量分支效果的关键指标：

目标是通过节点分裂，让子节点的类别分布更"纯净"（即熵值尽可能小）。例如，若某特征分裂后，子节点的熵显著低于父节点，说明该特征能有效区分不同类别，应优先选择。
具体操作中，会计算"父节点熵 - 子节点加权平均熵"（即信息增益），选择信息增益最大的特征作为分裂依据------这一逻辑正是ID3算法的核心原理。

熵的本质是"数据不确定性的量化工具"，其在决策树中承担着"指导特征选择、优化分类纯度"的关键角色，是实现"自顶向下逐步分类"的核心衡量标准之一。

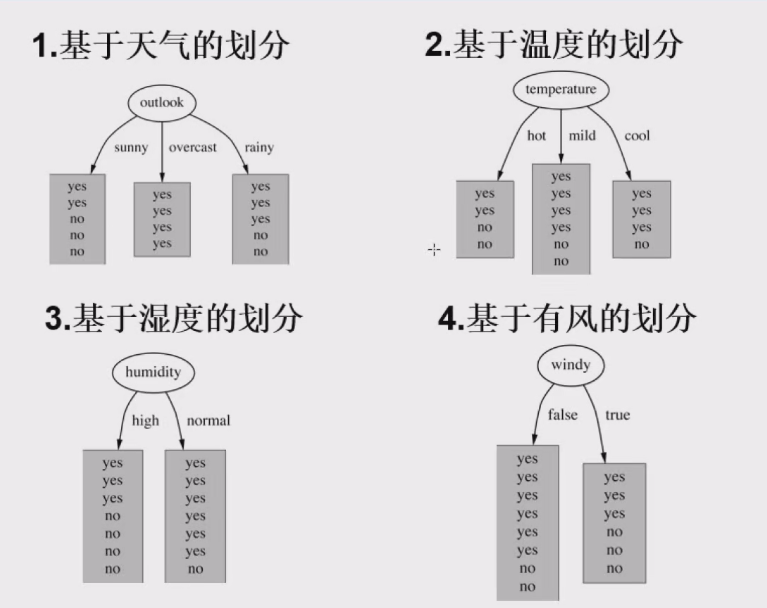
四决策树构造实例

数据：14天打球情况
特征：4种环境变化
目标：构造决策树

outlook	temperature	humidity	windy	play
sunny	hot	high	FALSE	no
sunny	hot	high	TRUE	no
overcast	hot	high	FALSE	yes
rainy	mild	high	FALSE	yes
rainy	cool	normal	FALSE	yes
rainy	cool	normal	TRUE	no
overcast	cool	normal	TRUE	yes
sunny	mild	high	FALSE	no
sunny	cool	normal	FALSE	yes
rainy	mild	normal	FALSE	yes
sunny	mild	normal	TRUE	yes
overcast	mild	high	TRUE	yes
overcast	hot	normal	FALSE	yes
rainy	mild	high	TRUE	no

划分方式：4种

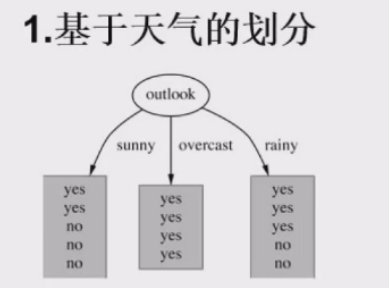
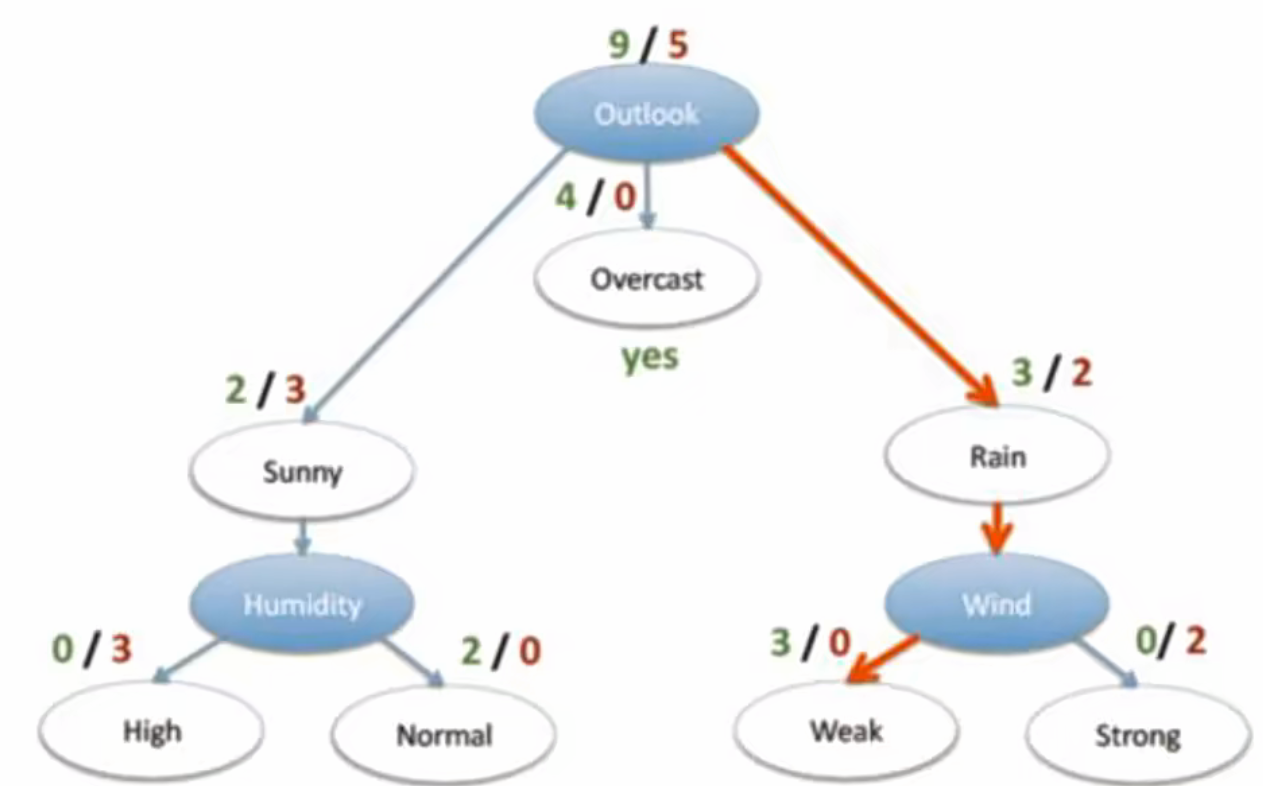
在历史数据（14天）中，有9天打球、5天不打球，此时的熵计算如下：
− 9 14 log ⁡ 2 9 14 − 5 14 log ⁡ 2 5 14 = 0.940 -\frac{9}{14}\log_2\frac{9}{14} - \frac{5}{14}\log_2\frac{5}{14} = 0.940 −149log2149−145log2145=0.940

特征分析（以outlook为例）
当 Outlook = sunny 时，熵值为 − 2 5 log ⁡ 2 2 5 − 3 5 log ⁡ 2 3 5 = 0.971 -\frac{2}{5}\log_2\frac{2}{5} - \frac{3}{5}\log_2\frac{3}{5} = 0.971 −52log252−53log253=0.971
当 Outlook = overcast 时，熵值为 − 4 4 log ⁡ 2 4 4 − 4 4 log ⁡ 2 4 4 = 0 -\frac{4}{4}\log_2\frac{4}{4} - \frac{4}{4}\log_2\frac{4}{4} = 0 −44log244−44log244=0
当 Outlook = rainy 时，熵值为 − 2 5 log ⁡ 2 2 5 − 3 5 log ⁡ 2 3 5 = 0.971 -\frac{2}{5}\log_2\frac{2}{5} - \frac{3}{5}\log_2\frac{3}{5} = 0.971 −52log252−53log253=0.971

特征概率统计
根据数据统计，outlook 取值分别为 sunny、overcast、rainy 的概率分别为：
5 14 \frac{5}{14} 145、 4 14 \frac{4}{14} 144、 5 14 \frac{5}{14} 145
熵值计算
基于上述概率，outlook 对应的熵值计算为：
5 14 × 0.971 + 4 14 × 0 + 5 14 × 0.971 = 0.693 \frac{5}{14} \times 0.971 + \frac{4}{14} \times 0 + \frac{5}{14} \times 0.971 = 0.693 145×0.971+144×0+145×0.971=0.693
（注：其他特征的信息增益参考值：gain(temperature)=0.029、gain(humidity)=0.152、gain(windy)=0.048）
信息增益分析
系统的熵值从原始的 0.940 0.940 0.940 下降到 0.693 0.693 0.693，因此信息增益为：
0.940 − 0.693 = 0.247 0.940 - 0.693 = 0.247 0.940−0.693=0.247
特征选择逻辑

通过同样的方式计算其他特征的信息增益后，选择信息增益最大的特征(outlook)作为分裂节点；后续再对剩余特征重复该过程，直至完成决策树构造。

五决策树算法

5.1 ID3 算法

核心思想 ：以「信息增益（Information Gain, IG）」作为特征选择的衡量标准，优先选择能最大化"信息增益"的特征来分裂节点。
信息增益的定义 ：表示"使用某特征分裂后，系统不确定性的减少程度"。公式为：
IG ( D , a ) = H ( D ) − H ( D ∣ a ) \text{IG}(D, a) = H(D) - H(D|a) IG(D,a)=H(D)−H(D∣a)
其中， H ( D ) H(D) H(D) 是数据集 D D D 的原始熵（不确定性）， H ( D ∣ a ) H(D|a) H(D∣a) 是按特征 a a a 分裂后的条件熵（分裂后各子节点的加权平均熵）。
局限性 ：
信息增益易偏向"取值多的特征"（因为特征分支越多，条件熵 H ( D ∣ a ) H(D|a) H(D∣a) 越小，信息增益越大）。例如，"编号"这类唯一标识特征，虽无实际预测价值，但会因分支多而获得高信息增益，导致过拟合。

5.2 C4.5 算法

核心改进 ：针对 ID3 的"偏向多值特征"问题，提出「信息增益率（Gain Ratio） 」作为新的衡量标准，公式为：
GainRatio ( D , a ) = IG ( D , a ) SplitInfo ( D , a ) \text{GainRatio}(D, a) = \frac{\text{IG}(D, a)}{\text{SplitInfo}(D, a)} GainRatio(D,a)=SplitInfo(D,a)IG(D,a)
其中， SplitInfo ( D , a ) \text{SplitInfo}(D, a) SplitInfo(D,a) 是"特征 a a a 自身的熵"，用于惩罚"取值多的特征"（分支越多， SplitInfo \text{SplitInfo} SplitInfo 越大，增益率越小）。
优势：通过"信息增益率"平衡了特征的价值与复杂度，减少了多值特征的干扰，提升了模型泛化能力。
额外特点：支持连续特征离散化、可处理缺失值，是 ID3 的经典升级版。

5.3 CART 算法

核心差异 ：不再使用"信息论"指标（如熵、信息增益），而是采用「Gini 系数（基尼系数）」作为特征选择的衡量标准，且支持"分类+回归"任务。
Gini 系数的定义 ：表示"从数据集中随机选两个样本，其类别不一致的概率"，公式为：
Gini ( p ) = ∑ k = 1 K p k ( 1 − p k ) = 1 − ∑ k = 1 K p k 2 \text{Gini}(p) = \sum_{k=1}^K p_k (1 - p_k) = 1 - \sum_{k=1}^K p_k^2 Gini(p)=k=1∑Kpk(1−pk)=1−k=1∑Kpk2

其中， p k p_k pk 是第 k k k 类样本的比例， K K K 是类别总数。Gini 系数越小，数据纯度越高（同类样本越集中）。
分裂规则：选择使"Gini 系数减少最多"的特征来分裂节点（即最大化 Gini 纯度提升）。
优势与应用：
- 计算效率高于信息增益（无需对数运算）；
- 支持"二叉树"结构（每次分裂产生两个子节点），便于剪枝和防止过拟合；
- 广泛应用于分类（如 sklearn 的 DecisionTreeClassifier）和回归（DecisionTreeRegressor）场景。
三种算法的发展脉络体现了"从单一指标到综合优化""从理论到工程实践"的演进：ID3 开创信息增益思路 → C4.5 解决多值特征偏差 → CART 拓展任务类型并优化计算效率。

六决策树剪枝策略

6.1 为什么要剪枝？------ 过拟合风险的根源

决策树的核心缺陷是"过拟合倾向"：若不对生长过程约束，树会持续分裂至"每个叶子节点仅含少量甚至单个样本"（即"完全拟合训练数据"）。这种情况下，模型会记住训练数据的噪声和细节（而非 generalize 到真实规律），对新数据的预测性能急剧下降。
简言之，剪枝的本质是通过简化树结构，降低模型复杂度，从而提升泛化能力（避免"为了拟合训练数据而牺牲对新数据的适应性"）。

6.2 剪枝策略的分类：预剪枝 vs 后剪枝

决策树剪枝的核心分歧在于**"何时停止/干预树的分裂"**，由此分为两类主流策略：

6.2.1 预剪枝（Pre - pruning）：生长过程中主动限制

预剪枝是在构建决策树时，提前设定"终止分裂的条件"，阻止树过度生长。常见触发条件包括：

深度限制 ：设定树的最大深度（如 max_depth=3），达到深度后停止分裂；
最小样本量约束 ：要求节点分裂前必须包含足够样本（如 min_samples_split=10，即节点样本数少于10则不分裂）；
纯度阈值：若节点分裂后纯度提升不足（如信息增益小于阈值），则停止分裂。

优点：计算效率高（无需生成完整大树再剪枝），能有效控制模型复杂度；
缺点：可能因"过早停止"错过重要分裂（欠拟合风险），需通过交叉验证调整参数。

6.2.2 后剪枝（Post - pruning）：生长完成后被动修剪

后剪枝是先生成完整的"最大树"（允许树充分分裂至无法再分），再从下往上逐步剪除无效分支。典型方法如「代价复杂度剪枝（CCP）」，其核心逻辑是：

定义"剪枝收益"：比较"剪枝前后模型的泛化误差变化"（通常用"测试集误差"或"交叉验证误差"衡量）；
若剪枝后泛化误差未显著上升（或上升幅度在可接受范围内），则剪掉该分支；反之保留。

优点：能充分利用训练数据的信息，找到更优的剪枝点（相比预剪枝更灵活）；
缺点：计算成本高（需先生成完整大树，再遍历所有可能的剪枝组合），且需大量数据支撑泛化误差估计。

6.3 预剪枝与后剪枝的工程选择逻辑

在实际应用中，预剪枝更"实用高效"（适合大规模数据或实时性要求高的场景），而后剪枝更"精准鲁棒"（适合数据量充足、对精度要求高的场景）。两者并非对立，也可结合使用（如先用预剪枝控制规模，再用后剪枝微调）。
综上，图中内容本质是对"决策树过拟合治理"的专业解读：通过「预剪枝（生长中约束）」和「后剪枝（生长后修剪）」两种策略，平衡"模型复杂度"与"泛化能力"，解决决策树"易过拟合"的核心痛点。

七决策树代码实现和可视化

7.1 决策树代码实现

python 复制代码

# -*- coding: utf-8 -*-

# 导入所需的库
from matplotlib.font_manager import FontProperties  # 用于处理matplotlib中的字体
import matplotlib.pyplot as plt  # Python的绘图库
from math import log  # 用于计算对数
import operator  # 用于排序操作

# ==================== 决策树构建相关函数 ====================

def createDataSet():
    """
    函数功能：创建一个简单的数据集用于测试。
    数据集包含4个特征（年龄、工作、房子、贷款）和1个标签（是否放贷）。
    返回值：
        dataSet: 数据集，列表的列表，每个子列表代表一个样本。
        labels: 特征标签，列表，每个元素代表一个特征的名称。
    """
    # 定义数据集，每一行代表一个样本，最后一列是类别标签
    dataSet = [[0, 0, 0, 0, 'no'],
               [0, 0, 0, 1, 'no'],
               [0, 1, 0, 1, 'yes'],
               [0, 1, 1, 0, 'yes'],
               [0, 0, 0, 0, 'no'],
               [1, 0, 0, 0, 'no'],
               [1, 0, 0, 1, 'no'],
               [1, 1, 1, 1, 'yes'],
               [1, 0, 1, 2, 'yes'],
               [1, 0, 1, 2, 'yes'],
               [2, 0, 1, 2, 'yes'],
               [2, 0, 1, 1, 'yes'],
               [2, 1, 0, 1, 'yes'],
               [2, 1, 0, 2, 'yes'],
               [2, 0, 0, 0, 'no']]
    # 定义每个特征对应的标签名称
    labels = ['F1-AGE', 'F2-WORK', 'F3-HOME', 'F4-LOAN']
    # 返回数据集和标签
    return dataSet, labels

def calcShannonEnt(dataset):
    """
    函数功能：计算给定数据集的香农熵。
    熵是度量数据集纯度的指标，熵越大，数据集的不确定性越高。
    参数：
        dataset: 数据集
    返回值：
        shannonEnt: 计算得到的香农熵
    """
    # 计算数据集中样本的总数
    numEntries = len(dataset)
    # 创建一个字典，用于统计每个类别出现的次数
    labelCounts = {}
    # 遍历数据集中的每个样本
    for featVec in dataset:
        # 获取当前样本的类别标签（最后一列）
        currentLabel = featVec[-1]
        # 如果该标签不在字典中，则初始化为0
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel] = 0
        # 该标签的计数加1
        labelCounts[currentLabel] += 1
    # 初始化香农熵为0
    shannonEnt = 0.0
    # 遍历标签计数字典中的每个类别
    for key in labelCounts:
        # 计算该类别在数据集中的概率
        prob = float(labelCounts[key]) / numEntries
        # 根据香农熵公式累加：-p*log2(p)
        shannonEnt -= prob * log(prob, 2)
    # 返回计算出的香农熵
    return shannonEnt

def splitDataSet(dataset, axis, value):
    """
    函数功能：按照给定特征的特征值划分数据集。
    参数：
        dataset: 待划分的数据集
        axis: 划分数据集所依据的特征的列索引
        value: 该特征的值
    返回值：
        retDataSet: 划分后的子数据集（已移除用于划分的特征列）
    """
    # 创建一个空列表，用于存储划分后的数据
    retDataSet = []
    # 遍历数据集中的每个样本
    for featVec in dataset:
        # 如果样本在指定特征(axis)上的值等于给定的值
        if featVec[axis] == value:
            # 切片获取该特征之前的所有特征
            reducedFeatVec = featVec[:axis]
            # 将该特征之后的所有特征扩展到列表中
            reducedFeatVec.extend(featVec[axis+1:])
            # 将处理好的样本（已移除axis列）添加到返回列表中
            retDataSet.append(reducedFeatVec)
    # 返回划分后的数据集
    return retDataSet

def chooseBestFeatureToSplit(dataset):
    """
    函数功能：选择最好的数据集划分特征。
    通过计算每个特征划分数据集后的信息增益，选择信息增益最大的特征。
    参数：
        dataset: 数据集
    返回值：
        bestFeature: 最佳特征的列索引
    """
    # 计算特征的数量（最后一列是标签，所以要减1）
    numFeatures = len(dataset[0]) - 1
    # 计算原始数据集的香农熵（基础熵）
    baseEntropy = calcShannonEnt(dataset)
    # 初始化最佳信息增益为0
    bestInfoGain = 0.0
    # 初始化最佳特征的索引为-1
    bestFeature = -1
    # 遍历所有特征
    for i in range(numFeatures):
        # 获取数据集中第i个特征的所有值
        featList = [example[i] for example in dataset]
        # 使用set去重，得到该特征所有可能的唯一值
        uniqueVals = set(featList)
        # 初始化新的条件熵为0
        newEntropy = 0.0
        # 遍历该特征的每个唯一值
        for value in uniqueVals:
            # 根据当前特征值划分数据集
            subDataSet = splitDataSet(dataset, i, value)
            # 计算子数据集的概率（权重）
            prob = len(subDataSet) / float(len(dataset))
            # 累加条件熵：权重 * 子集的熵
            newEntropy += prob * calcShannonEnt(subDataSet)
        # 计算信息增益 = 基础熵 - 条件熵
        infoGain = baseEntropy - newEntropy
        # 如果当前信息增益大于已记录的最佳信息增益
        if (infoGain > bestInfoGain):
            # 更新最佳信息增益
            bestInfoGain = infoGain
            # 更新最佳特征的索引
            bestFeature = i
    # 返回最佳特征的索引
    return bestFeature

def majorityCnt(classList):
    """
    函数功能：当数据集已经处理了所有属性，但类标签依然不是唯一的，
              采用多数表决的方法决定该叶子节点的分类。
    参数：
        classList: 类标签列表
    返回值：
        sortedClassCount[0][0]: 出现次数最多的类标签
    """
    # 创建一个字典，用于记录每个类标签出现的次数
    classCount = {}
    # 遍历类标签列表
    for vote in classList:
        # 如果标签不在字典中，初始化为0
        if vote not in classCount.keys():
            classCount[vote] = 0
        # 计数加1
        classCount[vote] += 1
    # 使用operator.itemgetter(1)按字典的值（即次数）进行降序排序
    sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
    # 返回出现次数最多的类标签
    return sortedClassCount[0][0]

def createTree(dataset, labels, featLabels):
    """
    函数功能：递归创建决策树。
    参数：
        dataset: 数据集
        labels: 数据集所有特征的标签列表
        featLabels: 用于存储决策树构建过程中实际使用的特征标签
    返回值：
        myTree: 构建好的决策树（字典结构）
    """
    # 取出数据集中所有样本的类别标签
    classList = [example[-1] for example in dataset]
    # 递归停止条件1：如果所有样本的类别完全相同，则停止划分，返回该类别
    if classList.count(classList[0]) == len(classList):
        return classList[0]
    # 递归停止条件2：如果遍历完所有特征，但类别仍不唯一，返回出现次数最多的类别
    if len(dataset[0]) == 1:
        return majorityCnt(classList)
    
    # 选择最佳划分特征的索引
    bestFeat = chooseBestFeatureToSplit(dataset)
    # 获取最佳特征的标签
    bestFeatLabel = labels[bestFeat]
    # 将当前使用的特征标签添加到featLabels中
    featLabels.append(bestFeatLabel)
    # 使用字典存储树结构，根节点是当前最佳特征标签
    myTree = {bestFeatLabel: {}}
    # 从labels列表中删除已使用的特征标签
    del labels[bestFeat]
    # 获取最佳特征列的所有值
    featValues = [example[bestFeat] for example in dataset]
    # 获取该特征的所有唯一值
    uniqueVals = set(featValues)
    # 遍历每个特征值，递归地构建子树
    for value in uniqueVals:
        # 因为labels在递归过程中会被修改，所以需要传入一个副本
        subLabels = labels[:]
        # 递归调用createTree，构建子树，并赋值给父节点的对应分支
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataset, bestFeat, value), subLabels, featLabels)
    # 返回构建好的决策树
    return myTree

# ==================== 决策树绘制相关函数 ====================

def getNumLeafs(myTree):
    """
    函数功能：递归获取决策树的叶子节点数目。
    参数：
        myTree: 决策树
    返回值：
        numLeafs: 叶子节点的总数
    """
    # 初始化叶子节点数为0
    numLeafs = 0
    # 获取树的第一个键（即根节点的特征标签）
    firstStr = next(iter(myTree))
    # 获取根节点对应的字典（子树）
    secondDict = myTree[firstStr]
    # 遍历子树的每个键（特征值）
    for key in secondDict.keys():
        # 如果该键对应的值是一个字典（说明是子树，不是叶子节点）
        if type(secondDict[key]).__name__ == 'dict':
            # 递归调用getNumLeafs，累加子树的叶子节点数
            numLeafs += getNumLeafs(secondDict[key])
        else: # 如果不是字典，说明是叶子节点
            # 叶子节点数加1
            numLeafs += 1
    # 返回总的叶子节点数
    return numLeafs

def getTreeDepth(myTree):
    """
    函数功能：递归获取决策树的深度。
    参数：
        myTree: 决策树
    返回值：
        maxDepth: 决策树的最大深度
    """
    # 初始化最大深度为0
    maxDepth = 0
    # 获取根节点标签
    firstStr = next(iter(myTree))
    # 获取子树字典
    secondDict = myTree[firstStr]
    # 遍历子树的每个键
    for key in secondDict.keys():
        # 如果是子树
        if type(secondDict[key]).__name__ == 'dict':
            # 当前深度 = 1 + 子树的深度
            thisDepth = 1 + getTreeDepth(secondDict[key])
        else: # 如果是叶子节点
            # 当前深度为1
            thisDepth = 1
        # 如果当前深度大于已记录的最大深度，则更新最大深度
        if thisDepth > maxDepth:
            maxDepth = thisDepth
    # 返回最大深度
    return maxDepth

def plotNode(nodeTxt, centerPt, parentPt, nodeType):
    """
    函数功能：绘制带箭头的注解，即树的节点。
    参数：
        nodeTxt: 节点显示的文本
        centerPt: 节点的中心坐标
        parentPt: 父节点的坐标
        nodeType: 节点的样式（决策节点或叶子节点）
    """
    # 定义箭头的样式
    arrow_args = dict(arrowstyle="<-")
    # 尝试加载中文字体，如果失败则使用默认字体并提示
    try:
        # 创建一个字体属性对象，指定字体文件路径和大小
        font = FontProperties(fname=r"C:\Windows\Fonts\simhei.ttf", size=14)
    except FileNotFoundError:
        print("字体文件未找到，将使用默认字体。中文可能显示为方框。")
        font = FontProperties(size=14)

    # 使用annotate函数绘制节点
    # xy: 箭头终点坐标, xycoords: 终点坐标系
    # xytext: 文本起点坐标, textcoords: 文本坐标系
    # va/ha: 垂直/水平对齐方式
    # bbox: 文本框样式, arrowprops: 箭头样式
    # fontproperties: 字体属性
    createPlot.ax1.annotate(nodeTxt, xy=parentPt,  xycoords='axes fraction',
                            xytext=centerPt, textcoords='axes fraction',
                            va="center", ha="center", bbox=nodeType, arrowprops=arrow_args,
                            fontproperties=font)

def plotMidText(cntrPt, parentPt, txtString):
    """
    函数功能：在父子节点之间的连线上添加特征值文本。
    参数：
        cntrPt: 子节点坐标
        parentPt: 父节点坐标
        txtString: 要添加的文本（特征值）
    """
    # 计算文本的x坐标（父子节点x坐标的中点）
    xMid = (parentPt[0] - cntrPt[0]) / 2.0 + cntrPt[0]
    # 计算文本的y坐标（父子节点y坐标的中点）
    yMid = (parentPt[1] - cntrPt[1]) / 2.0 + cntrPt[1]
    # 在计算出的坐标位置添加文本
    createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", color='red')

def plotTree(myTree, parentPt, nodeTxt):
    """
    函数功能：递归绘制整个决策树。
    参数：
        myTree: 要绘制的（子）树
        parentPt: 父节点坐标
        nodeTxt: 父节点到当前节点连线上的文本
    """
    # 定义决策节点和叶子节点的样式
    decisionNode = dict(boxstyle="sawtooth", fc="0.8") # 锯齿形方框
    leafNode = dict(boxstyle="round4", fc="0.8")       # 圆角方框
    # 获取当前树的叶子节点数和深度
    numLeafs = getNumLeafs(myTree)
    depth = getTreeDepth(myTree)
    # 获取当前树的根节点标签
    firstStr = next(iter(myTree))
    # 计算当前根节点的x坐标（根据子树的宽度平分）
    cntrPt = (plotTree.xOff + (1.0 + float(numLeafs)) / 2.0 / plotTree.totalW, plotTree.yOff)
    # 绘制父节点到当前根节点的连线，并标注文本
    plotMidText(cntrPt, parentPt, nodeTxt)
    # 绘制当前根节点（决策节点）
    plotNode(firstStr, cntrPt, parentPt, decisionNode)
    # 获取当前根节点的子树字典
    secondDict = myTree[firstStr]
    # 计算下一层节点的y坐标（向下移动）
    plotTree.yOff = plotTree.yOff - 1.0 / plotTree.totalD
    # 遍历子树的每个分支
    for key in secondDict.keys():
        # 如果分支是子树，则递归调用plotTree
        if type(secondDict[key]).__name__ == 'dict':
            plotTree(secondDict[key], cntrPt, str(key))
        else: # 如果分支是叶子节点
            # 计算下一个叶子节点的x坐标（向右移动）
            plotTree.xOff = plotTree.xOff + 1.0 / plotTree.totalW
            # 绘制叶子节点
            plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
            # 绘制父节点到叶子节点的连线，并标注特征值
            plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
    # 递归返回后，恢复y坐标（回到上一层）
    plotTree.yOff = plotTree.yOff + 1.0 / plotTree.totalD

def createPlot(inTree):
    """
    函数功能：创建绘图区域，并调用plotTree开始绘制决策树。
    参数：
        inTree: 已经构建好的决策树
    """
    # 创建一个图形
    fig = plt.figure(1, facecolor='white')
    # 清空图形
    fig.clf()
    # 定义坐标轴属性（无刻度）
    axprops = dict(xticks=[], yticks=[])
    # 创建一个子图，并设置为无边框
    createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)
    # 将全局变量totalW和totalD设置为树的宽度和深度，用于计算坐标
    plotTree.totalW = float(getNumLeafs(inTree))
    plotTree.totalD = float(getTreeDepth(inTree))
    # 初始化x和y的偏移量
    plotTree.xOff = -0.5 / plotTree.totalW
    plotTree.yOff = 1.0
    # 调用plotTree函数开始递归绘制
    plotTree(inTree, (0.5, 1.0), '') # 从(0.5, 1.0)开始，初始文本为空
    # 显示图形
    plt.show()

# ==================== 主程序 ====================

# 当该脚本作为主程序运行时，执行以下代码
if __name__ == '__main__':
    # 1. 创建数据集
    myDat, labels = createDataSet()
    
    # 2. 创建决策树
    # 创建一个空列表，用于存储决策树构建过程中实际使用的特征标签
    featLabels = []
    # 调用createTree函数，传入数据集、标签的副本（防止原标签被修改）和featLabels
    myTree = createTree(myDat, labels[:], featLabels)
    
    # 打印生成的决策树结构（字典形式）
    print("生成的决策树结构为:")
    print(myTree)
    
    # 3. 绘制决策树
    createPlot(myTree)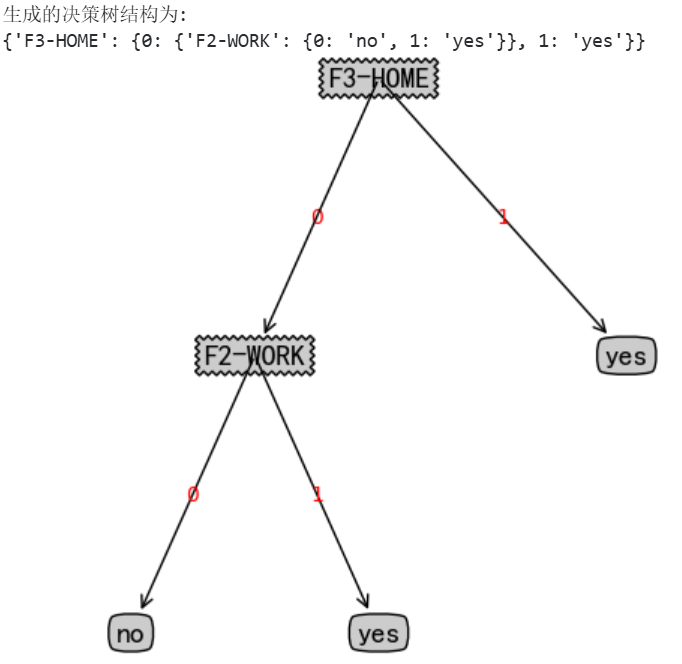

7.2 决策树模型可视化

下载graphviz，然后配置环境变量C:\Program Files\Graphviz\bin，最后打开终端，输入命令检测是否安装成功。
bash 复制代码
```
dot -version
```

如果输出类似的信息，即可说明安装成功。

bash 复制代码

C:\Users\yuan>dot -version
dot - graphviz version 12.2.1 (20241206.2353)
libdir = "C:\Program Files\Graphviz\bin"
Activated plugin library: gvplugin_dot_layout.dll
Using layout: dot:dot_layout

安装缺失的依赖
bash 复制代码
```
pip install scikit-learn
```

编辑运行代码

python 复制代码

import numpy as np
import os

# 设置 matplotlib 内联显示
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt

# 配置绘图参数
plt.rcParams['axes.labelsize'] = 14
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12

import warnings
warnings.filterwarnings('ignore')

from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier

iris = load_iris()
X = iris.data[:, 2:]  # petal length and width
y = iris.target
tree_clf = DecisionTreeClassifier(max_depth=2)
tree_clf.fit(X, y)

from sklearn. tree import export_graphviz

export_graphviz(
    tree_clf,
    out_file="iris_tree. dot",
    feature_names=iris.feature_names[2:],
    class_names=iris.target_names,
    rounded=True,
    filled=True
)

将dot文件转化为图片
bash 复制代码
```
dot -T png iris_tree.dot -o iris_tree.png
```

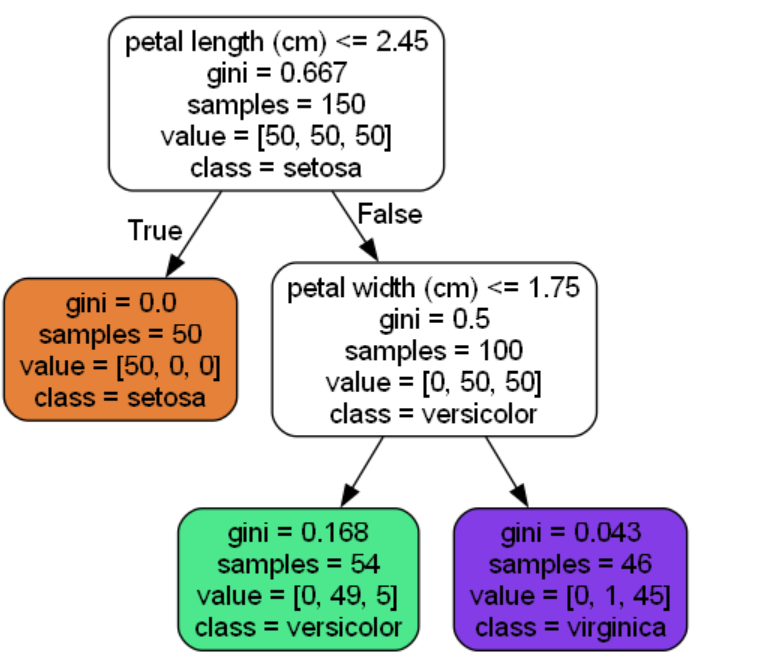
7.3 决策边界可视化

python 复制代码

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap

def plot_decision_boundary(clf, X, y, axes=[0, 7.5, 0, 3], iris=True, legend=False, plot_training=True):
    # 生成网格点用于预测
    x1s = np.linspace(axes[0], axes[1], 100)
    x2s = np.linspace(axes[2], axes[3], 100)
    x1, x2 = np.meshgrid(x1s, x2s)
    X_new = np.c_[x1.ravel(), x2.ravel()]
    
    # 预测网格点的类别并 reshape 为原网格形状
    y_pred = clf.predict(X_new).reshape(x1.shape)
    
    # 定义自定义颜色映射（用于填充区域）
    custom_cmap = ListedColormap(['#fafab0', '#9898ff', '#a0faa0'])
    plt.contourf(x1, x2, y_pred, alpha=0.3, cmap=custom_cmap)
    
    # 若非 Iris 数据集，绘制轮廓线（更清晰的边界）
    if not iris:
        custom_cmap2 = ListedColormap(['#7d7d58', '#4c4c7f', '#507d50'])
        plt.contour(x1, x2, y_pred, cmap=custom_cmap2, alpha=0.8)
    
    # 绘制训练数据点（若 plot_training 为 True）
    if plot_training:
        plt.plot(X[:, 0][y==0], X[:, 1][y==0], "yo", label="Iris-Setosa")
        plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs", label="Iris-Versicolor")
        plt.plot(X[:, 0][y==2], X[:, 1][y==2], "g^", label="Iris-Virginica")
    
    # 设置坐标轴范围
    plt.axis(axes)
    
    # 设置标签（根据 iris 参数区分数据集）
    if iris:
        plt.xlabel("Petal length", fontsize=14)
        plt.ylabel("Petal width", fontsize=14)
    else:
        plt.xlabel(r"$x_1$", fontsize=18)
        plt.ylabel(r"$x_2$", fontsize=18, rotation=0)
    
    # 添加图例（若 legend 为 True）
    if legend:
        plt.legend(loc="lower right", fontsize=14)

# 主程序：创建决策树模型并绘制边界
if __name__ == "__main__":
    # 加载 Iris 数据集（需先安装 scikit-learn：pip install scikit-learn）
    from sklearn.datasets import load_iris
    from sklearn.tree import DecisionTreeClassifier
    
    iris = load_iris()
    X = iris.data[:, 2:]  # 仅使用花瓣长度和宽度（第 2、3 列）
    y = iris.target
    
    # 训练决策树模型（未设置 max_depth，即完全生长）
    tree_clf = DecisionTreeClassifier(random_state=42)
    tree_clf.fit(X, y)
    
    # 创建图形并设置大小
    plt.figure(figsize=(8, 4))
    
    # 调用函数绘制决策边界
    plot_decision_boundary(tree_clf, X, y)
    
    # 绘制决策树的分割线（手动标注深度）
    plt.plot([2.45, 2.45], [0, 3], "k-", linewidth=2)          # Depth=0 分割线
    plt.plot([2.45, 7.5], [1.75, 1.75], "k--", linewidth=2)    # Depth=1 分割线
    plt.plot([4.95, 4.95], [0, 1.75], "k:", linewidth=2)       # Depth=2 分割线
    plt.plot([4.85, 4.85], [1.75, 3], "k:", linewidth=2)       # Depth=2 分割线
    
    # 添加深度标注
    plt.text(1.40, 1.0, "Depth=0", fontsize=15)
    plt.text(3.2, 1.80, "Depth=1", fontsize=13)
    plt.text(4.05, 0.5, "(Depth=2)", fontsize=11)
    
    # 设置标题并显示图形
    plt.title('Decision Tree decision boundaries')
    plt.show()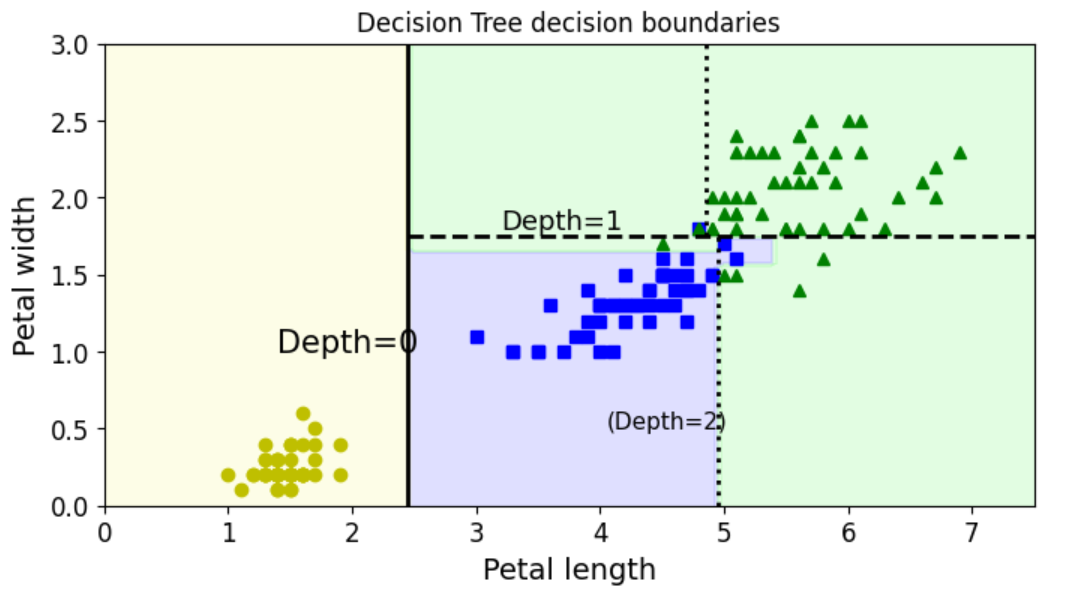

7.4 决策树的正则化（剪枝）

DecisionTreeClassifier 类中用于限制决策树复杂度的关键参数。这些参数通过约束树的形状（如节点数量、深度、样本分配等），防止模型过拟合（Overfitting），从而提高泛化能力。

DecisionTreeClassifier类的参数

min_samples_split：节点在分割之前必须具有的最小样本数
min_samples_leaf：叶子节点必须具有的最小样本数
max_leaf_nodes：叶子节点的最大数量
max_features：在每个节点处评估用于拆分的最大特征数
max_depth：树最大的深度

min_samples_split（节点分裂的最小样本数）

含义：指定一个内部节点（非叶子节点）在分裂成子节点之前，必须包含的最小样本数量。
作用：如果节点的样本数小于该值，则停止分裂，将该节点设为叶子节点。
示例：若 min_samples_split=10，则只有当节点包含至少 10 个样本时，才允许进一步分裂。
影响：值越大，树越简单（分裂次数减少）；值越小，树越复杂（容易过拟合）。

min_samples_leaf（叶子节点的最小样本数）

含义：指定每个叶子节点必须包含的最小样本数量。
作用：如果一个分裂操作会导致某个子节点的样本数小于该值，则该分裂会被禁止。
示例：若 min_samples_leaf=5，则任何叶子节点都不能少于 5 个样本。
影响：值越大，树越简单（叶子节点更"大"）；值越小，树越复杂（叶子节点更"细"）。

max_leaf_nodes（叶子节点的最大数量）

含义：限制决策树中叶子节点的总数。
作用：当达到指定的叶子节点数量时，停止分裂（即使还有节点满足分裂条件）。
示例：若 max_leaf_nodes=10，则树最多有 10 个叶子节点。
影响：值越小，树越简单；值越大，树越复杂（但不超过该上限）。

max_features（每个节点评估的最大特征数）

含义：在每个节点分裂时，随机选择的最大特征数量（用于寻找最佳分裂点）。
作用：限制每个节点考虑的特征范围，增加模型的随机性（类似随机森林的思想）。
示例：若 max_features='sqrt'，则每个节点只考虑 √(总特征数) 个特征；若 max_features=0.8，则考虑 80% 的特征。
影响：值越小，树越简单（特征选择受限）；值越大，树越复杂（更接近全特征分裂）。

max_depth（树的最大深度）

含义：限制决策树从根节点到叶子节点的最长路径长度（层数）。
作用：当达到指定深度时，停止分裂（即使节点仍满足分裂条件）。
示例：若 max_depth=3，则树最多有 3 层（根节点为第 0 层，叶子节点为第 3 层）。
影响：值越小，树越简单（浅树）；值越大，树越复杂（深树，易过拟合）。

这些参数都是正则化手段 ，目的是通过限制决策树的复杂度，平衡偏差（Bias）和方差（Variance）：

过深的树（高方差）：容易记住训练数据的噪声，泛化能力差（过拟合）。
过浅的树（高偏差）：无法捕捉数据中的复杂模式，泛化能力也差（欠拟合）。

通过调整这些参数，可以找到最优的树结构 ，使模型在训练数据和 unseen 数据上的表现都较好。例如，对于小数据集，可能需要设置较大的 min_samples_split 或较小的 max_depth；对于大数据集，可以适当放宽限制，但仍需通过交叉验证（Cross-Validation）确定最佳参数。

python 复制代码

from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, noise=0.25, random_state=53)
tree_clf1 = DecisionTreeClassifier(random_state=42)
tree_clf2 = DecisionTreeClassifier(min_samples_leaf=4, random_state=42)
tree_clf1.fit(X,y)
tree_clf2.fit(X,y)
plt.figure(figsize=(12,4))

plt.subplot(121)
plot_decision_boundary(tree_clf1, X, y, axes=[-1.5, 2.5, -1, 1.5])

plt.subplot(122)
plot_decision_boundary(tree_clf2, X, y, axes=[-1.5, 2.5, -1, 1.5])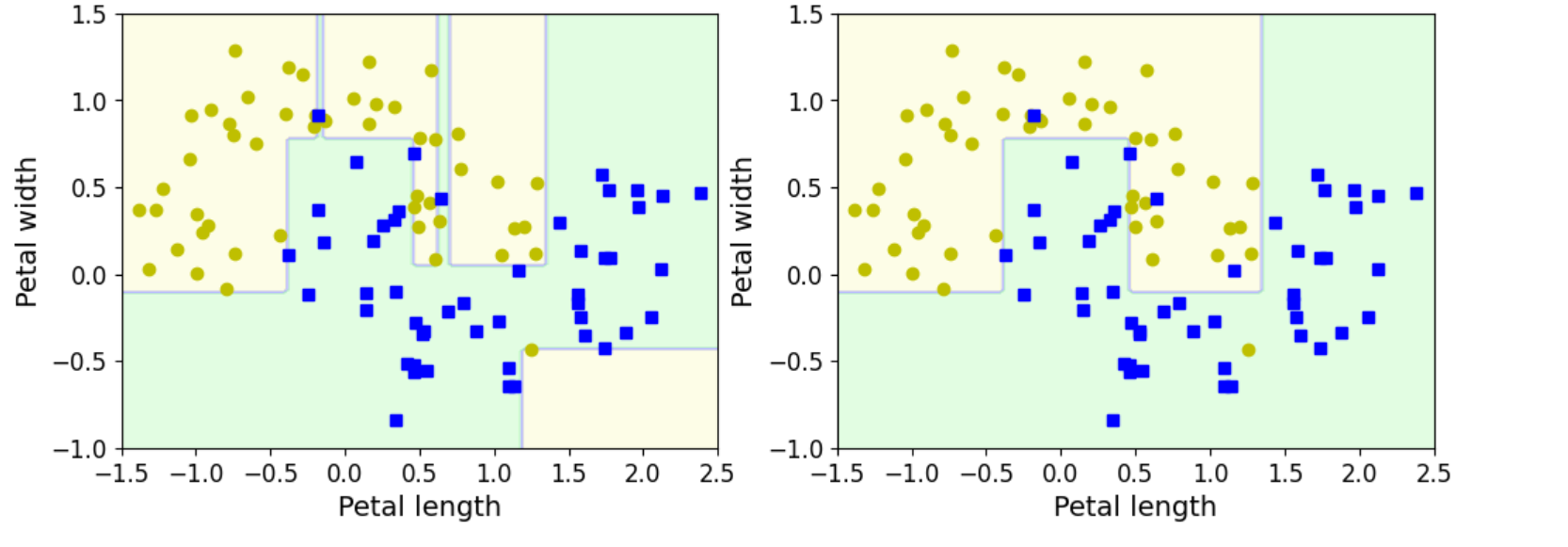

7.5 决策树模型的不稳定性

演示决策树对训练集旋转的敏感性：即使数据只是做了线性变换，决策树的决策边界也可能发生显著变化，反映了其不稳定性。

python 复制代码

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn.tree import DecisionTreeClassifier

# 固定随机种子以确保结果可复现
np.random.seed(6)

# 生成合成数据集
Xs = np.random.rand(100, 2) - 0.5  # 100个样本，2个特征，范围[-0.5, 0.5]
ys = (Xs[:, 0] > 0).astype(np.float32) * 2  # 标签：Xs[:,0]>0时为2，否则为0

# 对数据进行旋转（绕原点逆时针旋转π/4弧度）
angle = np.pi / 4
rotation_matrix = np.array([
    [np.cos(angle), -np.sin(angle)],
    [np.sin(angle), np.cos(angle)]
])
Xsr = Xs.dot(rotation_matrix)  # 应用旋转矩阵

# 训练两个决策树模型（相同参数，不同数据）
tree_clf_s = DecisionTreeClassifier(random_state=42)
tree_clf_s.fit(Xs, ys)

tree_clf_sr = DecisionTreeClassifier(random_state=42)
tree_clf_sr.fit(Xsr, ys)

# 绘制决策边界
plt.figure(figsize=(11, 4))

# 左侧子图：原始数据
plt.subplot(121)
plot_decision_boundary(tree_clf_s, Xs, ys, 
                      axes=[-0.7, 0.7, -0.7, 0.7], 
                      iris=False)
plt.title('Sensitivity to training set rotation')

# 右侧子图：旋转后的数据
plt.subplot(122)
plot_decision_boundary(tree_clf_sr, Xsr, ys, 
                      axes=[-0.7, 0.7, -0.7, 0.7], 
                      iris=False)
plt.title('Sensitivity to training set rotation')

plt.tight_layout()  # 自动调整子图间距
plt.show()

以下是整理后的完整代码，包含了必要的导入语句和修正后的细节（如 random.seed 改为 np.random.seed 以确保一致性）：

python 复制代码

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn.tree import DecisionTreeClassifier
# 固定随机种子以确保结果可复现
np.random.seed(6)
# 生成合成数据集
Xs = np.random.rand(100, 2) - 0.5  # 100个样本，2个特征，范围[-0.5, 0.5]
ys = (Xs[:, 0] > 0).astype(np.float32) * 2  # 标签：Xs[:,0]>0时为2，否则为0
# 对数据进行旋转（绕原点逆时针旋转π/4弧度）
angle = np.pi / 4
rotation_matrix = np.array([
    [np.cos(angle), -np.sin(angle)],
    [np.sin(angle), np.cos(angle)]
])
Xsr = Xs.dot(rotation_matrix)  # 应用旋转矩阵
# 训练两个决策树模型（相同参数，不同数据）
tree_clf_s = DecisionTreeClassifier(random_state=42)
tree_clf_s.fit(Xs, ys)
tree_clf_sr = DecisionTreeClassifier(random_state=42)
tree_clf_sr.fit(Xsr, ys)
# 绘制决策边界
plt.figure(figsize=(11, 4))
# 左侧子图：原始数据
plt.subplot(121)
plot_decision_boundary(tree_clf_s, Xs, ys, 
                      axes=[-0.7, 0.7, -0.7, 0.7], 
                      iris=False)
plt.title('Sensitivity to training set rotation')
# 右侧子图：旋转后的数据
plt.subplot(122)
plot_decision_boundary(tree_clf_sr, Xsr, ys, 
                      axes=[-0.7, 0.7, -0.7, 0.7], 
                      iris=False)
plt.title('Sensitivity to training set rotation')
plt.tight_layout()  # 自动调整子图间距
plt.show()

数据生成 ：使用 np.random.rand(100, 2) 生成 100 个二维随机样本（范围 [0,1)），减去 0.5 使范围变为 [-0.5, 0.5)。标签 ys 基于第一个特征 Xs[:,0]：若大于 0 则标记为 2，否则为 0（二分类任务）。
数据旋转：通过旋转矩阵（角度 π/4）对数据进行了线性变换，模拟"训练集旋转"的场景。
模型训练 ：两个决策树模型使用相同的随机状态（random_state=42），确保唯一差异是输入数据（原始 vs 旋转后）。
决策边界绘制 ：使用 plot_decision_boundary 函数（需提前定义，见之前的代码片段）绘制两个模型的决策边界。子图布局为 1 行 2 列（121 和 122），便于对比原始数据和旋转后数据的决策边界变化。
可视化优化 ：使用 plt.tight_layout() 自动调整子图间距，避免标题重叠。坐标轴范围统一为 [-0.7, 0.7]。

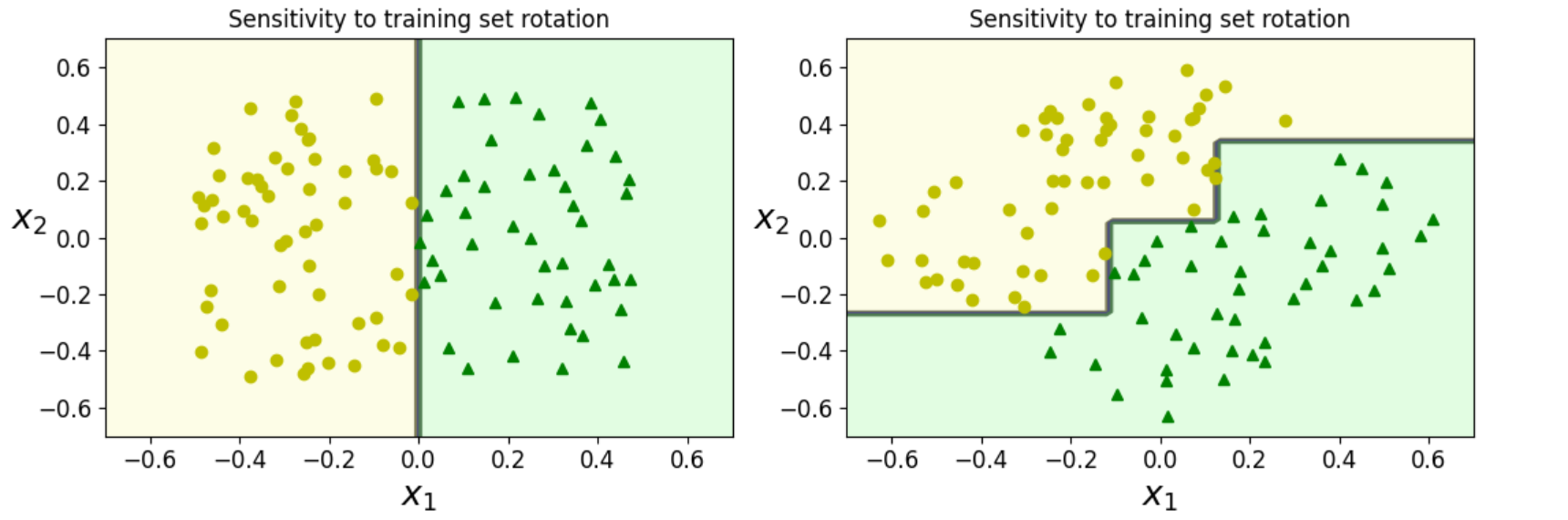
八回归树模型(决策树用于回归任务)

8.1 决策树模型创建和绘制

python 复制代码

import numpy as np
from sklearn.tree import DecisionTreeRegressor, export_graphviz

# 固定随机种子以确保结果可复现
np.random.seed(42)

# 生成合成回归数据集
m = 200  # 样本数量
X = np.random.rand(m, 1)  # 200个样本，1个特征（范围[0,1)）
y = 4 * (X - 0.5) ** 2  # 基础二次函数关系
y = y + np.random.randn(m, 1) / 10  # 添加高斯噪声（均值为0，标准差0.1）

# 训练决策树回归模型（限制最大深度为2）
tree_reg = DecisionTreeRegressor(max_depth=2, random_state=42)
tree_reg.fit(X, y)

# 导出决策树为Graphviz格式文件
export_graphviz(
    tree_reg,
    out_file="regression_tree.dot",
    feature_names=["x1"],
    rounded=True,
    filled=True
)

# dot -T png regression_tree.dot -o regression_tree.png

# 图画展示
from IPython.display import Image
Image(filename="regression_tree.png", width=600, height=600)

bash 复制代码

dot -T png regression_tree.dot -o regression_tree.png

8.2 不同深度切分可视化

python 复制代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor

# 固定随机种子以确保结果可复现
np.random.seed(42)

# 1. 生成合成回归数据集
m = 200  # 样本数量
X = np.random.rand(m, 1)  # 200个样本，1个特征（范围[0,1)）
y = 4 * (X - 0.5) ** 2  # 基础二次函数关系
y = y + np.random.randn(m, 1) / 10  # 添加高斯噪声（均值为0，标准差0.1）

# 2. 训练两个决策树回归模型（不同最大深度）
tree_reg1 = DecisionTreeRegressor(random_state=42, max_depth=2)
tree_reg1.fit(X, y)

tree_reg2 = DecisionTreeRegressor(random_state=42, max_depth=3)
tree_reg2.fit(X, y)

# 3. 定义一个辅助函数，用于递归获取树的切分点信息
def get_tree_splits(tree, feature_names=None):
    """
    递归遍历决策树，收集所有切分点的信息。
    返回一个列表，每个元素是一个元组: (深度, 特征索引, 阈值)
    """
    tree_ = tree.tree_
    splits_info = []

    def recurse(node_id, depth):
        # 如果当前节点是叶子节点，则停止
        if tree_.feature[node_id] != -2:  # -2 表示叶子节点
            feature = tree_.feature[node_id]
            threshold = tree_.threshold[node_id]
            
            # 记录当前切分点的信息
            splits_info.append((depth, feature, threshold))
            
            # 递归遍历左子树和右子树
            recurse(tree_.children_left[node_id], depth + 1)
            recurse(tree_.children_right[node_id], depth + 1)

    # 从根节点（ID为0）开始遍历
    recurse(0, 0)
    return splits_info

# 4. 定义绘制回归预测结果的函数（已完善切分线绘制逻辑）
def plot_regression_predictions(tree_reg, X, y, axes=[0, 1, -0.2, 1], ylabel="$y$"):
    """
    绘制决策树的回归预测结果和切分线。
    """
    # 生成用于绘制平滑曲线的测试数据
    x1 = np.linspace(axes[0], axes[1], 500).reshape(-1, 1)
    y_pred = tree_reg.predict(x1)
    
    # 绘制原始数据点
    plt.plot(X[:, 0], y, "b.")
    # 绘制模型的预测曲线
    plt.plot(x1, y_pred, "r.-", linewidth=2, label=r"$\hat{y}$")
    
    # --- 完善的切分线绘制逻辑 ---
    splits = get_tree_splits(tree_reg)
    for depth, feature, threshold in splits:
        # 只绘制与x1轴（特征0）相关的切分线
        if feature == 0:
            # 根据深度设置线条样式，使其更清晰
            # 深度0（根节点）：实线，较粗
            # 深度1：虚线
            # 深度2：点划线
            linestyle = '-' if depth == 0 else '--' if depth == 1 else '-.'
            plt.axvline(x=threshold, color='k', linestyle=linestyle, alpha=0.7)
            
            # 在图的顶部添加切分点的标注
            plt.text(threshold, axes[3] * 0.95, f"Depth={depth}", 
                     horizontalalignment='center', color='k', fontsize=9)

    plt.axis(axes)
    plt.xlabel("$x_1$", fontsize=18)
    plt.ylabel(ylabel, fontsize=18, rotation=0, labelpad=10)
    plt.legend(loc="upper center", fontsize=16)

# 5. 创建并绘制两个子图
plt.figure(figsize=(12, 6))

# 左侧子图：max_depth=2
plt.subplot(121)
plot_regression_predictions(tree_reg1, X, y)
plt.title("max_depth=2", fontsize=14)

# 右侧子图：max_depth=3
plt.subplot(122)
plot_regression_predictions(tree_reg2, X, y)
plt.title("max_depth=3", fontsize=14)

plt.show()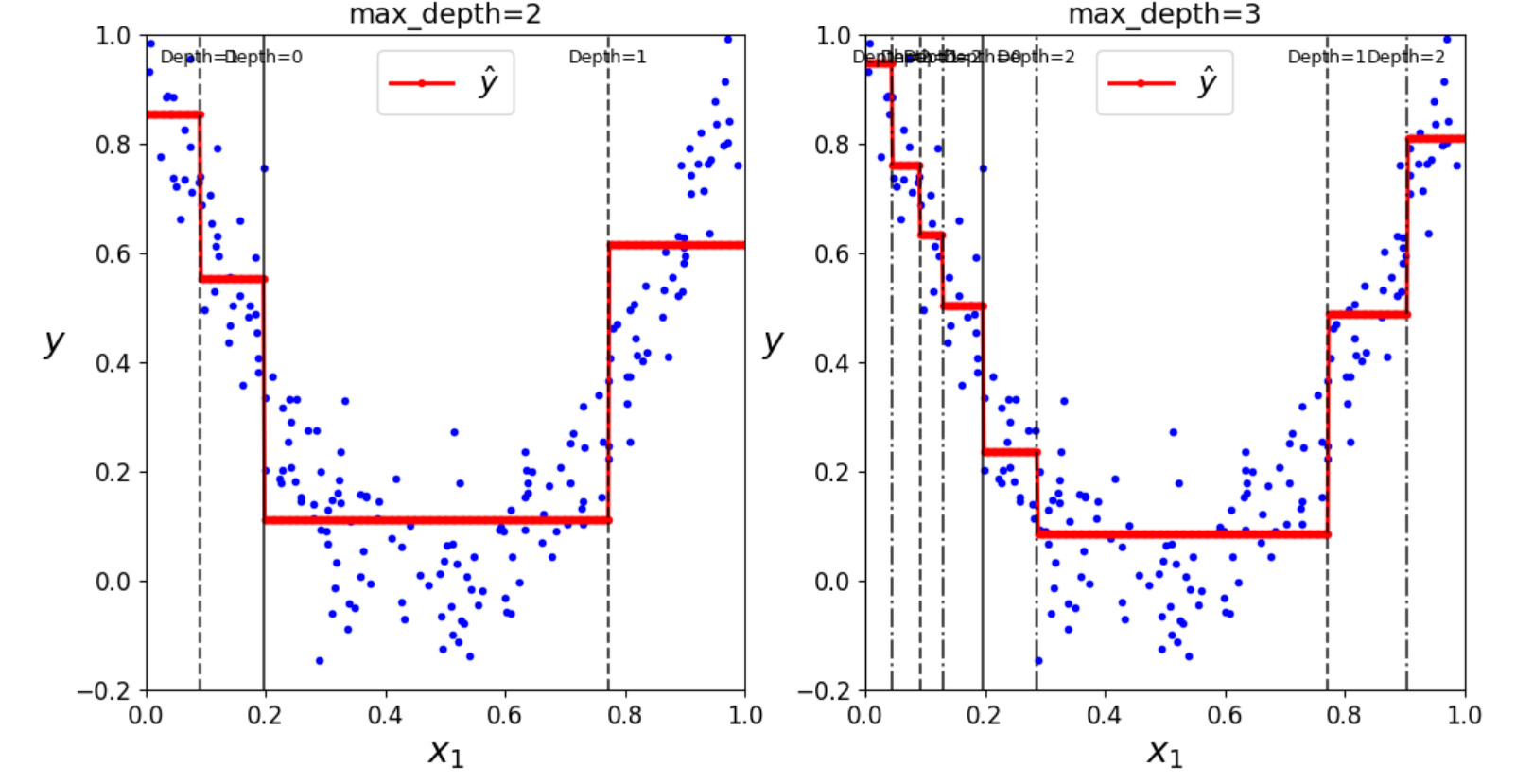

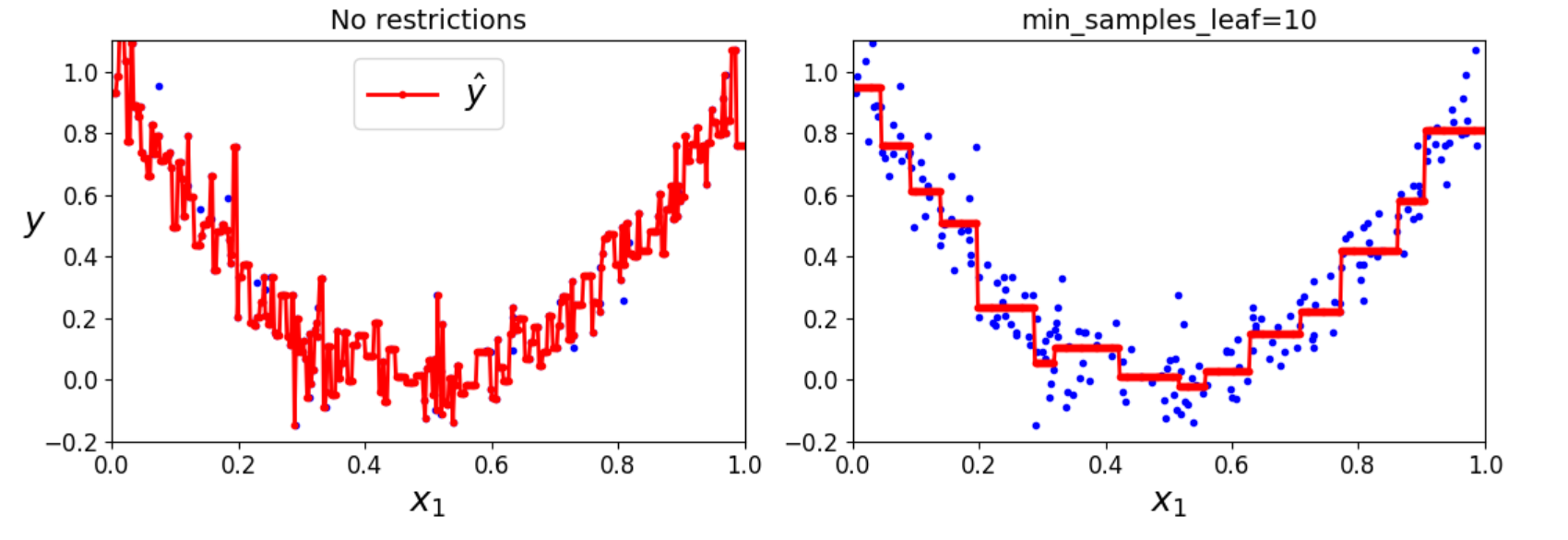
8.3 设置最小叶子节点数效果

python 复制代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor

# 固定随机种子以确保结果可复现
np.random.seed(42)

# 生成合成回归数据集（与之前一致）
m = 200  # 样本数量
X = np.random.rand(m, 1)  # 200个样本，1个特征（范围[0,1)）
y = 4 * (X - 0.5) ** 2  # 基础二次函数关系
y = y + np.random.randn(m, 1) / 10  # 添加高斯噪声（均值为0，标准差0.1）

# 训练两个决策树回归模型（不同正则化参数）
tree_reg1 = DecisionTreeRegressor(random_state=42)  # 无限制
tree_reg1.fit(X, y)

tree_reg2 = DecisionTreeRegressor(random_state=42, min_samples_leaf=10)  # 叶子节点最小样本数为10
tree_reg2.fit(X, y)

# 生成测试点以绘制平滑曲线
x1 = np.linspace(0, 1, 500).reshape(-1, 1)
y_pred1 = tree_reg1.predict(x1)
y_pred2 = tree_reg2.predict(x1)

# 创建图形并设置大小
plt.figure(figsize=(11, 4))

# 左侧子图：无限制的决策树
plt.subplot(121)
plt.plot(X, y, "b.")  # 实际数据点
plt.plot(x1, y_pred1, "r.-", linewidth=2, label=r"$\hat{y}$")  # 预测曲线
plt.axis([0, 1, -0.2, 1.1])  # 坐标轴范围
plt.xlabel("$x_1$", fontsize=18)  # x轴标签
plt.ylabel("$y$", fontsize=18, rotation=0)  # y轴标签
plt.legend(loc="upper center", fontsize=18)  # 图例位置
plt.title("No restrictions", fontsize=14)  # 标题

# 右侧子图：限制 min_samples_leaf 的决策树
plt.subplot(122)
plt.plot(X, y, "b.")  # 实际数据点
plt.plot(x1, y_pred2, "r.-", linewidth=2, label=r"$\hat{y}$")  # 预测曲线
plt.axis([0, 1, -0.2, 1.1])  # 坐标轴范围
plt.xlabel("$x_1$", fontsize=18)  # x轴标签
plt.title(f"min_samples_leaf={tree_reg2.min_samples_leaf}", fontsize=14)  # 动态标题（显示参数值）

# 显示图形
plt.tight_layout()
plt.show()

机器学习中的决策树

文章目录

一 树模型

二 决策树的训练与测试

2.1 核心问题

2.2 核心目标

2.3 关键衡量逻辑

三 衡量标准

3.1 熵的定义

3.2 熵的计算公式

3.3 实例验证（A集合 vs B集合）

3.4 熵在决策树分类任务中的作用

四 决策树构造实例

五 决策树算法

5.1 ID3 算法

5.2 C4.5 算法

5.3 CART 算法

六 决策树剪枝策略

6.1 为什么要剪枝？------ 过拟合风险的根源

6.2 剪枝策略的分类：预剪枝 vs 后剪枝

6.2.1 预剪枝（Pre - pruning）：生长过程中主动限制

6.2.2 后剪枝（Post - pruning）：生长完成后被动修剪

6.3 预剪枝与后剪枝的工程选择逻辑

七 决策树代码实现和可视化

7.1 决策树代码实现

7.2 决策树模型可视化

7.3 决策边界可视化

7.4 决策树的正则化（剪枝）

7.5 决策树模型的不稳定性

八 回归树模型(决策树用于回归任务)

8.1 决策树模型创建和绘制

8.2 不同深度切分可视化

8.3 设置最小叶子节点数效果

一树模型

二决策树的训练与测试

三衡量标准

四决策树构造实例

五决策树算法

六决策树剪枝策略

七决策树代码实现和可视化

八回归树模型(决策树用于回归任务)