【剑斩OFFER】算法的暴力美学——将 x 减到零的最小操作数

一、题目描述

二、算法原理

我们这道题的要求是找最小的次数的数组的和能刚到把 x 减为 0 ，直接按题目的要求来解题太困难了，我们可以运用一下反向思维，假设一个数组的长度位 4，和等于16，x = 5；那么 16 - 5 = 9，也就是说我们只要找到最长的子数组剩下的子数组就是题目要求的次数；例如：

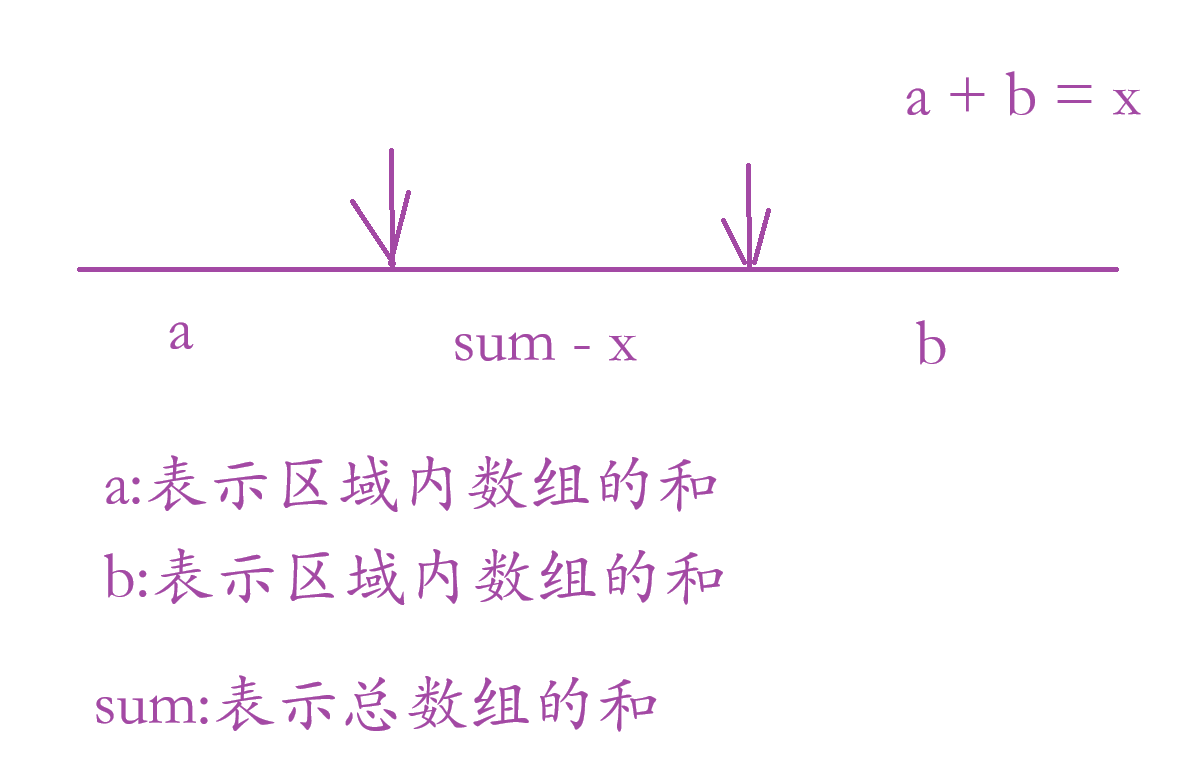
所以我们由上图可知只要求出 sum - x 的最长子数组就可以得出题目要求的最小操作数。

思路：使用滑动窗口来解决。

①我们先定义两个指针来指向第一个数，再定义 len 来找到最长的子数组，再定义 sum 来表示right 在右移动的加起来值

②right++过程中只要sum > target， sum -= nums $left$ ，left++；

③此时结果有两种：sum == target , sum < target ，只有 sum == target 才符合条件，所以才可以更新 len 的值。

模拟过程：

所以最终答案：数组的总长度 - len

三、代码实现

cpp 复制代码

class Solution {
public:
    int minOperations(vector<int>& nums, int x) {
        int right = 0, left = 0, sum = 0,target = 0;
        for(auto e : nums)
        {
            sum += e;
        }
        target = sum - x;
        if(target == 0) return nums.size();
        sum = 0;

        int len = -1;
        while(right < nums.size())
        {
            sum += nums[right];
            while(left < nums.size() && sum > target) sum -= nums[left++];
            if(sum == target) len = max(len,right - left + 1);
            right++;
        }
        if(len == -1) return len;
        else return nums.size() - len;
    }
};

探索性代码：

cpp 复制代码

class Solution {
public:
    int minOperations(vector<int>& nums, int x) {
        int right = 0, left = 0, sum = 0,target = 0;
        for(auto e : nums)
        {
            sum += e;
        }
        target = sum - x;
        if(target == 0) return nums.size();
        sum = 0;

        int len = 0;
        while(right < nums.size())
        {
            sum += nums[right];
            while(left < nums.size() && sum > target)
            {
                sum -= nums[left++];
            }
            if(sum == target) len = max(len,right - left + 1);
            right++;
        }
        return len == 0 ? -1 : nums.size() - len;
    }
};